Содержание
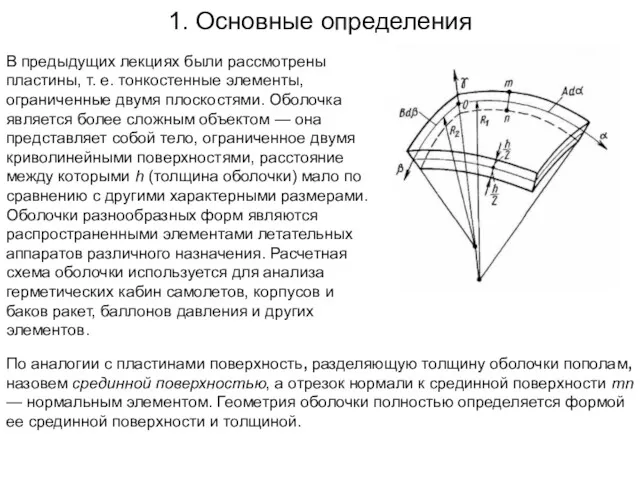
- 2. 1. Основные определения В предыдущих лекциях были рассмотрены пластины, т. е. тонкостенные элементы, ограниченные двумя плоскостями.
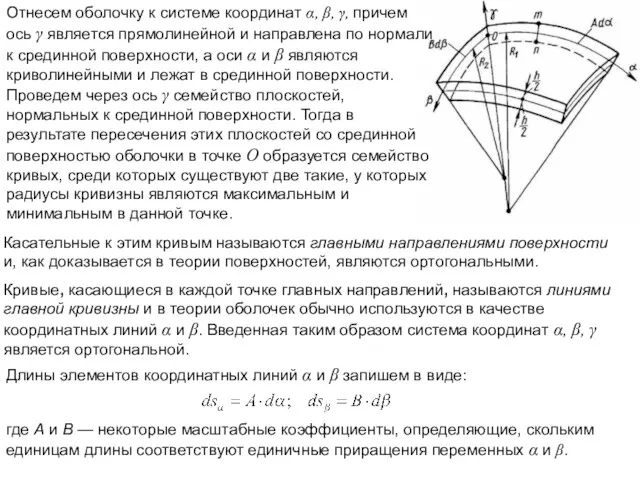
- 3. Отнесем оболочку к системе координат α, β, γ, причем ось γ является прямолинейной и направлена по
- 4. Тогда квадрат длины дуги произвольного элемента, лежащего в срединной поверхности, равен: Полученное соотношение называется первой квадратичной
- 5. Однако для оболочек небольшой кривизны, у которых радиусы кривизны существенно больше толщины оболочки дроби в скобках
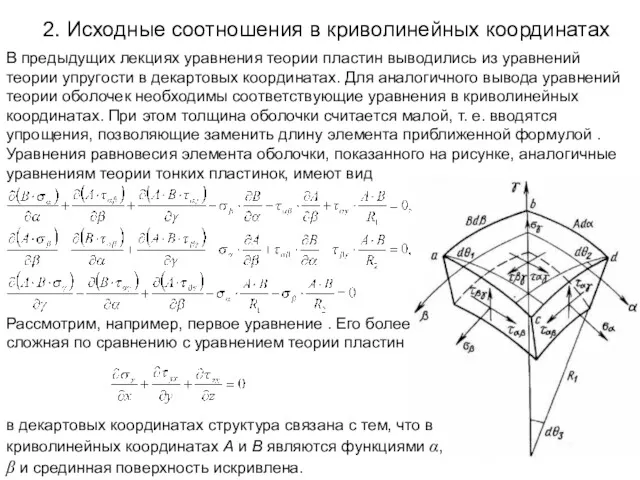
- 6. 2. Исходные соотношения в криволинейных координатах В предыдущих лекциях уравнения теории пластин выводились из уравнений теории
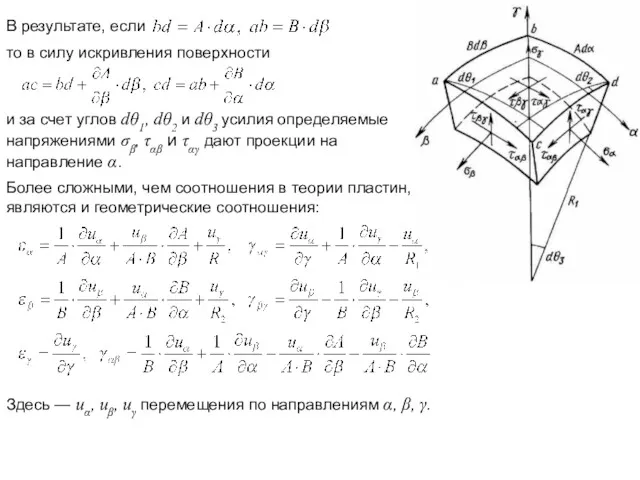
- 7. В результате, если то в силу искривления поверхности и за счет углов dθ1, dθ2 и dθ3
- 8. Физические соотношения выражают закон Гука и с точностью до обозначений совпадают с аналогичными уравнениями теории пластин
- 9. 3. Основные соотношения общей теории оболочек Теория оболочек, так же как и теория пластин, базируется на
- 10. -деформации удлинения и сдвига срединной поверхности; где - изменения кривизны и кручение срединной поверхности Подставляя полученные
- 11. В соответствии с гипотезами Кирхгофа в законе Гука следует пренебречь напряжениями σγ по сравнению с σα
- 12. По аналогии с теорией пластин вводим понятие погонных усилий и моментов. Учитывая связь погонных усилий и
- 13. Таким образом, в качестве основного элемента оболочки можно рассматривать элемент срединной поверхности, нагруженный усилиями и моментами,
- 14. Поставляя усилия в уравнения равновесия получим: где qα, qβ, qγ - поверхностные нагрузки, отнесенные к срединной
- 15. Согласно общей схеме решения задачи в перемещениях, система уравнений теории оболочек может быть сведена к трем
- 16. Если в результате решения данной системы найдены перемещения u(α,β), v(α,β), w(α,β), то далее по формулам основных
- 17. 4.Граничные условия Разрешающие уравнения общей теории оболочек имеют в совокупности восьмой порядок по переменным α и
- 18. Распространенным является так называемое скользящее шарнирное опирание (свободное опирание) края. Граничные условия при этом имеют вид:
- 19. 5. Полная энергия оболочки Потенциальная энергия тонкой оболочки небольшой кривизны, имеет вид, аналогичный теории пластин: Подставляя
- 20. 6. Осесимметричная деформация цилиндрической оболочки Рассмотрим достаточно простой и тем не менее важный для приложений пример
- 21. Геометрические соотношения типа в цилиндрических координатах для осесимметричной задачи преобразуются к виду: Две последних деформации равны
- 22. На основании гипотез Кирхгофа получим частную форму выражений для перемещений для рассматриваемого случая где w(α) и
- 23. здесь, как и ранее:
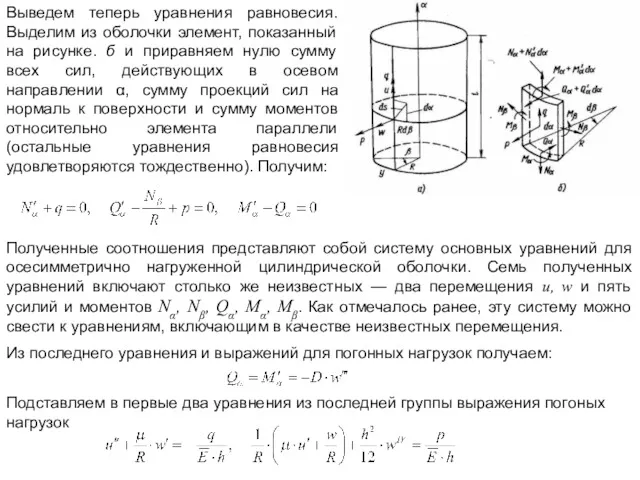
- 24. Выведем теперь уравнения равновесия. Выделим из оболочки элемент, показанный на рисунке. б и приравняем нулю сумму
- 25. Во многих случаях задача является статически определимой относительно усилий Να — они могут быть получены путем
- 26. Краевой эффект и безмоментное состояние Общее решение дифференциального уравнения запишем в виде: где w0(α) — частное
- 27. Если правая часть дифференциального уравнения представлена в виде полинома по степеням α с показателями, не превышающими
- 28. Краевой эффект возникает в том случае, когда на краю оболочка нагружается моментным образом (поперечными силами, моментами),
- 30. Скачать презентацию






















 Презентация по физике для 8 класса - своя игра по теме Электричество
Презентация по физике для 8 класса - своя игра по теме Электричество Полимерлер. Полимерлердің тұрлері
Полимерлер. Полимерлердің тұрлері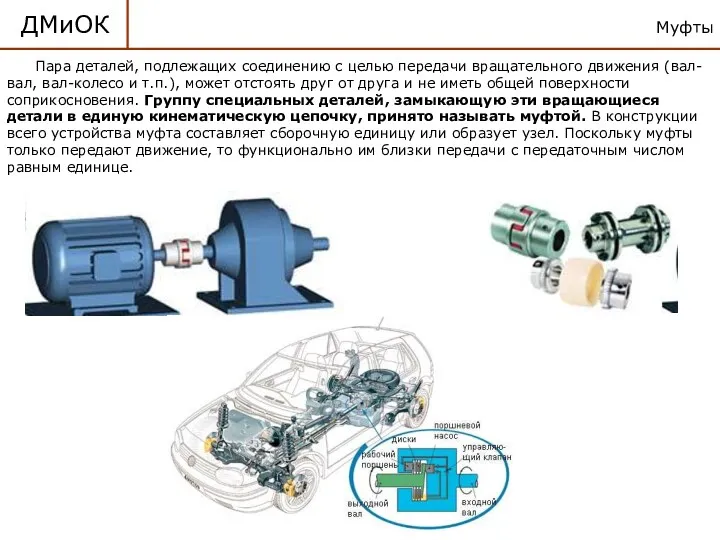 Детали машин и основы конструирования. Муфты. (Лекция 12)
Детали машин и основы конструирования. Муфты. (Лекция 12) Оптичні ілюзії
Оптичні ілюзії Плоская система сил. Центр параллельных сил (статика, лекция 6)
Плоская система сил. Центр параллельных сил (статика, лекция 6) Понятие симметрии и законы сохранения в природе
Понятие симметрии и законы сохранения в природе Молекулярная физика и термодинамика
Молекулярная физика и термодинамика Линейные электрические цепи постоянного тока. (Лекция 1)
Линейные электрические цепи постоянного тока. (Лекция 1) А.С. Попов – изобретатель радио
А.С. Попов – изобретатель радио Связанные уравнения для трехволновых процессов при высокой эффективности преобразования
Связанные уравнения для трехволновых процессов при высокой эффективности преобразования Изучение электрической цепи.
Изучение электрической цепи. Перемещения при изгибе
Перемещения при изгибе Функціональні системи вертольота Ми-2. Знімне обладнання вертольота
Функціональні системи вертольота Ми-2. Знімне обладнання вертольота Электростатика. Закон сохранения заряда
Электростатика. Закон сохранения заряда Энергия топлива. Удельная теплота сгорания топлива
Энергия топлива. Удельная теплота сгорания топлива Радиолокация. Радар
Радиолокация. Радар Метод наложения. Электрические цепи постоянного тока
Метод наложения. Электрические цепи постоянного тока Мұнай және газ механикасы
Мұнай және газ механикасы Работа, теплота, первое начало в термодинамике. (Лекция 6)
Работа, теплота, первое начало в термодинамике. (Лекция 6) Презентация к интегрированному уроку география -физика Северный Ледовитый океан 7 класс
Презентация к интегрированному уроку география -физика Северный Ледовитый океан 7 класс Электромагнитное ионизирующее излучение
Электромагнитное ионизирующее излучение Тема 6. Устойчивость САУ. Лекция 11. Критерий устойчивости Найквиста для статических и астатических САУ. Запас устойчивости
Тема 6. Устойчивость САУ. Лекция 11. Критерий устойчивости Найквиста для статических и астатических САУ. Запас устойчивости Хроматография. Основные виды хроматографии
Хроматография. Основные виды хроматографии Биологическое действие радиации
Биологическое действие радиации Электрические явления.
Электрические явления. Презентация к уроку на тему: Цепная Ядерная реакция
Презентация к уроку на тему: Цепная Ядерная реакция Сравнительный анализ бензиновых и дизельных двигателей
Сравнительный анализ бензиновых и дизельных двигателей Конспект урока. Сила упругости. Закон Гука
Конспект урока. Сила упругости. Закон Гука