Содержание
- 2. Уравнение упругой линии балки Существуют три метода решения дифференциального уравнения упругой линии балки. Это метод непосредственного
- 3. Уравнение упругой линии балки Метод Клебша Для составления уравнений необходимо выполнить следующие основные условия: начало координат,
- 4. Уравнение упругой линии балки Метод начальных параметров Для углов поворота: Для прогибов: Где θ—угол поворота сечения,
- 6. Скачать презентацию
Слайд 2
Уравнение упругой линии балки
Существуют три метода решения дифференциального уравнения упругой линии
Уравнение упругой линии балки
Существуют три метода решения дифференциального уравнения упругой линии
балки. Это метод непосредственного интегрирования, метод Клебша и метод начальных параметров.
Проинтегрировав уравнение упругой линии балки первый раз, получают выражение для определения углов поворота:
Интегрируя второй раз, находят выражения для определения прогибов:
Метод непосредственного интегрирования
Значения постоянных интегрирования С и D определяют из начальных условий на опорах балки
Слайд 3
Уравнение упругой линии балки
Метод Клебша
Для составления уравнений необходимо выполнить следующие основные
Уравнение упругой линии балки
Метод Клебша
Для составления уравнений необходимо выполнить следующие основные
условия:
начало координат, для всех участков, необходимо расположить в крайнем левом конце балки;
интегрирование дифференциального уравнения упругой линии балки проводить, не раскрывая скобок;
при включении в уравнение внешнего сосредоточенного момента М его необходимо помножить на (Z-a)0 где а - координата сечения, в котором приложен момент;
в случае обрыва распределенной нагрузки ее продлевают до конца балки, а для восстановления действительных условий нагружения вводят «компенсирующую» нагрузку обратного направления
начало координат, для всех участков, необходимо расположить в крайнем левом конце балки;
интегрирование дифференциального уравнения упругой линии балки проводить, не раскрывая скобок;
при включении в уравнение внешнего сосредоточенного момента М его необходимо помножить на (Z-a)0 где а - координата сечения, в котором приложен момент;
в случае обрыва распределенной нагрузки ее продлевают до конца балки, а для восстановления действительных условий нагружения вводят «компенсирующую» нагрузку обратного направления
Слайд 4
Уравнение упругой линии балки
Метод начальных параметров
Для углов поворота:
Для прогибов:
Где θ—угол поворота
Уравнение упругой линии балки
Метод начальных параметров
Для углов поворота:
Для прогибов:
Где θ—угол поворота
сечения, w—прогиб, θ0 - угол поворота в начале координат, w0—прогиб в начале координат, di—расстояние от начало координат до i-той опоры балки, ai—расстояние от начало координат до точки приложения сосредоточенного момента Mi , bi—расстояние от начало координат до точки приложения сосредоточенной силы Fi , сi—расстояние от начало координат до начала участка распределенной нагрузки qi , Ri и Мрi—реакция и реактивный момент в опорах балки.
Следующая -
Чернобыль. До и после


 Диагностика и ремонт тормозной системы легкового автомобиля
Диагностика и ремонт тормозной системы легкового автомобиля Вырожденные полупроводники
Вырожденные полупроводники Теплотехника. Основы теплопередачи
Теплотехника. Основы теплопередачи Химические источники тока
Химические источники тока Теория электрических цепей
Теория электрических цепей История создания швейной машинки
История создания швейной машинки Телескоп, принцип работы и его назначение
Телескоп, принцип работы и его назначение Принцип суперпозиции полей.Урок одной задачи
Принцип суперпозиции полей.Урок одной задачи КИМ ЕГЭ по физике в 2015 г
КИМ ЕГЭ по физике в 2015 г Úlohy merania mikroklímy
Úlohy merania mikroklímy Фізико-хімічна сутність процесу розчинення. Теплові явища, що супроводжують розчинення речовин
Фізико-хімічна сутність процесу розчинення. Теплові явища, що супроводжують розчинення речовин Явление отражения звука
Явление отражения звука 20191124_elektrichesk_tok
20191124_elektrichesk_tok Розчинник
Розчинник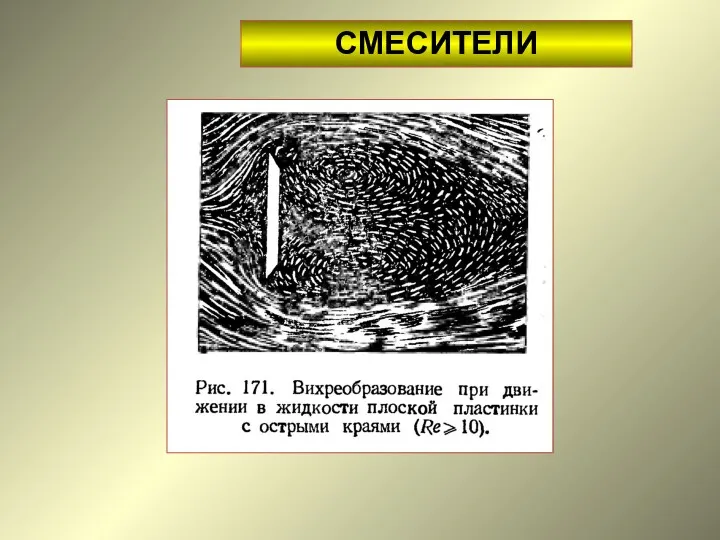 Смесители. Пропеллерная мешалка
Смесители. Пропеллерная мешалка Сложение сил. Равнодействующая сил. Физика. 7 класс
Сложение сил. Равнодействующая сил. Физика. 7 класс Визначення середнньої швидкості нерівномірного руху
Визначення середнньої швидкості нерівномірного руху Кинетика химических реакций. (Лекция 12)
Кинетика химических реакций. (Лекция 12) Электрические цепи постоянного тока
Электрические цепи постоянного тока Динамика механической системы и твердого тела(§9 - §11). Теорема об изменении момента количества движения системы
Динамика механической системы и твердого тела(§9 - §11). Теорема об изменении момента количества движения системы Действие произвольной возмущающей нагрузки
Действие произвольной возмущающей нагрузки Тепловое излучение
Тепловое излучение Решение задач на расчет количества теплоты. Урок физики в 8 классе
Решение задач на расчет количества теплоты. Урок физики в 8 классе Подготовка к контрольной работе №1
Подготовка к контрольной работе №1 Устройство мопеда
Устройство мопеда Урок - исследование. Воздух и его свойства. Воздушная оболочка Земли
Урок - исследование. Воздух и его свойства. Воздушная оболочка Земли Силы в природе
Силы в природе Давление твердых тел. Единицы давления
Давление твердых тел. Единицы давления