Содержание
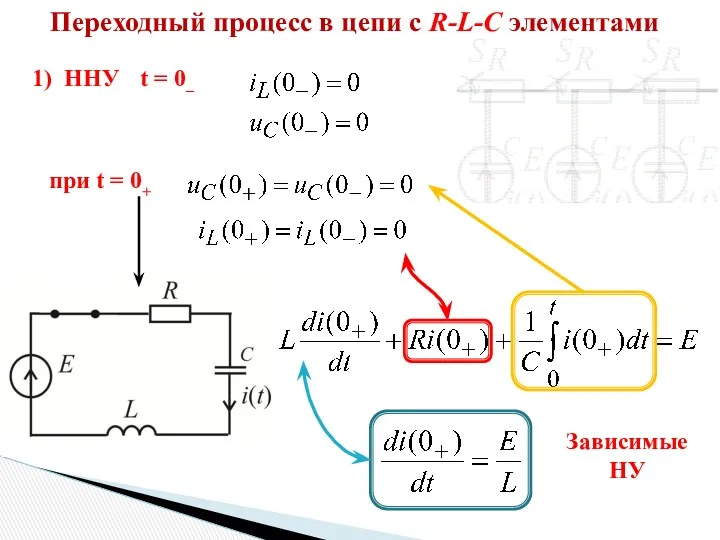
- 2. Переходный процесс в цепи с R-L-C элементами 1) ННУ t = 0– при t = 0+
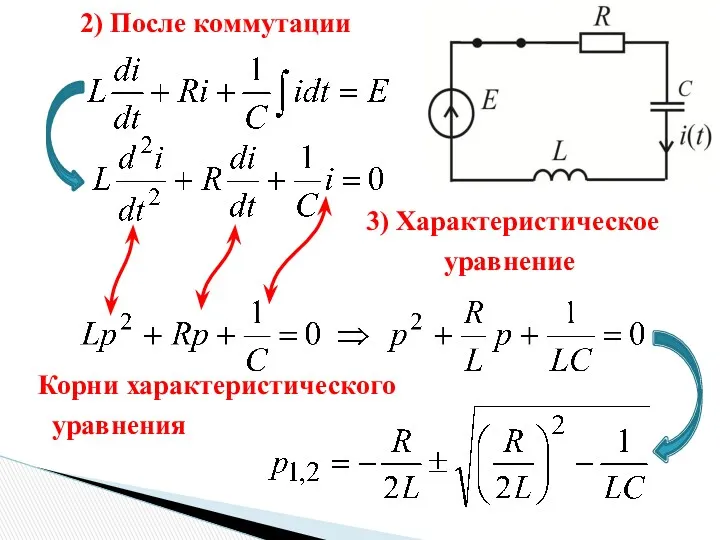
- 3. 2) После коммутации 3) Характеристическое уравнение Корни характеристического уравнения
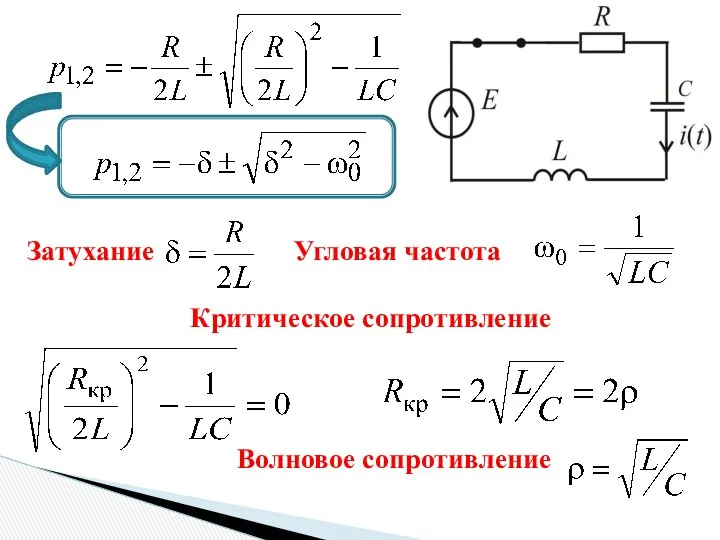
- 4. Затухание Угловая частота Критическое сопротивление Волновое сопротивление
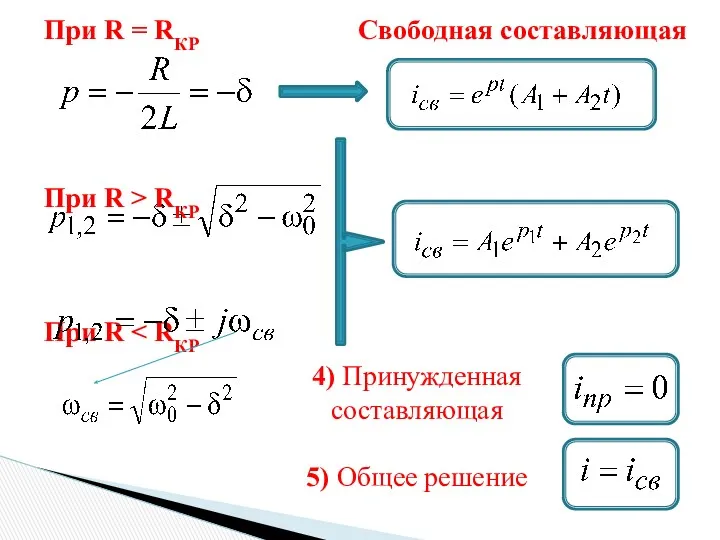
- 5. При R = RКР Свободная составляющая При R > RКР При R 4) Принужденная составляющая 5)
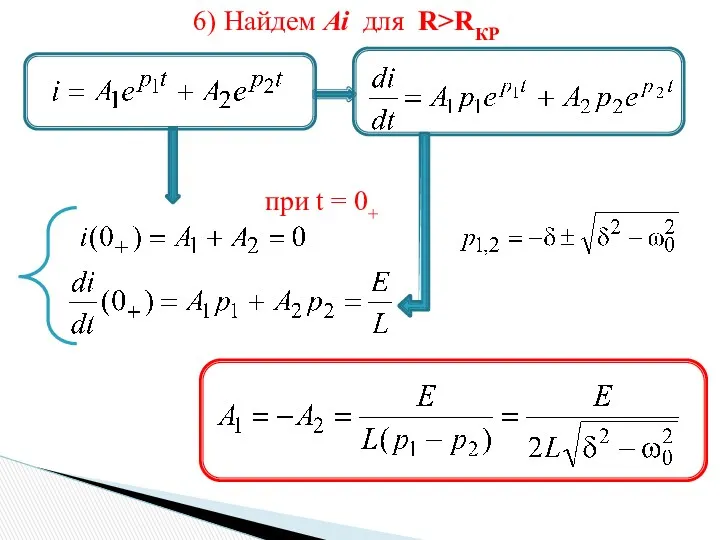
- 6. 6) Найдем Ai для R>RКР при t = 0+
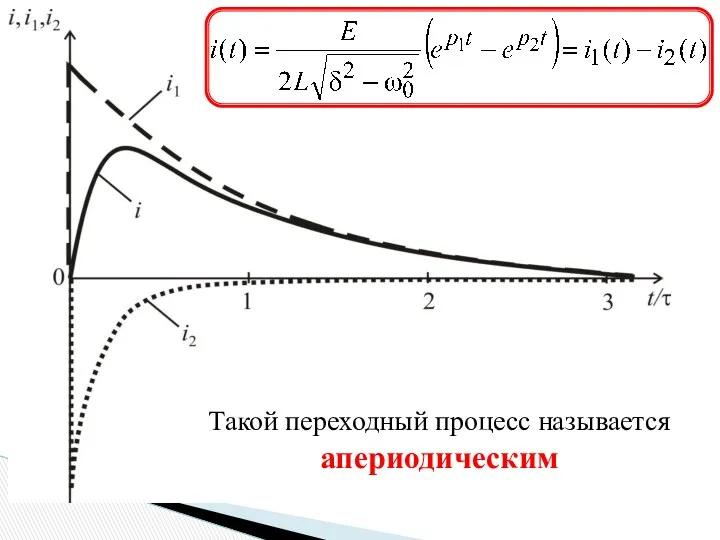
- 7. Такой переходный процесс называется апериодическим
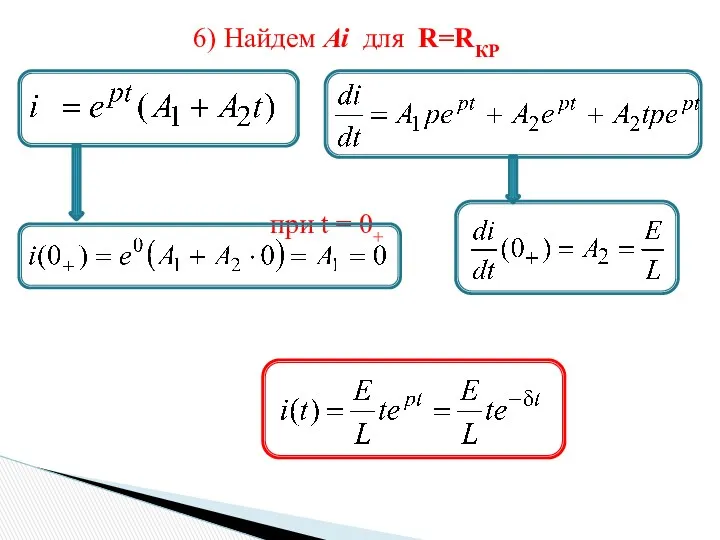
- 8. 6) Найдем Ai для R=RКР при t = 0+
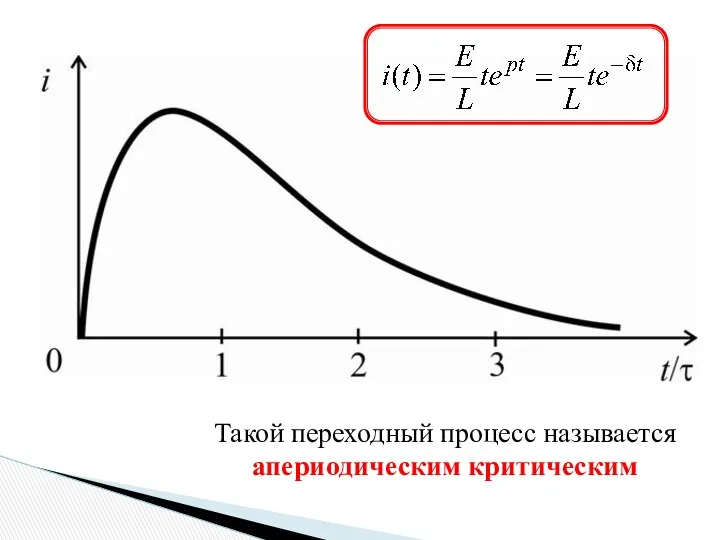
- 9. Такой переходный процесс называется апериодическим критическим
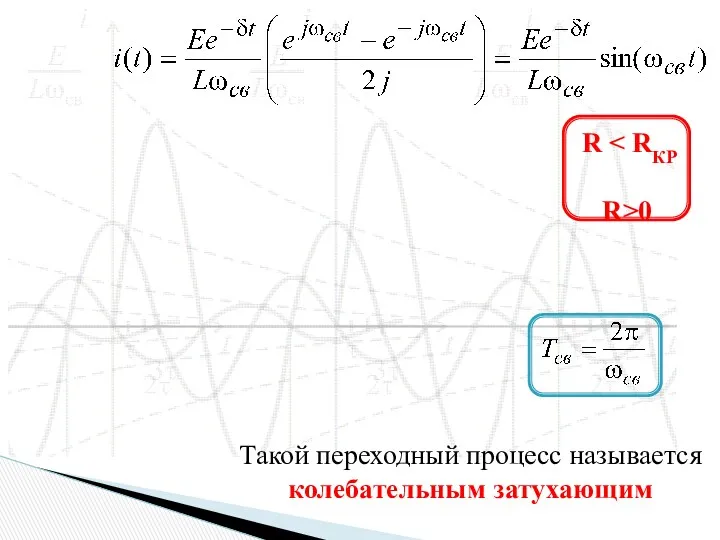
- 10. R R>0 Такой переходный процесс называется колебательным затухающим
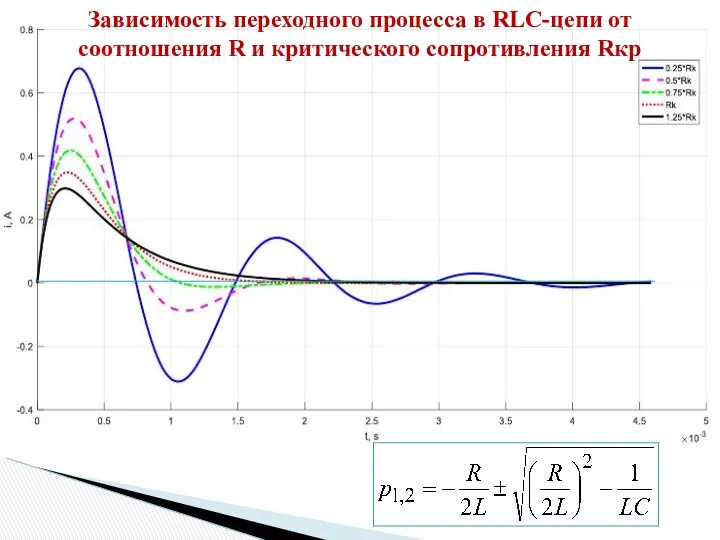
- 11. Зависимость переходного процесса в RLC-цепи от соотношения R и критического сопротивления Rкр
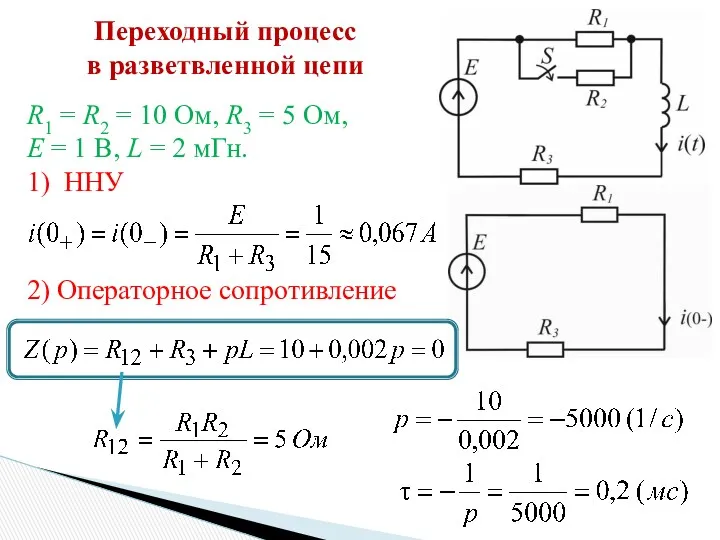
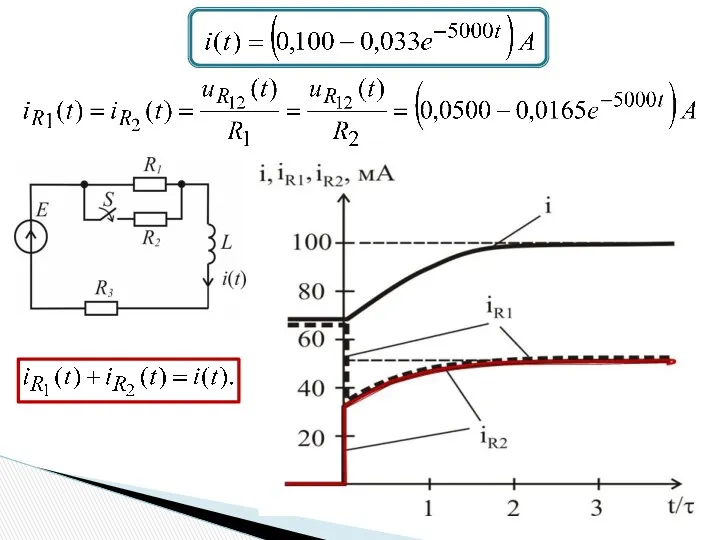
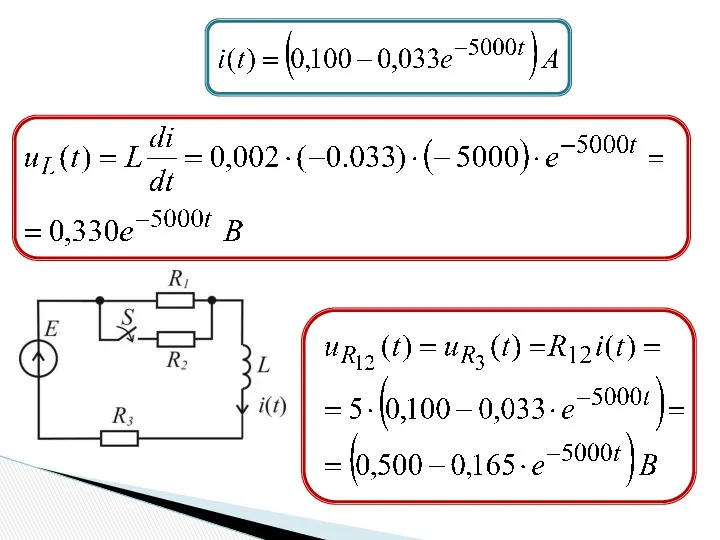
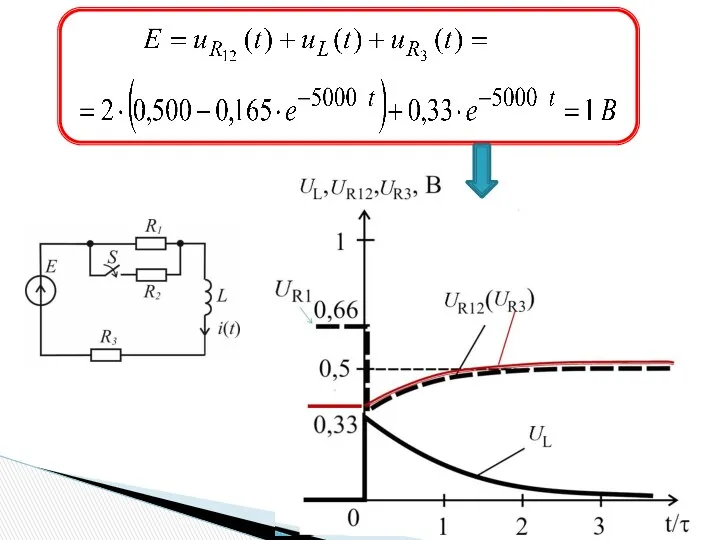
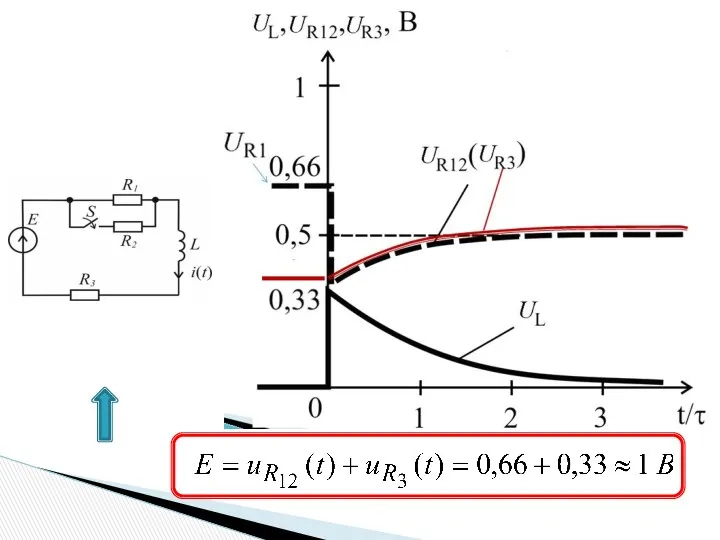
- 12. Переходный процесс в разветвленной цепи R1 = R2 = 10 Ом, R3 = 5 Ом, E
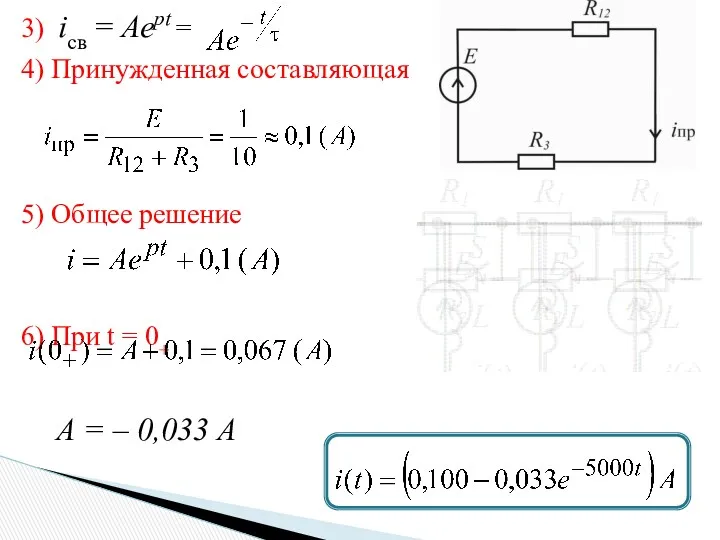
- 13. 3) iсв = Aept = 4) Принужденная составляющая 5) Общее решение 6) При t = 0+
- 18. Особенности расчета переходных процессов в нелинейных цепях Для расчета переходных процессов в нелинейных цепях: нельзя применять
- 19. Методы расчета переходных процессов нелинейный электрических цепей можно разделить на три группы: аналитические методы: метод условной
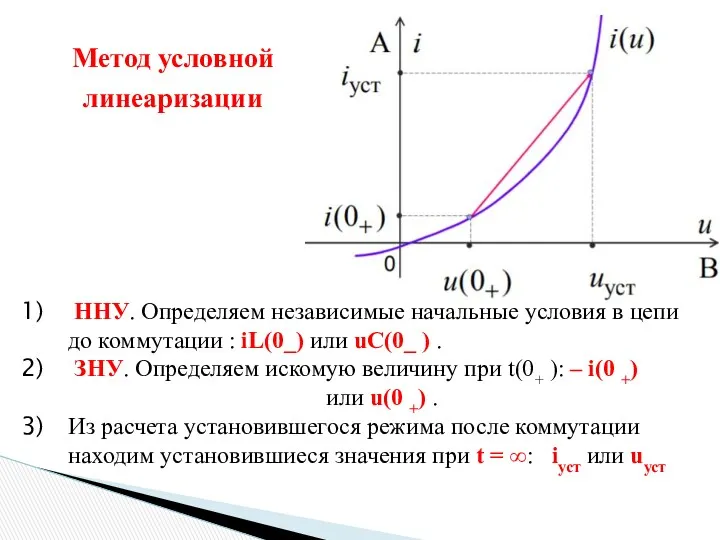
- 20. Метод условной линеаризации ННУ. Определяем независимые начальные условия в цепи до коммутации : iL(0_) или uC(0_
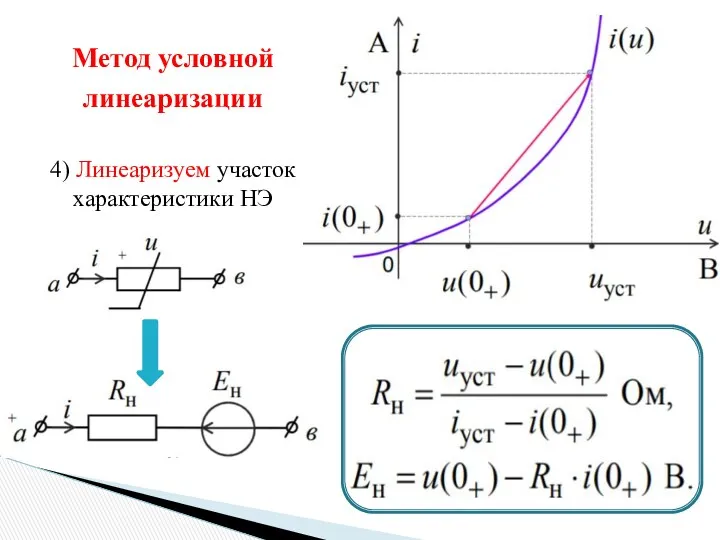
- 21. 4) Линеаризуем участок характеристики НЭ Метод условной линеаризации
- 23. Скачать презентацию


 Источники света. Распространение света
Источники света. Распространение света Природа света. Линзы
Природа света. Линзы Телескоп-рефлектор
Телескоп-рефлектор Электр тогы. Ток көздері. Ресми
Электр тогы. Ток көздері. Ресми Магнитное поле тока. Изображение магнитного поля с помощью магнитных линий
Магнитное поле тока. Изображение магнитного поля с помощью магнитных линий Сила струму. Одиниця сили струму. Вимірювання сили струму
Сила струму. Одиниця сили струму. Вимірювання сили струму Молекулярная физика. Молекулярно-кинетическая теория. Масса и размеры молекул
Молекулярная физика. Молекулярно-кинетическая теория. Масса и размеры молекул Принцип работы ядерного реактора
Принцип работы ядерного реактора Какие батарейки лучше
Какие батарейки лучше Презентация к уроку Архимедова сила
Презентация к уроку Архимедова сила Введение в нанотехнологии и материаловедение
Введение в нанотехнологии и материаловедение Сила упругости. Закон Гука
Сила упругости. Закон Гука Повторительно-обобщающий урок О, эти кванты!
Повторительно-обобщающий урок О, эти кванты! Электрические переходы. Тема 2
Электрические переходы. Тема 2 Обобщающий урок-игра по физике, 9 класс
Обобщающий урок-игра по физике, 9 класс Типы подвесок автомобилей
Типы подвесок автомобилей Радиоактивность как свидетельство сложного строения атомов. α-, β- и γ- излучения. Правила смещения при α- и βраспадах
Радиоактивность как свидетельство сложного строения атомов. α-, β- и γ- излучения. Правила смещения при α- и βраспадах Структура изображения
Структура изображения Явления взаимной индукции
Явления взаимной индукции Предмет электрохимии
Предмет электрохимии Полупроводниковые выпрямители. Лекция15
Полупроводниковые выпрямители. Лекция15 Внутрішня енергія
Внутрішня енергія Асинхронные двигатели
Асинхронные двигатели Растяжение и сжатие материалов
Растяжение и сжатие материалов Доплер эффектісі және оның қолданылуы аймағы. Доплер эффектісін қалай байқауға болады
Доплер эффектісі және оның қолданылуы аймағы. Доплер эффектісін қалай байқауға болады Accumulation of electricity. Leadacid batteries
Accumulation of electricity. Leadacid batteries Электрический заряд. Электризация. Закон сохранения заряда. Закон Кулона
Электрический заряд. Электризация. Закон сохранения заряда. Закон Кулона Физические основы механики. Кинематика материальной точки
Физические основы механики. Кинематика материальной точки