Содержание
- 2. «Теория колебаний сегодня – это широкая всеобъемлющая наука об эволюционных процессах в природе, технике и обществе,
- 3. Качественная теория дифференциальных уравнений изучает свойства решений обыкновенных дифференциальных уравнений без нахождения самих решений.
- 4. Основы ее были заложены в конце XIX века в работах А. Пуанкаре и А.М. Ляпунова. В
- 5. В чем мораль?
- 6. Очень часто встречается ситуация, когда модель рассматриваемого процесса сводится к дифференциальному уравнению. Причём, в большинстве реальных
- 7. И вот тут в полный голос звучит извечный вопрос: как быть?
- 8. Встречайте: фазовые портреты (они же фазовые диаграммы)
- 9. Динамическая система – математический объект, соответствующий реальным физическим, химическим, биологическим и др. системам, эволюция во времени,
- 10. Ответ на вопрос о том, какие режимы поведения могут устанавливаться в данной системе, можно получить из
- 11. Среди этих траекторий имеется некоторое число основных, которые и определяют качественные свойства системы. К ним относятся
- 12. Фазовое пространство в математике и физике — пространство, на котором представлено множество всех состояний системы, так,
- 13. Сущность понятия фазового пространства заключается в том, что состояние сколь угодно сложной системы представляется в нём
- 14. Фазовая плоскость — координатная плоскость, в которой по осям координат откладываются какие-либо две переменные (фазовые координаты),
- 15. Каждая точка фазовой плоскости отражает одно состояние системы и называется фазовой, изображающей или представляющей точкой. Изменение
- 16. Стрелками на фазовых траекториях показывается перемещение изображающей точки с течением времени. Полная совокупность различных фазовых траекторий
- 17. Простым языком, фазовый портрет — это то, как величины, описывающие состояние системы (т.е. динамические переменные), зависят
- 18. Линейная автономная динамическая система Рассмотрим линейную однородную систему с постоянными коэффициентами: (1) Координатную плоскость xOy называют
- 19. Положения равновесия ДС Положения равновесия системы (1) найдем, решая систему: ⎧ax + by = 0, (2)
- 20. Классификация точек покоя Собственные числа матрицы системы найдем, решая уравнение: λ2 − (a + d )λ
- 21. Устойчивость точек покоя Собственные значения матрицы системы (1) однозначно определяют устойчивости положений равновесия: характер Устойчивый узел,
- 22. 1 2 1 2 Фазовые портреты Устойчивый узел Неустойчивый узел λ ≠ λ λ λ1≠ λ2,
- 23. Фазовые портреты Устойчивый фокус Неустойчивый фокус λ1,2= α ± iβ , α λ1,2= α ± iβ
- 24. Фазовые портреты Седло Центр λ1≠ λ2, λ1 λ2 > 0 λ1,2= ± iβ , β ≠
- 25. Фазовые портреты Неустойчивый Дикритический узел имеет место для систем вида: дикритический узел когда a ≠ 0.
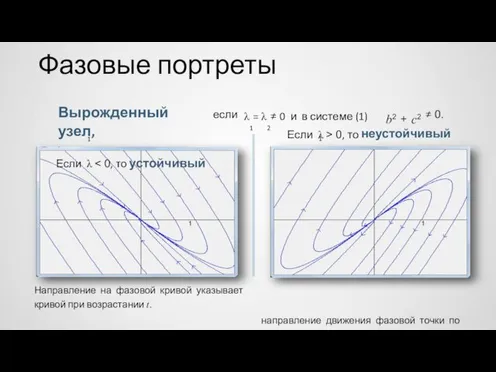
- 26. 1 направление движения фазовой точки по 1 Фазовые портреты Вырожденный узел, Если λ b2 c2 λ1=
- 27. Бесконечное множество точек покоя Если det A = 0, то система (1) имеет бесконечное новесия. При
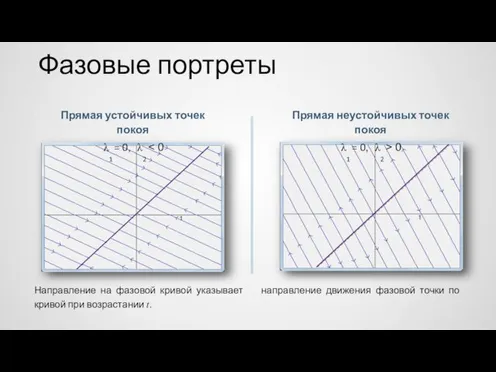
- 28. Фазовые портреты Прямая устойчивых точек покоя λ1 = 0, λ2 Прямая неустойчивых точек покоя λ1 =
- 29. Фазовые портреты Прямая неустойчивых точек покоя λ1 = λ2 = 0 Фазовые прямые будут параллельны прямой
- 30. Алгоритм построения фазового портрета 1. Определить положения равновесия, решив систему уравнений: Найти собственные значения матрицы системы,
- 31. Главные изоклины Вертикальная изоклина (ВИ) – совокупность точек фазовой плоскости, в которых касательная, проведенная к фазовой
- 32. Фазовые траектории Если положение равновесия является седлом или узлом, то существуют фазовые траектории, которые лежат на
- 33. Узел Фазовые траектории Описание фазовых траекторий уравнения (4) покоя Корни Тип точки k1 ≠ k2 Седло
- 34. Узел Фазовые траектории Тип точки покоя Описание фазовых траекторий уравнения (4) k1 = k2 Прямая y
- 35. Фазовые траектории Тип точки покоя Описание фазовых траекторий уравнения (4) Если положение равновесия является центром, то
- 36. Направление движения Если положение равновесия является узлом или фокусом, то направление движения по фазовым траекториям определяется
- 37. Направление движения Если положение равновесия является центром, то направление движения по фазовым траекториям (по часовой стрелке
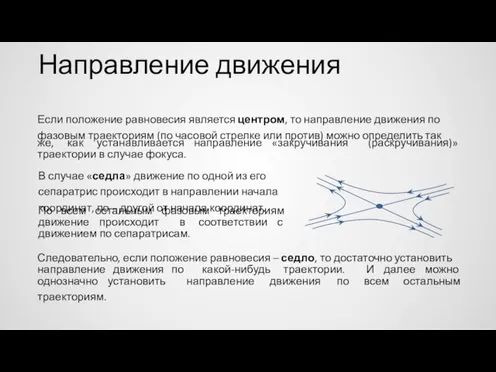
- 38. Направление движения (седло) Чтобы установить направление движения по фазовым траекториям в седла, можно воспользоваться одним из
- 39. Направление движения (седло) 3 способ Если ось x не является сепаратрисой, определить как изменяется ордината движущейся
- 40. Направление движения 4 способ* Построить в произвольной точке (x0,y0) фазовой плоскости положения равновесия) вектор скорости: (отличной
- 41. Направление движения 5 способ* Определить области «знакопостоянства» производных: dx dt dy dt = ax + by,
- 42. А сейчас нужны задачи
- 43. Ключевой принцип - от простого к сложному маленькими шагами
- 44. Пример 1 1. Система имеет единственное нулевое положение равновесия, так как det A = −6 ≠
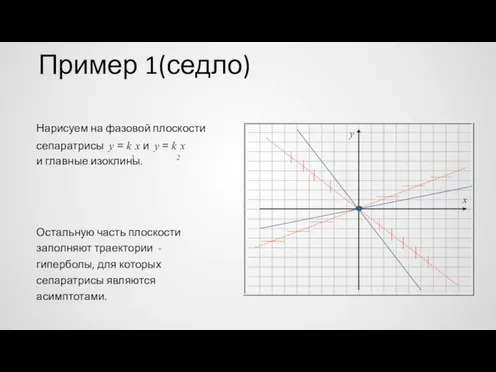
- 45. Пример 1(седло) Нарисуем на фазовой плоскости сепаратрисы y = k1x и y = k2x и главные
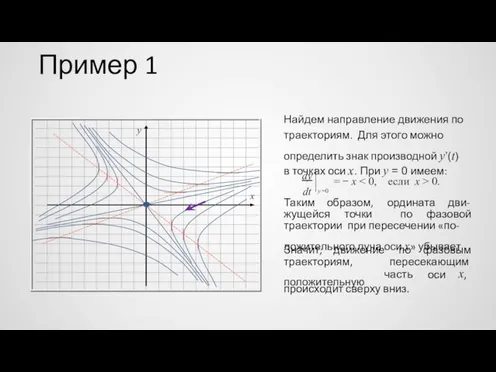
- 46. Пример 1 Найдем направление движения по траекториям. Для этого можно определить знак производной y’(t) в точках
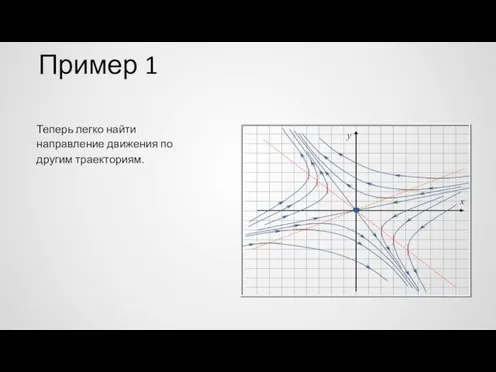
- 47. Пример 1 Теперь легко найти направление движения по другим траекториям. y x
- 48. Неоднородные ЛДС Рассмотрим линейную неоднородную систему (НЛДС) с постоянными коэффи- циентами: (5) когда γ2 + ≠
- 49. Преобразование НЛДС замену перемен- Если система (5) имеет положения равновесия, то выполнив ных: где, в случае,
- 50. Пример 2 Так как ⎧−2x − 2 y + 12 = 0, ⎩−x + 2 y
- 51. Пример 2 Построив фазовый портрет на плоскости ξPη, совместим ее с фазовой плоскостью x0y, зная, какие
- 52. Фазовые портреты НЛДС При построении фазовых портретов в случае, когда система (5) не положений равновесия, можно
- 53. Фазовые портреты НЛДС Так как выражение δ − αγ α + (a + kb) x +
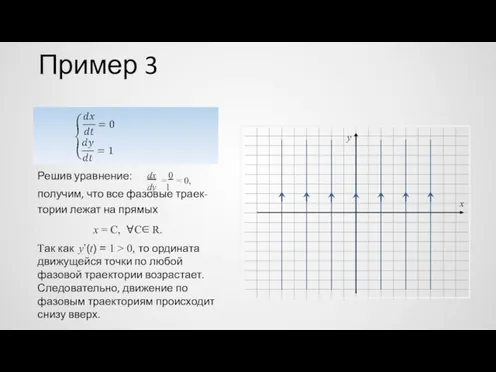
- 54. Пример 3 dx 0 Решив уравнение: = = 0, dy 1 получим, что все фазовые траек-
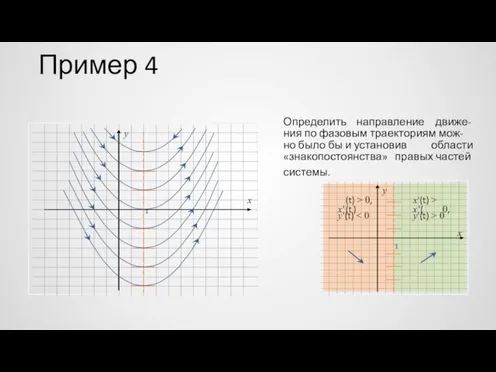
- 55. Пример 4 dy dx Решив уравнение: = x −1, получим, что фазовыми траекториями системы являются параболы:
- 56. Пример 4 Определить направление движе- y ния по фазовым траекториям мож- но было бы и установив
- 57. Хмм... Колебания в линейном случае происходят синхронно — с одной и то же частотой. В нелинейном
- 58. Это служит еще одним подтверждением того, что нелинейные колебания не являются гармоническими.
- 60. Скачать презентацию

















































 Вводный урок 7 класс
Вводный урок 7 класс История развития физики. Физика и техника
История развития физики. Физика и техника Дисциплина: Инженерная механика. Введение
Дисциплина: Инженерная механика. Введение Электризация тел. Два рода зарядов
Электризация тел. Два рода зарядов Магнитная гидродинамика
Магнитная гидродинамика Спектроскоп. Устройство, принцип работы спектроскопа
Спектроскоп. Устройство, принцип работы спектроскопа Анализ кинетической модели химических превращений. (Тема 4.4)
Анализ кинетической модели химических превращений. (Тема 4.4) Електромагнітні хвилі
Електромагнітні хвилі интегрированный урок физика+математика
интегрированный урок физика+математика Требования, предъявляемые к оборудованию кабинета физики в связи с переходом на ФГОС второго поколения
Требования, предъявляемые к оборудованию кабинета физики в связи с переходом на ФГОС второго поколения Принцип работы, устройство ,техническое обслуживание и ремонт ведущего моста ЗИЛ-130
Принцип работы, устройство ,техническое обслуживание и ремонт ведущего моста ЗИЛ-130 Векторы в физике
Векторы в физике Закон сохранения импульса
Закон сохранения импульса Ауада ұшу тақырыбына презентаия
Ауада ұшу тақырыбына презентаия Поршни. Основные части днища
Поршни. Основные части днища Асинхронды қозғалтқыш
Асинхронды қозғалтқыш Визначення середньої швидкості нерівномірного руху
Визначення середньої швидкості нерівномірного руху презентация к уроку
презентация к уроку Виды излучений. Инфракрасное излучение
Виды излучений. Инфракрасное излучение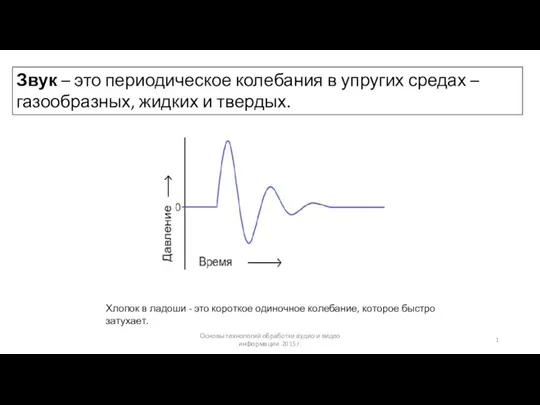 Звук. Периодическое колебание
Звук. Периодическое колебание UravneniaMaxvellaEMV2122
UravneniaMaxvellaEMV2122 Кінематика
Кінематика Рентгеновское излучение
Рентгеновское излучение Линзы. Виды линз
Линзы. Виды линз Излучение и спектры (презентация)
Излучение и спектры (презентация) Электризация тел при соприкосновении. Взаимодействие заряженных тел. Два рода зарядов. 8 класс
Электризация тел при соприкосновении. Взаимодействие заряженных тел. Два рода зарядов. 8 класс Естественнонаучная картина мира. Физические картины мира. Принципы современной физики
Естественнонаучная картина мира. Физические картины мира. Принципы современной физики Модели атомов. Опыт Резерфорда
Модели атомов. Опыт Резерфорда