Содержание
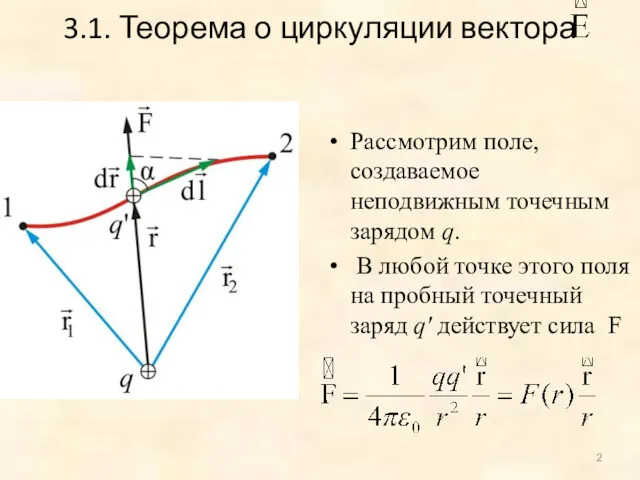
- 2. Рассмотрим поле, создаваемое неподвижным точечным зарядом q. В любой точке этого поля на пробный точечный заряд
- 3. Вычислим работу, которую совершает электростатическое поле, созданное зарядом q по перемещению заряда q' из точки 1
- 4. Полная работа при перемещении из точки 1 в точку 2 равна интегралу: Работа электростатических сил не
- 5. Если в качестве пробного заряда, перенесенного из точки 1 заданного поля в точку 2, взять положительный
- 6. Тогда вся работа равна: Такой интеграл по замкнутому контуру называется циркуляцией вектора Из независимости линейного интеграла
- 7. Электростатическое поле потенциально, т.е. обладает потенциальной энергией. Работу сил электростатического поля: Это выражение для работы можно
- 8. 3.3. Потенциал. Разность потенциалов Разные пробные заряды q',q'',… будут обладать в одной и той же точке
- 9. потенциал численно равен потенциальной энергии, которой обладает в данной точке поля единичный положительный заряд. потенциал точечного
- 10. Другое определение потенциала: потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом при
- 11. Если поле создается системой зарядов, то: Для потенциала или т.е. потенциал поля, создаваемый системой зарядов, равен
- 12. Работа сил электростатического поля через разность потенциалов между начальной и конечной точками: Работа над зарядом q
- 13. за единицу φ принимают потенциал в такой точке поля, для перемещения в которую из бесконечности единичного
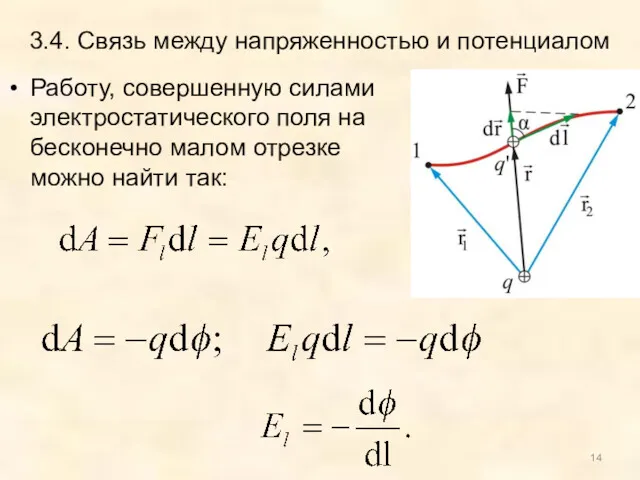
- 14. 3.4. Связь между напряженностью и потенциалом Работу, совершенную силами электростатического поля на бесконечно малом отрезке можно
- 15. Тогда По определению градиента сумма первых производных от какой-либо функции по координатам есть градиент этой функции
- 16. Где (набла) означает символический вектор, называемый оператором Гамильтона Знак минус говорит о том, что вектор направлен
- 17. Из условия следует одно важное соотношение, а именно, величина, векторного произведения для стационарных электрических полей всегда
- 18. 3.5. Силовые линии и эквипотенциальные поверхности Напряженность равна разности потенциалов U на единицу длины силовой линии.
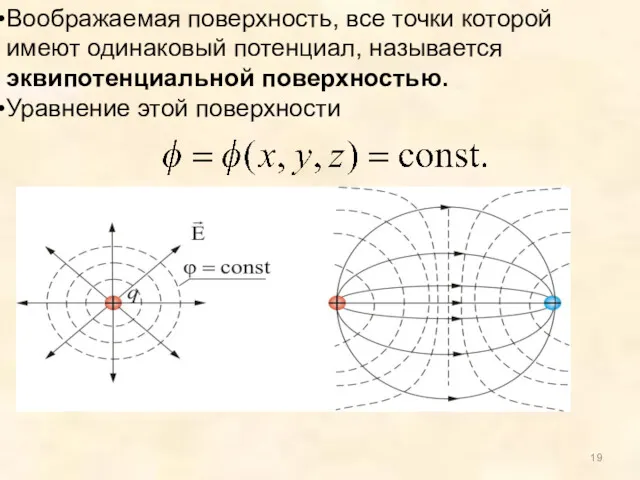
- 19. Воображаемая поверхность, все точки которой имеют одинаковый потенциал, называется эквипотенциальной поверхностью. Уравнение этой поверхности
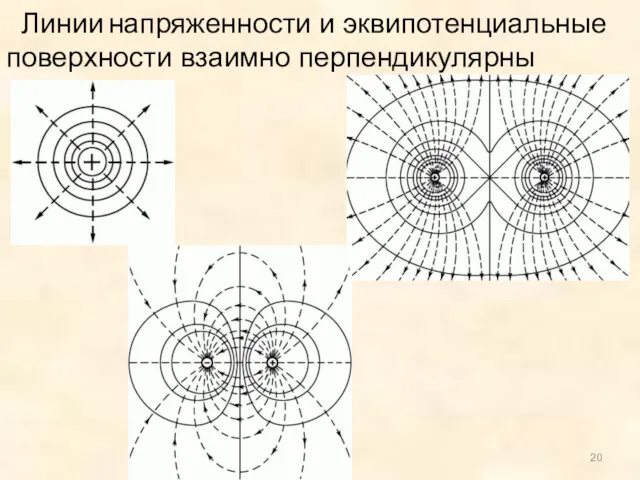
- 20. Линии напряженности и эквипотенциальные поверхности взаимно перпендикулярны
- 21. Можно по известным значениям φ найти напряженность поля в каждой точке. или по известным значениям в
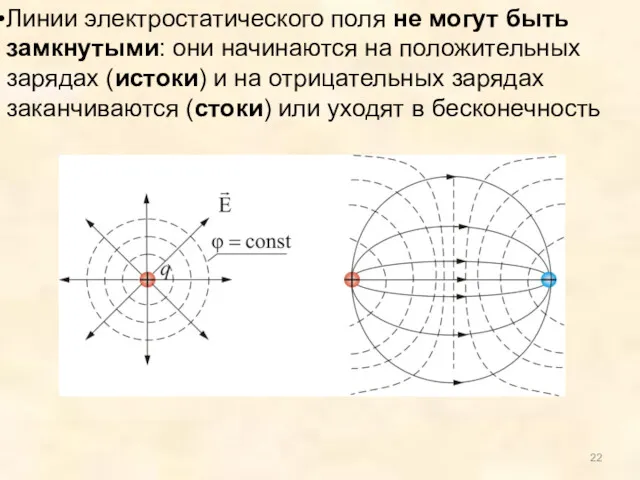
- 22. Линии электростатического поля не могут быть замкнутыми: они начинаются на положительных зарядах (истоки) и на отрицательных
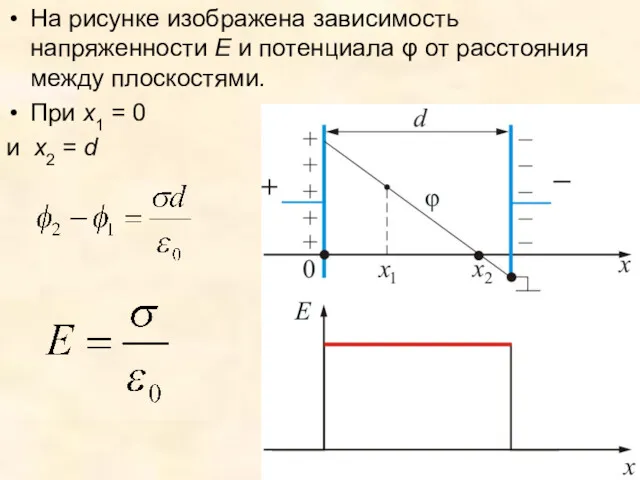
- 23. 3.7. Расчет потенциалов простейших электростатических полей 3.7.1. Разность потенциалов между двумя бесконечными заряженными плоскостями
- 24. На рисунке изображена зависимость напряженности E и потенциала φ от расстояния между плоскостями. При x1 =
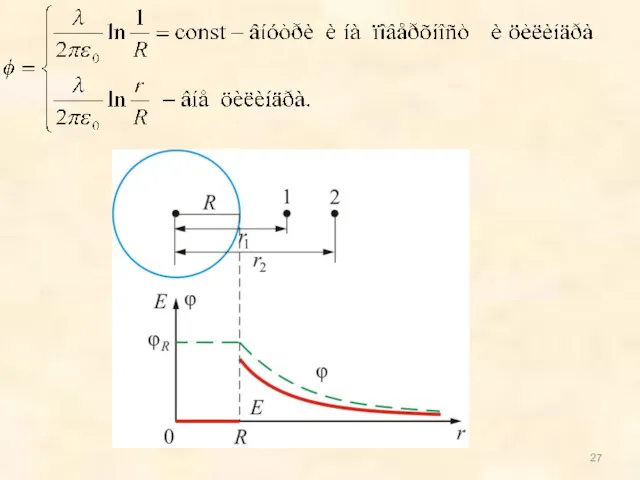
- 25. 3.7.2. Разность потенциалов между точками поля, образованного бесконечно длинной цилиндрической поверхностью С помощью теоремы Остроградского-Гаусса мы
- 26. Тогда, т.к. отсюда следует, что разность потенциалов в произвольных точках 1 и 2 будет равна:
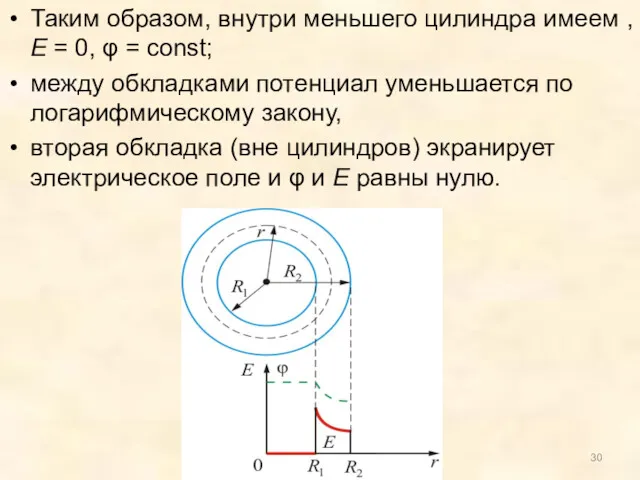
- 28. 3.7.3. Разность потенциалов между обкладками цилиндрического конденсатора
- 29. Т.к. , то
- 30. Таким образом, внутри меньшего цилиндра имеем , Е = 0, φ = const; между обкладками потенциал
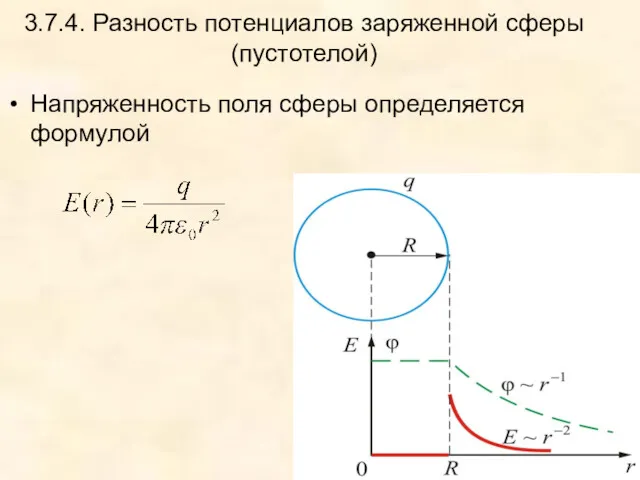
- 31. 3.7.4. Разность потенциалов заряженной сферы (пустотелой) Напряженность поля сферы определяется формулой
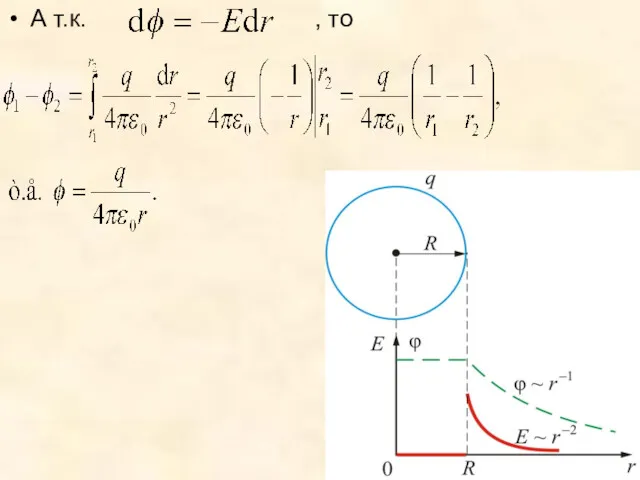
- 32. А т.к. , то
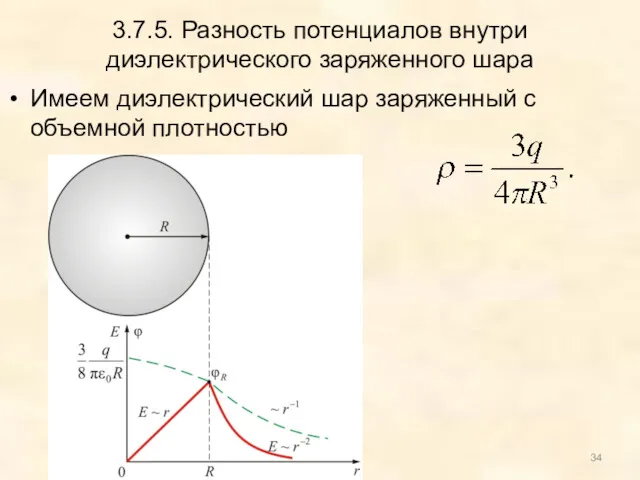
- 34. 3.7.5. Разность потенциалов внутри диэлектрического заряженного шара Имеем диэлектрический шар заряженный с объемной плотностью
- 35. Напряженность поля шара, вычисленная с помощью теоремы Остроградского-Гаусса:
- 36. Отсюда найдем разность потенциалов шара: или
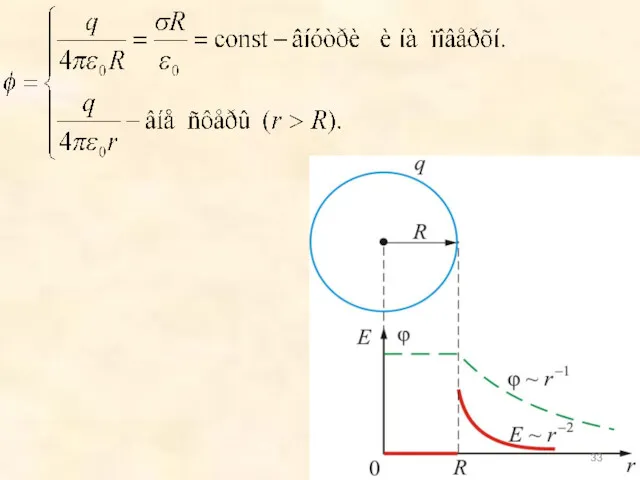
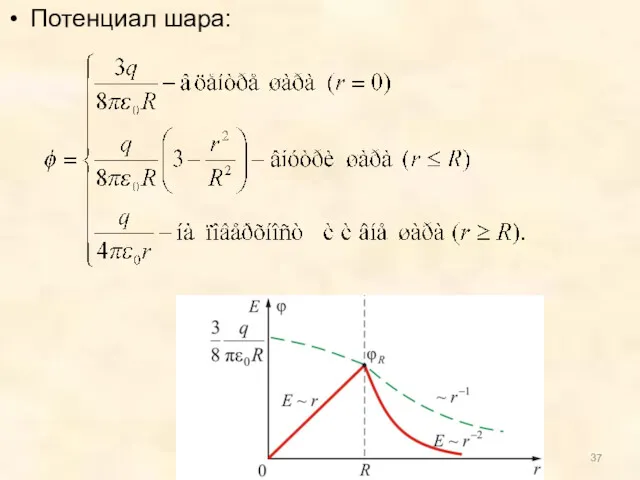
- 37. Потенциал шара:
- 39. Скачать презентацию























 Технические измерения. Допуски и посадки гладких цилиндрических соединений деталей (гцс)
Технические измерения. Допуски и посадки гладких цилиндрических соединений деталей (гцс) Закон всемирного тяготения. Решение задач
Закон всемирного тяготения. Решение задач Презентация к уроку на тему: Цепная Ядерная реакция
Презентация к уроку на тему: Цепная Ядерная реакция Решение задач по теме: Давление в жидкости
Решение задач по теме: Давление в жидкости Вантажопідйомні машини. Держгірпромнагляд
Вантажопідйомні машини. Держгірпромнагляд Лекция 4. Основные показатели кристаллизации
Лекция 4. Основные показатели кристаллизации Система питания дизельного двигателя
Система питания дизельного двигателя Бинарный урок - конференция по физике и химии
Бинарный урок - конференция по физике и химии Схема строения ракеты
Схема строения ракеты Дисперсия света. Виды спектров
Дисперсия света. Виды спектров Магнитные свойства вещества
Магнитные свойства вещества Түйіндік потенциалдар әдісі. Екі түйіндер әдісі. Беттестіру әдісі. Баламалық генератор әдісі
Түйіндік потенциалдар әдісі. Екі түйіндер әдісі. Беттестіру әдісі. Баламалық генератор әдісі Автоматика и управление. Тема 4. Частотные характеристики линейных стационарных автоматических систем
Автоматика и управление. Тема 4. Частотные характеристики линейных стационарных автоматических систем Строение и эволюция Вселенной
Строение и эволюция Вселенной Элементы биофизики зрения
Элементы биофизики зрения Малоугловое рассеяние нейтронов и рентгеновских лучей в неупорядоченных средах (SANS, USANS и SAXS)
Малоугловое рассеяние нейтронов и рентгеновских лучей в неупорядоченных средах (SANS, USANS и SAXS) Проводники с током в магнитном поле. Лекция 8
Проводники с током в магнитном поле. Лекция 8 Ракетные двигатели, их значимость, устройство и принцип работы
Ракетные двигатели, их значимость, устройство и принцип работы Планировка участка ремонта ГРМ и КШМ
Планировка участка ремонта ГРМ и КШМ Технологический процесс изготовления детали Шестерня
Технологический процесс изготовления детали Шестерня Классификация физических методов
Классификация физических методов Презентация по физике Магнитное поле
Презентация по физике Магнитное поле Законы фотоэффекта. Квантовые свойства вещества и света
Законы фотоэффекта. Квантовые свойства вещества и света Современное оборудование кондитерского цеха
Современное оборудование кондитерского цеха Приложение к уроку
Приложение к уроку Учет по уровню. Общие положения
Учет по уровню. Общие положения Виштовхувальна сила. Закон Архімеда
Виштовхувальна сила. Закон Архімеда Свободное падение тел. Движение с ускорением свободного падения
Свободное падение тел. Движение с ускорением свободного падения