Содержание
- 2. 5.1. Теорема о циркуляции вектора В предыдущей теме было показано, что взаимодействие между покоящимися зарядами осуществляется
- 3. Существует и другой способ описания поля – с помощью потенциала. Однако для этого необходимо сначала доказать,
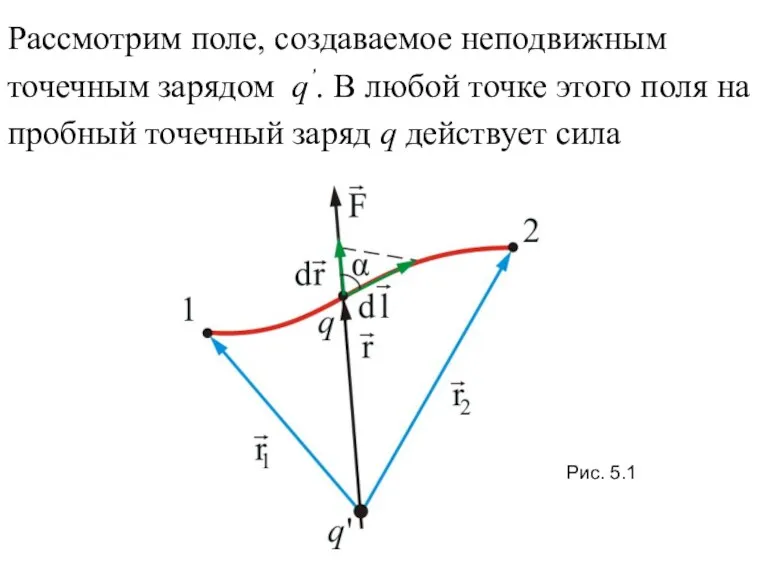
- 4. Рассмотрим поле, создаваемое неподвижным точечным зарядом q’. В любой точке этого поля на пробный точечный заряд
- 5. где F(r) – модуль вектора силы , – единичный вектор, определяющий положение заряда q относительно ,
- 6. Для того, чтобы доказать, что электростатическое поле потенциально, нужно доказать, что силы электростатического поля консервативны. Из
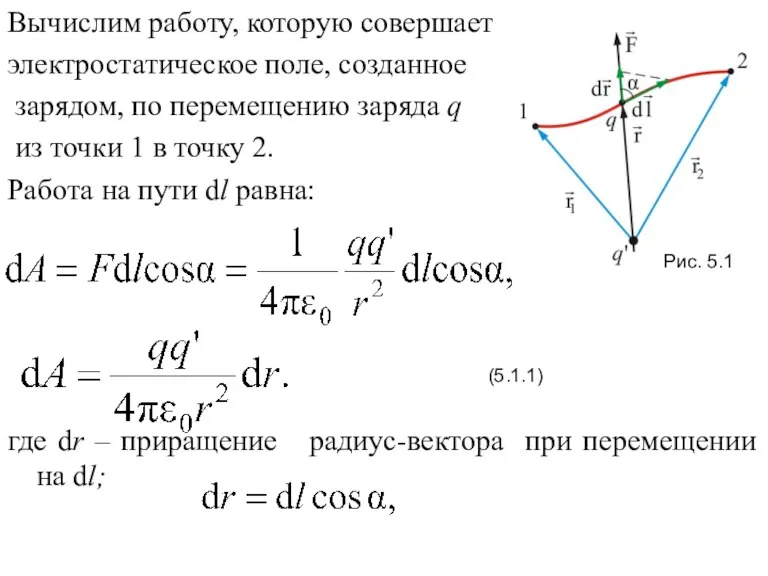
- 7. Вычислим работу, которую совершает электростатическое поле, созданное зарядом, по перемещению заряда q из точки 1 в
- 8. Полная работа при перемещении из точки 1 в точку 2 равна интегралу: (5.1.2)
- 9. Работа электростатических сил не зависит от формы пути, а только лишь от координат начальной и конечной
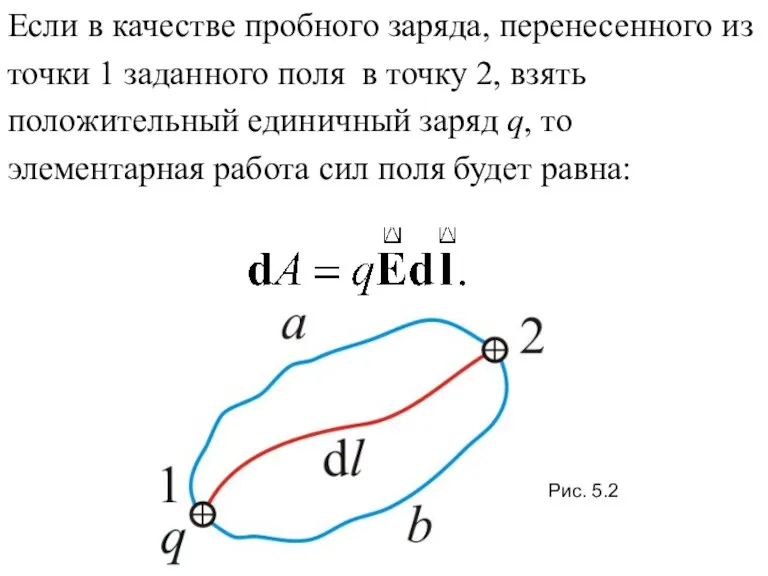
- 10. Если в качестве пробного заряда, перенесенного из точки 1 заданного поля в точку 2, взять положительный
- 11. Тогда вся работа равна: (5.1.3) Такой интеграл по замкнутому контуру называется циркуляцией вектора Из независимости линейного
- 12. Для доказательства теоремы разобьем произвольно замкнутый путь на две части: 1а2 и 2b1 (рис.5.2). Из сказанного
- 13. Теорема о циркуляции позволяет сделать ряд важных выводов, практически не прибегая к расчетам. Рассмотрим два простых
- 14. Рис. 5.3,а Пример 2. Возможна ли конфигурация электростатического поля как на рисунке 5.3,а?
- 15. Рис. 5.3,б Стрелки здесь показывают направление обхода. На вертикальных участках перпендикулярно и А = 0. Остаются
- 16. 5.2. Работа сил электростатического поля. Потенциальная энергия Мы сделали заключение, что электростатическое поле потенциально. Следовательно, можно
- 17. Исходя из принципа суперпозиции сил , можно показать, что общая работа А будет равна сумме работ
- 18. Работу сил электростатического поля можно выразить через убыль потенциальной энергии – разность двух функций состояний: (5.2.2)
- 19. 5.3. Потенциал. Разность потенциалов Разные пробные заряды q1, q2,… будут обладать в одной и той же
- 20. Из этого выражения следует, что потенциал численно равен потенциальной энергии, которой обладает в данной точке поля
- 21. Подставив в (3.3.1.) значение потенциальной энергии (5.2.4), получим для потенциала точечного заряда следующее выражение: (3.3.2) Потенциал,
- 22. физический смысл имеет не потенциал, а разность потенциалов, поэтому договорились считать, что потенциал точки, удаленной в
- 23. Другое определение потенциала: т.е. потенциал численно равен работе, которую совершают силы поля над единичным положительным зарядом
- 24. Если поле создается системой зарядов, то, используя принцип суперпозиции, получаем: (5.3.3) Тогда и для потенциала или
- 25. Выразим работу сил электростатического поля через разность потенциалов между начальной и конечной точками: Таким образом, работа
- 26. Формулу можно использовать для установления единиц потенциала: за единицу φ принимают потенциал в такой точке поля,
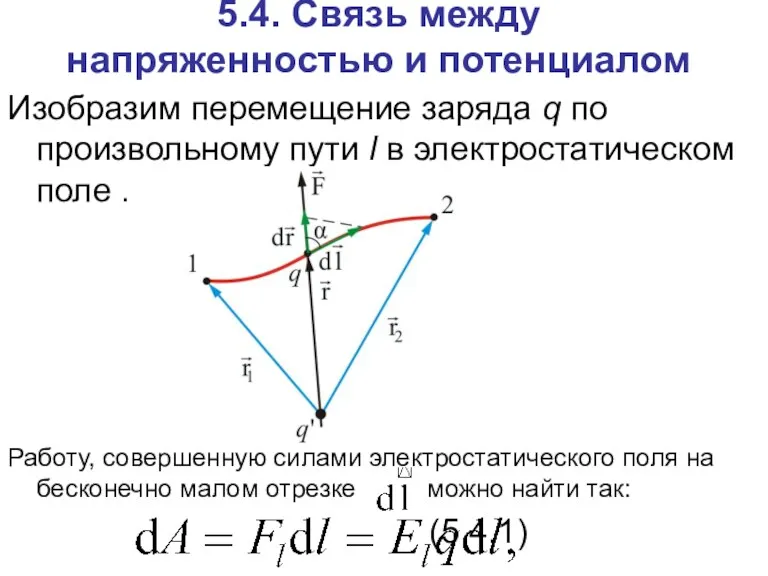
- 27. 5.4. Связь между напряженностью и потенциалом Изобразим перемещение заряда q по произвольному пути l в электростатическом
- 28. эта работа, если она совершена электростатическим полем, равна убыли потенциальной энергии заряда, перемещенного на расстоянии dl:
- 29. Для ориентации dl (направление перемещения) в пространстве, надо знать проекции на оси координат: где i, j,
- 30. Коротко связь между и φ записывается так: (3.4.4) или так: (3.4.5) где (набла) означает символический вектор,
- 31. 5.5. Безвихревой характер электростатического поля Из условия следует одно важное соотношение, а именно, величина, векторного произведения
- 32. Величина называется ротором или вихрем Мы получаем важнейшее уравнение электростатики: (5.5.1) Таким образом кулоновское электростатическое поле
- 33. Согласно теореме Стокса, присутствует следующая связь между контурным и поверхностным интегралами: где контур L ограничивающий поверхность
- 35. Скачать презентацию




























 Introduction to Quantum Mechanic
Introduction to Quantum Mechanic Replacement of Dryer
Replacement of Dryer Организация технического обслуживания и ремонта электрического и электромеханического оборудования
Организация технического обслуживания и ремонта электрического и электромеханического оборудования Sunlight and space travel
Sunlight and space travel Теплотехника Техническая термодинамика и теплопередача
Теплотехника Техническая термодинамика и теплопередача Влияние мобильного телефона на здоровье школьника
Влияние мобильного телефона на здоровье школьника Открытие и применение закона всемирного тяготения
Открытие и применение закона всемирного тяготения Фізичні та хімічні явища
Фізичні та хімічні явища Как стать миллионером знаний по атомной физике?
Как стать миллионером знаний по атомной физике? Композиты - древний материал будущего
Композиты - древний материал будущего Іонізаційний метод індикації
Іонізаційний метод індикації Конструктивное исполнение 2-х и 4-х тактных дизелей
Конструктивное исполнение 2-х и 4-х тактных дизелей Теорема Гаусса для вектора магнитной индукции
Теорема Гаусса для вектора магнитной индукции Подготовка к ГИА по физике 2013
Подготовка к ГИА по физике 2013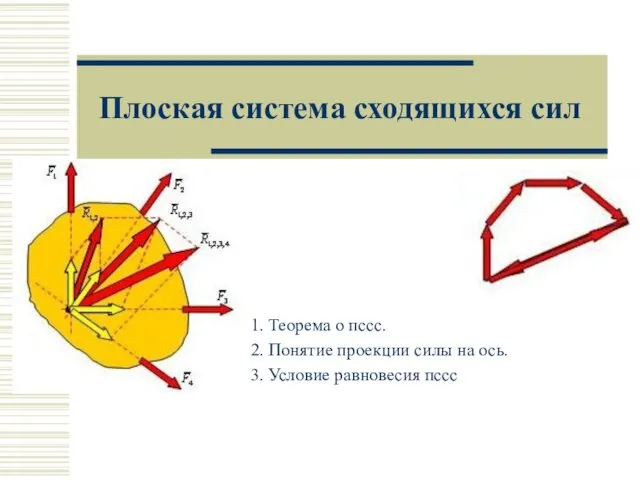 Плоская система сходящихся сил
Плоская система сходящихся сил Ядро. Ядерные силы
Ядро. Ядерные силы Электрические машины постоянного тока
Электрические машины постоянного тока Индикаторы. Промышленные регуляторы
Индикаторы. Промышленные регуляторы Химическая кинетика. Лекция 9
Химическая кинетика. Лекция 9 Силы, действующие на мотоцикл
Силы, действующие на мотоцикл Урок физики в 7 классе Вес воздуха. Атмосферное давление
Урок физики в 7 классе Вес воздуха. Атмосферное давление Основы слесарно-сборочных и электромонтажных работ. Обязанности электромонтера по ремонту и обслуживанию электрооборудования
Основы слесарно-сборочных и электромонтажных работ. Обязанности электромонтера по ремонту и обслуживанию электрооборудования Распределительное устройство 10 кВ
Распределительное устройство 10 кВ Схематизация опор. Определение реакций
Схематизация опор. Определение реакций Магнитное поле в веществе. Система уравнений Максвелла. Тема 18
Магнитное поле в веществе. Система уравнений Максвелла. Тема 18 Ажырамалы қосылыстар
Ажырамалы қосылыстар Полупроводниковые выпрямители. Лекция15
Полупроводниковые выпрямители. Лекция15 Исследование напряженного состояния в точке тела. Тема 7
Исследование напряженного состояния в точке тела. Тема 7