Содержание
- 2. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ Пространственной будем называть систему сил, линии действия которых имеют любые направления в пространстве.
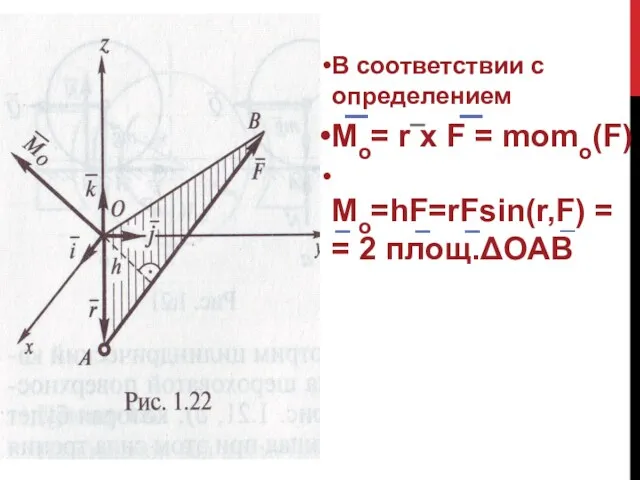
- 3. В соответствии с определением Мо= r x F = momo(F) Мо=hF=rFsin(r,F) = = 2 площ.ΔОАВ
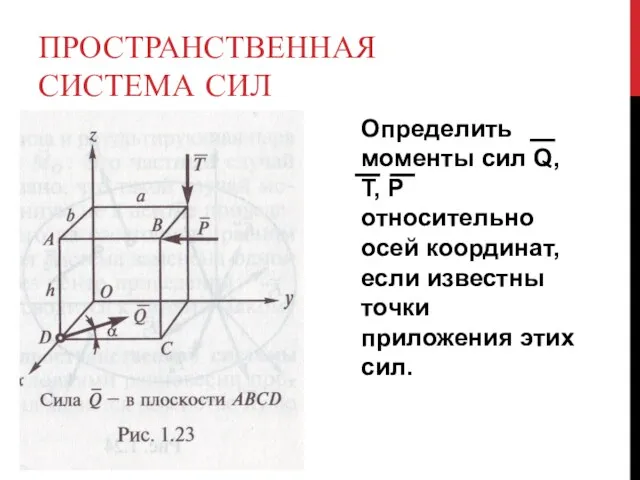
- 4. ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ Определить моменты сил Q, T, P относительно осей координат, если известны точки приложения
- 5. РЕШЕНИЕ: 1. Определяем моменты силы T относительно осей координат: momx(T) = -Ta; momy(T) = 0 (так
- 6. ПРИВЕДЕНИЕ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ К ЗАДАННОМУ ЦЕНТРУ Пространственная система сил, действующих на АТТ, может быть заменена
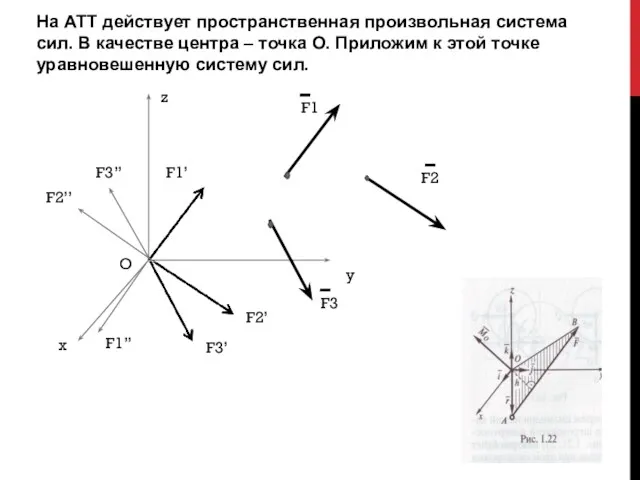
- 7. На АТТ действует пространственная произвольная система сил. В качестве центра – точка О. Приложим к этой
- 8. Заменим действующую систему пространственных сходящихся сил равнодействующей R = F1’+F2’ +F3’. Вычислим моменты всех оставшихся сил
- 9. АНАЛИТИЧЕСКИЕ ВЫРАЖЕНИЯ ДЛЯ ОПРЕДЕЛЕНИЯ ГЛАВНОГО ВЕКТОРА И ГЛАВНОГО МОМЕНТА Определяем главный вектор и главный момент аналитически,
- 10. АНАЛИТИЧЕСКИЕ УСЛОВИЯ РАВНОВЕСИЯ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ R=0; Mo = 0 Поскольку R = √Rx2 +Ry2 +Rz2
- 11. РАСЧЕТ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ Момент силы относительно точки как вектор Момент силы относительно точки в пространстве
- 12. Известно, что всякий вектор можно разложить по осям координат: Mo=Mxi + Myj +Mzk ,где i, j,
- 13. МОМЕНТ СИЛЫ ОТНОСИТЕЛЬНО ОСИ Моментом силы F относительно оси z (рис. 1.25), называется алгебраическая величина, абсолютное
- 14. В случае пространственной системы сил главным моментом относительно точки называется векторная сумма моментов всех сил системы
- 15. РАВНОВЕСИЕ ТВЕРДОГО ТЕЛА ПОД ДЕЙСТВИЕМ ПРОИЗВОЛЬНОЙ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ СИЛ Для равновесия твердого тела под действием произвольной
- 16. КОНТРОЛЬНЫЕ ВОПРОСЫ 1. Какие силы называются пространственными? 2. Как определяется вектор момента силы F, расположенной в
- 17. КИНЕМАТИКА ТОЧКИ Кинематика – это раздел механики, в котором изучается движение материальных тел в пространстве с
- 18. СПОСОБЫ ЗАДАНИЯ ДВИЖЕНИЯ МАТЕРИАЛЬНОЙ ТОЧКИ Траектория – линия движения. Естественный способ, если известны: 1) траектория точки;
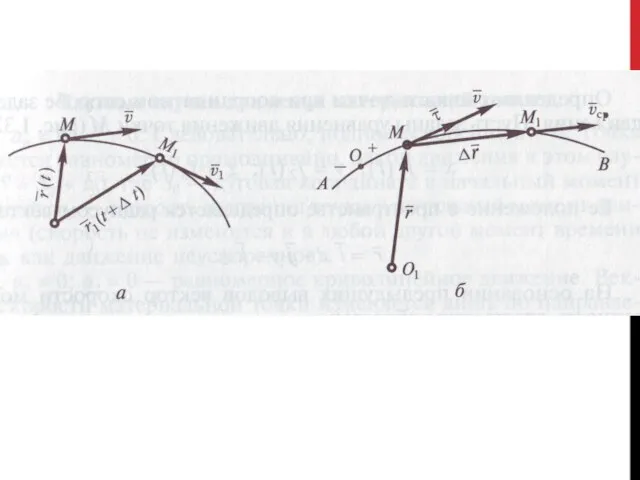
- 19. Векторный способ задания движения : r=r(t). Положение точки определяется радиусом-вектором r, проведенным из центра О в
- 20. КООРДИНАТНЫЙ СПОСОБ ЗАДАНИЯ ДВИЖЕНИЯ Должны быть известны зависимости, показывающие изменения во времени координаты в пространстве: x=f1(t);
- 21. СКОРОСТЬ ТОЧКИ Скорость характеризует быстроту и направление движения точки. Поскольку v - это производная r=r(t), то
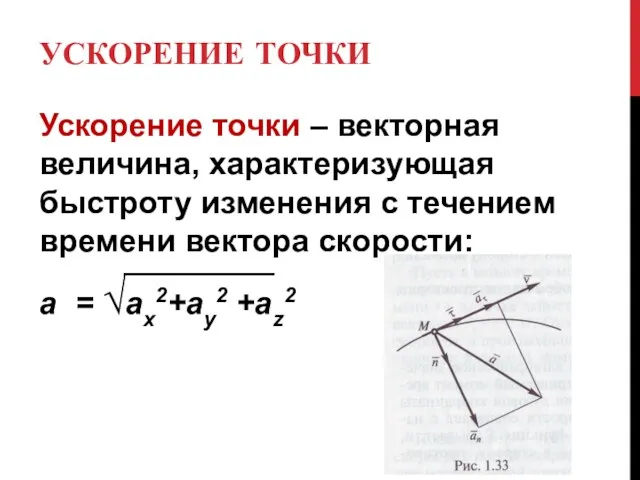
- 23. УСКОРЕНИЕ ТОЧКИ Ускорение точки – векторная величина, характеризующая быстроту изменения с течением времени вектора скорости: а
- 24. При естественном способе задания траектории движения материальной точки ее вектор ускорения можно разложить по естественным осям
- 26. Скачать презентацию


















 Аэродинамика и летно-технические данные вертолёта. Тема №1. Основные понятия о несущей поверхности. Лекция №2
Аэродинамика и летно-технические данные вертолёта. Тема №1. Основные понятия о несущей поверхности. Лекция №2 Нормативные документы. Защита от шума. Проектирование звукоизоляции ограждающих конструкций жилых и общественных зданий
Нормативные документы. Защита от шума. Проектирование звукоизоляции ограждающих конструкций жилых и общественных зданий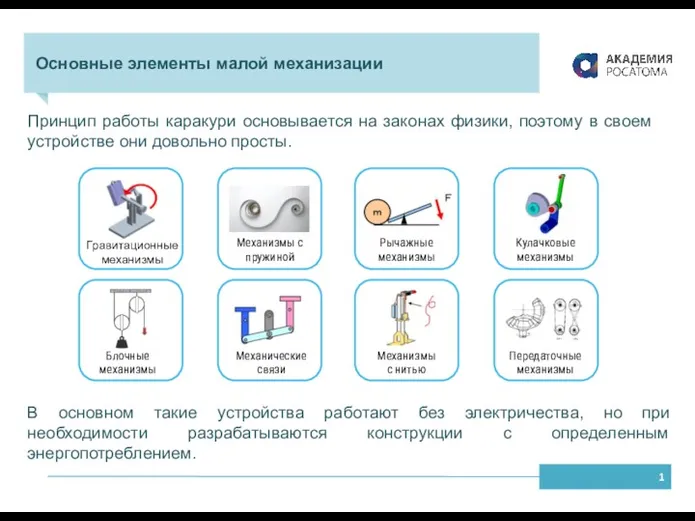 Базовые механизмы каракури. Основные элементы малой механизации
Базовые механизмы каракури. Основные элементы малой механизации Модель урока по теме Тела и их взаимодействие. Инерциальное движение.
Модель урока по теме Тела и их взаимодействие. Инерциальное движение. Протипожежна та аварійно-рятувальна техніка. Улаштування і технічне обслуговування агрегатів силової передачі (9)
Протипожежна та аварійно-рятувальна техніка. Улаштування і технічне обслуговування агрегатів силової передачі (9) Разработка урока Закон сохранения импульса
Разработка урока Закон сохранения импульса Презентация к уроку: Физика и дорожная безопасность
Презентация к уроку: Физика и дорожная безопасность Обучение физике на основе индивидуального и дифференцированного подхода
Обучение физике на основе индивидуального и дифференцированного подхода Воздух и атмосфера
Воздух и атмосфера Замена электродвигателей СТД 8000 на электродвигатели марки Нидек на ЛПДС Чепурского АК Транснефть
Замена электродвигателей СТД 8000 на электродвигатели марки Нидек на ЛПДС Чепурского АК Транснефть A4CFx – New Alpha. Power Train Variation Engine
A4CFx – New Alpha. Power Train Variation Engine Өлшеу қателіктері
Өлшеу қателіктері Аэродинамика и летно-технические данные вертолёта. Тема №1. Аэродинамическая компоновка вертолета. Групповое занятие №4
Аэродинамика и летно-технические данные вертолёта. Тема №1. Аэродинамическая компоновка вертолета. Групповое занятие №4 Устройство автомобиля – шасси. Подвеска автомобиля
Устройство автомобиля – шасси. Подвеска автомобиля Электромагнитное поле
Электромагнитное поле Понятие о технической системе. 6 класс
Понятие о технической системе. 6 класс Диффузия
Диффузия Конструкция двигателя и рабочие процессы
Конструкция двигателя и рабочие процессы Что общего у этих сосудов?
Что общего у этих сосудов? Презентация Испарение и конденсация
Презентация Испарение и конденсация Равномерное прямолинейное движение
Равномерное прямолинейное движение Законы аэродинамики
Законы аэродинамики Глава 3. Работа и энергия. Тема §1. Энергия, работа, мощность
Глава 3. Работа и энергия. Тема §1. Энергия, работа, мощность Плавание тел (фгос)
Плавание тел (фгос) Установочная лекция для студентов 1го курса. ИБФО (ускоренная форма обучения)
Установочная лекция для студентов 1го курса. ИБФО (ускоренная форма обучения) Связь физики с различными сферами жизни
Связь физики с различными сферами жизни Прямолинейное равномерное и равнопеременное движение. Тест
Прямолинейное равномерное и равнопеременное движение. Тест Статические характеристики средств измерений. (Лекция 2)
Статические характеристики средств измерений. (Лекция 2)