Содержание
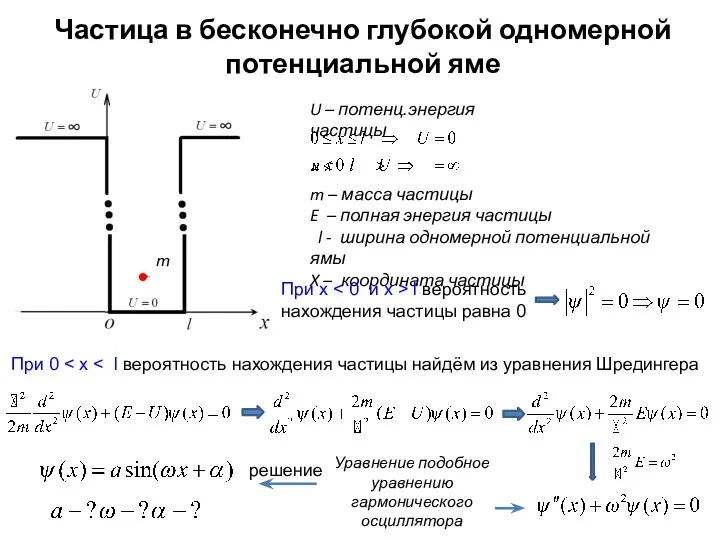
- 2. Частица в бесконечно глубокой одномерной потенциальной яме U – потенц.энергия частицы m – масса частицы E
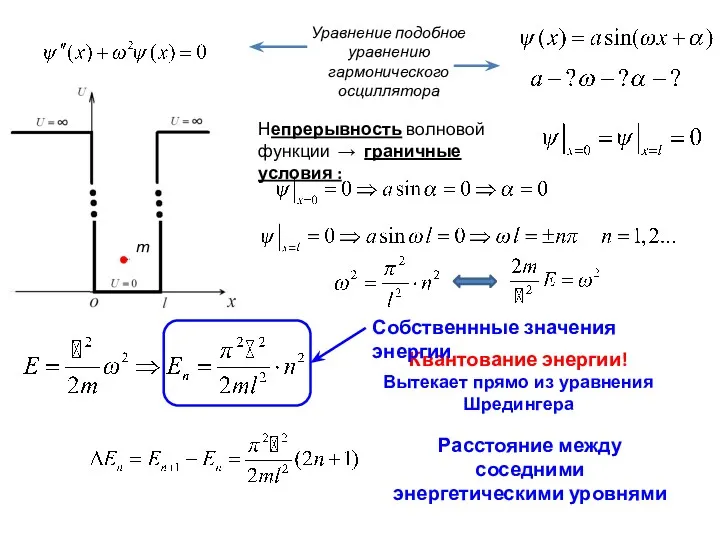
- 3. Непрерывность волновой функции → граничные условия : Уравнение подобное уравнению гармонического осциллятора Квантование энергии! Вытекает прямо
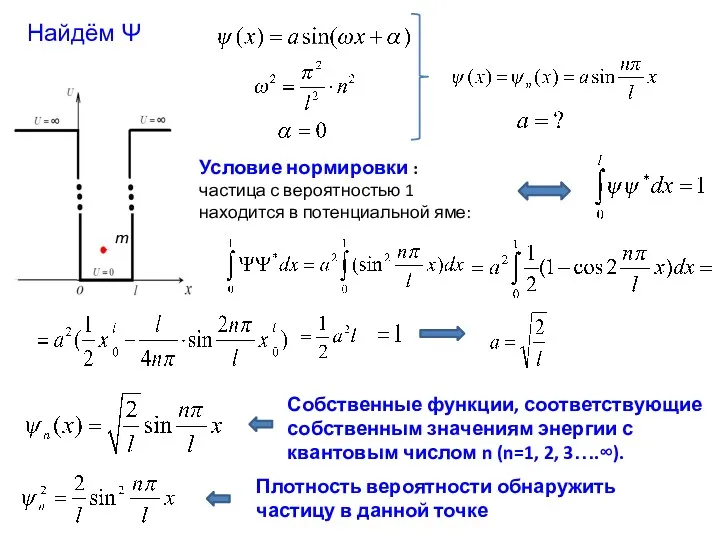
- 4. Собственные функции, соответствующие собственным значениям энергии с квантовым числом n (n=1, 2, 3….∞). Условие нормировки :
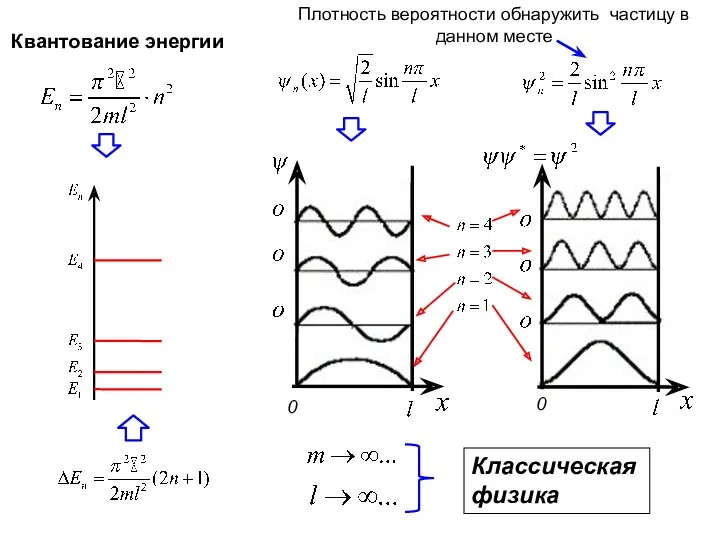
- 5. Классическая физика
- 6. Найдём масштаб квантования энергии. Пример 1: электрон, m≈10-30 кг, размер ямы l=10 см (свободный электрон в
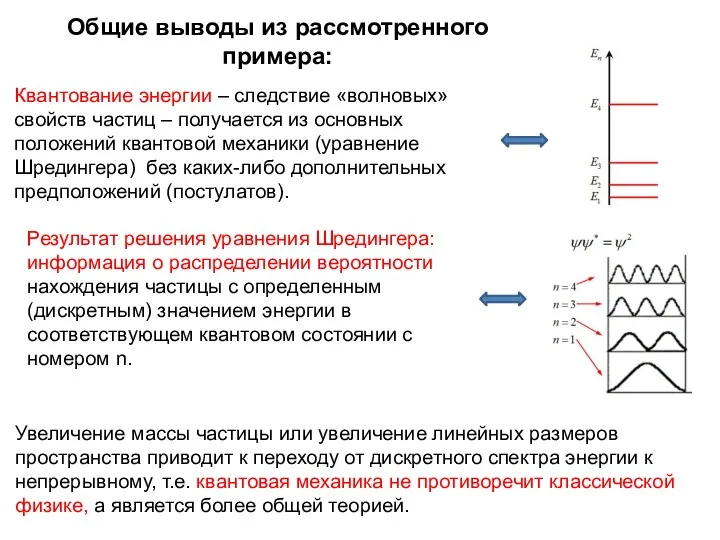
- 7. Общие выводы из рассмотренного примера: Квантование энергии – следствие «волновых» свойств частиц – получается из основных
- 8. Квантово-механическая модель атома водорода. Квантовые числа.
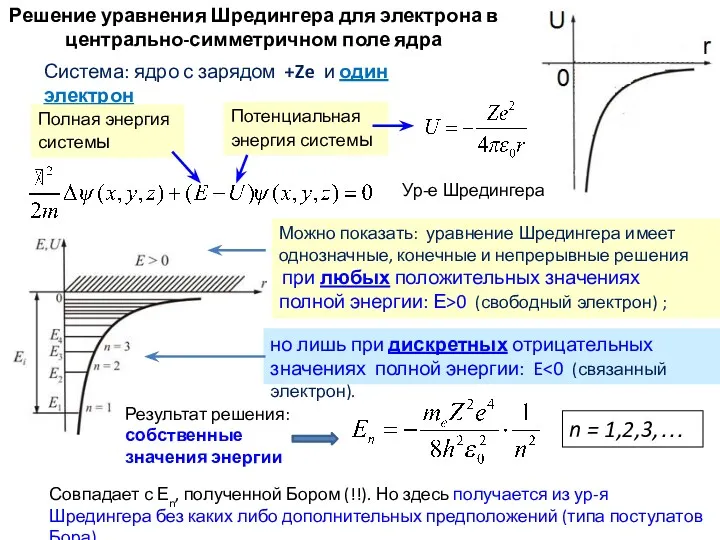
- 9. Система: ядро с зарядом +Ze и один электрон Решение уравнения Шредингера для электрона в центрально-симметричном поле
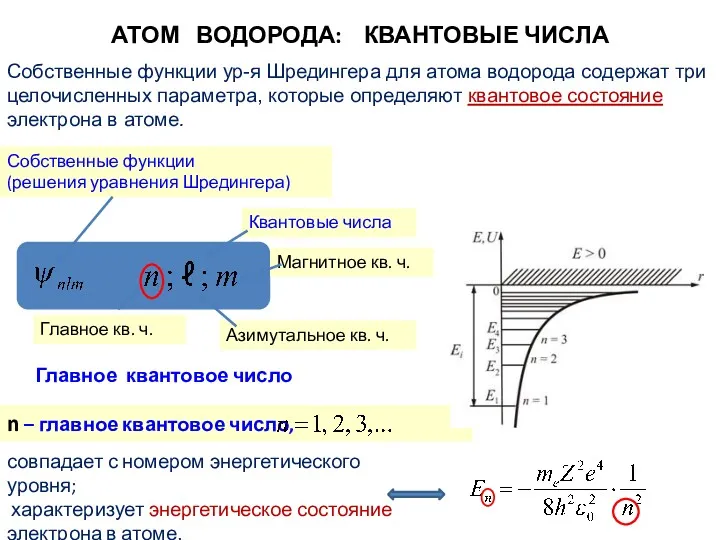
- 10. Собственные функции ур-я Шредингера для атома водорода содержат три целочисленных параметра, которые определяют квантовое состояние электрона
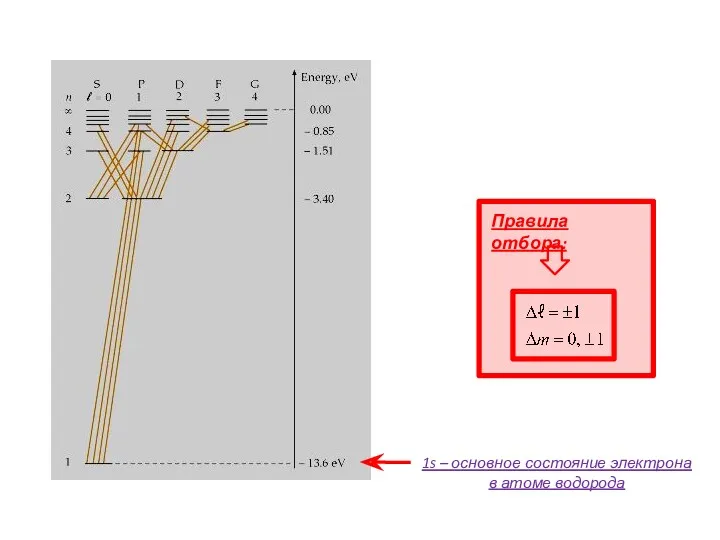
- 11. АТОМ ВОДОРОДА: КВАНТОВЫЕ ЧИСЛА Азимутальное квантовое число Величина момента импульса квантована (!) В отличие от модели
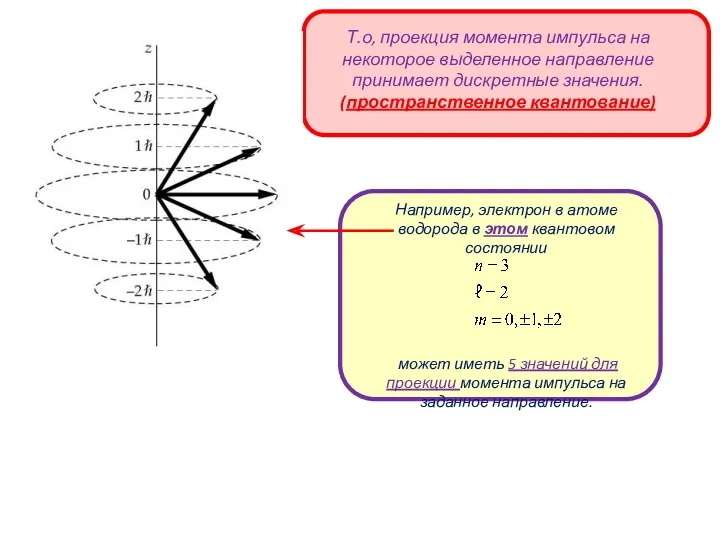
- 12. АТОМ ВОДОРОДА: КВАНТОВЫЕ ЧИСЛА Магнитное квантовое число Т.е. проекция момента импульса на некоторое выделенное направление принимает
- 13. m – магнитное квантовое число Одному энергетическому состоянию может соответствовать несколько квантовых состояний электрона – вырожденные
- 14. 1 4 9 АТОМ ВОДОРОДА: РАЗЛИЧНЫЕ КВАНТОВЫЕ СОСТОЯНИЯ, ОРБИТАЛИ
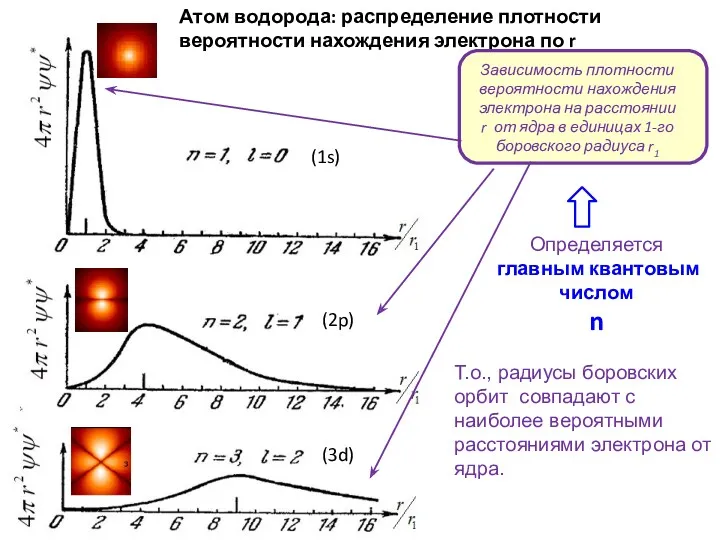
- 15. Атом водорода: распределение плотности вероятности нахождения электрона по r Т.о., радиусы боровских орбит совпадают с наиболее
- 16. Опыты Штерна и Герлаха. Пространственное квантование. Открытие спина электрона. 1922 г.
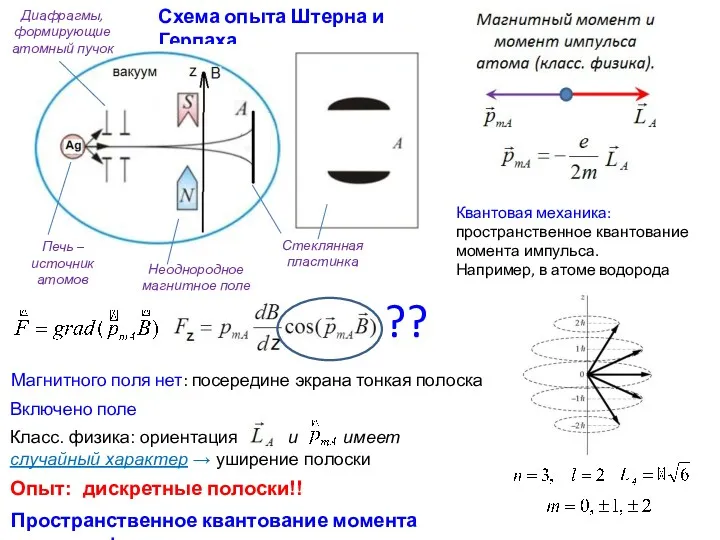
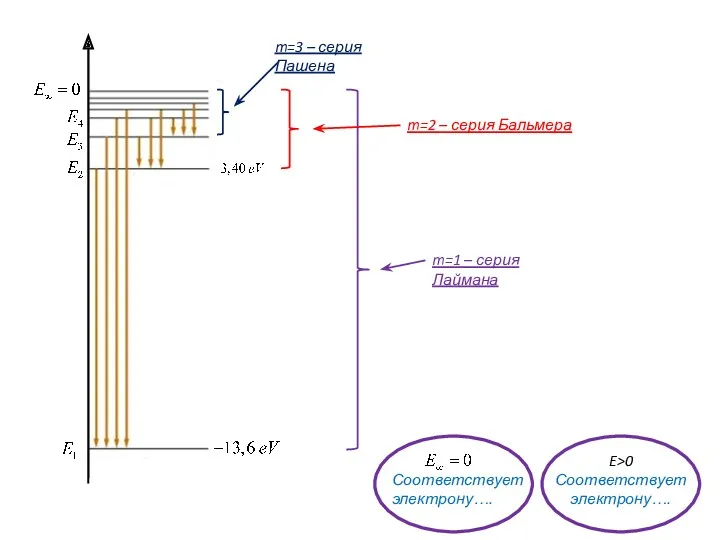
- 17. Схема опыта Штерна и Герлаха Квантовая механика: пространственное квантование момента импульса. Например, в атоме водорода ??
- 18. Собственный магнитный момент электрона - спин При отсутствии у атома магнитного момента (щелочные металлы, Ag) в
- 19. Первое начало термодинамики. Теплоёмкость идеального газа. Уравнение Майера. Работа, совершаемая идеальным газом, при различных физических процессах
- 20. Волновая функция. Уравнение Шредингера. Стационарное уравнение Шредингера. Физический смысл и свойства волновой функции. Микрочастица в бесконечно
- 22. Распределение электронов по энергетическим уровням в многоэлектронных атомах. Принцип Паули. 1) Квантовое состояние каждого электрона в
- 23. ЭЛЕКТРОННАЯ ОБОЛОЧКА -совокупность электронов в атоме, состояния которых характеризуются определёнными гл. квантовым числом n и орбитальным
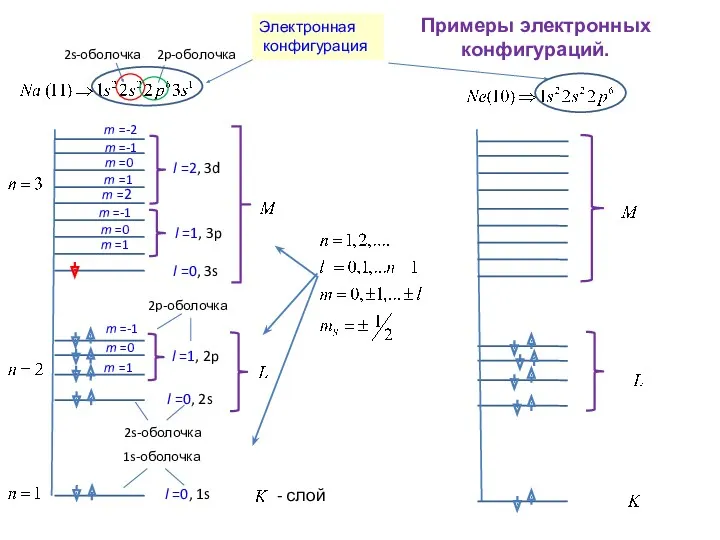
- 24. Примеры электронных конфигураций. 2p-оболочка 2s-оболочка l =0, 2s Электронная конфигурация 2s-оболочка
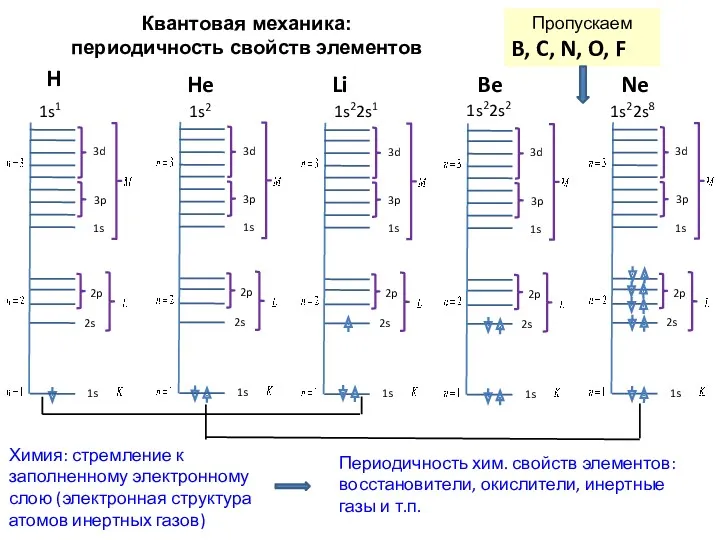
- 25. Квантовая механика: периодичность свойств элементов H He Li Be 1s1 1s2 1s22s1 1s22s2 Пропускаем B, C,
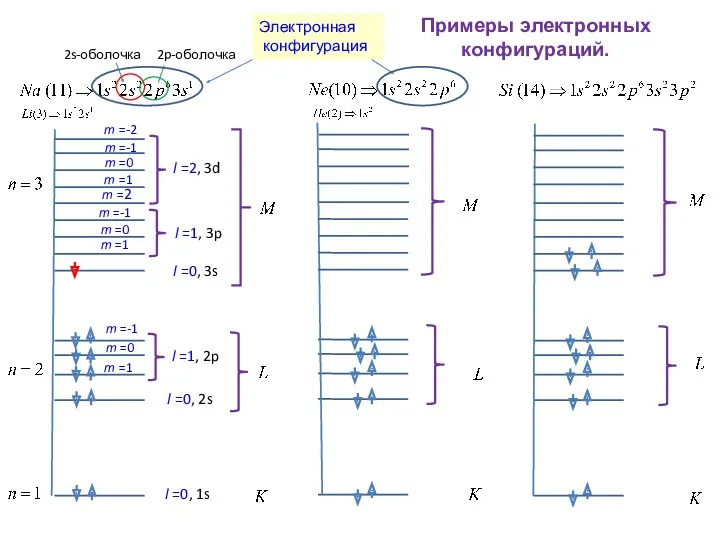
- 26. Примеры электронных конфигураций. 2p-оболочка 2s-оболочка l =1, 2p l =0, 2s l =1, 3p l =0,
- 28. Самостоятельно: ВСЁ, ЧТО БЫЛО УКАЗАНО В ЛЕКЦИЯХ : Закон зеркального отражения (самостоятельно) Зеркала Френеля Бипризма Френеля
- 29. Данному n соответствует состояний, в которых могут находится не более электронов (в слое). Для полностью заполненной
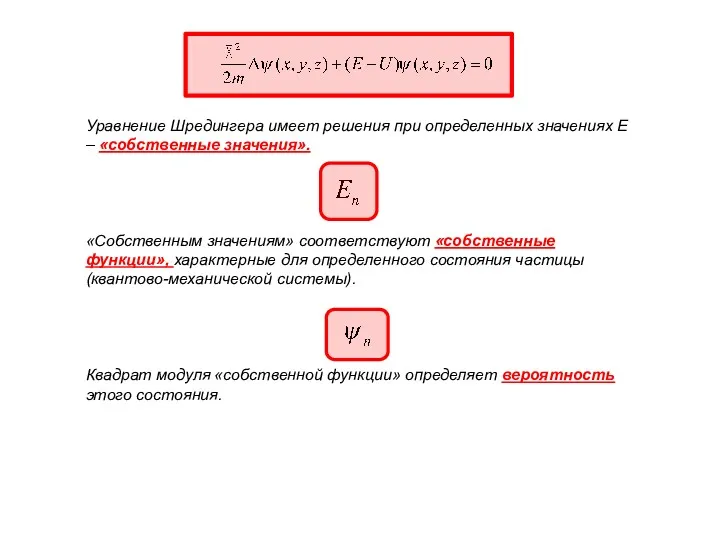
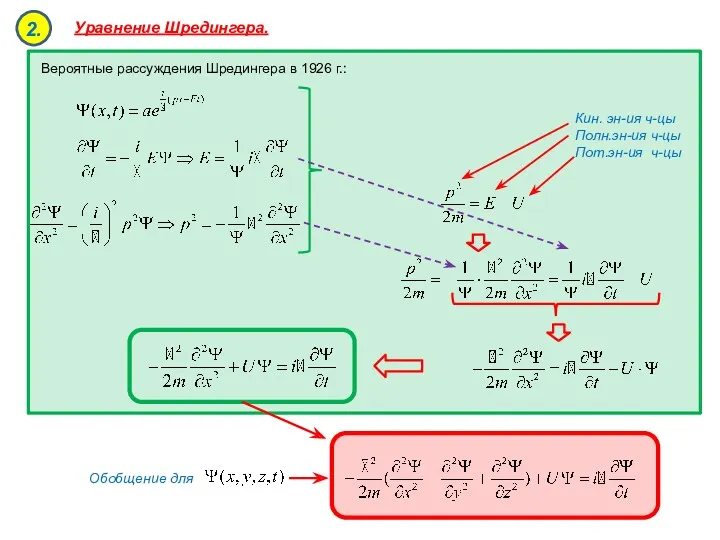
- 37. Стационарное уравнение Шредингера. Если силовое поле, в котором движется частица, стационарно, т.е. не зависит от времени,
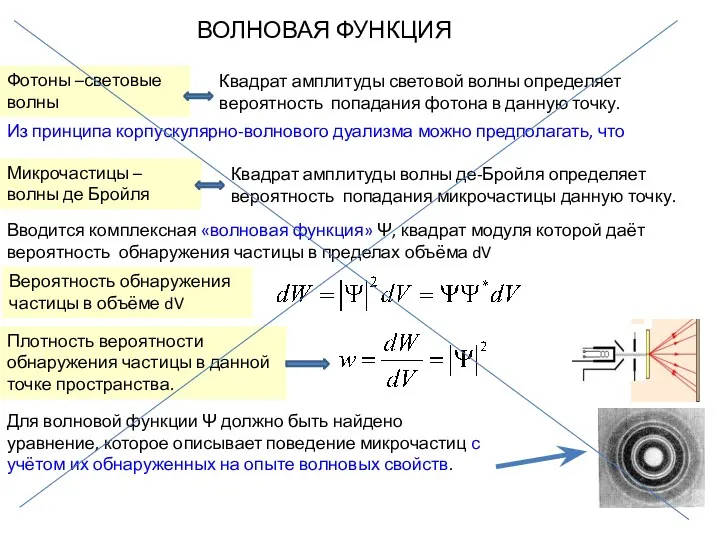
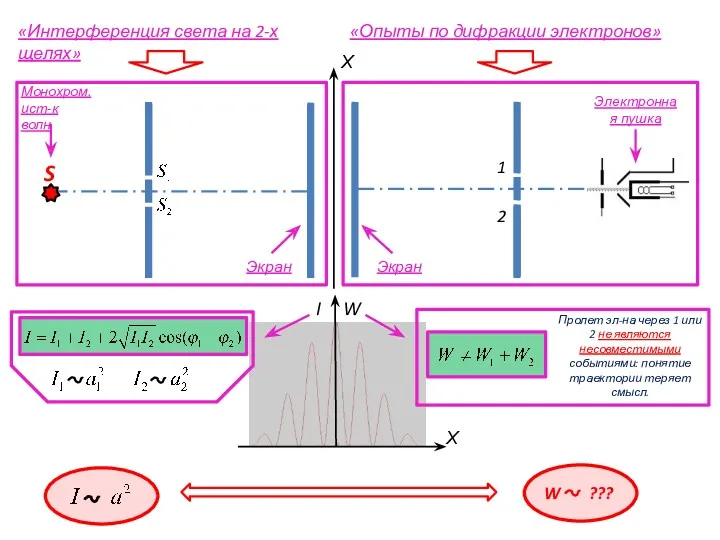
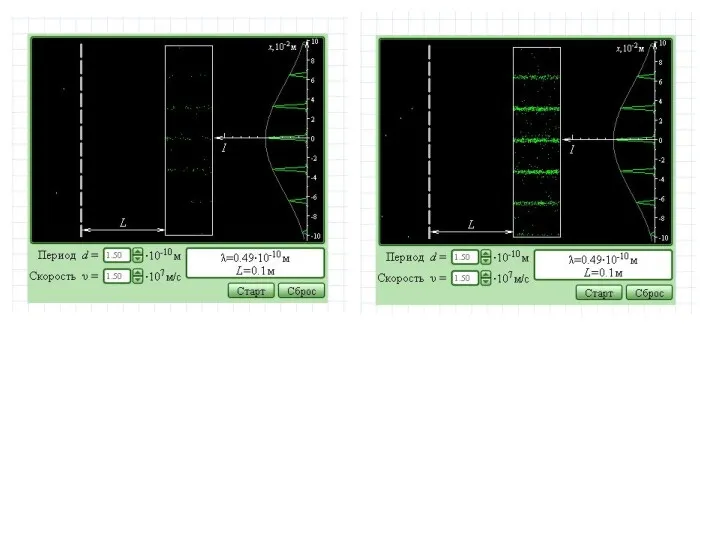
- 39. ВОЛНОВАЯ ФУНКЦИЯ Фотоны –световые волны Квадрат амплитуды световой волны определяет вероятность попадания фотона в данную точку.
- 40. Вопросы Микрочастицы обладают свойствами корпускулярности: масса, размеры, заряд неделимы. Но заряд то в атоме размазан –
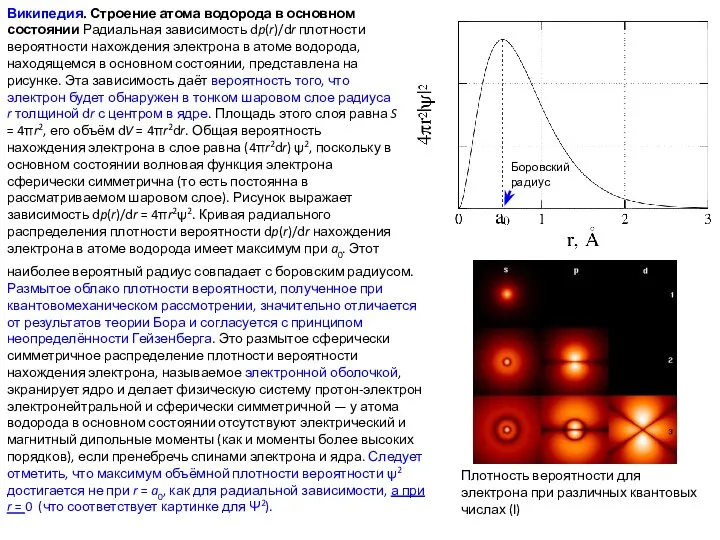
- 41. Википедия. Строение атома водорода в основном состоянии Радиальная зависимость dp(r)/dr плотности вероятности нахождения электрона в атоме
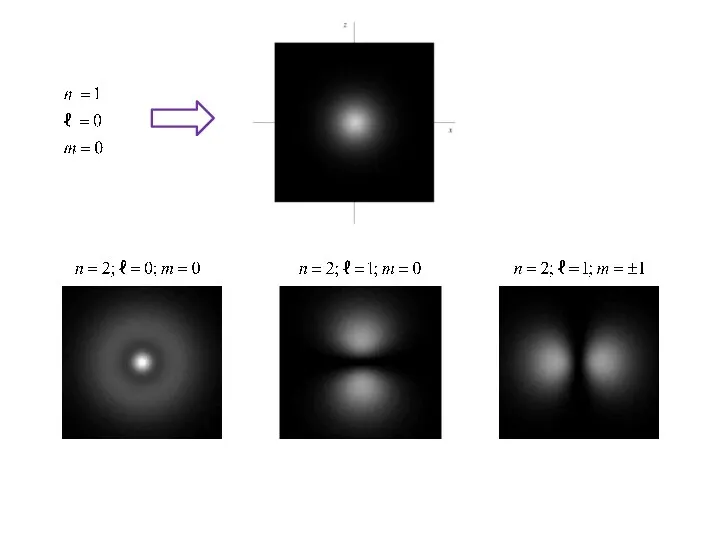
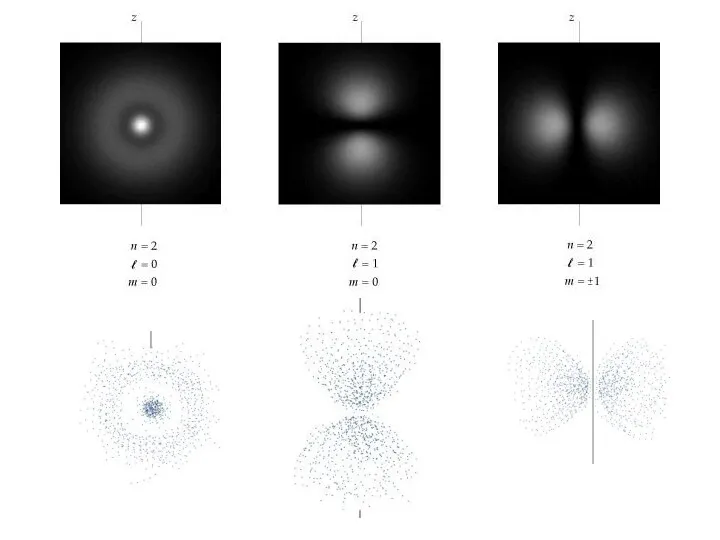
- 42. Визуализация орбиталей атома водорода Изображение справа показывает первые несколько орбиталей атома водорода (собственные функции гамильтониана). Они
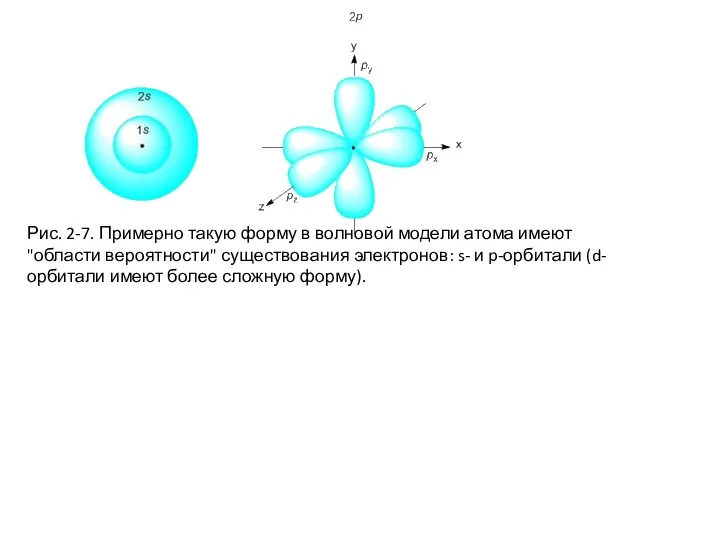
- 43. Рис. 2-7. Примерно такую форму в волновой модели атома имеют "области вероятности" существования электронов: s- и
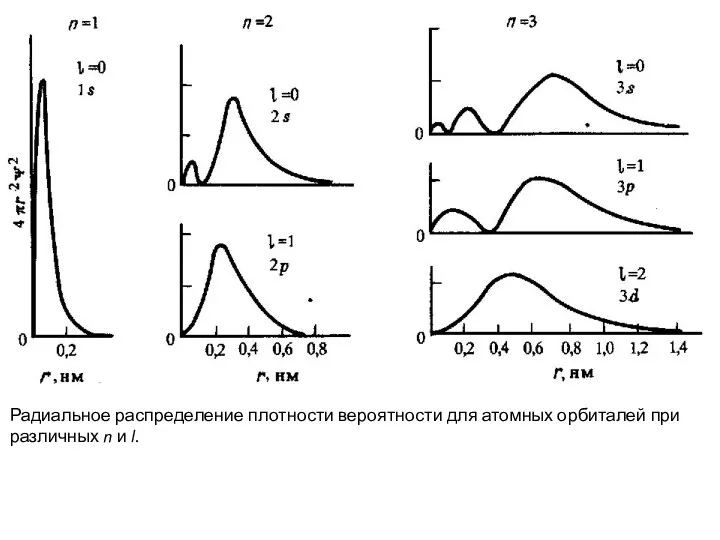
- 44. Радиальное распределение плотности вероятности для атомных орбиталей при различных n и l.
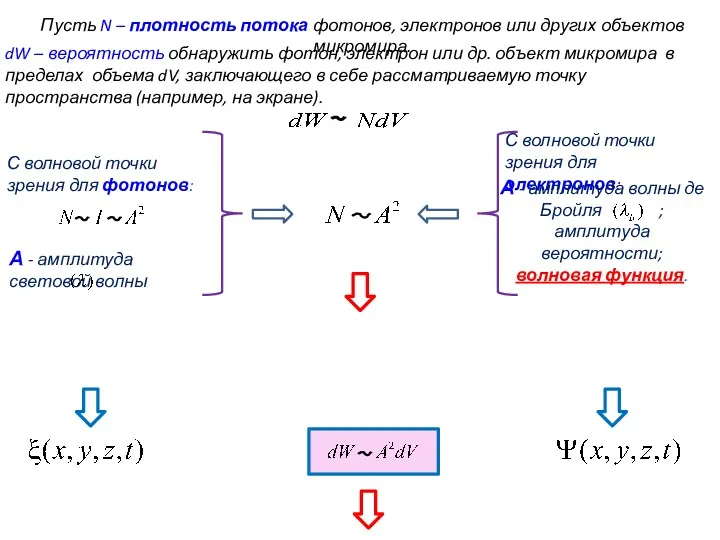
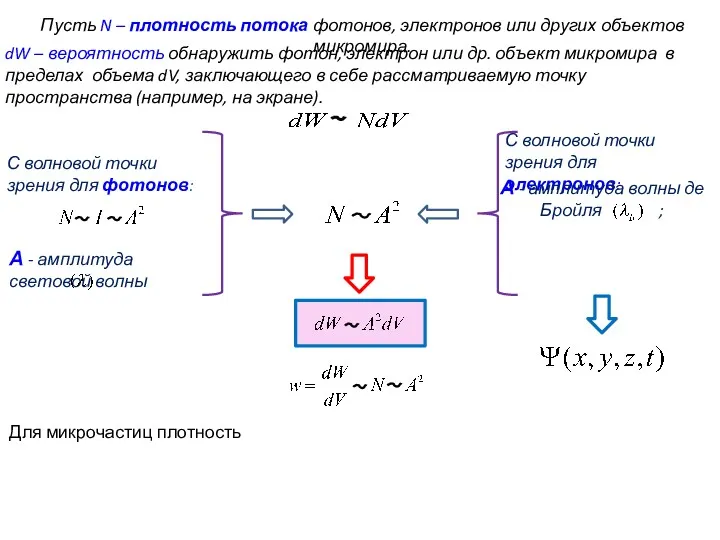
- 45. Пусть N – плотность потока фотонов, электронов или других объектов микромира. dW – вероятность обнаружить фотон,
- 46. Пусть N – плотность потока фотонов, электронов или других объектов микромира. dW – вероятность обнаружить фотон,
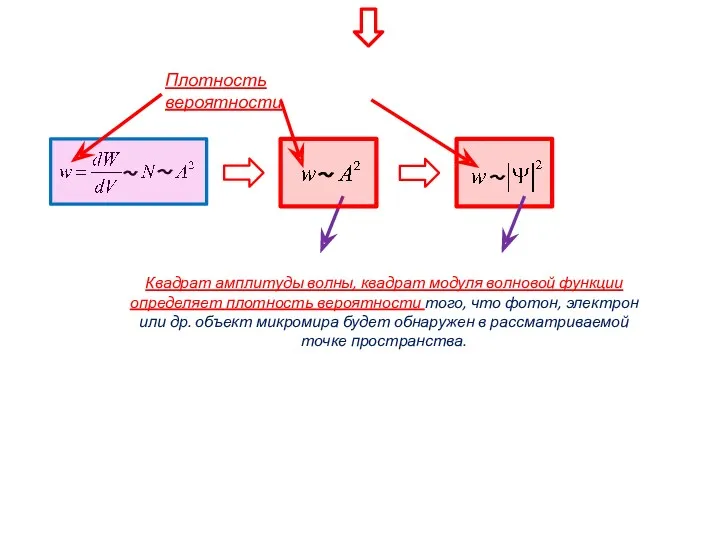
- 47. Плотность вероятности Квадрат амплитуды волны, квадрат модуля волновой функции определяет плотность вероятности того, что фотон, электрон
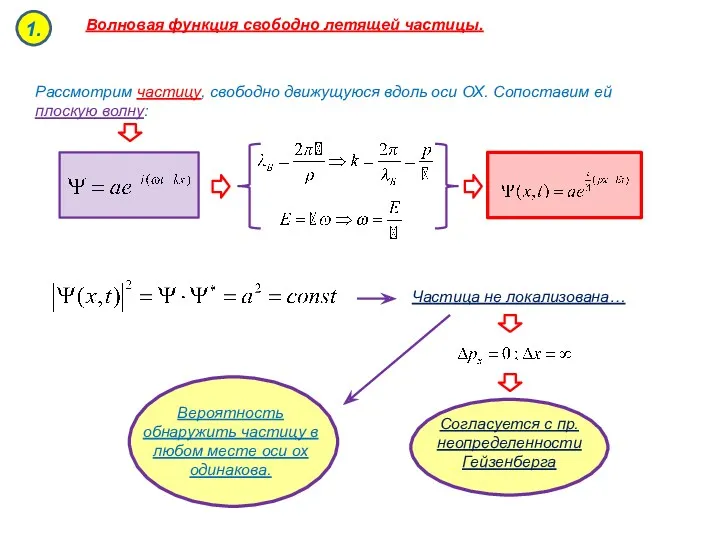
- 52. Волновая функция свободно летящей частицы. Частица не локализована… Вероятность обнаружить частицу в любом месте оси ох
- 54. Должен ли диполь (магнитный или электрический) ориентироваться по полю? Пусть макроскопический диполь (постоянный магнит) с дипольным
- 56. Скачать презентацию























 Продольные и поперечные магнитооптические эффекты
Продольные и поперечные магнитооптические эффекты AGCS (Active Geometry Controlled Suspension) - активная управляемая геометрия подвески
AGCS (Active Geometry Controlled Suspension) - активная управляемая геометрия подвески Оптические методы
Оптические методы Көлікті пайдалану және жүк қозғалысы мен тасымалдауды ұйымдастыру
Көлікті пайдалану және жүк қозғалысы мен тасымалдауды ұйымдастыру Электрическая цепь и ее составные части
Электрическая цепь и ее составные части Видимое излучение
Видимое излучение Равномерное прямолинейное движение. Равноускоренное движение. Ускорение. Инерциальные системы отчета
Равномерное прямолинейное движение. Равноускоренное движение. Ускорение. Инерциальные системы отчета Метрология как наука. Её значение, цель, задачи, функции
Метрология как наука. Её значение, цель, задачи, функции Кинематика точки
Кинематика точки Геометрическая оптика. 11 класс
Геометрическая оптика. 11 класс МЭМС и НЭМС: электронные системы, жидкостные вентили, насосы и биомедицинские системы
МЭМС и НЭМС: электронные системы, жидкостные вентили, насосы и биомедицинские системы 8кл. Повторение по теме Электричество
8кл. Повторение по теме Электричество Оптика
Оптика Электромагнитные волны
Электромагнитные волны Свободное падение тел. 9 класс
Свободное падение тел. 9 класс Детали машин и основы конструирования. Цепные передачи. (Лекция 6)
Детали машин и основы конструирования. Цепные передачи. (Лекция 6) Теорема Гаусса для вектора магнитной индукции
Теорема Гаусса для вектора магнитной индукции Строение глаза. Влияние свойств зрения на точность измерений. Продольное наведение. Поперечное наведение
Строение глаза. Влияние свойств зрения на точность измерений. Продольное наведение. Поперечное наведение Критичность ограниченных размножающих сред
Критичность ограниченных размножающих сред Урок Электрические явления с элементами здоровьесберегающей технологии и экологической направленностью.
Урок Электрические явления с элементами здоровьесберегающей технологии и экологической направленностью. Уравнение динамики идеальной сплошной среды. Модель линий ток. Уравнение динамики при возмущении среды
Уравнение динамики идеальной сплошной среды. Модель линий ток. Уравнение динамики при возмущении среды Сложное движение твердого тела
Сложное движение твердого тела Механическая энергия. Кинетическая и потенциальная энергия. Закон сохранения энергии
Механическая энергия. Кинетическая и потенциальная энергия. Закон сохранения энергии Квантовые системы. Распределение электронов в атоме. Квантовые числа. Принцип Паули. Спонтанное и вынужденное излучение. Лазеры
Квантовые системы. Распределение электронов в атоме. Квантовые числа. Принцип Паули. Спонтанное и вынужденное излучение. Лазеры Магниты. 11 класс
Магниты. 11 класс Сила Архимеда
Сила Архимеда Этапы развития ускорителей. Методы ускорения. Магнитная система ускорителей. Источники частиц. Синхротронное излучение
Этапы развития ускорителей. Методы ускорения. Магнитная система ускорителей. Источники частиц. Синхротронное излучение Механическая работа
Механическая работа