Содержание
- 2. Программа регулирования План формирования задающего воздействия g(t) на систему. временной: y=y(t); параметрический: y=y(s1,s2,s3,…,sn).
- 3. Законы регулирования Линейные непрерывные. Нелинейные.
- 4. Классификация нелинейных законов регулирования Функциональные. Логические. Параметрические. Оптимизирующие. Если |x| 0.2Gm, тогда u=k2x; где: k1 u=k(t[°C];h[м];G[кг])x.
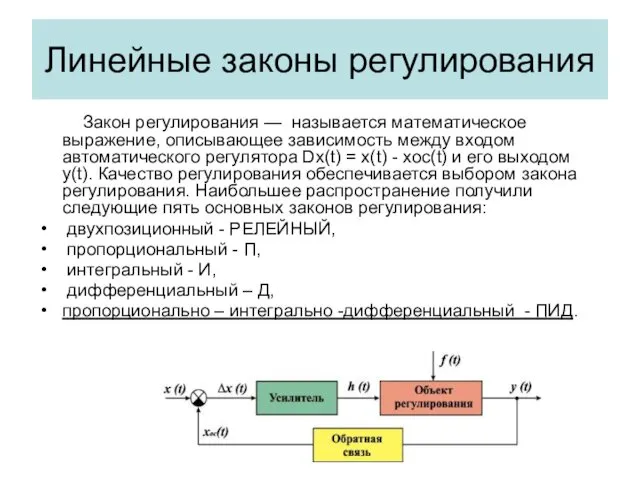
- 5. Линейные законы регулирования Закон регулирования — называется математическое выражение, описывающее зависимость между входом автоматического регулятора Dx(t)
- 6. Двухпозиционный регулятор В режиме двухпозиционного регулятора логическое устройство (компаратор) сравнивает значение входной величины с заданием и
- 7. Применение двухпозиционного регулятора Для регулирования измеряемой величины в несложных системах, когда не требуется точности поддержания регулируемой
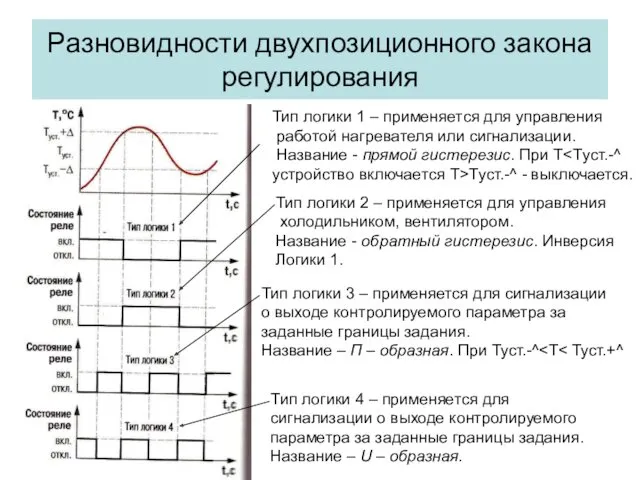
- 8. Разновидности двухпозиционного закона регулирования Тип логики 1 – применяется для управления работой нагревателя или сигнализации. Название
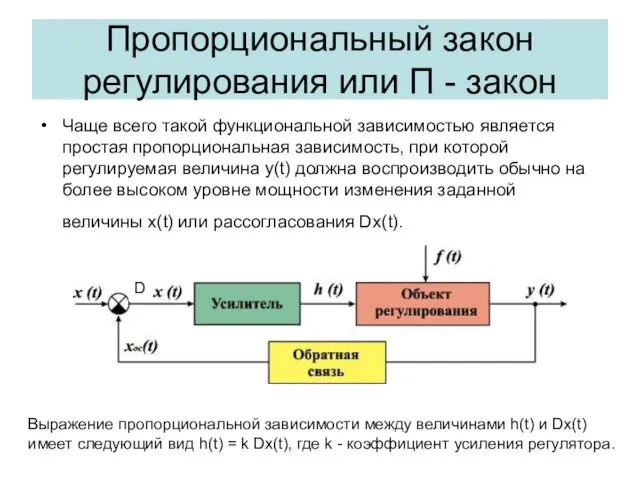
- 9. Пропорциональный закон регулирования или П - закон Чаще всего такой функциональной зависимостью является простая пропорциональная зависимость,
- 10. Свойства системы с П - регулятором Достоинство – отсутствие инерционности: реакция П - регулятора на изменение
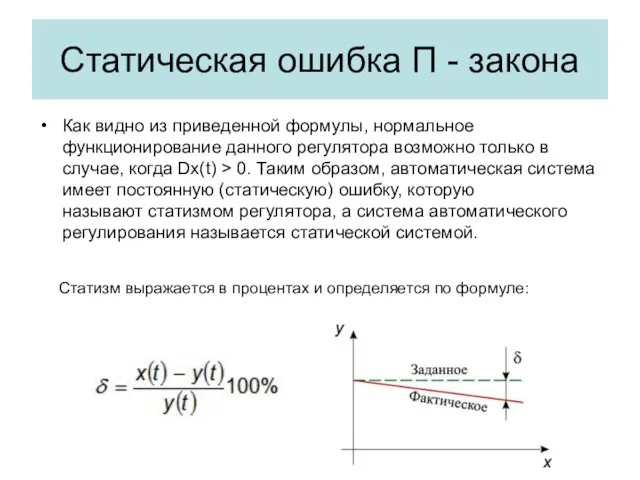
- 11. Статическая ошибка П - закона Как видно из приведенной формулы, нормальное функционирование данного регулятора возможно только
- 12. Линейные алгоритмы управления Алгоритмы управления для устройств пропорционального типа (например – управление нагревателем электропечи). Алгоритмы управления
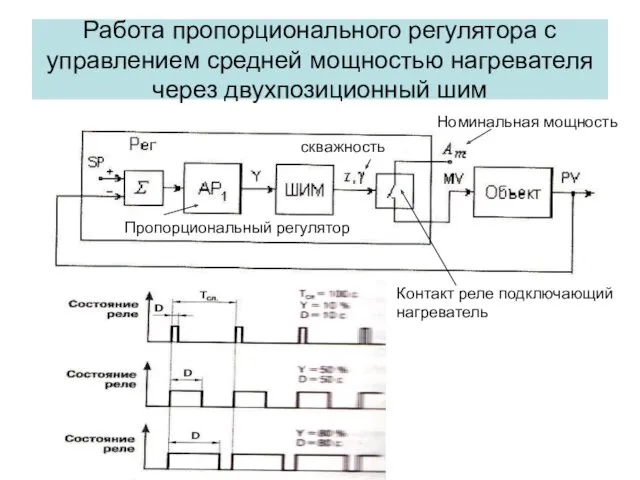
- 13. Работа пропорционального регулятора с управлением средней мощностью нагревателя через двухпозиционный шим Номинальная мощность скважность Пропорциональный регулятор
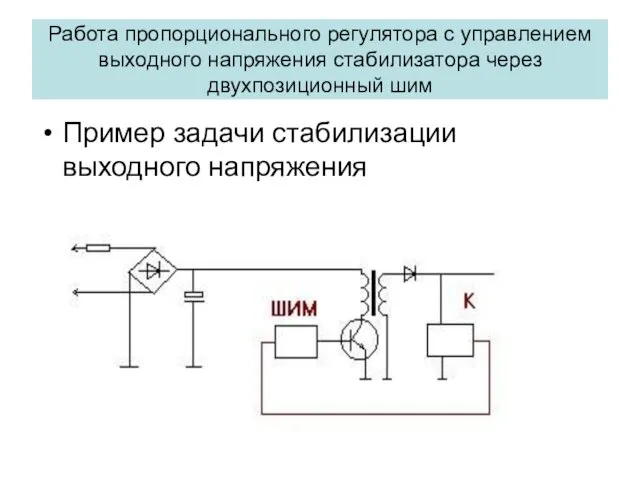
- 14. Пример задачи стабилизации выходного напряжения Работа пропорционального регулятора с управлением выходного напряжения стабилизатора через двухпозиционный шим
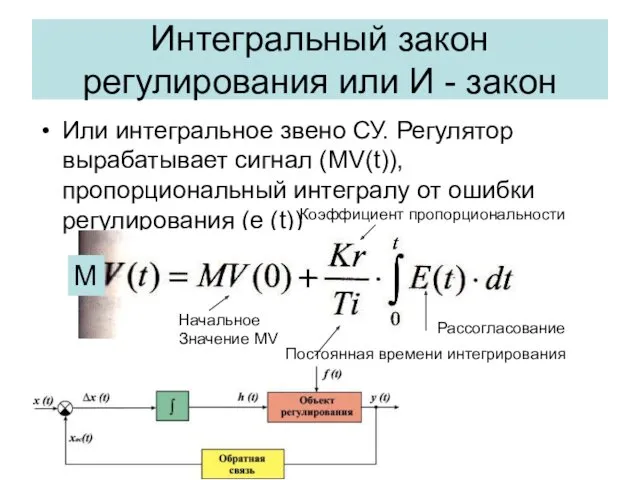
- 15. Интегральный закон регулирования или И - закон Или интегральное звено СУ. Регулятор вырабатывает сигнал (MV(t)), пропорциональный
- 16. Свойство системы с интегральным регулятором Достоинством И - регулятора является отсутствие ошибки регулирования в установившемся режиме.
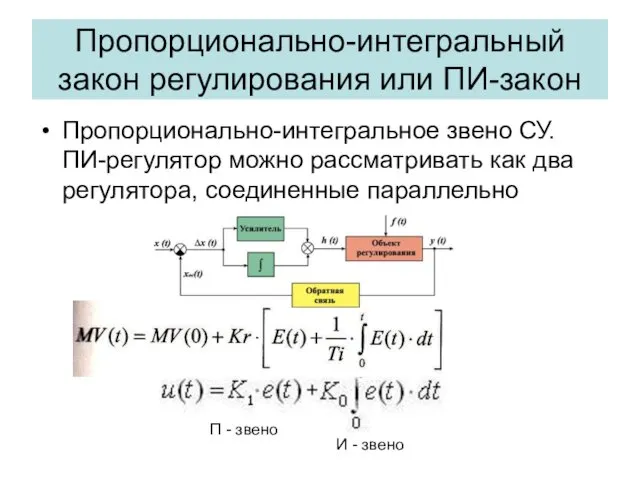
- 17. Пропорционально-интегральный закон регулирования или ПИ-закон Пропорционально-интегральное звено СУ. ПИ-регулятор можно рассматривать как два регулятора, соединенные параллельно
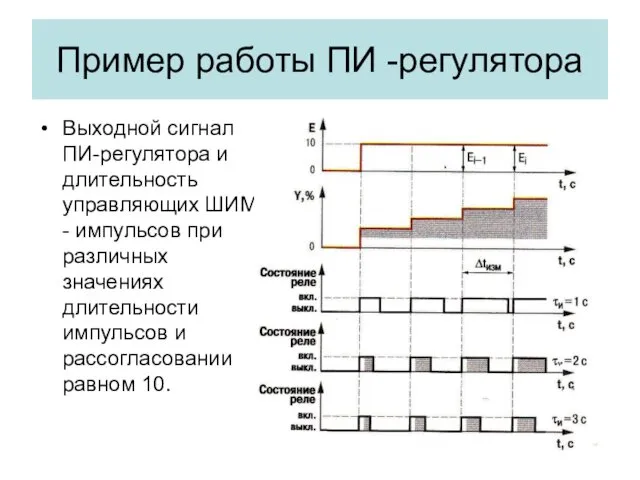
- 18. Пример работы ПИ -регулятора Выходной сигнал ПИ-регулятора и длительность управляющих ШИМ - импульсов при различных значениях
- 19. Свойства системы с ПИ-регулятором Применение ПИ закона регулирования позволяет сочетать в одном устройстве положительные свойства П
- 20. Настройка ПИ регулятора Для настройки ПИ регулятора следует сначала установить постоянную времени интегрирования равный нулю, а
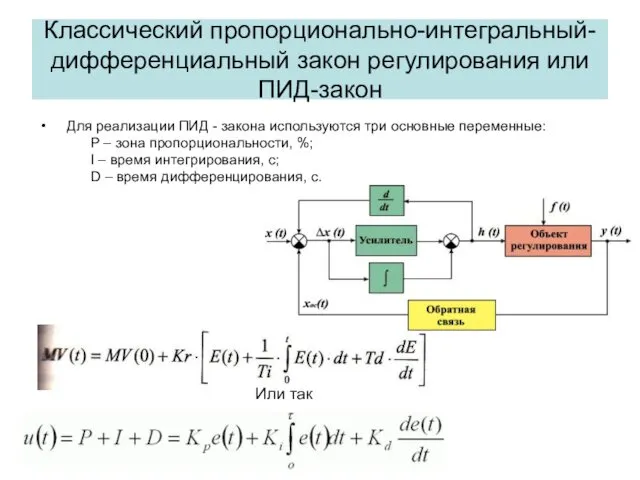
- 21. Классический пропорционально-интегральный-дифференциальный закон регулирования или ПИД-закон Для реализации ПИД - закона используются три основные переменные: P
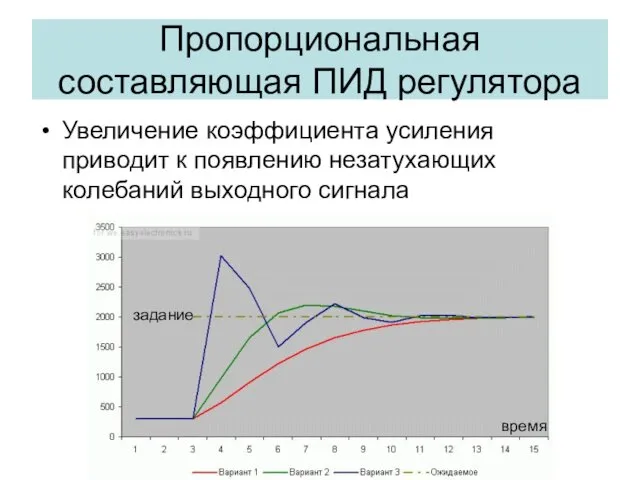
- 22. Пропорциональная составляющая ПИД регулятора Увеличение коэффициента усиления приводит к появлению незатухающих колебаний выходного сигнала задание время
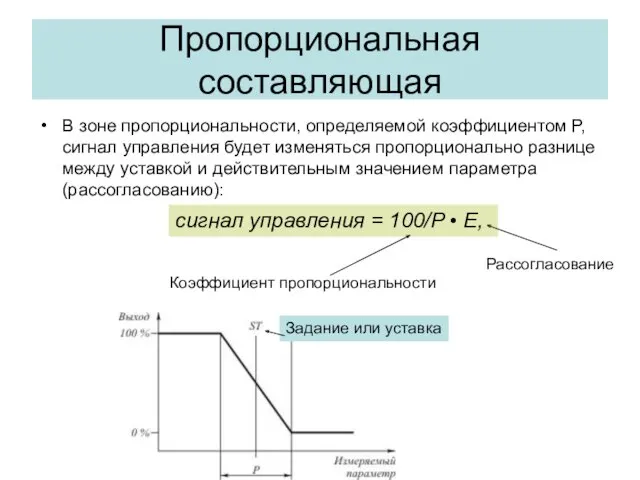
- 23. Пропорциональная составляющая В зоне пропорциональности, определяемой коэффициентом Р, сигнал управления будет изменяться пропорционально разнице между уставкой
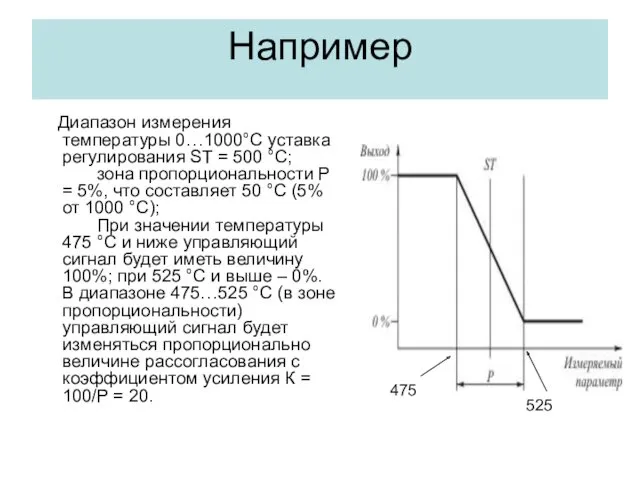
- 24. Например Диапазон измерения температуры 0…1000°С уставка регулирования ST = 500 °С; зона пропорциональности P = 5%,
- 25. Важно Уменьшение значения зоны пропорциональности Р увеличивает реакцию регулятора на рассогласование, т. е. малому рассогласованию будет
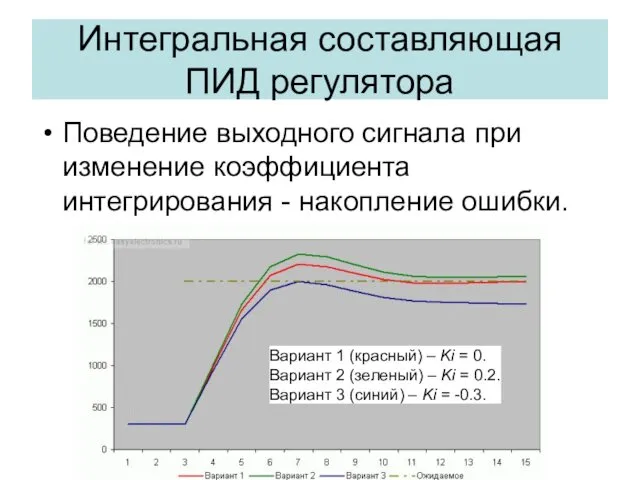
- 26. Интегральная составляющая ПИД регулятора Поведение выходного сигнала при изменение коэффициента интегрирования - накопление ошибки. Вариант 1
- 27. Интегральная составляющая Определяется постоянной времени интегрирования I, является функцией времени и обеспечивает изменение коэффициента усиления (сдвиг
- 28. Дифференциальная составляющая Многие объекты регулирования достаточно инерционны, т. е. имеют задержку реакции на приложенное воздействие (мертвое
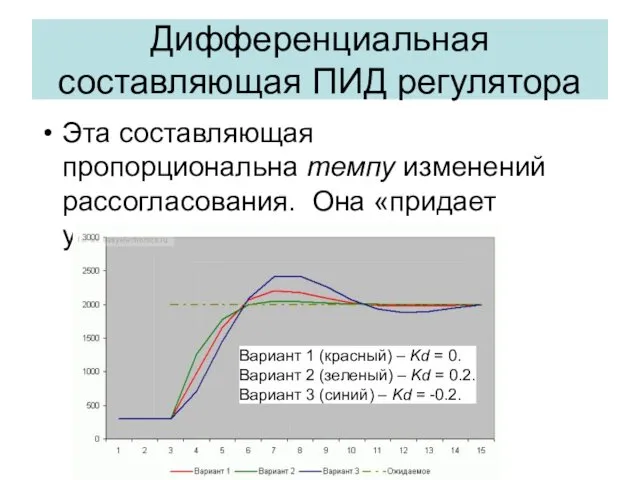
- 29. Дифференциальная составляющая ПИД регулятора Эта составляющая пропорциональна темпу изменений рассогласования. Она «придает ускорение». Вариант 1 (красный)
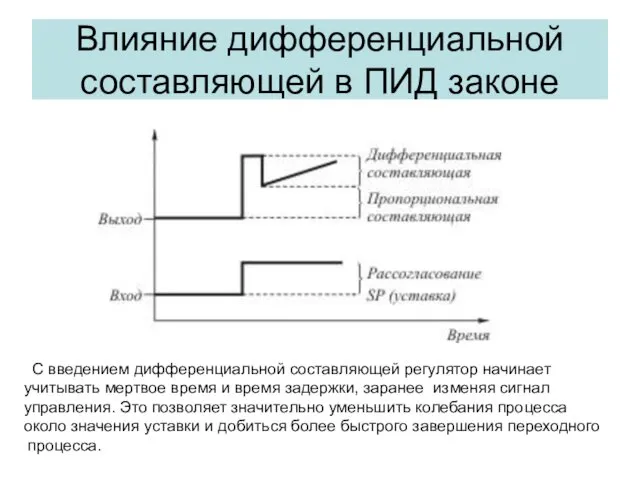
- 30. Влияние дифференциальной составляющей в ПИД законе С введением дифференциальной составляющей регулятор начинает учитывать мертвое время и
- 31. Свойства системы с ПИД-регулятором ПИД - закон является наиболее совершенным из общепромышленных алгоритмов регулирования с точки
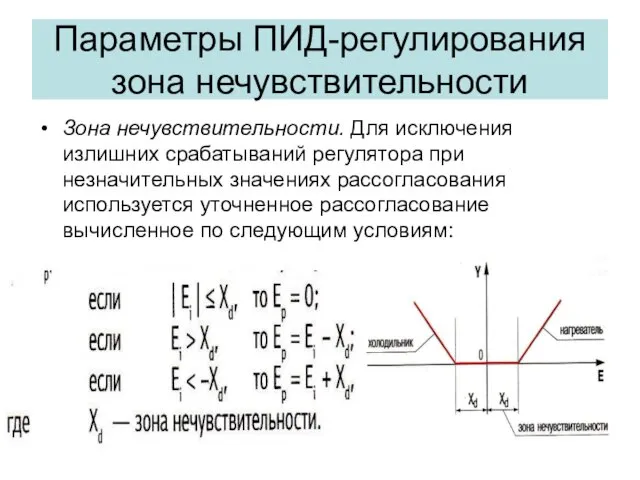
- 32. Параметры ПИД-регулирования зона нечувствительности Зона нечувствительности. Для исключения излишних срабатываний регулятора при незначительных значениях рассогласования используется
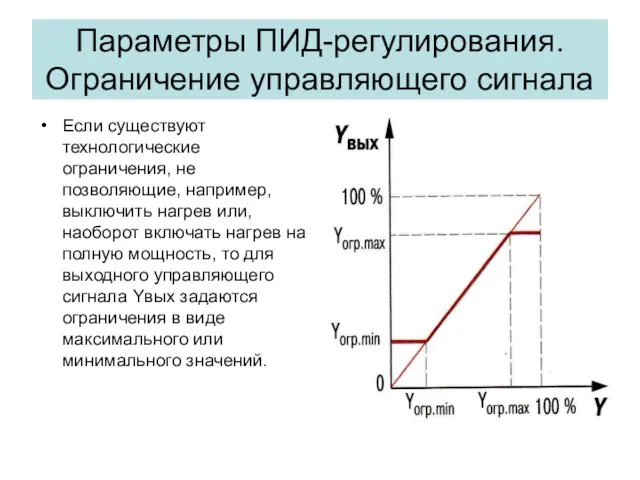
- 33. Параметры ПИД-регулирования. Ограничение управляющего сигнала Если существуют технологические ограничения, не позволяющие, например, выключить нагрев или, наоборот
- 34. Немного математики u (t) — наша Функция; P — пропорциональная составляющая; I — интегральная составляющая; D
- 35. ПИД закон Дискретная реализация формулы на основе численных методов: u(t) = P (t) + I (t)
- 36. Настройка ПИД - регулятора Увеличение пропорционального коэффициента увеличивает быстродействие и снижает запас устойчивости; С уменьшением интегральной
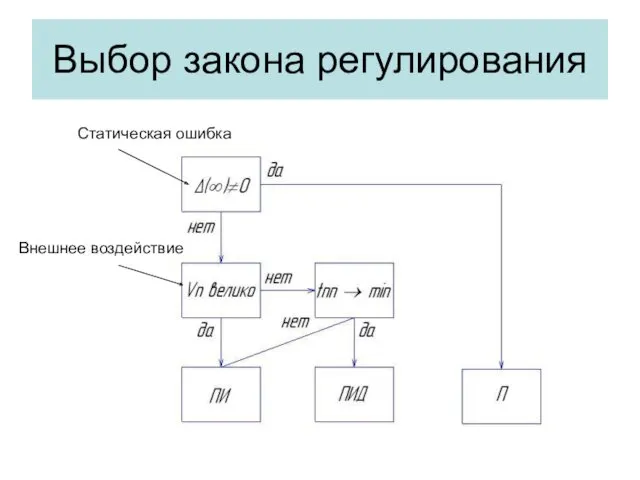
- 37. Выбор закона регулирования Статическая ошибка Внешнее воздействие
- 38. Первый шаг выбора регулятора Итак, в первую очередь, необходимо оценить, важно ли нам получить в результате
- 39. Второй шаг выбора закона регулирования Если же нам очень важно получить нулевую статическую ошибку, переходим по
- 40. Третий шаг выбора закона регулирования В случаи, если влияние внешних возмущений велико, то «оптимальным» алгоритмом будет
- 41. Четвертый шаг Если же влияние возмущений несущественное – переходим по стрелке вправо и оцениваем ещё один
- 42. Пятый шаг Насколько важно время переходного процесса? Если время переходного процесса для вас не существенно, а
- 44. Скачать презентацию






















 Презентация к уроку: Подвижная карта звездного неба, 9 класс
Презентация к уроку: Подвижная карта звездного неба, 9 класс Трактори та мінітрактори, які використовуються у лісовому господарстві. Лекція 1. Частина 2
Трактори та мінітрактори, які використовуються у лісовому господарстві. Лекція 1. Частина 2 Давление твердых тел, жидкостей и газов. Урок физики. 7 класс
Давление твердых тел, жидкостей и газов. Урок физики. 7 класс урок презентация по физике в 7 классе
урок презентация по физике в 7 классе Физика плазмы
Физика плазмы 7класс. Простые механизмы ( моя презентация)
7класс. Простые механизмы ( моя презентация) законы постоянного тока
законы постоянного тока Дифференциальная геометрия
Дифференциальная геометрия Испытания на сдвиг, методы определения модулей сдвига при кручении плоских образцов и пластин по периоду крутильных колебаний
Испытания на сдвиг, методы определения модулей сдвига при кручении плоских образцов и пластин по периоду крутильных колебаний Метрология, стандартизация и сертификация
Метрология, стандартизация и сертификация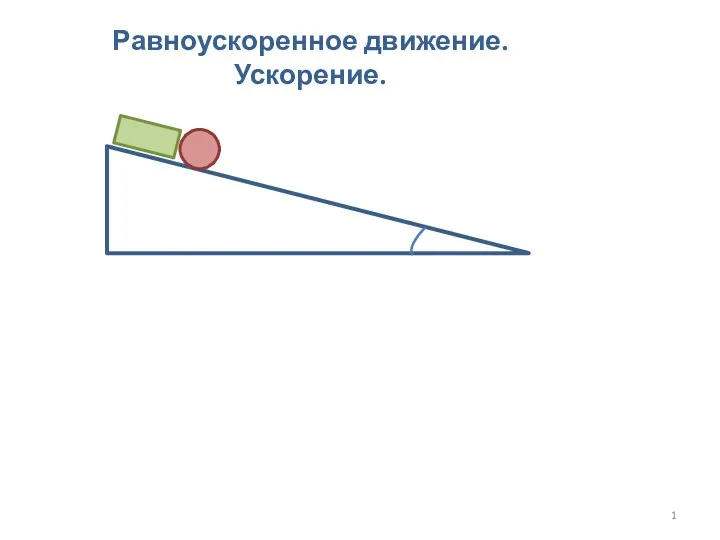 Равноускоренное движение. Ускорение
Равноускоренное движение. Ускорение Презентация к уроку 7 класса Агрегатные состояния вещества
Презентация к уроку 7 класса Агрегатные состояния вещества Эксперимент на уроках физики в основной школе как средство формирования УУД
Эксперимент на уроках физики в основной школе как средство формирования УУД Тесты по физике. Темы: Работа. Мощность. Энергия
Тесты по физике. Темы: Работа. Мощность. Энергия Отражение и преломление света. Закон преломления света. Полное отражение
Отражение и преломление света. Закон преломления света. Полное отражение Электрический ток в вакууме
Электрический ток в вакууме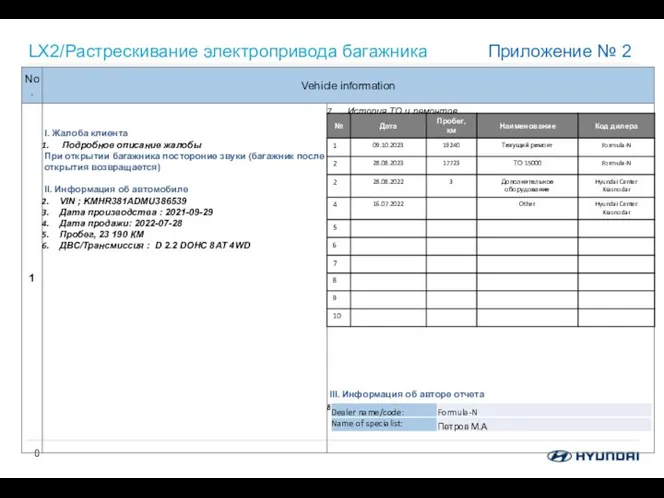 XWER381ADM0002070
XWER381ADM0002070 Своя игра по физике
Своя игра по физике Проектирование зоны ТО-1 грузовых автомобилей с выделением шиномонтажного участка, технологический процесс ремонта колес
Проектирование зоны ТО-1 грузовых автомобилей с выделением шиномонтажного участка, технологический процесс ремонта колес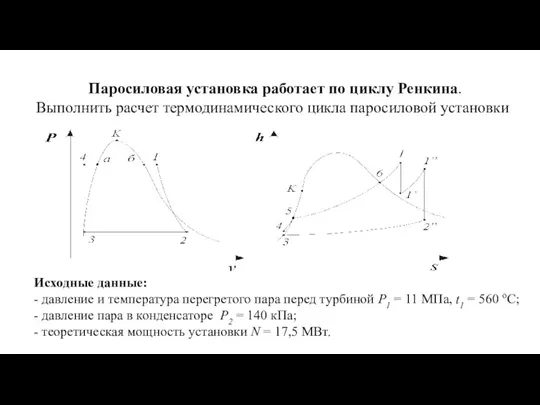 Расчет термодинамического цикла паросиловой установки
Расчет термодинамического цикла паросиловой установки Кинематика материальной точки
Кинематика материальной точки Домашняя лабораторная работа. Плотность куска мыла
Домашняя лабораторная работа. Плотность куска мыла Однородный полупроводник
Однородный полупроводник Рентгеновские аппараты. Цифровые рентгенодиагностические комплексы. (Лекция 10)
Рентгеновские аппараты. Цифровые рентгенодиагностические комплексы. (Лекция 10) Создание телефона
Создание телефона Оптические волокна
Оптические волокна Структура измерительных приборов и систем
Структура измерительных приборов и систем Оптика. Описание оптических систем. (Лекция 5)
Оптика. Описание оптических систем. (Лекция 5)