Содержание
- 2. Четырехугольники
- 3. Параллелограмм Параллелограмм-это четырёхугольник, у которого противоположные стороны попарно параллельны. А В С D ABCD-параллелограмм АВ║СD; ВС║АD
- 4. Свойства параллелограмма 1. В параллелограмме противоположные стороны равны и противоположные углы равны. А В С D
- 5. 2. Диагонали параллелограмма точкой пересечения делятся пополам. АВСD- параллелограмм АВ;СD- диагонали АО=СО ВО=DО А B C
- 6. Признаки параллелограмма 1. Если в четырёхугольнике две стороны равны и параллельны, то этот четырёхугольник – параллелограмм.
- 7. 2. Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёх угольник – параллелограмм. ABCD –
- 8. 3. Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырёхугольник параллелограмм. ABCD-четырёхугольник
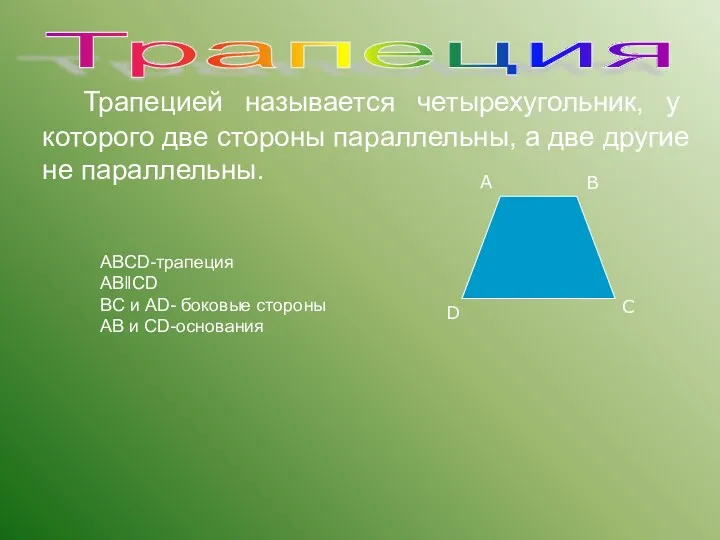
- 9. Трапецией называется четырехугольник, у которого две стороны параллельны, а две другие не параллельны. АВСD-трапеция АВ‖СD ВС
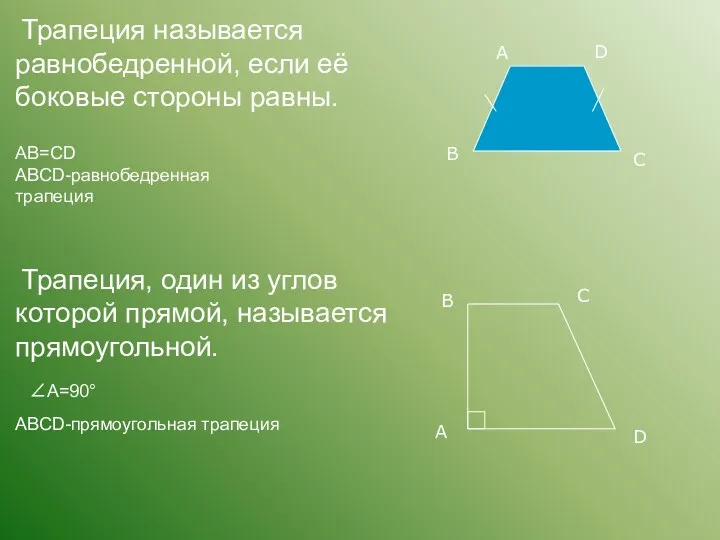
- 10. Трапеция называется равнобедренной, если её боковые стороны равны. АВ=СD АВСD-равнобедренная трапеция А В С D Трапеция,
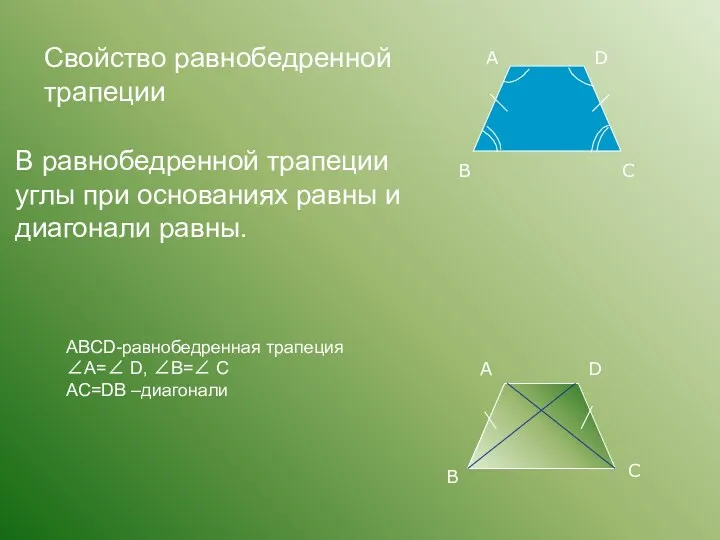
- 11. В равнобедренной трапеции углы при основаниях равны и диагонали равны. А В С D А D
- 12. Прямоугольником называется параллелограмм, у которого все углы прямые. А В С D Прямоугольник
- 13. Свойства прямоугольника
- 14. Прямоугольник обладает свойствами параллелограмма
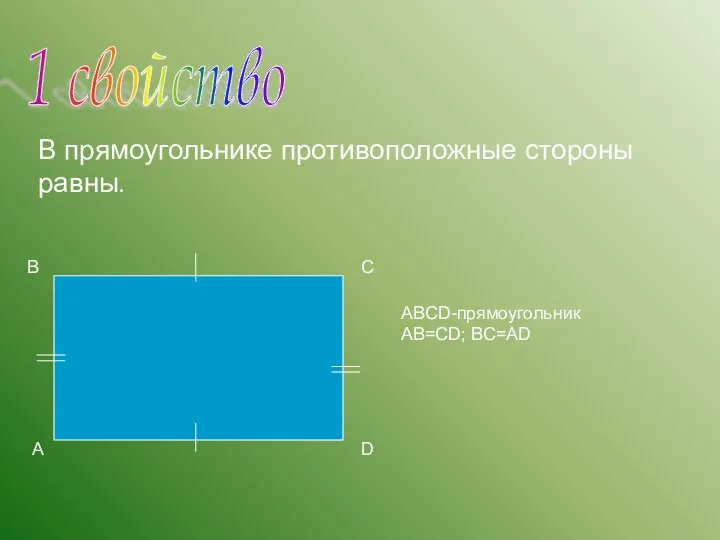
- 15. 1 свойство А В С D В прямоугольнике противоположные стороны равны. ABCD-прямоугольник АВ=СD; ВС=АD
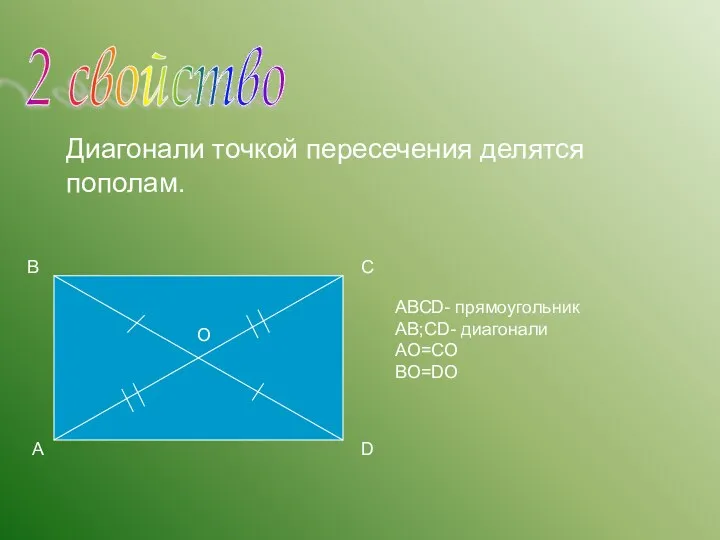
- 16. 2 свойство В А С D Диагонали точкой пересечения делятся пополам. О АВСD- прямоугольник АВ;СD- диагонали
- 17. Собственное свойство прямоугольника
- 18. Диагонали прямоугольника равны А В С D АВСD - прямоугольник АС, ВD – диагонали АС=ВD
- 19. Признак прямоугольника Если в параллелограмме диагонали равны, то этот параллелограмм - прямоугольник. А В С D
- 20. Ромб Ромбом называется параллелограмм, у которого все стороны равны. ABCD-ромб AB=BC=CD=AD A B C D
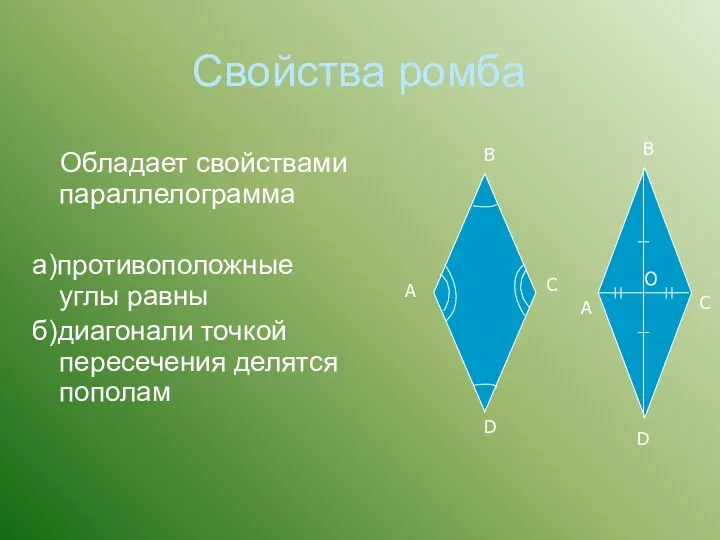
- 21. Свойства ромба Обладает свойствами параллелограмма а)противоположные углы равны б)диагонали точкой пересечения делятся пополам A B C
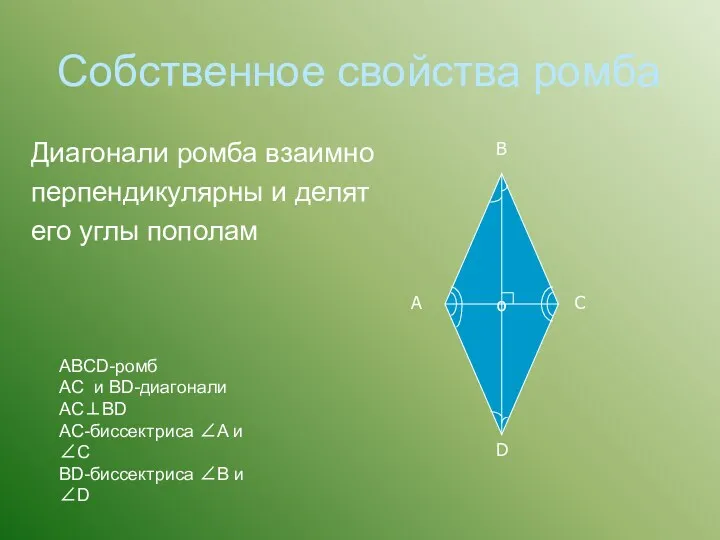
- 22. Собственное свойства ромба Диагонали ромба взаимно перпендикулярны и делят его углы пополам ABCD-ромб AC и BD-диагонали
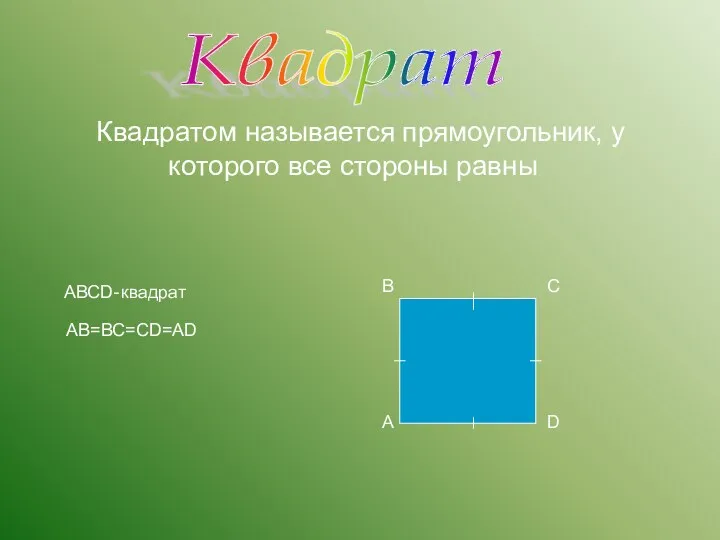
- 23. Квадратом называется прямоугольник, у которого все стороны равны В А С D АВСD- квадрат АВ=ВС=СD=АD Квадрат
- 24. Свойства квадрата Обладает свойствами прямоугольника и ромба: а) все углы прямые б) диагонали равны ,взаимно перпендикулярны
- 26. Скачать презентацию















 Открытый урок по математическому моделированию Идеальный каблук в рамках темы Подобие треугольников для 8 класса.
Открытый урок по математическому моделированию Идеальный каблук в рамках темы Подобие треугольников для 8 класса. Выступление на педагогических чтениях
Выступление на педагогических чтениях Применение электронных образовательных ресурсов в преподавании геометрии.
Применение электронных образовательных ресурсов в преподавании геометрии. Интеллектуальное казино, методическая разработка нестандартного урока по геометрии в 8 классе по теме Площади плоских фигур.
Интеллектуальное казино, методическая разработка нестандартного урока по геометрии в 8 классе по теме Площади плоских фигур. Cкалярное произведение векторов- презентация урока
Cкалярное произведение векторов- презентация урока Презентация Урок в 7 классе по теме Луч и угол
Презентация Урок в 7 классе по теме Луч и угол Урок геометрии в 7 классе по теме Сумма углов треугольника
Урок геометрии в 7 классе по теме Сумма углов треугольника 7класс Геометрия Второй признак равенства треугольников урок2
7класс Геометрия Второй признак равенства треугольников урок2 окружность.
окружность. Цилиндр
Цилиндр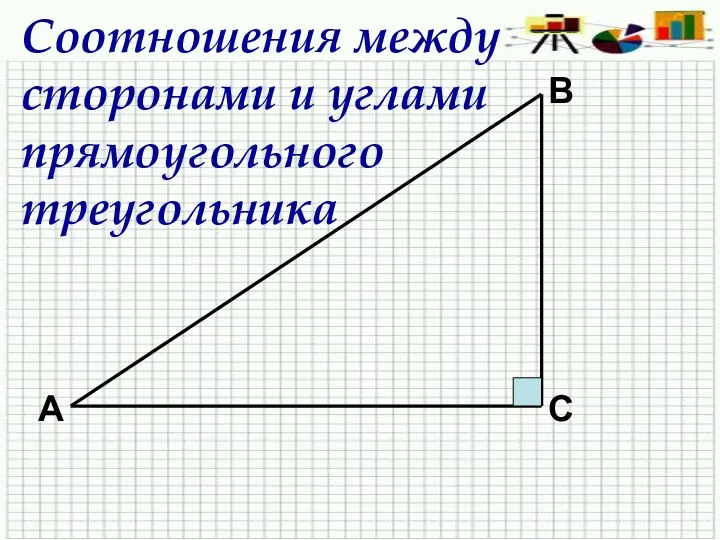 Соотношение между сторонами и углами прямоугольного треугольника.
Соотношение между сторонами и углами прямоугольного треугольника. презентация по теме Прямая и обратная теорема
презентация по теме Прямая и обратная теорема Математический диктант по теме Конус. Цилиндр
Математический диктант по теме Конус. Цилиндр Введение. Предмет геометрии. Аксиомы геометрии. Параллельные прямые в пространстве. Параллельность прямой и плоскости. Решение задач по теме: Параллельность прямой и плоскости.
Введение. Предмет геометрии. Аксиомы геометрии. Параллельные прямые в пространстве. Параллельность прямой и плоскости. Решение задач по теме: Параллельность прямой и плоскости.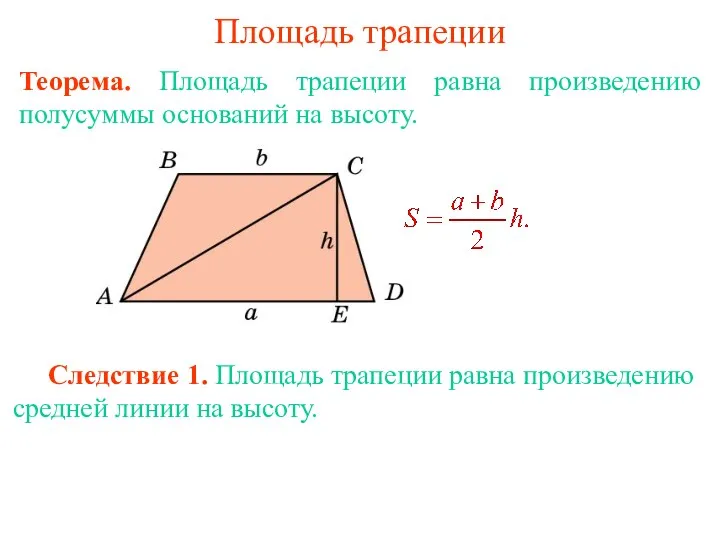 площадь трапеции
площадь трапеции Золотое сечение - божественная мера красоты
Золотое сечение - божественная мера красоты Углы. 7 класс
Углы. 7 класс Теорема о средней линии треугольника
Теорема о средней линии треугольника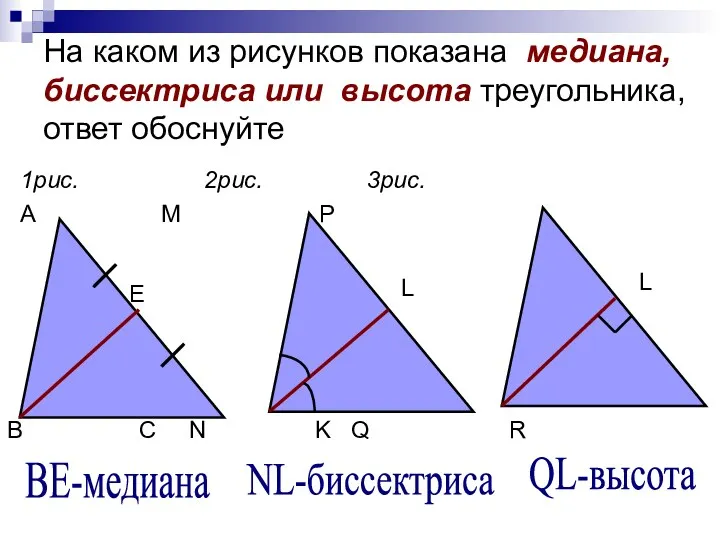 Презентация к уроку по теме: Свойства равнобедренного треугольника
Презентация к уроку по теме: Свойства равнобедренного треугольника Свойства функции
Свойства функции Презентация к уроку геометрии 8класс
Презентация к уроку геометрии 8класс Презентация Центрально-симметричные фигуры
Презентация Центрально-симметричные фигуры Презентация к уроку Теорема Пифагора
Презентация к уроку Теорема Пифагора 7класс Геометрия Перпендикулярные прямые
7класс Геометрия Перпендикулярные прямые Презентация по теме:Понятие движения
Презентация по теме:Понятие движения 7класс Геометрия Сравнение отрезков и углов
7класс Геометрия Сравнение отрезков и углов Математический диктант №2.Первый признак равенства треугольников.Геометрия 7 класс
Математический диктант №2.Первый признак равенства треугольников.Геометрия 7 класс Объём шара. Площадь сферы.
Объём шара. Площадь сферы.