Введение системы координат
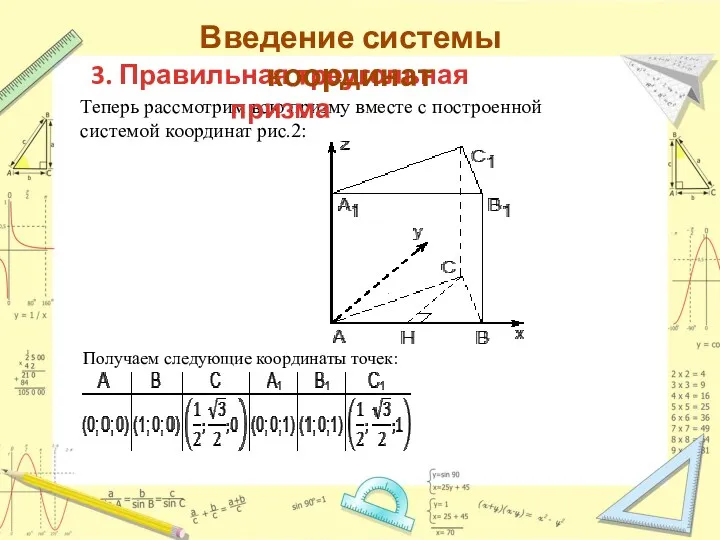
3. Правильная треугольная призма
Вводим систему координат:
Начало координат — в точке A;
Сторону призмы
принимаем за единичный отрезок, если иное не указано в условии задачи;
Ось x направляем по ребру AB, z — по ребру AA1, а ось y расположим так, чтобы плоскость OXY совпадала с плоскостью основания ABC.
ГЛАВНОЕ учесть, что ось y НЕ совпадает с ребром AC, т.к. треугольник ABC — равносторонний, в нем все углы по 60°. А углы между осями координат должны быть по 90°, поэтому вид сверху будет выглядеть так: рис.1.
Проведем в этом треугольнике высоту CH. Треугольник ACH — прямоугольный, причем AC = 1, поэтому
AH = 1 · cos A = cos 60°;
CH = 1 · sin A = sin 60°.
Это надо для вычисления координат точки С.








 Четырёхугольники
Четырёхугольники проект
проект к урокам № 19-20 по геометрии 7 кл
к урокам № 19-20 по геометрии 7 кл Презентация Правиьный многоугольник
Презентация Правиьный многоугольник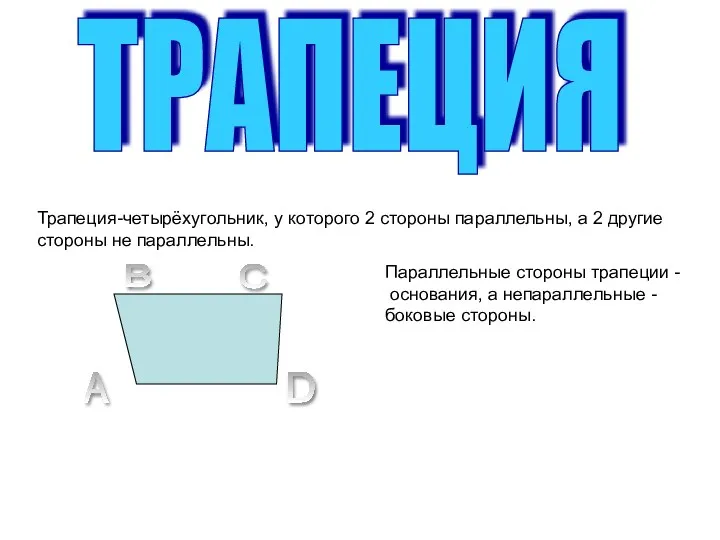 Урок-презентация по геометрии 8 класс на тему Трапеция
Урок-презентация по геометрии 8 класс на тему Трапеция Урок математики в 6 классе по теме Окружность
Урок математики в 6 классе по теме Окружность Смежные углы
Смежные углы Презентация к уроку Подобные треугольники
Презентация к уроку Подобные треугольники Прямоугольные треугольники
Прямоугольные треугольники Урок-практикум Объём цилиндра в заданиях ЕГЭ
Урок-практикум Объём цилиндра в заданиях ЕГЭ Соотношение между сторонами и углами треугольника.
Соотношение между сторонами и углами треугольника. Урок в 7 классе Сумма углов треугольника
Урок в 7 классе Сумма углов треугольника Презентация к уроку по теме: Пирамида
Презентация к уроку по теме: Пирамида Презентация Построение сечений тетраэдра и параллелепипеда
Презентация Построение сечений тетраэдра и параллелепипеда урок-презентация по теме Цилиндр
урок-презентация по теме Цилиндр теорема синусов и косинусов
теорема синусов и косинусов презентация на тему: Теорема Пифагора
презентация на тему: Теорема Пифагора Урок геометрии в 8 классе Свойства площади
Урок геометрии в 8 классе Свойства площади Презентация по теме Симметрия
Презентация по теме Симметрия Презентация урока Правильные фигуры в геометрии
Презентация урока Правильные фигуры в геометрии Открытый урок по геометрии в 8 классе
Открытый урок по геометрии в 8 классе Пирамида
Пирамида Решение геометрических задач при подготовке к ГИА
Решение геометрических задач при подготовке к ГИА Уравнение окружности
Уравнение окружности Свойства прямоугольного треугольника, геометрия 7 класс
Свойства прямоугольного треугольника, геометрия 7 класс Параллельность прямых и плоскостей. Параллельные прямые в пространстве
Параллельность прямых и плоскостей. Параллельные прямые в пространстве Проще простого. Презентация программы предпрофильного курса по математике по теме Геометрические преобразования
Проще простого. Презентация программы предпрофильного курса по математике по теме Геометрические преобразования Прямая и отрезок. Луч и угол
Прямая и отрезок. Луч и угол