Содержание
- 2. Алгоритмизация и программирование. Язык Python § 35. Целочисленные алгоритмы
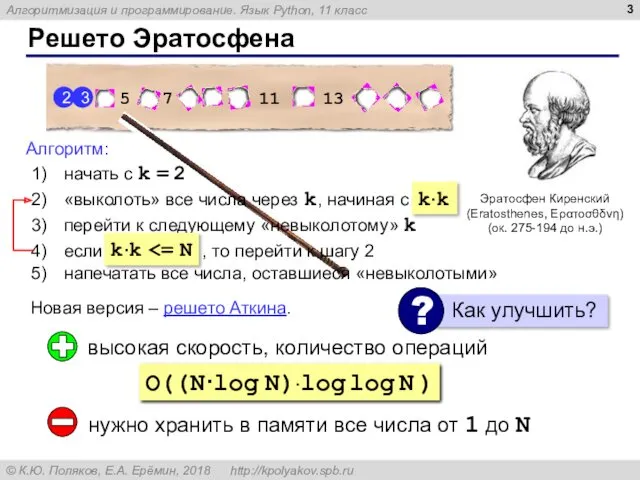
- 3. Решето Эратосфена Эратосфен Киренский (Eratosthenes, Ερατοσθδνη) (ок. 275-194 до н.э.) Новая версия – решето Аткина. 2
- 4. Решето Эратосфена Задача. Вывести все простые числа от 2 до N. Массив (сначала все не вычеркнуты):
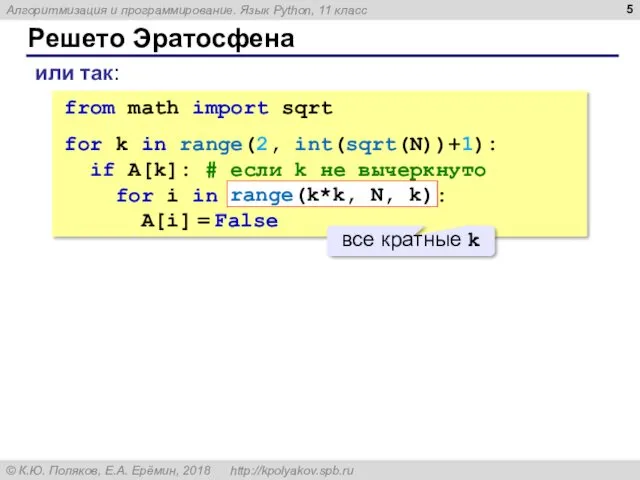
- 5. Решето Эратосфена или так: from math import sqrt for k in range(2, int(sqrt(N))+1): if A[k]: #
- 6. Решето Эратосфена Вывод результата: for i in range(2,N+1): if A[i]: print ( i ) или так:
- 7. «Длинные» числа Ключи для шифрования: ≥ 256 битов. Целочисленные типы данных обычно ≤ 64 битов. Длинное
- 8. «Длинные» числа A = 12345678 неудобно вычислять (с младшего разряда!) неэкономное расходование памяти (одна цифра в
- 9. «Длинные» числа Упаковка элементов: 12345678 = 12·10002 + 345·10001 + 678·10000 система счисления с основанием 1000!
- 10. Вычисление факториала Задача 1. Вычислить точно значение факториала 100! = 1·2·3·…·99·100 1·2·3·…·99·100 201 цифра 6 цифр
- 11. Вычисление факториала основание d = 1 000 000 [A] = 12345678901734567 734 567·3 = 2 203
- 12. Вычисление факториала r = 0 for i in range(len(A)): s = A[i]*k + r A[i] =
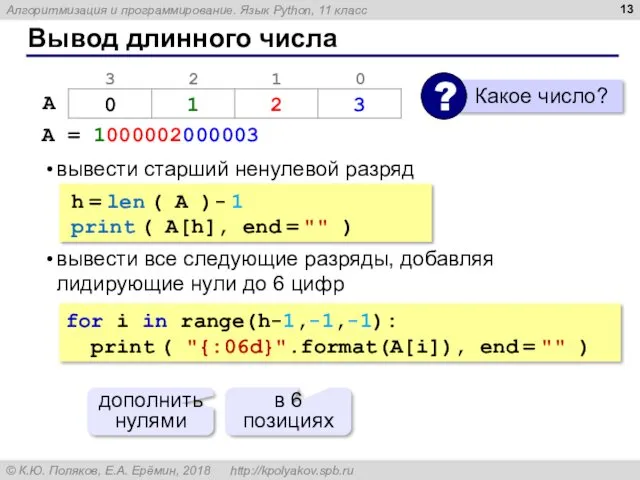
- 13. Вывод длинного числа A = 1000002000003 вывести старший ненулевой разряд вывести все следующие разряды, добавляя лидирующие
- 14. Квадратный корень Задача. Извлечь квадратный корень из «длинного» целого числа; если это не целое число, найти
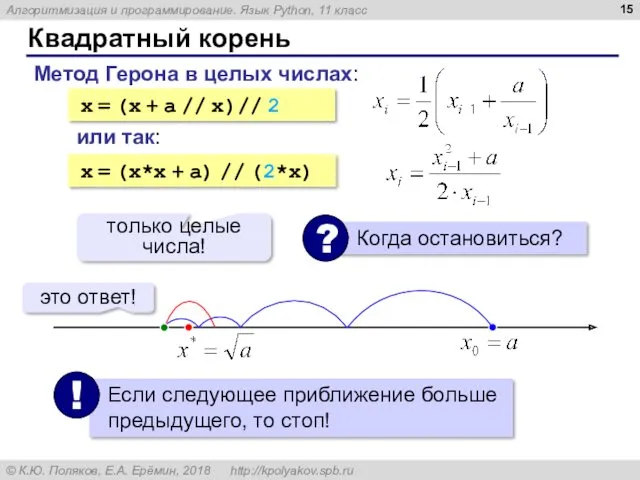
- 15. Квадратный корень Метод Герона в целых числах: x = (x + a // x)// 2 x
- 16. Квадратный корень Метод Герона в целых числах: def isqrt(a): x = a # начальное приближение while
- 17. Алгоритмизация и программирование. Язык Python § 36. Структуры
- 18. Зачем нужны структуры? Книги в библиотеках: автор название количество экземпляров … символьные строки целое число Задачa:
- 19. Структуры Структура – это тип данных, который может включать в себя несколько полей – элементов разных
- 20. Работа со структурами B = TBook() Заполнение: B.author = "Пушкин А.С." B.title = "Полтава" B.count =
- 21. Работа со структурами Обработка: B.author = "Пушкин А.С." fam = B.author.split()[0] # фамилия print ( fam
- 22. Массив структур Books = [TBook()]*100 Создание: Books[5].author = "Пушкин А.С." Books[5].title = "Полтава" Books[5].count = 1
- 23. Запись структур в файлы "Пушкин А.С.";"Полтава";12 "Лермонтов М.Ю.";"Мцыри";8 Текстовые файлы: разделитель Двоичные файлы: B = TBook()
- 24. Запись массива структур в файлы pickle.dump ( Books, F ); Сразу все: По одной структуре: for
- 25. Чтение структур из файла F = open ( "books.dat", "rb" ) B = pickle.load ( F
- 26. Чтение структур из файла Books = [] while True: try: B = pickle.load ( F )
- 27. Сортировка структур Ключ – фамилия автора: # B – массив структур TBook N = len(B) for
- 28. Сортировка структур (в стиле Python) def getAuthor ( B ): return B.author Books.sort ( key =
- 29. Алгоритмизация и программирование. Язык Python § 37. Словари
- 30. Что такое словарь? Задача. В файле находится список слов, среди которых есть повторяющиеся. Каждое слово записано
- 31. Алгоритм (псевдокод) создать пустой словарь while есть слова в файле: прочитать очередное слово if слово есть
- 32. Работа со словарями в Python D = {} # пустой словарь Создание: D = { "бегемот":
- 33. Работа со словарями в Python Изменение с проверкой: if "самолёт" in D: D["самолёт"] += 1 else:
- 34. Основной цикл D = {} F = open ( "input.txt" ) while True: word = F.readline().strip()
- 35. Вывод результата allKeys = D.keys() Получить массив всех ключей: sortKeys = sorted(D.keys()) отсортировать ключи: или так:
- 36. Ещё о словарях for i in D.values(): print ( i ) Перебор значений: for k, v
- 37. Словарь и массив пар Массив (список) пар «ключ-значение»: A = list(D.items()) D = {"бам": 2, "там":
- 38. Словарь и массив пар Сортировка: A.sort() по ключам, если ключи равны – по значениям A.sort( key
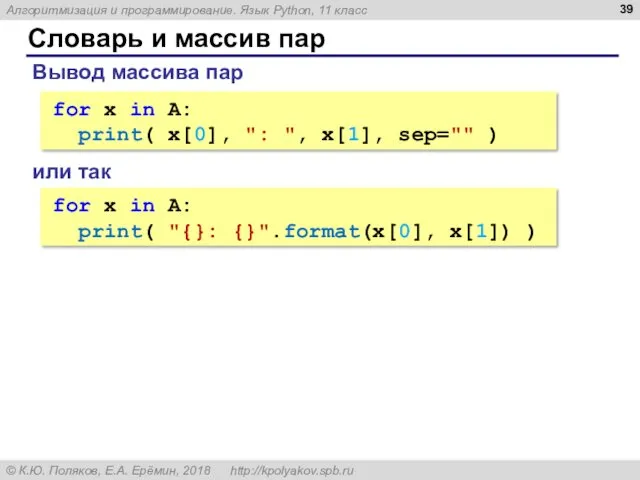
- 39. Словарь и массив пар Вывод массива пар for x in A: print( x[0], ": ", x[1],
- 40. Алгоритмизация и программирование. Язык Python § 38. Стек, дек, очередь
- 41. Что такое стек? Стек (англ. stack – стопка) – это линейный список, в котором элементы добавляются
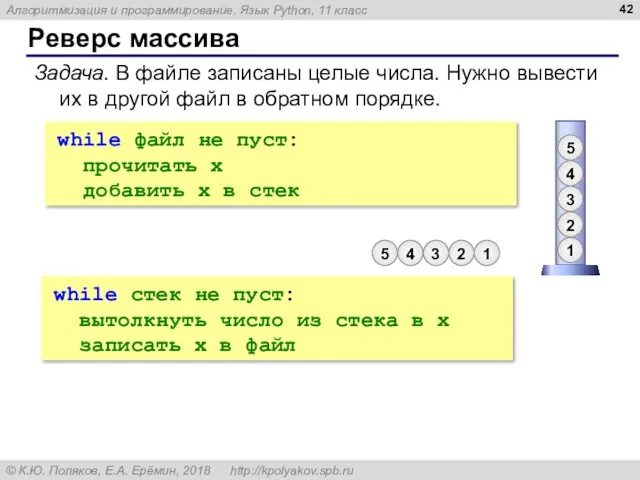
- 42. Реверс массива Задача. В файле записаны целые числа. Нужно вывести их в другой файл в обратном
- 43. Использование списка stack = [] Создать стек: stack.append ( x ) «Втолкнуть» x в стек: x
- 44. Инверсия массива неизвестной длины F = open ( "input.txt" ) stack = [] while True: s
- 45. Инверсия массива неизвестной длины F = open ( "output.txt", "w" ) while len(stack) > 0: x
- 46. Вычисление арифметических выражений (5+15)/(4+7-1) инфиксная форма (знак операции между данными) первой стоит последняя операция (вычисляем с
- 47. Вычисление арифметических выражений (5+15)/(4+7-1) 1950-е: постфиксная форма (знак операции после данных) не нужны скобки вычисляем с
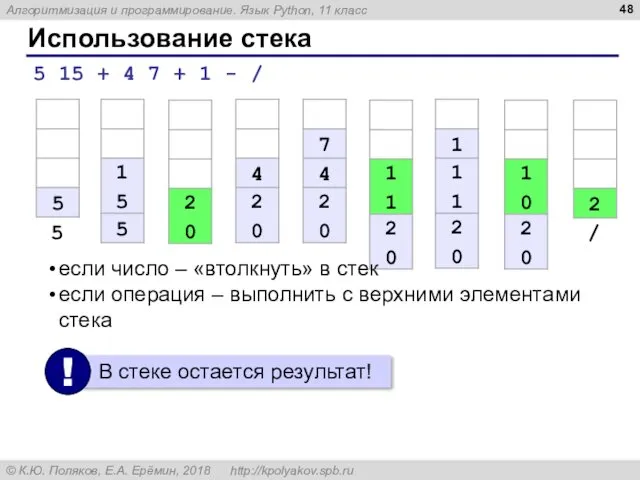
- 48. Использование стека 5 15 + 4 7 + 1 - / 5 15 + 4 7
- 49. Вычисление постфиксной формы data = input().split() stack = [] for x in data: if x in
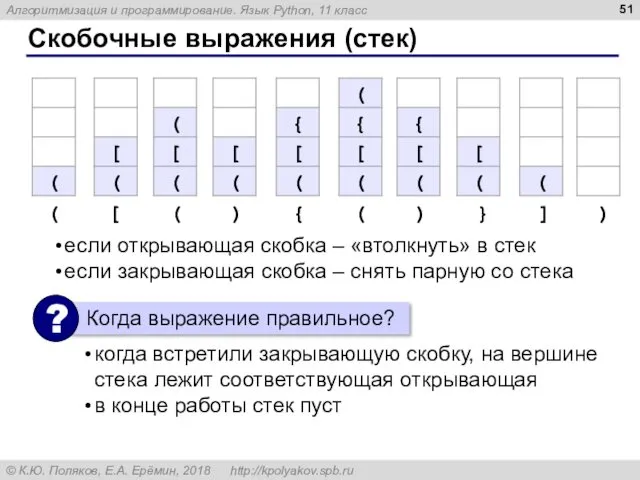
- 50. Скобочные выражения Задача. Вводится символьная строка, в которой записано некоторое (арифметическое) выражение, использующее скобки трёх типов:
- 51. Скобочные выражения (стек) когда встретили закрывающую скобку, на вершине стека лежит соответствующая открывающая в конце работы
- 52. Скобочные выражения (стек) pairs = {"(": ")", "[": "]", "{": "}"} stack = [] # пустой
- 53. Скобочные выражения (стек) for c in s: if c in pairs: stack.append( pairs[c] ) elif c
- 54. Что такое очередь? Очередь – это линейный список, для которого введены две операции: • добавление элемента
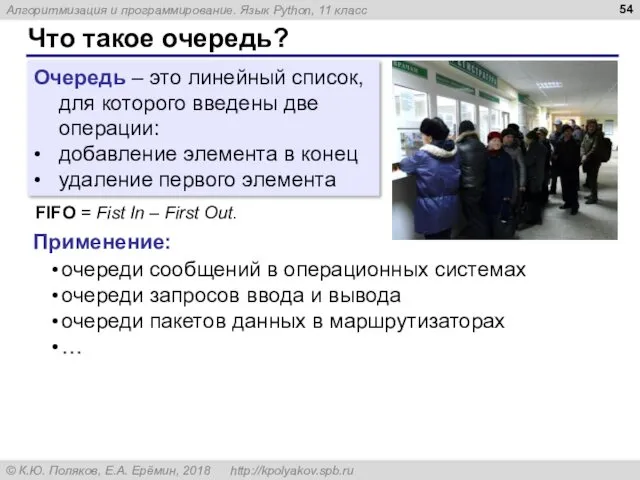
- 55. Заливка области Задача. Рисунок задан в виде матрицы A, в которой элемент A[y][x] определяет цвет пикселя
- 56. Заливка: использование очереди добавить в очередь точку (x0,y0) color = цвет начальной точки while очередь не
- 57. Заливка YMAX = len(A) XMAX = len(A[0]) NEW_COLOR = 2 y0 = 0 x0 = 1
- 58. Заливка (основной цикл) while len(Q) > 0: x, y = Q.pop(0) if A[y][x] == color: A[y][x]
- 59. Очередь: статический массив нужно знать размер не двигаем элементы голова хвост Удаление элемента: Добавление элемента:
- 60. Очередь: статический массив Замыкание в кольцо: Очередь заполнена: Очередь пуста:
- 61. Что такое дек? Дек – это линейный список, в котором можно добавлять и удалять элементы как
- 62. Алгоритмизация и программирование. Язык Python § 39. Деревья
- 63. Что такое дерево? «Сыновья» А: B, C. «Родитель» B: A. «Потомки» А: B, C, D, E,
- 64. Рекурсивные определения пустая структура – это дерево дерево – это корень и несколько связанных с ним
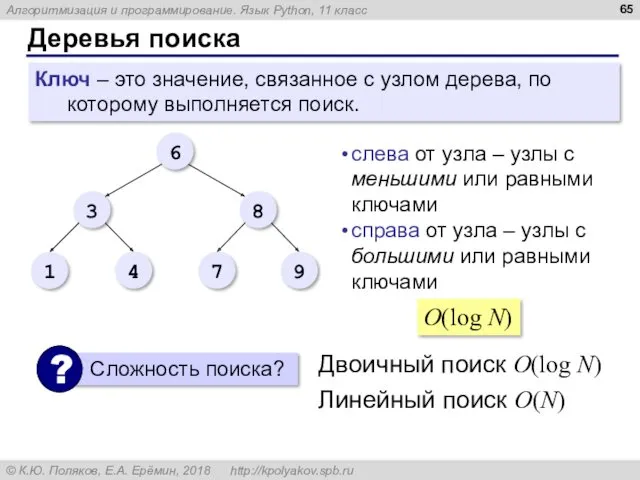
- 65. Деревья поиска Ключ – это значение, связанное с узлом дерева, по которому выполняется поиск. слева от
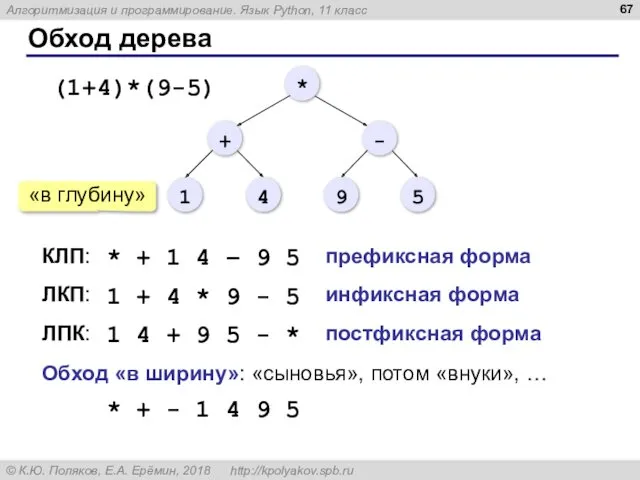
- 66. Обход дерева Обойти дерево ⇔ «посетить» все узлы по одному разу. ⇒ список узлов КЛП –
- 67. Обход дерева ЛПК: КЛП: ЛКП: * + 1 4 – 9 5 1 + 4 *
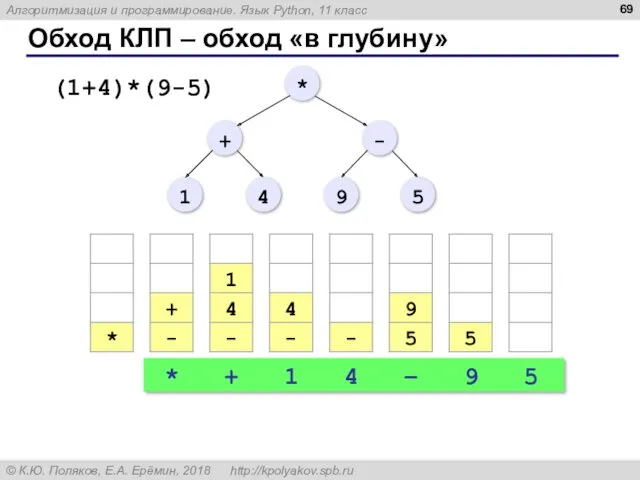
- 68. Обход КЛП – обход «в глубину» записать в стек корень дерева while стек не пуст: выбрать
- 69. Обход КЛП – обход «в глубину» * + 1 4 – 9 5
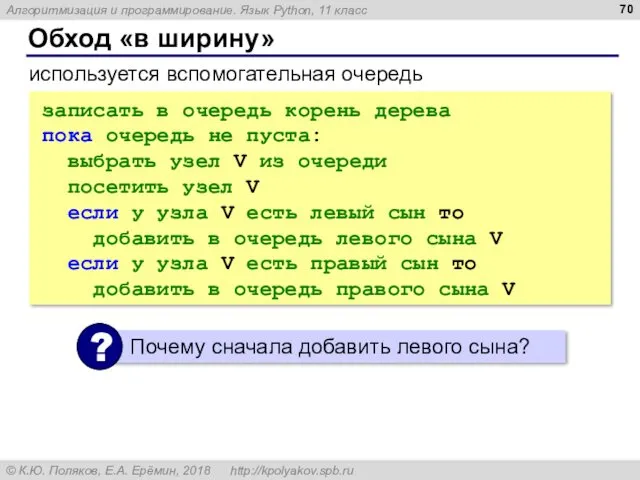
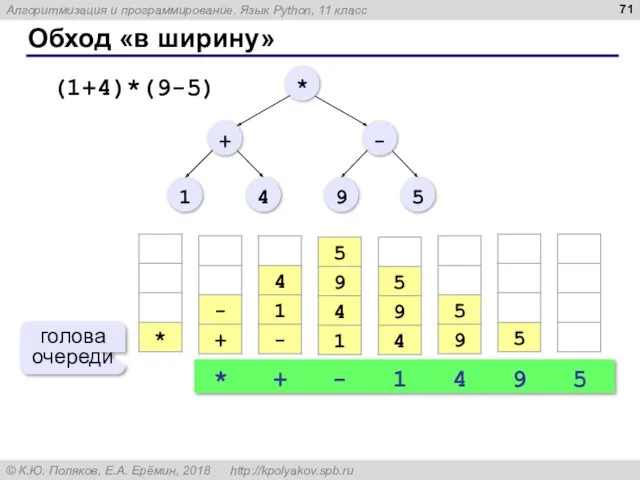
- 70. Обход «в ширину» записать в очередь корень дерева пока очередь не пуста: выбрать узел V из
- 71. Обход «в ширину» (1+4)*(9-5) * + - 1 4 9 5 голова очереди
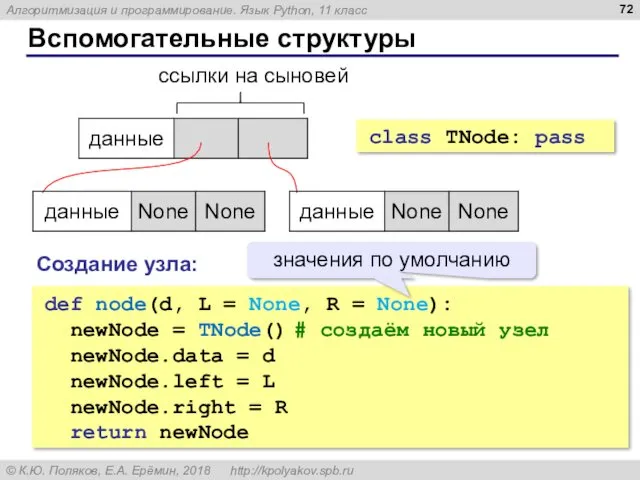
- 72. Вспомогательные структуры ссылки на сыновей class TNode: pass def node(d, L = None, R = None):
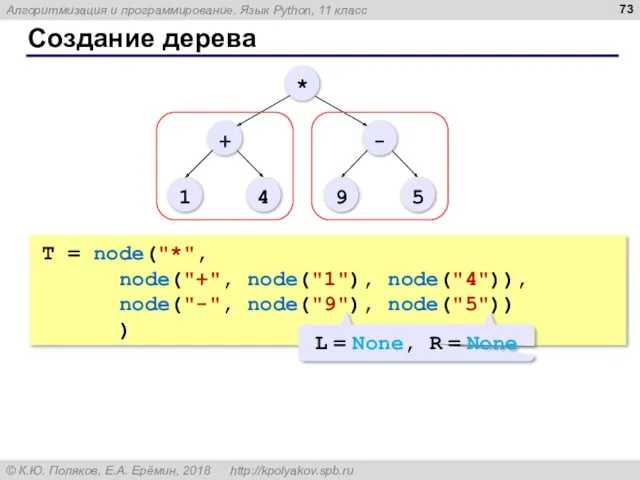
- 73. Создание дерева T = node("*", node("+", node("1"), node("4")), node("-", node("9"), node("5")) )
- 74. Обход дерева в глубину def DFS( T ): if not T: return print(T.data, end=" ") DFS(T.left)
- 75. Обход дерева в ширину def BFS ( T ): queue = [T] while queue: V =
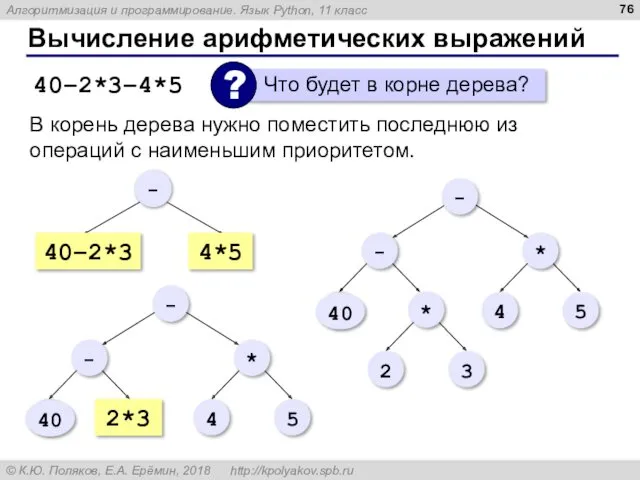
- 76. Вычисление арифметических выражений 40–2*3–4*5 В корень дерева нужно поместить последнюю из операций с наименьшим приоритетом.
- 77. Вычисление арифметических выражений найти последнюю выполняемую операцию if операций нет: создать узел-лист return поместить операцию в
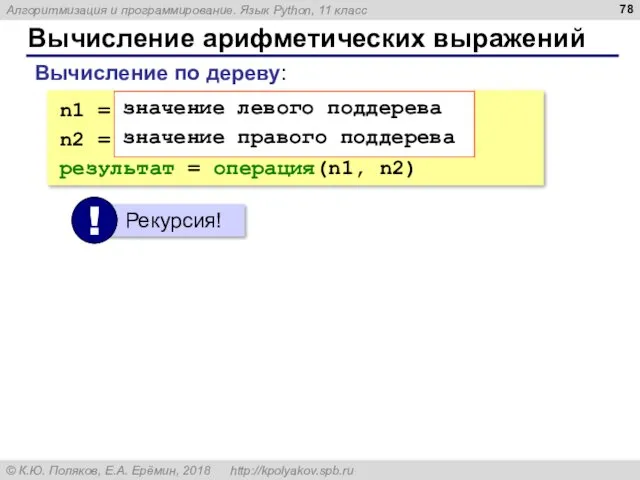
- 78. Вычисление арифметических выражений n1 = значение левого поддерева n2 = значение правого поддерева результат = операция(n1,
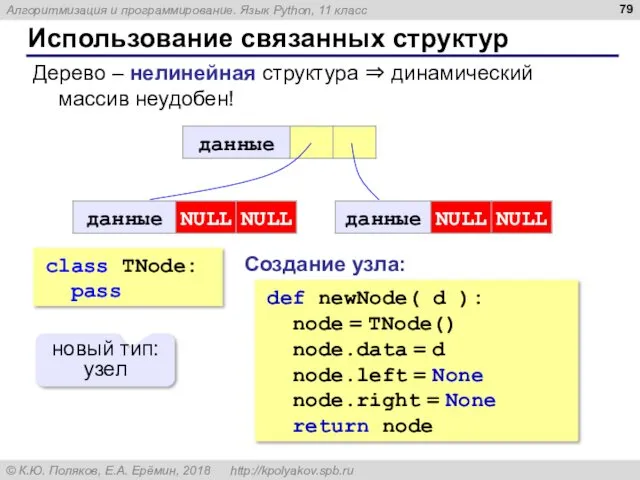
- 79. Использование связанных структур Дерево – нелинейная структура ⇒ динамический массив неудобен! class TNode: pass новый тип:
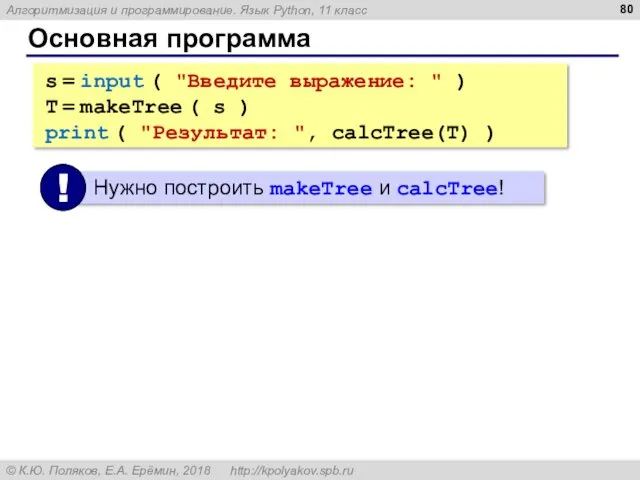
- 80. Основная программа s = input ( "Введите выражение: " ) T = makeTree ( s )
- 81. Построение дерева def makeTree ( s ): k = lastOp(s) # номер последней операции if k
- 82. Вычисление по дереву def calcTree ( Tree ): if Tree.left == None: return int(Tree.data) else: n1
- 83. Вспомогательные функции def priority ( op ): if op in "+-": return 1 if op in
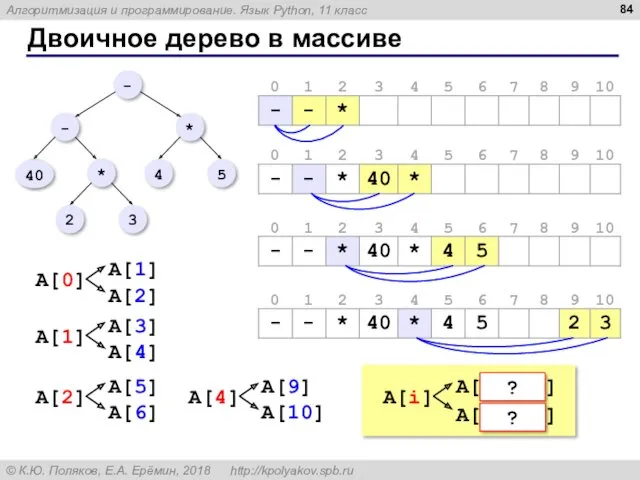
- 84. Двоичное дерево в массиве ? ?
- 85. Алгоритмизация и программирование. Язык Python § 40. Графы
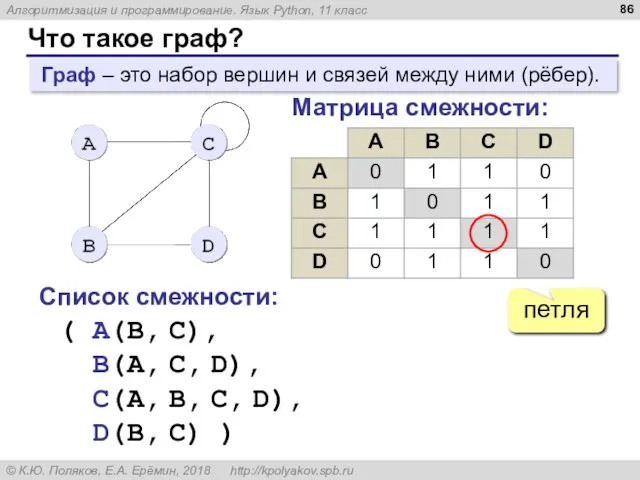
- 86. Что такое граф? Граф – это набор вершин и связей между ними (рёбер). петля Матрица смежности:
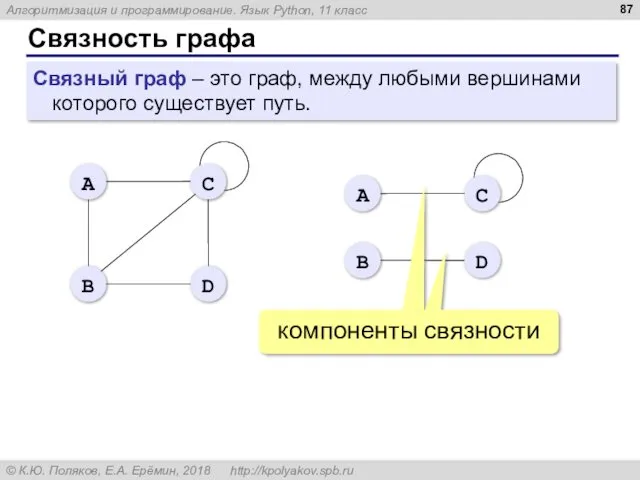
- 87. Связность графа Связный граф – это граф, между любыми вершинами которого существует путь.
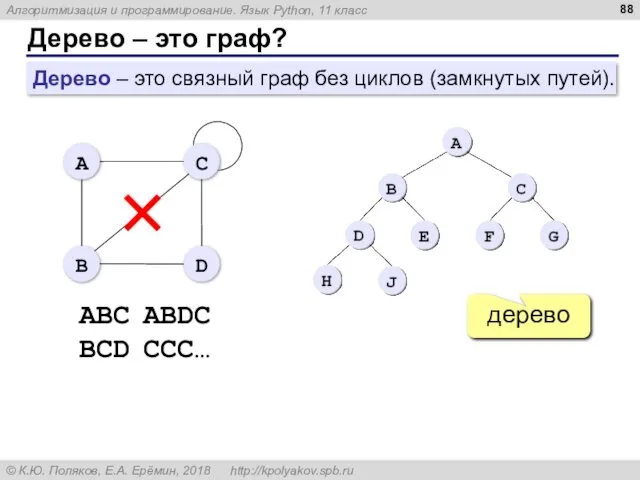
- 88. Дерево – это граф? дерево ABC ABDC BCD CCC… Дерево – это связный граф без циклов
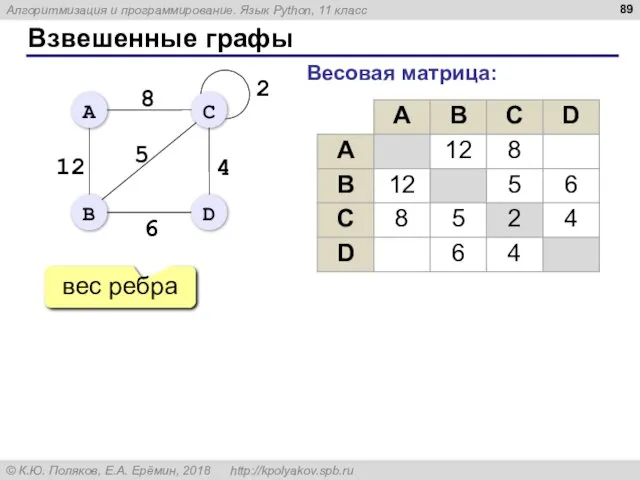
- 89. Взвешенные графы Весовая матрица: вес ребра
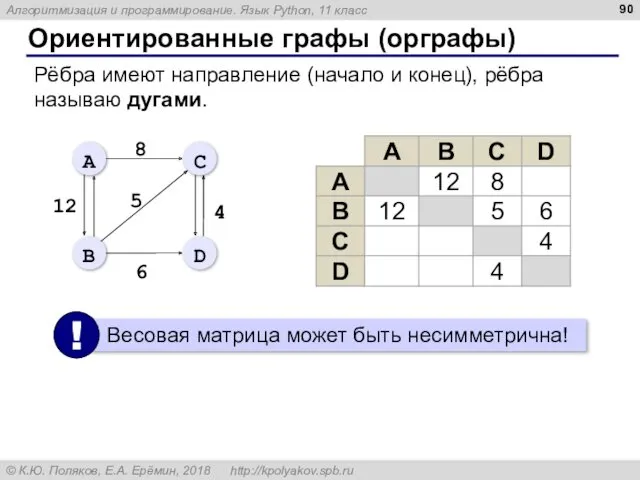
- 90. Ориентированные графы (орграфы) Рёбра имеют направление (начало и конец), рёбра называю дугами.
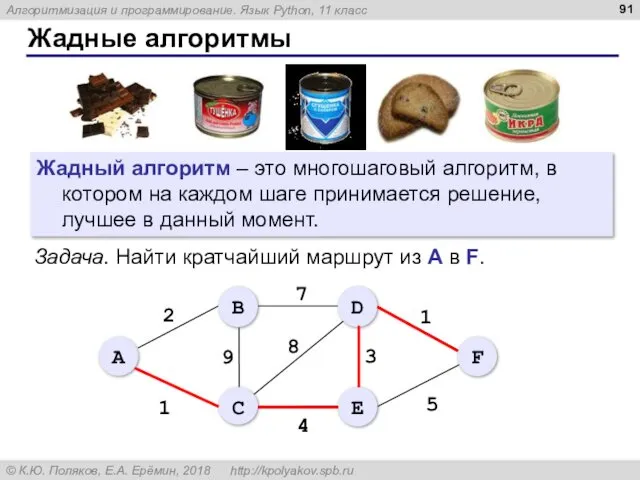
- 91. Жадные алгоритмы Жадный алгоритм – это многошаговый алгоритм, в котором на каждом шаге принимается решение, лучшее
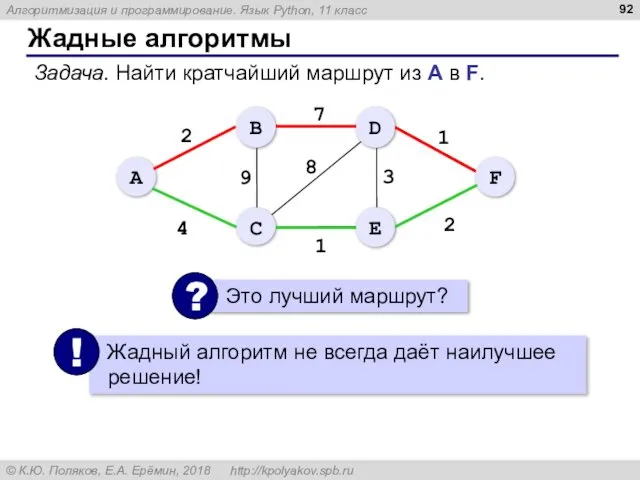
- 92. Жадные алгоритмы Задача. Найти кратчайший маршрут из А в F.
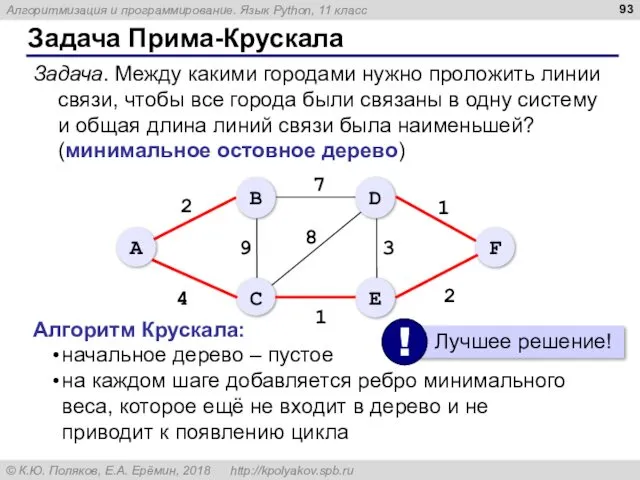
- 93. Задача Прима-Крускала Задача. Между какими городами нужно проложить линии связи, чтобы все города были связаны в
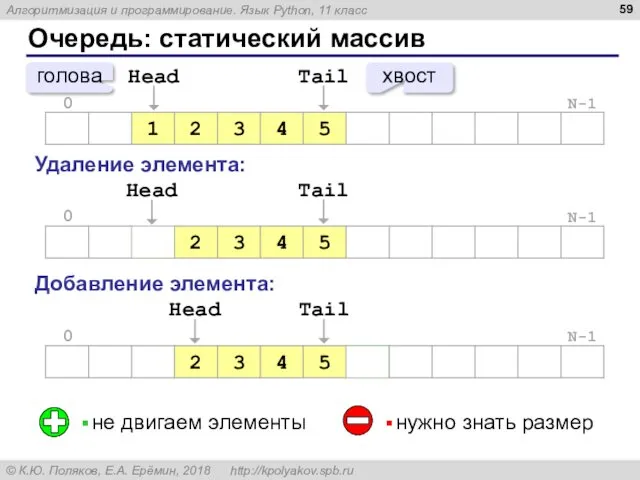
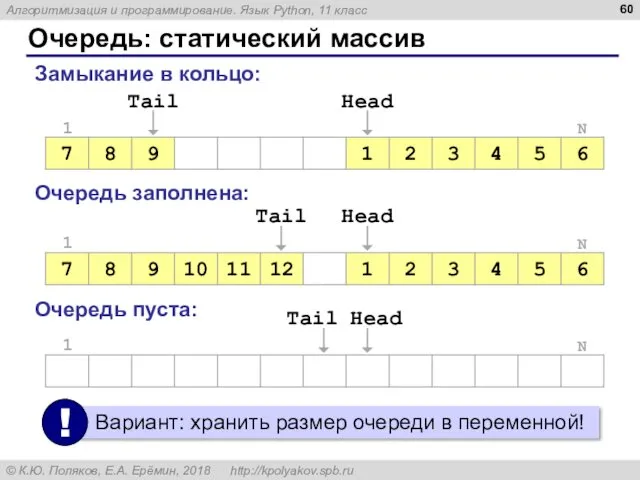
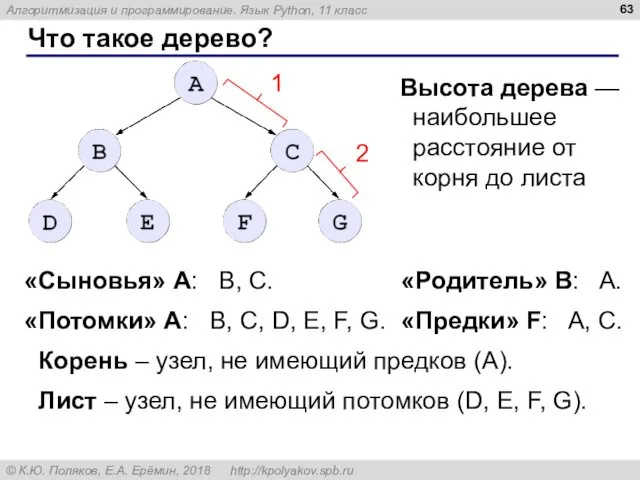
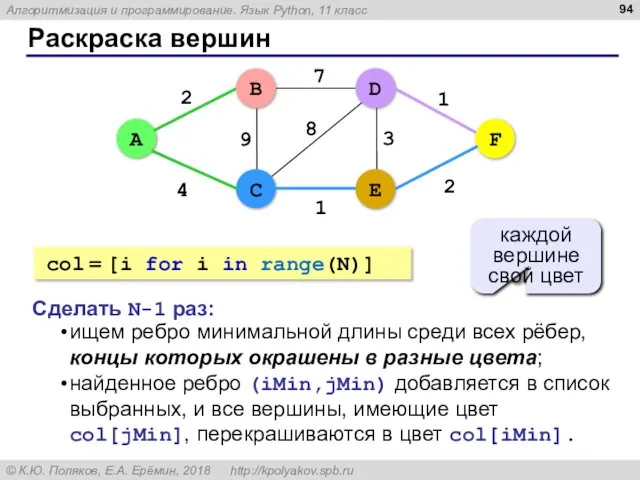
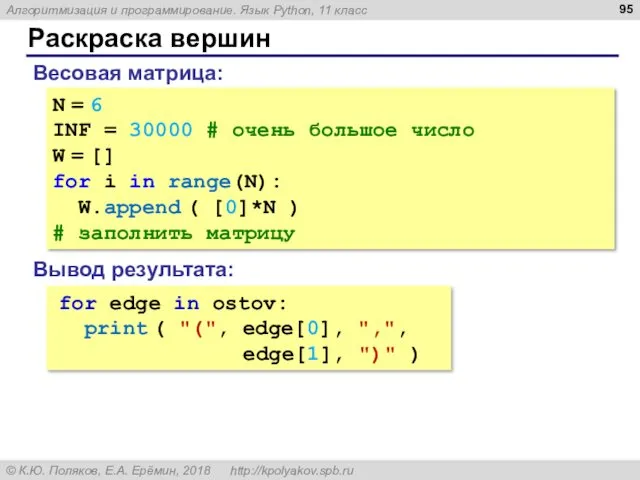
- 94. Раскраска вершин 4 B 2 1 2 9 7 8 1 3 D E F A
- 95. Раскраска вершин N = 6 INF = 30000 # очень большое число W = [] for
- 96. Раскраска вершин ostov = [] # список выбранных рёбер for k in range(N-1): minDist = INF
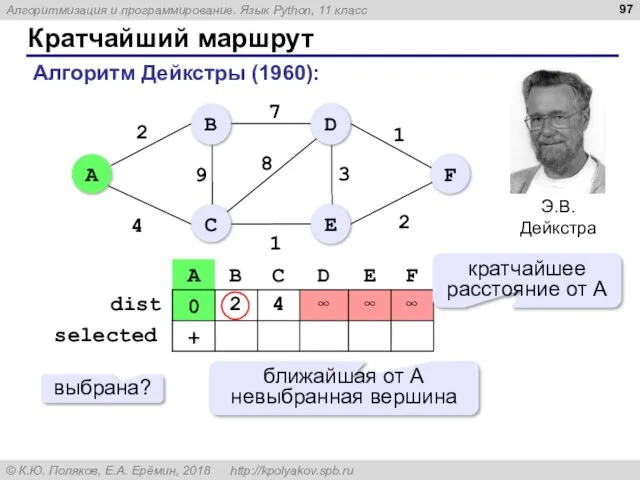
- 97. Кратчайший маршрут Алгоритм Дейкстры (1960): ближайшая от A невыбранная вершина кратчайшее расстояние от A выбрана?
- 98. Кратчайший маршрут Алгоритм Дейкстры (1960): W[x,z] + W[z,y] может быть так, что 9
- 99. Кратчайший маршрут Алгоритм Дейкстры (1960): W[x,z] + W[z,y] может быть так, что 5
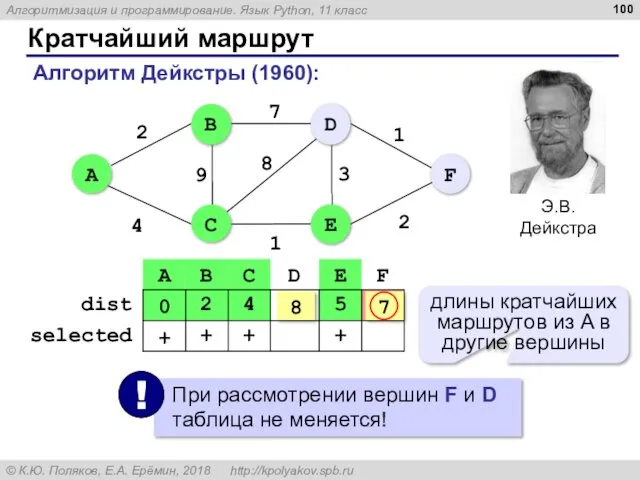
- 100. Кратчайший маршрут Алгоритм Дейкстры (1960): 7 8 длины кратчайших маршрутов из A в другие вершины
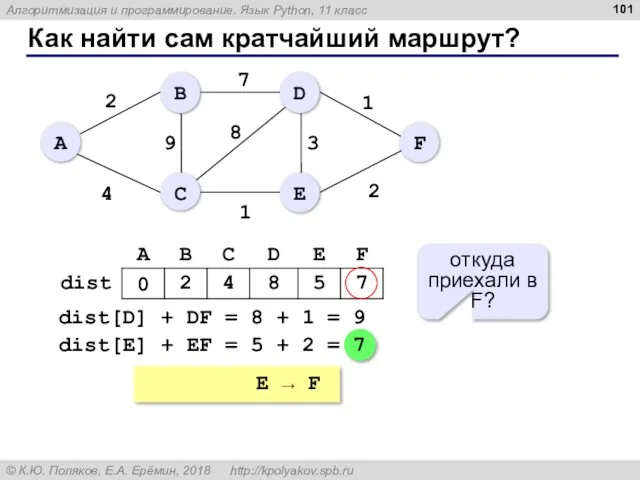
- 101. Как найти сам кратчайший маршрут? A → C → E → F dist[D] + DF =
- 102. Алгоритм Дейкстры N = 6 W = [] for i in range(N): W.append ( [0]*N )
- 103. Алгоритм Дейкстры minDist = 0 while minDist selected[V] = True # проверка маршрутов через вершину V
- 104. Алгоритм Дейкстры V = N - 1 print(V) while V != start: for i in range(N):
- 105. Алгоритм Флойда for k in range(N): for i in range(N): for j in range(N): if W[i][k]
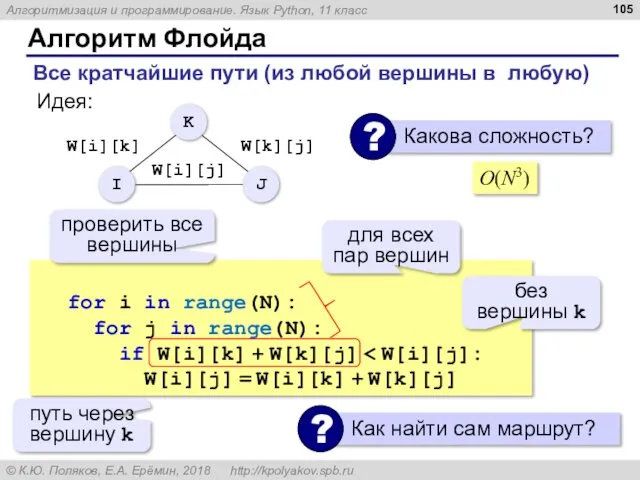
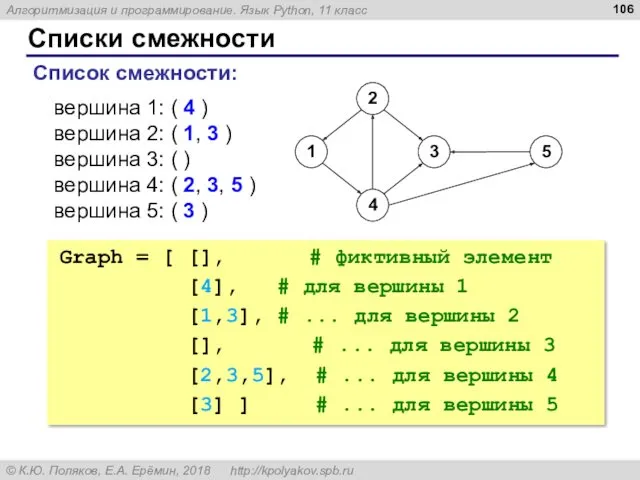
- 106. Списки смежности вершина 1: ( 4 ) вершина 2: ( 1, 3 ) вершина 3: (
- 107. Списки смежности Graph = [[], [4], [1,3], [], [2,3,5], [3]] print ( pathCount (Graph, 1, 3,
- 108. Число путей: функция def pathCount ( graph, vStart, vEnd, visited ): if vStart == vEnd: return
- 109. Задача коммивояжера Коммивояжер (бродячий торговец) должен выйти из города 1 и, посетив по разу в неизвестном
- 110. Некоторые задачи Задача на минимум суммы. Имеется N домов, в каждом из которых живет pi жителей
- 111. Алгоритмизация и программирование. Язык Python § 41. Динамическое программирование
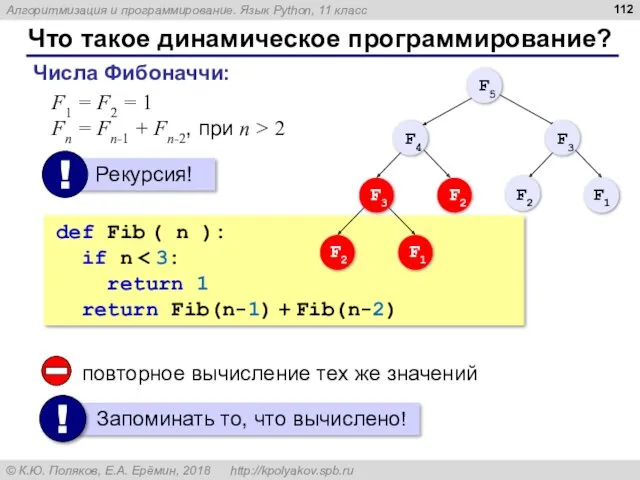
- 112. Что такое динамическое программирование? Числа Фибоначчи: ; . F1 = F2 = 1 Fn = Fn-1
- 113. Динамическое программирование Создание массива: F = [1]*(N+1) # чтобы начать с 1 Заполнение массива: for i
- 114. Динамическое программирование Динамическое программирование – это способ решения сложных задач путем сведения их к более простым
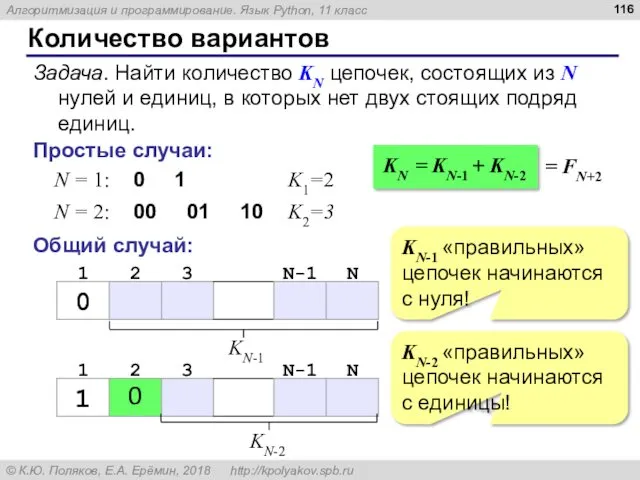
- 115. Количество вариантов Задача. Найти количество KN цепочек, состоящих из N нулей и единиц, в которых нет
- 116. Количество вариантов Задача. Найти количество KN цепочек, состоящих из N нулей и единиц, в которых нет
- 117. Оптимальное решение Задача. В цистерне N литров молока. Есть бидоны объемом 1, 5 и 6 литров.
- 118. Оптимальное решение Сначала выбрали бидон… KN – минимальное число бидонов для N литров KN = 1
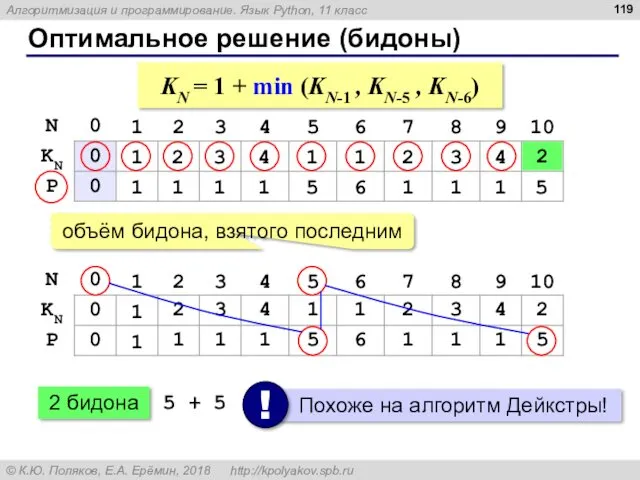
- 119. Оптимальное решение (бидоны) 1 1 2 1 3 1 4 1 1 5 1 6 2
- 120. Задача о куче Задача. Из камней весом pi (i=1, …, N) набрать кучу весом ровно W
- 121. Задача о куче Задача. Из камней весом pi (i=1, …, N) набрать кучу весом ровно W
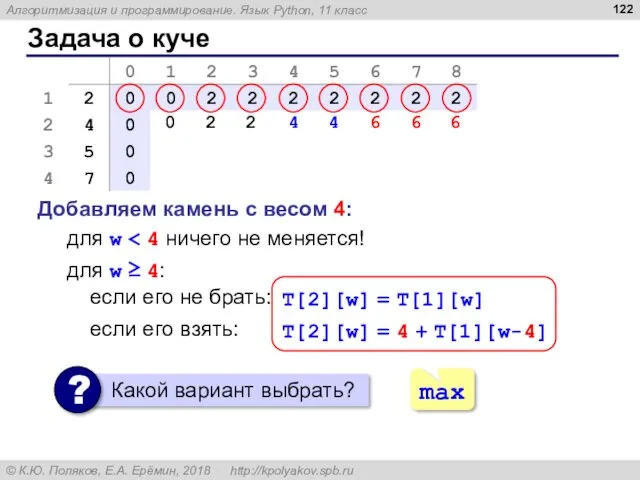
- 122. Задача о куче Добавляем камень с весом 4: для w 0 2 2 для w ≥
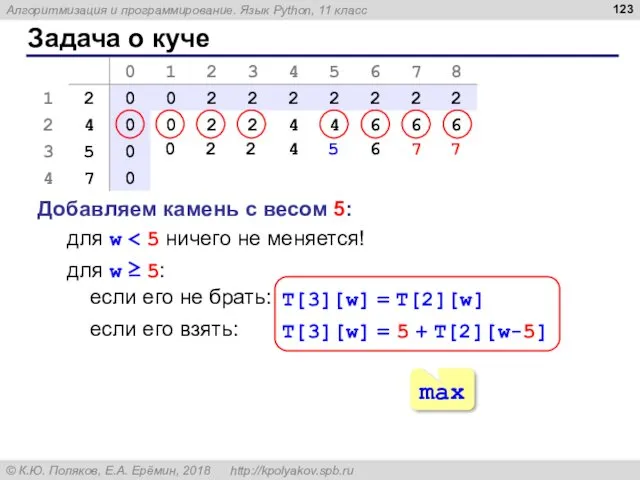
- 123. Задача о куче Добавляем камень с весом 5: для w 0 2 2 4 5 6
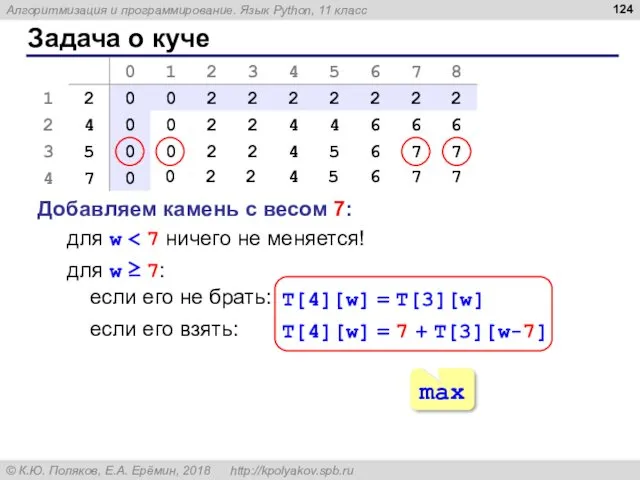
- 124. Задача о куче Добавляем камень с весом 7: для w 0 2 2 4 5 6
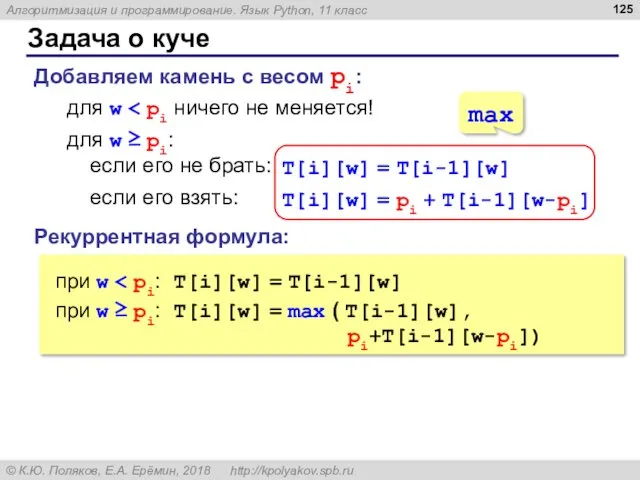
- 125. Задача о куче Добавляем камень с весом pi: для w Рекуррентная формула:
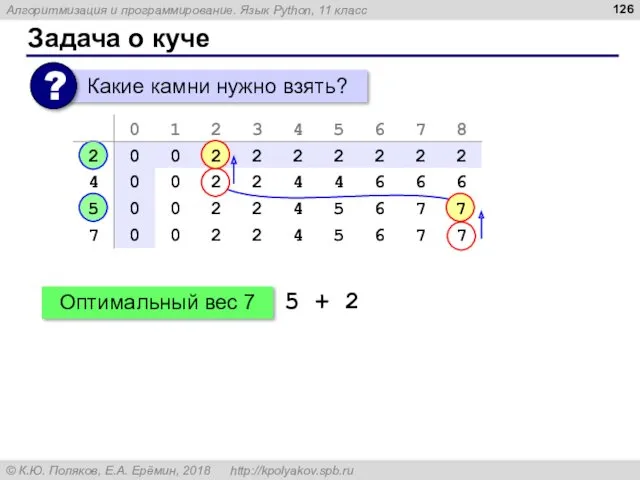
- 126. Задача о куче Оптимальный вес 7 5 + 2
- 127. Задача о куче Заполнение таблицы: W+1 N псевдополиномиальный
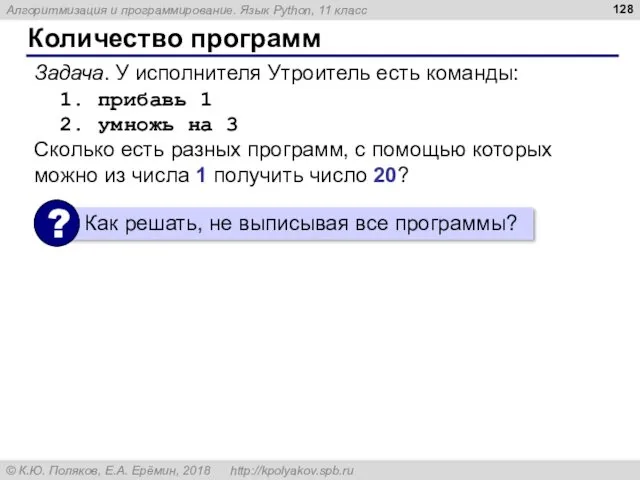
- 128. Количество программ Задача. У исполнителя Утроитель есть команды: 1. прибавь 1 2. умножь на 3 Сколько
- 129. Количество программ Как получить число N: N если делится на 3! последняя команда Рекуррентная формула: KN
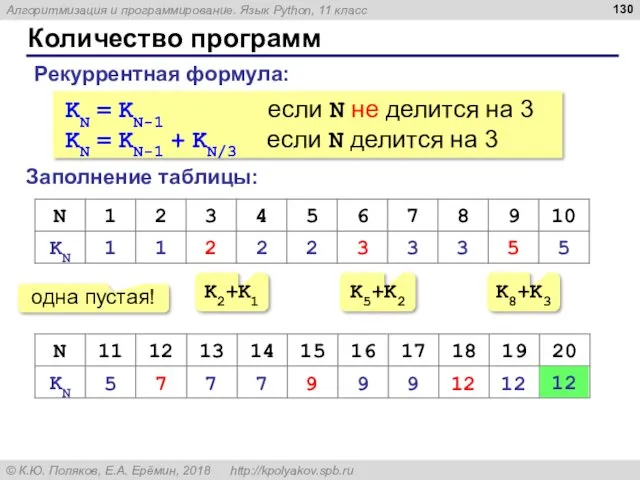
- 130. Количество программ Заполнение таблицы: Рекуррентная формула: KN = KN-1 если N не делится на 3 KN
- 131. Количество программ Только точки изменения: 12 20 Программа: K = [0]*(N+1) K[1] = 1 for i
- 132. Размен монет Задача. Сколькими различными способами можно выдать сдачу размером W рублей, если есть монеты достоинством
- 133. Размен монет Пример: W = 10, монеты 1, 2, 5 и 10 w pi базовые случаи
- 134. Размен монет Пример: W = 10, монеты 1, 2, 5 и 10 Рекуррентная формула (добавили монету
- 135. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург kpolyakov@mail.ru ЕРЕМИН
- 137. Скачать презентацию


![Решето Эратосфена Вывод результата: for i in range(2,N+1): if A[i]:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-5.jpg)




![Вычисление факториала основание d = 1 000 000 [A] =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-10.jpg)








![Массив структур Books = [TBook()]*100 Создание: Books[5].author = "Пушкин А.С."](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-21.jpg)



![Чтение структур из файла Books = [] while True: try:](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-25.jpg)










![Использование списка stack = [] Создать стек: stack.append ( x](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-42.jpg)




![Вычисление постфиксной формы data = input().split() stack = [] for](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-48.jpg)

![Скобочные выражения (стек) pairs = {"(": ")", "[": "]", "{":](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-51.jpg)



![Заливка YMAX = len(A) XMAX = len(A[0]) NEW_COLOR = 2](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-56.jpg)













![Раскраска вершин ostov = [] # список выбранных рёбер for](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-95.jpg)
![Кратчайший маршрут Алгоритм Дейкстры (1960): W[x,z] + W[z,y] может быть так, что 9](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-97.jpg)
![Кратчайший маршрут Алгоритм Дейкстры (1960): W[x,z] + W[z,y] может быть так, что 5](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-98.jpg)
![Алгоритм Дейкстры N = 6 W = [] for i](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-101.jpg)
![Алгоритм Дейкстры minDist = 0 while minDist selected[V] = True](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-102.jpg)

![Списки смежности Graph = [[], [4], [1,3], [], [2,3,5], [3]]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-106.jpg)




![Динамическое программирование Создание массива: F = [1]*(N+1) # чтобы начать](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/17110/slide-112.jpg)













 Algebra relacyjna. Wprowadzenie do systemów baz danych
Algebra relacyjna. Wprowadzenie do systemów baz danych Знакомство с ТРИК Студией
Знакомство с ТРИК Студией Использование информационно-коммуникационных технологий в преподавании физики
Использование информационно-коммуникационных технологий в преподавании физики Метод побудови раціональної архітектури мережі 5G на основі існуючих 4G мереж
Метод побудови раціональної архітектури мережі 5G на основі існуючих 4G мереж Автоматизированные рабочие места автоматизированного управления (тема 9)
Автоматизированные рабочие места автоматизированного управления (тема 9) Технологии 3Dпечати, применяемые на АО НПК Уралвагонзавод
Технологии 3Dпечати, применяемые на АО НПК Уралвагонзавод Анализ публикаций в этно-СМИ Московская немецкая газета. Итоговый исследовательский проект по дисциплине Этножурналистика
Анализ публикаций в этно-СМИ Московская немецкая газета. Итоговый исследовательский проект по дисциплине Этножурналистика Компьютерные презентации. Мультимедиа
Компьютерные презентации. Мультимедиа Пространственные методы улучшения изображений
Пространственные методы улучшения изображений Интегрированный урок Математика - информатика
Интегрированный урок Математика - информатика How to install Java
How to install Java Нейронна мережа Джордана
Нейронна мережа Джордана Разграничение прав доступа в сети. Общее дисковое пространство в локальной сети
Разграничение прав доступа в сети. Общее дисковое пространство в локальной сети Массивы. Лекция 2
Массивы. Лекция 2 Математичні функцій в С++
Математичні функцій в С++ Презентация Безопасный Интернет
Презентация Безопасный Интернет Информационная безопасность и кибербезопасность
Информационная безопасность и кибербезопасность Лекция 2 – Основы языка C#
Лекция 2 – Основы языка C# Медиасистемы. Основы терминологического анализа. Основные типологические характеристики
Медиасистемы. Основы терминологического анализа. Основные типологические характеристики Управление памятью в ОСС
Управление памятью в ОСС Стандарты в области компьютерной графики
Стандарты в области компьютерной графики 1. Обработка символьной информации. Символьные переменные
1. Обработка символьной информации. Символьные переменные презентация Информационные технологии
презентация Информационные технологии Представление (кодирование) чисел
Представление (кодирование) чисел Графический дизайн
Графический дизайн Розробка системи обміну повідомленнями для Twitter, на базі мобільних технологій
Розробка системи обміну повідомленнями для Twitter, на базі мобільних технологій Кодирование графической информации
Кодирование графической информации BIM: Междисциплинарная координация
BIM: Междисциплинарная координация