Содержание
- 2. Зачем уточнять определение? Алгоритм – точный набор инструкций для исполнителя. Конструктивное доказательство: построить алгоритм. задача о
- 3. Зачем уточнять определение? Задача: алгоритм как математический объект. доказательство алгоритмической неразрешимости задач анализ сложности алгоритмов сравнительная
- 4. Что такое алгоритм? Первые алгоритмы – правила арифметических действий: Все объекты можно закодировать как символьные строки:
- 5. Как работает алгоритм? дискретный объект 1 2 3 4 алгоритм шаг 1 шаг 2 шаг 3
- 6. Как работает алгоритм? т.е. правило преобразования входа в выход Функция не определена ⇔ алгоритм зацикливается или
- 7. Эквивалентные алгоритмы Задают одну и ту же функцию: если a M:= a иначе M:= b все
- 8. Универсальные исполнители Алгоритм привязан к исполнителю ⇒ идея: построить универсального исполнителя. Для любого алгоритма для любого
- 9. Универсальные исполнители Алгоритм – это программа для универсального исполнителя. Модель вычислений: «процессор» (система команд и способ
- 10. Универсальные исполнители машина Тьюринга машина Поста нормальные алгорифмы Маркова
- 11. Машина Тьюринга алфавит: A = {a1, a2,…, aN} A = {0, 1, ◻} пробел бесконечная лента
- 12. Что такое автомат? Автомат – это устройство, работающее без участия человека. Состояние – промежуточная задача, которую
- 13. Программа для машины Тьюринга Программа состоит из команд: записать символ ai в текущую ячейку переместить каретку
- 14. Программа для машины Тьюринга Задача. На ленте записано число в двоичной системе счисления. Каретка находится где-то
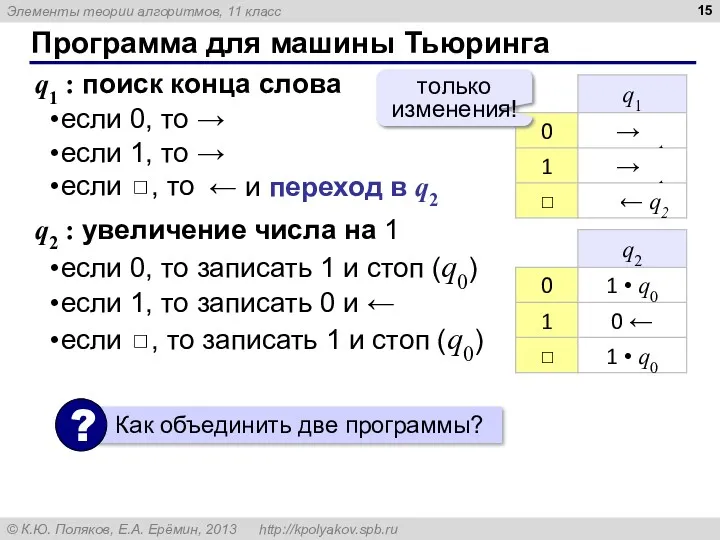
- 15. Программа для машины Тьюринга q1 : поиск конца слова если 0, то → если 1, то
- 16. Программа для машины Тьюринга Если алгоритмы А и Б можно запрограммировать на машине Тьюринга, то и
- 17. Программа для машины Тьюринга ( 0, q1, 0, →, q1 ) ( 1, q1, 1, →,
- 18. Программы для машины Тьюринга
- 19. Программы для машины Тьюринга Задача 1. Уменьшить двоичное число на 1. Задача 2. Увеличить на единицу
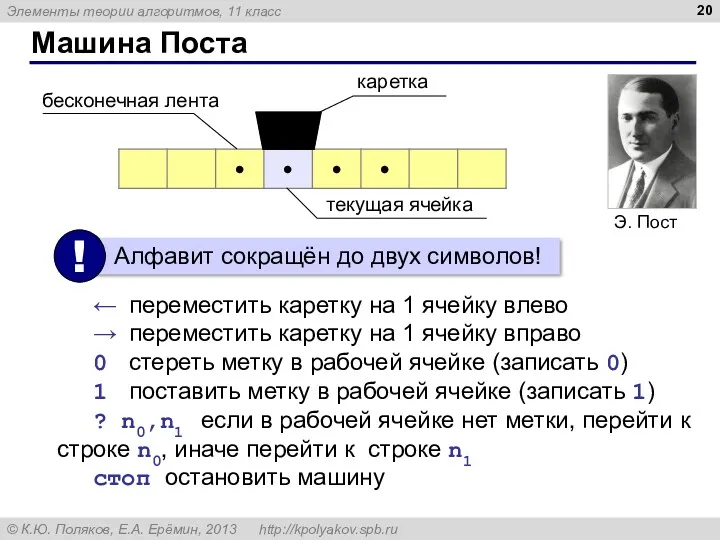
- 20. Машина Поста ← переместить каретку на 1 ячейку влево → переместить каретку на 1 ячейку вправо
- 21. Программа для машины Поста 1. ← 2. ? 1,3 3. стоп строки нумеруются команда с переходом
- 22. Программы для машины Поста
- 23. Программы для машины Поста Задача 1. Напишите программу для машины Поста, которая увеличивает (уменьшает) число в
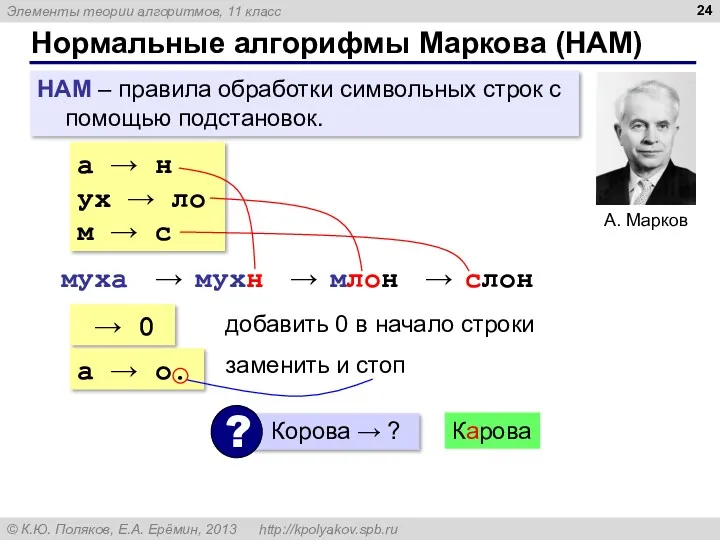
- 24. Нормальные алгорифмы Маркова (НАМ) НАМ – правила обработки символьных строк с помощью подстановок. а → н
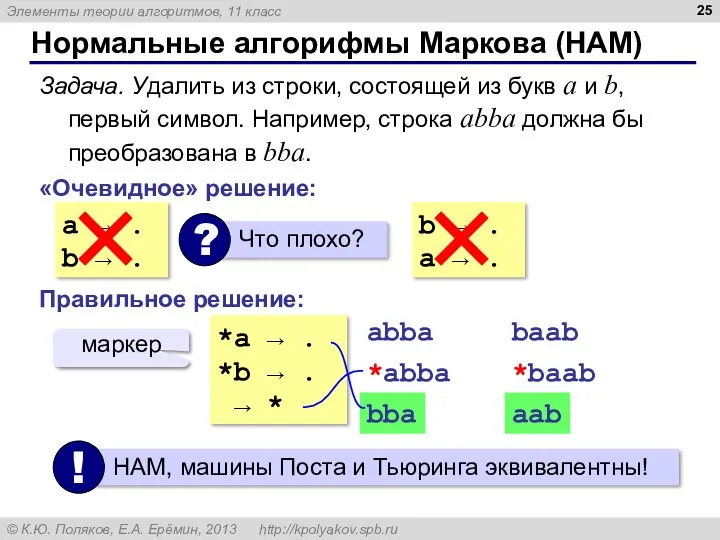
- 25. Нормальные алгорифмы Маркова (НАМ) Задача. Удалить из строки, состоящей из букв a и b, первый символ.
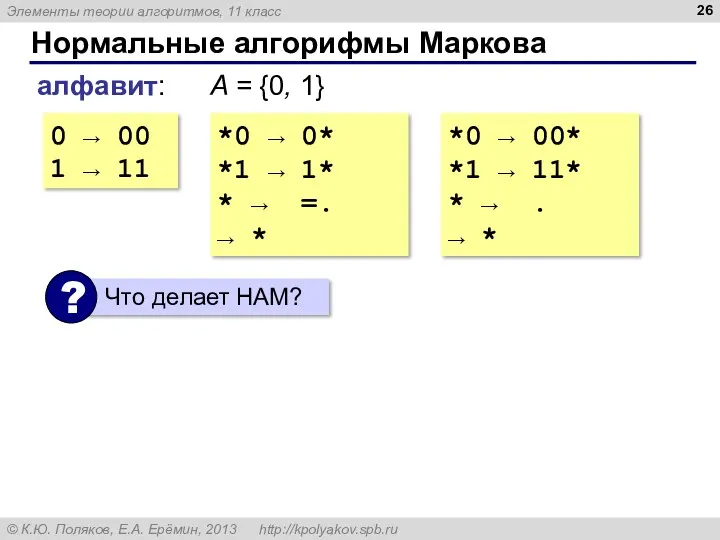
- 26. Нормальные алгорифмы Маркова 0 → 00 1 → 11 алфавит: A = {0, 1} *0 →
- 27. Нормальные алгорифмы Маркова Задача 1. Напишите НАМ, который «сортирует» цифры двоичного числа так, чтобы сначала стояли
- 28. Элементы теории алгоритмов Сложность вычислений
- 29. Что такое сложность вычислений? Задачи теории алгоритмов: существует ли алгоритм решения задачи? можно ли им воспользоваться?
- 30. Временнáя сложность T – количество элементарных операций универсального исполнителя (компьютера) Временная сложность алгоритма – функция T(n).
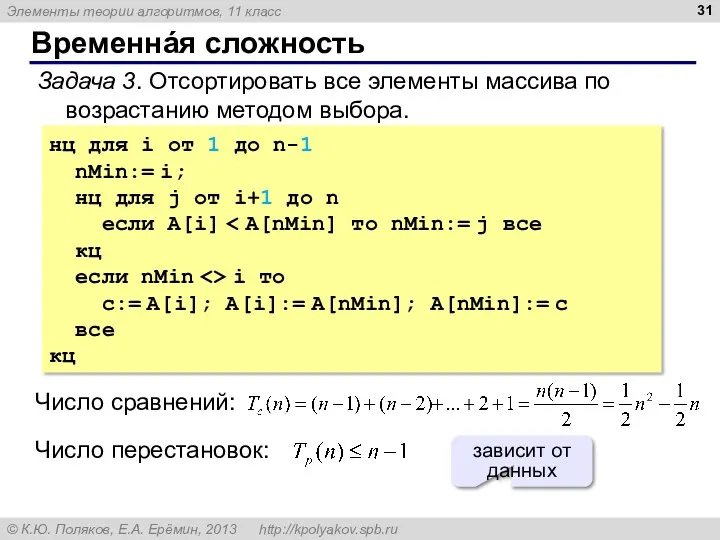
- 31. Временнáя сложность Задача 3. Отсортировать все элементы массива по возрастанию методом выбора. нц для i от
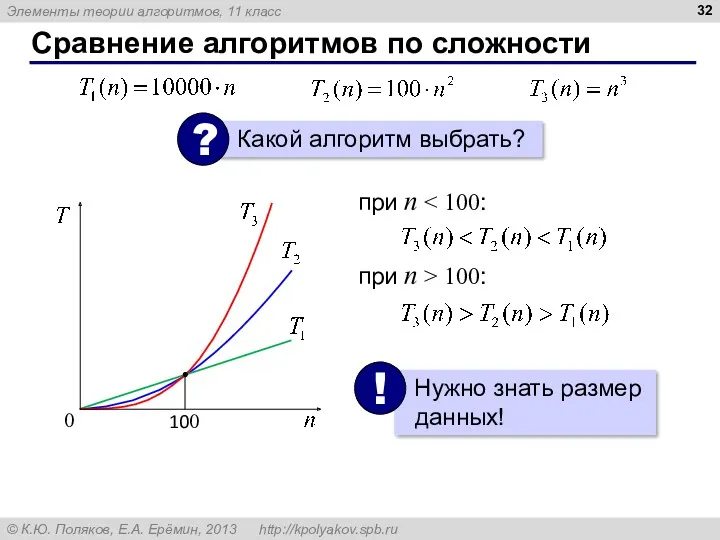
- 32. Сравнение алгоритмов по сложности при n при n > 100:
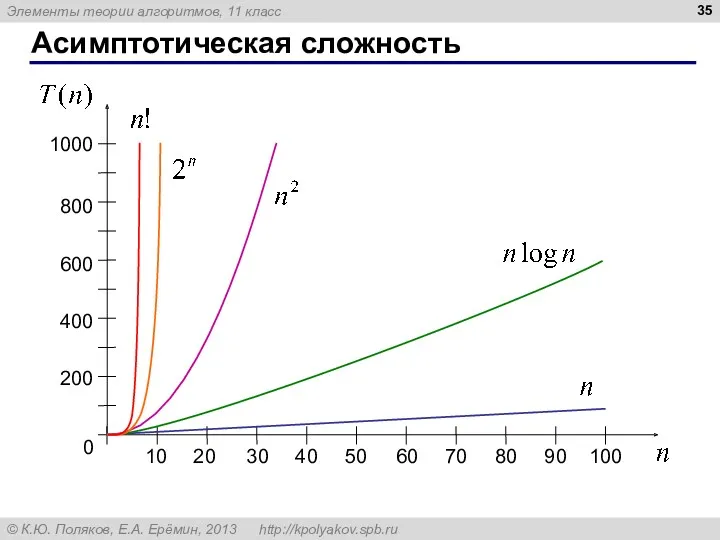
- 33. Асимптотическая сложность Асимптотическая сложность – это скорость роста количества операций при больших значениях n. сложность O(n)
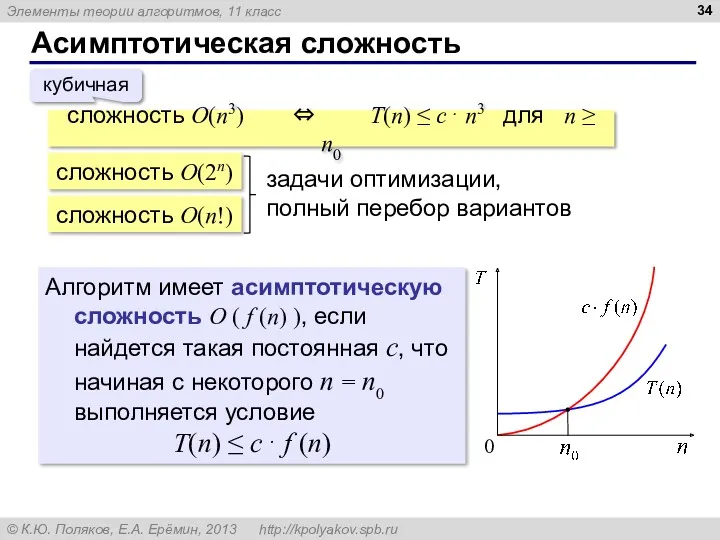
- 34. Асимптотическая сложность . сложность O(n3) ⇔ T(n) ≤ c⋅ n3 для n ≥ n0 кубичная сложность
- 35. Асимптотическая сложность
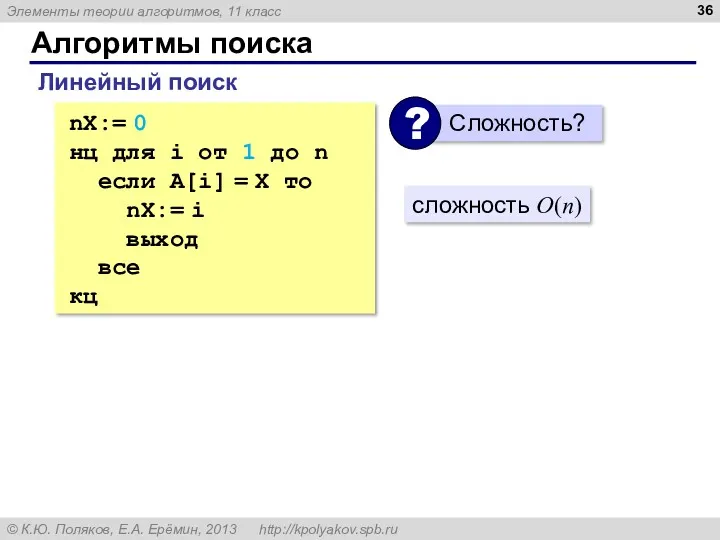
- 36. Алгоритмы поиска Линейный поиск nX:= 0 нц для i от 1 до n если A[i] =
- 37. Алгоритмы поиска Двоичный поиск L:= 1; R:= n + 1 нц пока L c:= div(L +
- 38. Алгоритмы сортировки Метод «пузырька» нц для i от 1 до n-1 нц для j от n-1
- 39. Алгоритмы сортировки Сортировка подсчётом цел C[1:MAX] нц для i от 1 до MAX C[i]:= 0 кц
- 40. Алгоритмы сортировки O(n⋅ log n) Сортировка слиянием (Merge sort) O(n⋅ log n) Пирамидальная сортировка (Heap sort)
- 41. Конец фильма ПОЛЯКОВ Константин Юрьевич д.т.н., учитель информатики ГБОУ СОШ № 163, г. Санкт-Петербург kpolyakov@mail.ru ЕРЕМИН
- 43. Скачать презентацию



























![Алгоритмы сортировки Сортировка подсчётом цел C[1:MAX] нц для i от](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/224323/slide-38.jpg)


 Гаммирование
Гаммирование Этика в интернете. 11 класс
Этика в интернете. 11 класс Кодирование информации. Двоичное кодирование
Кодирование информации. Двоичное кодирование Wireless network security
Wireless network security Базы данных. Лекция 2
Базы данных. Лекция 2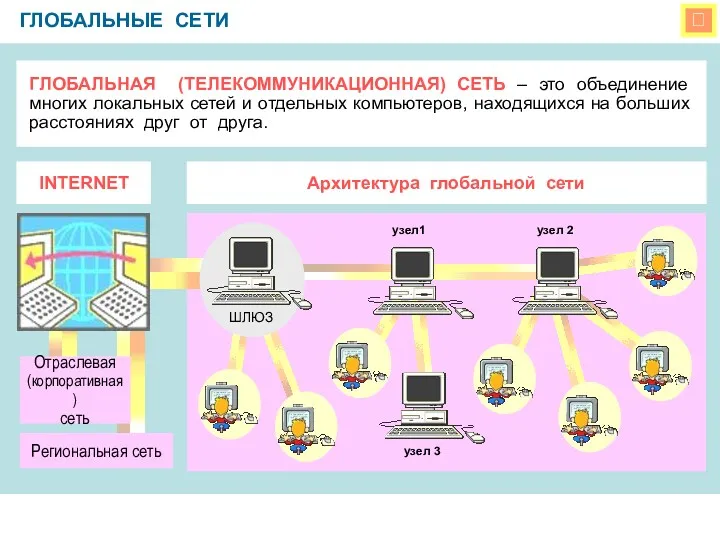 Глобальная компьютерная сеть Интернет.
Глобальная компьютерная сеть Интернет. Информационная работа в социальных сетях
Информационная работа в социальных сетях Локальные и глобальные компьютерные сети
Локальные и глобальные компьютерные сети Компьютерные сети. Основы компьютерных сетей. Технология Ethernet. Часть 1
Компьютерные сети. Основы компьютерных сетей. Технология Ethernet. Часть 1 Создание форм и отчетов в СУБД Access
Создание форм и отчетов в СУБД Access Протоколы канального уровня. Назначение канального уровня
Протоколы канального уровня. Назначение канального уровня PRO пожарики. Познавательная игра
PRO пожарики. Познавательная игра Информатика. Разделы курса
Информатика. Разделы курса Электронное учебное издание нового поколения
Электронное учебное издание нового поколения Локальна мережа ТРК Воля
Локальна мережа ТРК Воля Объектно-ориентированное программирование. Унифицированный язык моделирования UML
Объектно-ориентированное программирование. Унифицированный язык моделирования UML Информационная безопасность: основные понятия и определения
Информационная безопасность: основные понятия и определения Коллекционные компьютерные карточные игры на двоих
Коллекционные компьютерные карточные игры на двоих Жұмыста мультисервистік желілердің құрылымы
Жұмыста мультисервистік желілердің құрылымы Презентация к уроку Понятие модели и моделирование
Презентация к уроку Понятие модели и моделирование Разработка инструментального приложения для развертывания корпоративной распределенной информационной системы
Разработка инструментального приложения для развертывания корпоративной распределенной информационной системы Телекоммуникационная система. Лекция 1
Телекоммуникационная система. Лекция 1 Construct 2. Урок # 5
Construct 2. Урок # 5 Использование компьютерных технологий на уроках английского языка
Использование компьютерных технологий на уроках английского языка Глобальная компьютерная сеть интернет
Глобальная компьютерная сеть интернет Поиск игроков в команду JeyTech
Поиск игроков в команду JeyTech Виды информации по форме представления
Виды информации по форме представления Логические законы. Закон тождества
Логические законы. Закон тождества