Содержание
- 2. Во многих задачах из разных областей ставятся вопросы типа: «Сколько существует способов…», «Подсчитайте количество элементов удовлетворяющих
- 3. Решение задачи методом перебора с возвратом строится последовательным расширением частичного решения. Если на каком-то шаге такое
- 4. Рассмотрим метод перебора с возвратом. Соединение его с рекурсией определяет специфический способ реализации рекурсивных вычислений, называемый
- 5. Алгоритм поиска с возвращением Рассмотрим общий случай, когда решение задачи имеет вид вектора (а1, a2, …),
- 6. В качестве начального частичного решения берется пустой вектор () и на основе имеющихся ограничений выясняется, какие
- 7. Если частичное решение (a1, a2,…, ak-1) не предоставляет других возможностей для выбора нового ak (т.е. у
- 8. k:=1; Вычислить S1 {Например, в качестве S1 взять A1}; While k>0 do Begin While не пусто
- 9. Более коротко общую процедуру поиска с возвращением можно записать в рекурсивной форме: Procedure ПОИСК (X: вектор;
- 10. Задача о расстановке ферзей Для иллюстрации того, как описанный метод применяется при решении конкретной задачи, рассмотрим
- 11. Решение расстановки ферзей можно искать в виде вектора (a1, a2,…, a8), где ai — номер вертикали
- 12. Свободные клетки в матрице a будут равны 0, клетки «под боем» уже поставленных ферзей равны 1,
- 13. Если все ферзи расставлены, то очередное решение выводится на экран и счетчик решений k увеличивается на
- 14. program ferzi; TYPE mas=array [1..15,1..15] of integer; VAR a:mas; {матрица, описывающая положение шахматной доски} i,j,n:integer; k:longint;
- 15. PROCEDURE Fill_F(x,y:integer; var a:mas); {x, y — координаты вставки ферзя} var i, j:integer; begin for i:=
- 16. i:=x-1; {переходим в левую верхнюю клетку по диагонали} j:=y-1; {от (x,y)} while (i 0) and (j
- 17. i:=x-1; {переходим в правую верхнюю клетку} j:=y+1; while (i 0) and (j n+1) do begin a[i,j]:=1;
- 18. PROCEDURE Set_F(x:integer; a:mas); {x — строка, куда добавляем ферзя} var i,j:integer; b:mas; begin if x=n+1 then
- 19. else {в противном случае} for i:= 1 to n do {ищем в строке} if a[x,i]=0 then
- 20. BEGIN readln(n); {вводим размерность доски} k:=0; {количество вариантов расстановок равно 0} for i:= 1 to n
- 22. Скачать презентацию












![program ferzi; TYPE mas=array [1..15,1..15] of integer; VAR a:mas; {матрица, описывающая положение шахматной доски} i,j,n:integer; k:longint;](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/169741/slide-13.jpg)






 Розробка гри жанру Action-platformer з використанням Unity та штучного інтелекту
Розробка гри жанру Action-platformer з використанням Unity та штучного інтелекту Puppet – configuration management tool
Puppet – configuration management tool Class Object. Type Declarations. Class
Class Object. Type Declarations. Class Групповые операции в запросах Access
Групповые операции в запросах Access Современная структура информационных ресурсов
Современная структура информационных ресурсов Деление войск смешариков
Деление войск смешариков Технические каналы утечки персональных данных
Технические каналы утечки персональных данных Информационные технологии в системе дистанционного обучения
Информационные технологии в системе дистанционного обучения Операции и выражения в С++
Операции и выражения в С++ Создание Web-сайта. Коммуникационные технологии
Создание Web-сайта. Коммуникационные технологии Основы научных исследований. Поиск научных статей и монографий в базе данных IEEE Xplore. Тема 5
Основы научных исследований. Поиск научных статей и монографий в базе данных IEEE Xplore. Тема 5 Интернет вещей
Интернет вещей Основы научных исследований. Информационный поиск
Основы научных исследований. Информационный поиск Библиографические записи (ГОСТ Р 7.0.100-2018)
Библиографические записи (ГОСТ Р 7.0.100-2018) Модель КИМ ОГЭ по информатике в 2020 году
Модель КИМ ОГЭ по информатике в 2020 году SolidWorks. Основы работы
SolidWorks. Основы работы Создание мультимедийной презентации. Анимация
Создание мультимедийной презентации. Анимация Технологические основы цифровой экономики (облачные вычисления, большие данные и интернет вещей)
Технологические основы цифровой экономики (облачные вычисления, большие данные и интернет вещей) Перевод чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную и обратно
Перевод чисел из десятичной системы счисления в двоичную, восьмеричную и шестнадцатеричную и обратно Топ 10 инструментов. Тренды SMM 2017
Топ 10 инструментов. Тренды SMM 2017 Своя игра. Знатоки интернета
Своя игра. Знатоки интернета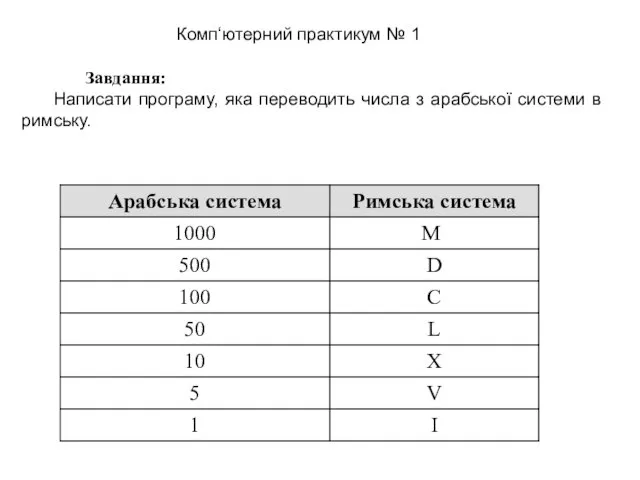 Завдання: Написати програму, яка переводить числа з арабської системи в римську
Завдання: Написати програму, яка переводить числа з арабської системи в римську Как подхватить вирус
Как подхватить вирус Графический интерфейс графического редактора Paint
Графический интерфейс графического редактора Paint Технологии передачи-2
Технологии передачи-2 Ақпараттық жүйенің түсініктемесі
Ақпараттық жүйенің түсініктемесі Предложение по работе в социальных сетях для компании Я-Такси
Предложение по работе в социальных сетях для компании Я-Такси Моделирование как метод познания
Моделирование как метод познания