Содержание
- 2. План Основні поняття та властивості дерев Бінарні дерева пошуку Обхід бінарних дерев Остовні дерева Мінімальні остовні
- 3. Умовні позначення ! - визначення - приклад - примітка - важливо! ☑ - теорема
- 4. Основні поняття та властивості дерев Дерево - це зв’язний граф без циклів. Орієнтоване дерево – це
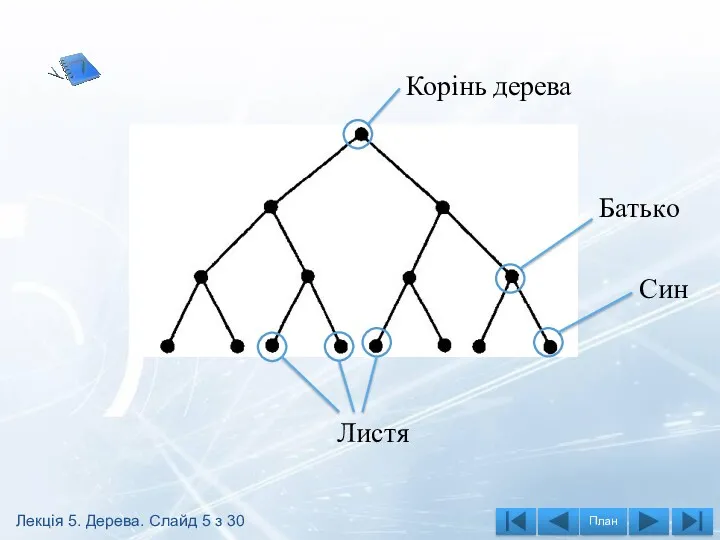
- 5. Корінь дерева Батько Син Листя Лекція 5. Дерева. Слайд 5 з 30
- 6. ТЕОРЕМА 8.1. Наступні твердження еквівалентні: а) граф G – дерево б) граф G – зв’язний і
- 7. В орієнтованому дереві рівень вершини v – це довжина шляху від кореня дерева до цієї вершини.
- 8. Лекція 5. Дерева. Слайд 8 з 30 ☑ ☑ ☑ ☑
- 9. Мають місце твердження а) Якщо е ∈ Е, то f(e) ∈ E′ (f(E) ⊆ E′) б)
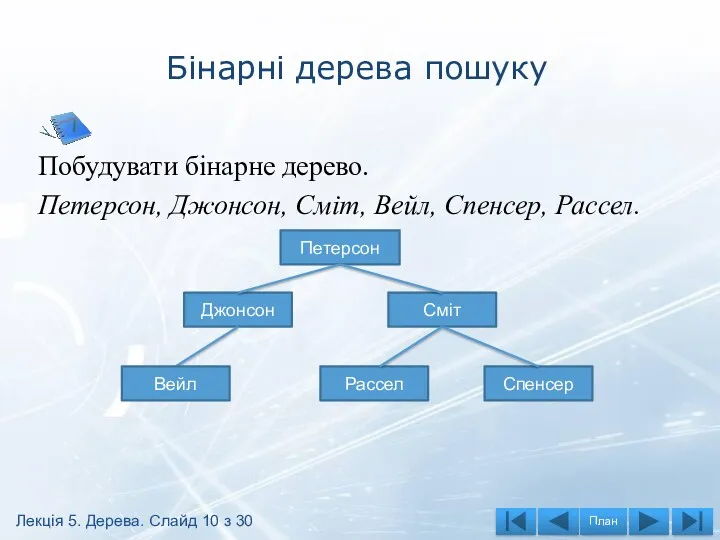
- 10. Бінарні дерева пошуку Побудувати бінарне дерево. Петерсон, Джонсон, Сміт, Вейл, Спенсер, Рассел. Петерсон Джонсон Сміт Вейл
- 11. Алгоритм вставки елемента Починаємо з кореня Якщо елемент Якщо елемент > об’єкта в вершині, переходимо до
- 12. Алгоритм пошуку елемента Починаємо з кореня Якщо елемент Якщо елемент > об’єкта в вершині, переходимо до
- 13. Алгоритм видалення елемента Якщо вершина v0 не має синів, просто видаляємо її. Якщо вершина v0 має
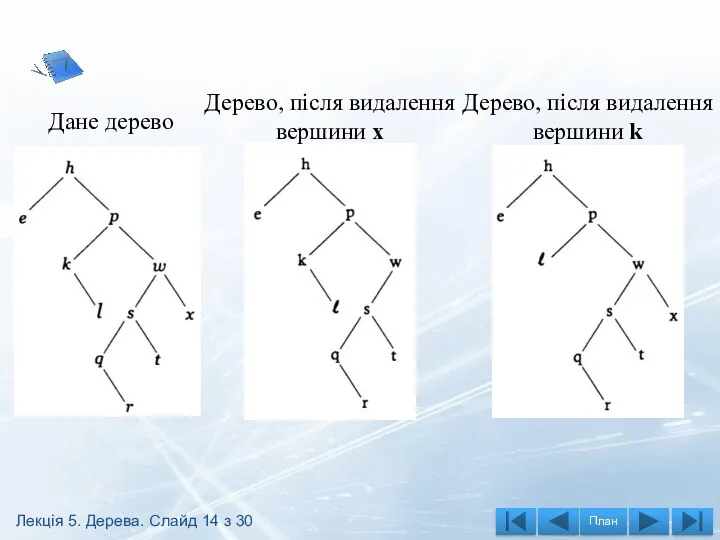
- 14. Дане дерево Дерево, після видалення вершини х Дерево, після видалення вершини k Лекція 5. Дерева. Слайд
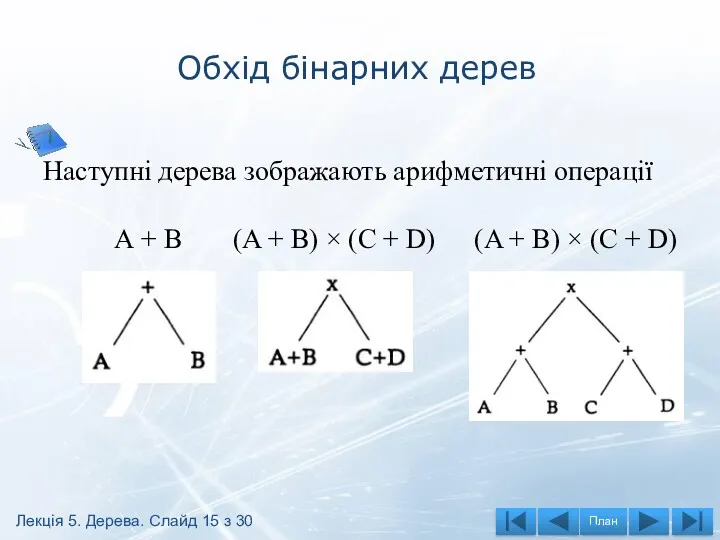
- 15. Обхід бінарних дерев Наступні дерева зображають арифметичні операції А + В (A + B) × (C
- 16. Алгоритм обходу дерева в центрованому порядку – ОЦП(корінь) Якщо ЛівийСин(корінь) існує, то ОЦП(ЛівийСин(корінь)) Обробити(корінь) Якщо ПравийСин(корінь)
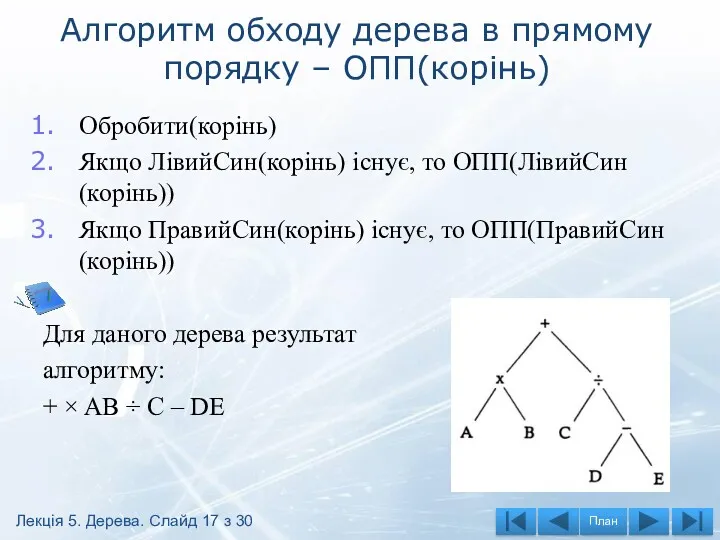
- 17. Алгоритм обходу дерева в прямому порядку – ОПП(корінь) Обробити(корінь) Якщо ЛівийСин(корінь) існує, то ОПП(ЛівийСин(корінь)) Якщо ПравийСин(корінь)
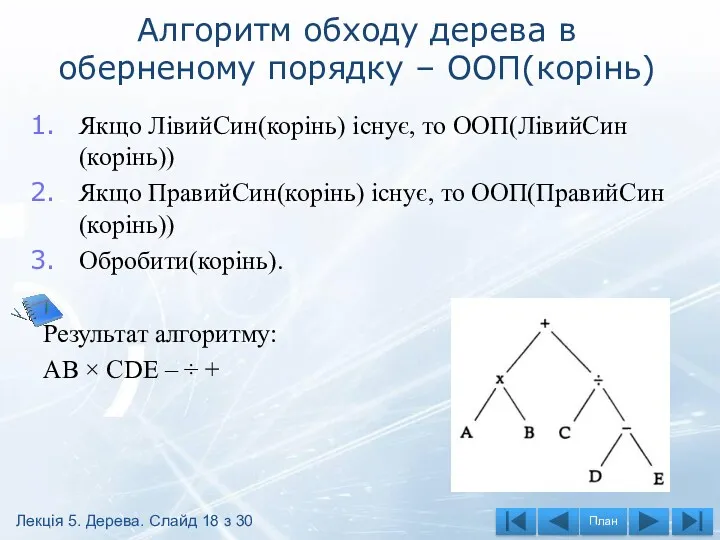
- 18. Алгоритм обходу дерева в оберненому порядку – ООП(корінь) Якщо ЛівийСин(корінь) існує, то ООП(ЛівийСин(корінь)) Якщо ПравийСин(корінь) існує,
- 19. Алгоритм перевірки ізоморфності бінарних дерев – ІБД(r1, r2) Обробити та r2. Якщо наявність(r1) = Y і
- 20. Основні дерева. Алгоритм пошуку остовного дерева в ширину – ПОДШ(G) Вибрати довільний елемент v0 графа G.
- 21. Алгоритм пошуку остовного дерева в глибину – ПОДГ (G) Помітимо кожну вершину графа G символом n.
- 22. Ліс остовних дерев називається остовним лісом. ТЕОРЕМА 8.7. Якщо Т – глибинне остовне дерево графа G(V,
- 23. Помітити v символом «використовується» Присвоїти і значення і + 1 Покласти ОР(v) = ЗС(v) = 1
- 24. Алгоритм переведення дерева в послідовність ДвП(Т) для n = 3 Для вибора а1 взяти лист vj
- 25. Алгоритм переводу послідовності в дерево – ПвД(а1, а2, …, аn-2) для n ≥ 3 Для кожного
- 26. Мінімальні остовні дерева Вага остовного дерева зваженого графа G дорівнює сумі вагів, приписаних ребрам остовного графа.
- 27. Вибрати вершину v0 графа G і ребро з найменшою вагою е1, для якого v0 – одна
- 28. Створити вагову матрицю W. Додати додатковий рядок і стовпець, щоб створити матрицю W*. В рядку 1
- 29. Література до лекції Андерсон Д.А. Дискретная математика и комбинаторика: Пер. с англ.. – М.: Изд. дом
- 31. Скачать презентацию






















 Алгоритмы решения задач. Схемы алгоритмов
Алгоритмы решения задач. Схемы алгоритмов Оптимизация программных средств
Оптимизация программных средств Компьютерные вирусы и антивирусные программы
Компьютерные вирусы и антивирусные программы Объекты. Базы данных. Запросы
Объекты. Базы данных. Запросы e- Doctor 2.00
e- Doctor 2.00 Модель данных. I, II и III нормальные формы
Модель данных. I, II и III нормальные формы Шаблоны
Шаблоны Внедрение системы СДИ-Базис
Внедрение системы СДИ-Базис Персональный компьютер
Персональный компьютер Алгоритмы оптимизации
Алгоритмы оптимизации Содержательный и алфавитный подход к измерению информации
Содержательный и алфавитный подход к измерению информации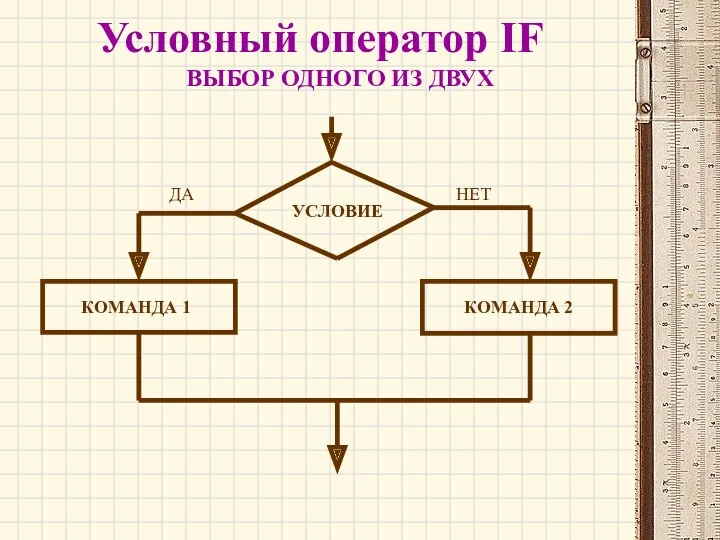 Условный оператор IF
Условный оператор IF Общие положения о штабах. Лекция №09
Общие положения о штабах. Лекция №09 Логическая и физическая организация БД. Нормальные формы, свойства нормальных форм
Логическая и физическая организация БД. Нормальные формы, свойства нормальных форм Вспомогательные алгоритмы и подпрограммы. Функции
Вспомогательные алгоритмы и подпрограммы. Функции Интернет-сайты в преподавании английского языка
Интернет-сайты в преподавании английского языка Работа с донорами. Письма донорам: технология и содержание
Работа с донорами. Письма донорам: технология и содержание Мобильный агент
Мобильный агент Проблемы и перспективы преподавания медицинской информатики на современном этапе
Проблемы и перспективы преподавания медицинской информатики на современном этапе Жанр интервью в журналистике
Жанр интервью в журналистике Изображение и звук в компьютере
Изображение и звук в компьютере Анализ и сравнение наиболее популярных СУБД для разработки веб-приложений
Анализ и сравнение наиболее популярных СУБД для разработки веб-приложений Информационное обеспечение проектной деятельности (тема 2)
Информационное обеспечение проектной деятельности (тема 2) Создание. Настройка. Редактирование. Инструмент Стена в программе ARCHICAD
Создание. Настройка. Редактирование. Инструмент Стена в программе ARCHICAD Арифметические и логические основы работы компьютера
Арифметические и логические основы работы компьютера Финансовая отчетность для владельца бизнеса. 1С:Управление небольшой фирмой 8
Финансовая отчетность для владельца бизнеса. 1С:Управление небольшой фирмой 8 Компьютерная графика
Компьютерная графика Компьютерный турнир
Компьютерный турнир