Содержание
- 2. Оптимальное дерево поиска Дано: n – количество ключей, d1 p1, p2, …, pn – частоты (вероятности),
- 3. Оптимальное дерево поиска Один из методов построения – полный перебор: n = 3, d1 = 10,
- 4. Оптимальное дерево поиска Никлаус Вирт: «Учитывая, что число возможных конфигураций из n вершин растет экспоненциально с
- 5. Оптимальное дерево поиска Никлаус Вирт: «Однако оптимальные деревья обладают одним важным свойством, которое помогает их обнаруживать:
- 6. Оптимальное дерево поиска Это позволяет разработать алгоритм, который систематически находит всё бόльшие и бόльшие поддеревья, начиная
- 7. Примеры деревьев поиска Дерево поиска, используемое в трансляторах для опознания служебных слов (есть часто используемые –
- 8. Оптимальное дерево поиска Дано: n – количество ключей, d1 p1, p2, …, pn – частоты (вероятности),
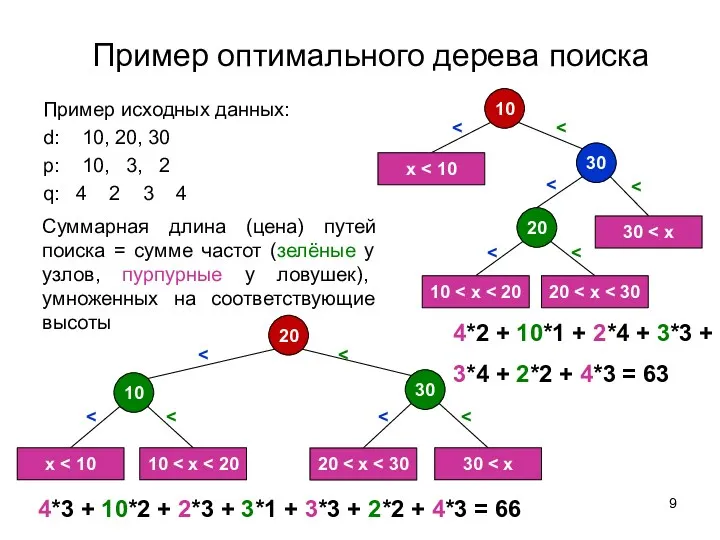
- 9. Пример оптимального дерева поиска Пример исходных данных: d: 10, 20, 30 p: 10, 3, 2 q:
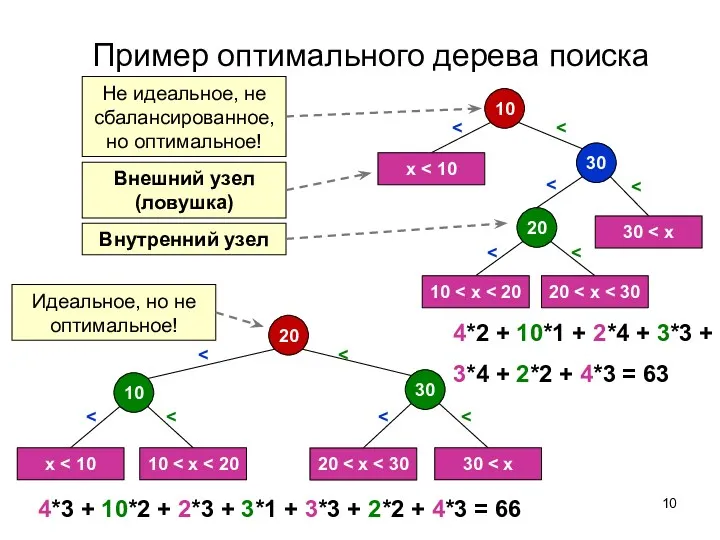
- 10. Пример оптимального дерева поиска 20 30 10 x 10 30 20 4*3 + 10*2 + 2*3
- 11. Построение оптимального дерева поиска
- 12. Построение оптимального дерева поиска Утверждение: В оптимальном дереве все поддеревья также являются оптимальными. Доказательство: Рассмотрим оптимальное
- 13. Построение оптимального дерева поиска
- 14. Построение оптимального дерева поиска
- 15. Построение оптимального дерева поиска
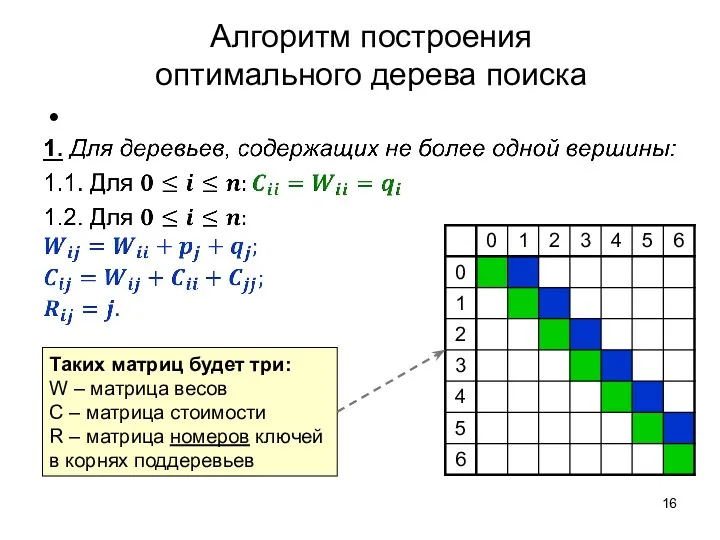
- 16. Алгоритм построения оптимального дерева поиска Таких матриц будет три: W – матрица весов C – матрица
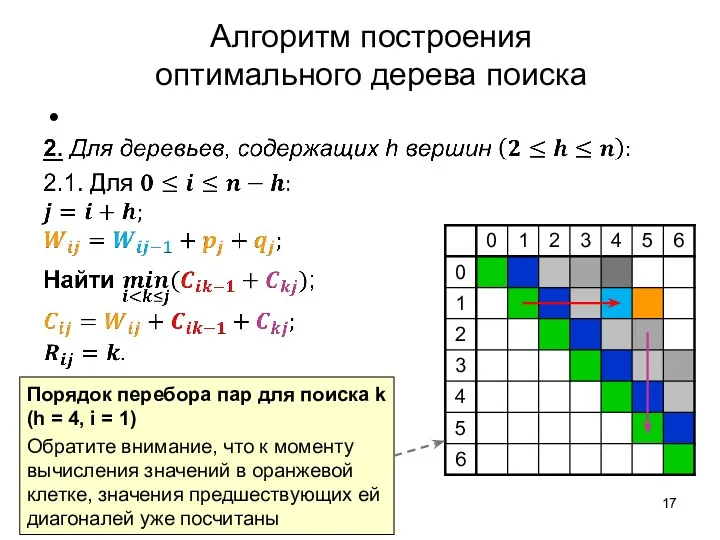
- 17. Алгоритм построения оптимального дерева поиска Порядок перебора пар для поиска k (h = 4, i =
- 18. Алгоритм построения оптимального дерева поиска Рекурсивные вызовы
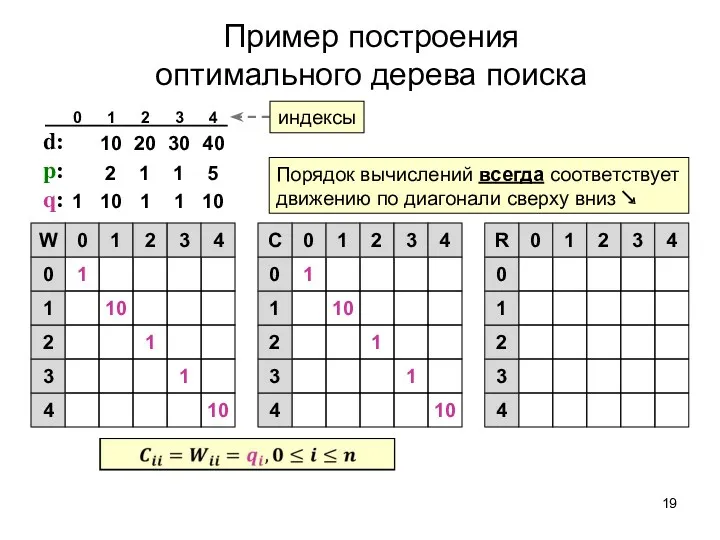
- 19. Пример построения оптимального дерева поиска d: p: q: 10 1 1 10 1 0 1 2
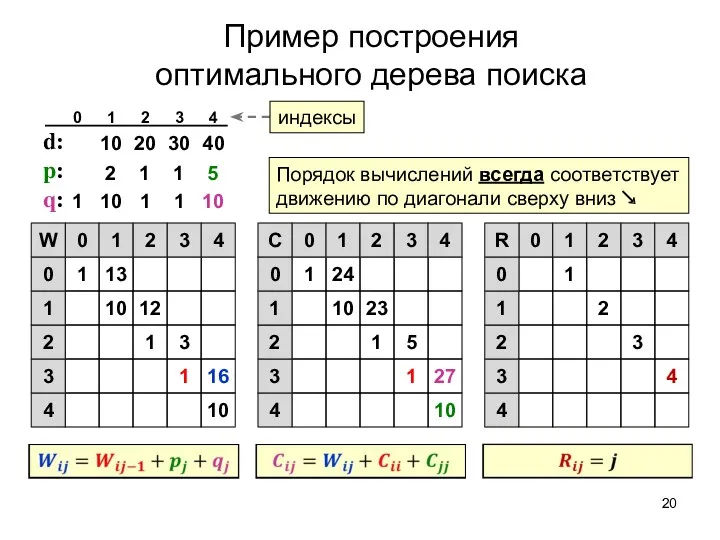
- 20. Пример построения оптимального дерева поиска d: p: q: 10 1 16 1 3 10 12 1
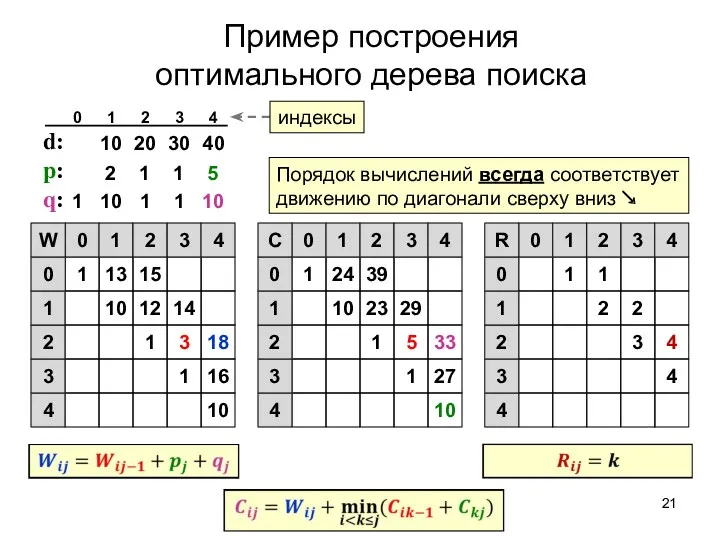
- 21. Пример построения оптимального дерева поиска d: p: q: 10 1 16 1 3 18 10 12
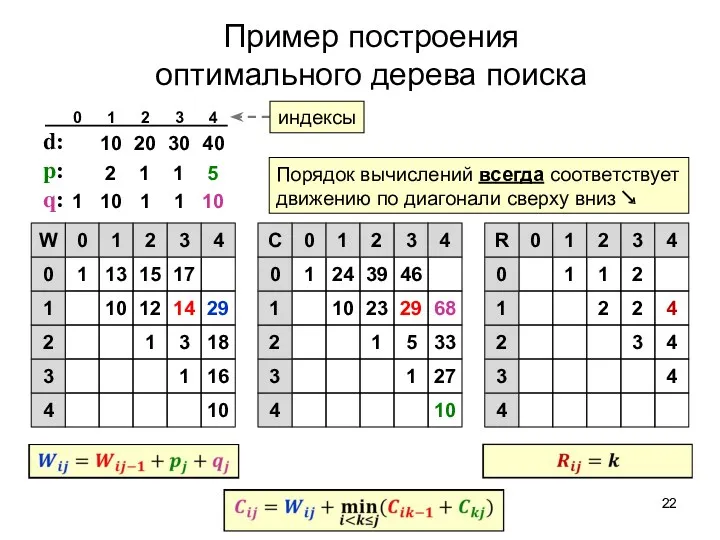
- 22. Пример построения оптимального дерева поиска d: p: q: 10 1 16 1 3 18 10 12
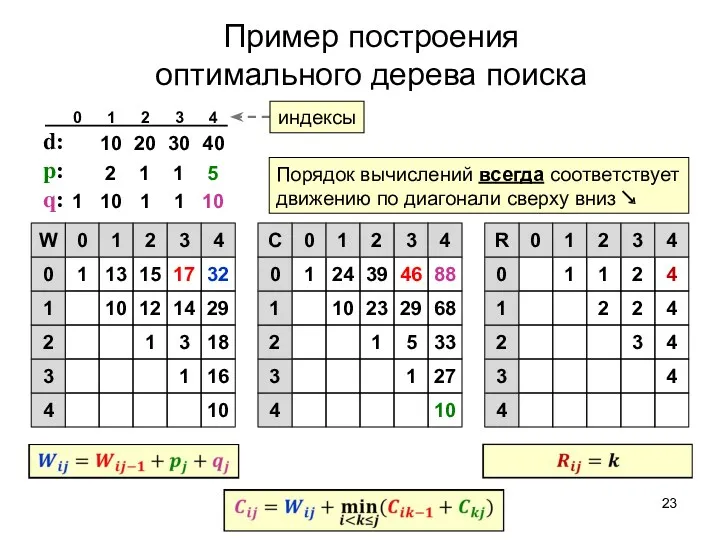
- 23. Пример построения оптимального дерева поиска d: p: q: 10 1 16 1 3 18 10 12
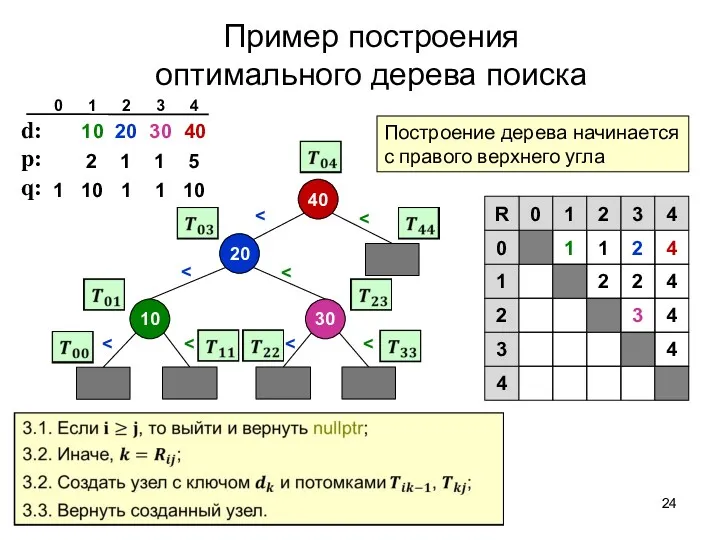
- 24. Пример построения оптимального дерева поиска 4 3 4 2 2 4 1 1 2 4 0
- 25. Алгоритмическая сложность построения оптимального дерева поиска Доказательство изложено в: Knuth, Donald E. (1971) "Optimum binary search
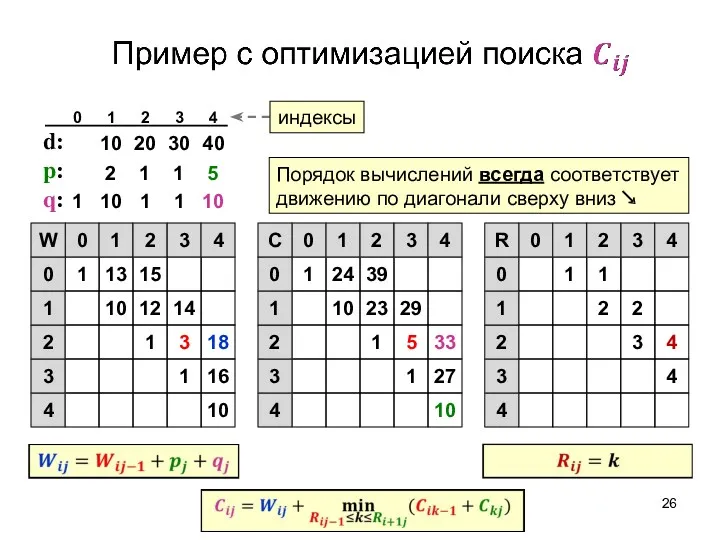
- 26. d: p: q: 10 1 16 1 3 18 10 12 14 1 13 15 0
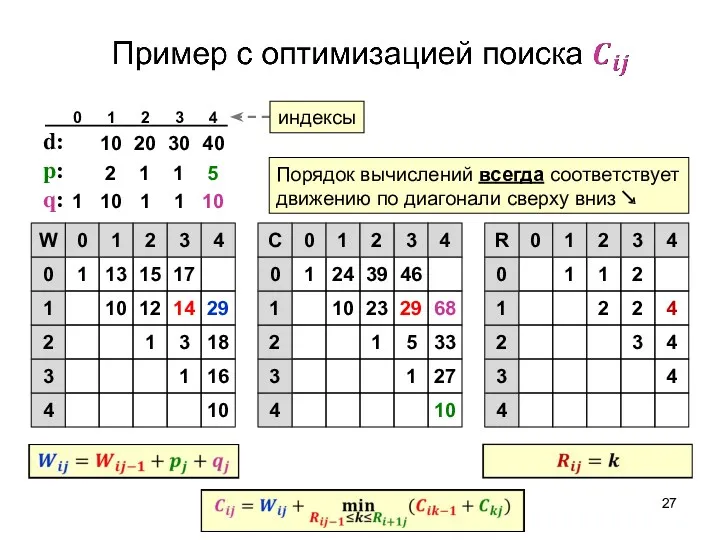
- 27. d: p: q: 10 1 16 1 3 18 10 12 14 29 1 13 15
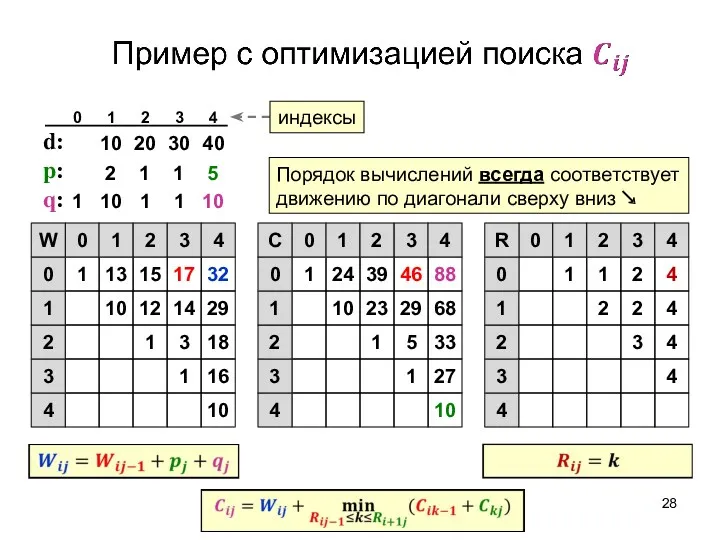
- 28. d: p: q: 10 1 16 1 3 18 10 12 14 29 1 13 15
- 30. Скачать презентацию














 Сетевой этикет
Сетевой этикет Формирование УУД при изучении графических и текстовых редакторов на уроках информатики и ИКТ
Формирование УУД при изучении графических и текстовых редакторов на уроках информатики и ИКТ Презентация Отношения между понятиями
Презентация Отношения между понятиями Публикация статей в журналах
Публикация статей в журналах Введение в операционные системы
Введение в операционные системы Информационные и управляющие системы
Информационные и управляющие системы Система управления версиями (VCS)
Система управления версиями (VCS) Принципи побудови комутаторів та комутаційних середовищ паралельних КС. (Тема 15)
Принципи побудови комутаторів та комутаційних середовищ паралельних КС. (Тема 15) Штучний інтелект: міфи і реальність
Штучний інтелект: міфи і реальність Основные понятия и определения информатики. Часть 3
Основные понятия и определения информатики. Часть 3 Информационные системы и их использование для поддержки принятия решений
Информационные системы и их использование для поддержки принятия решений Создание базы данных Автозапчасти
Создание базы данных Автозапчасти Глобальные системы бронирования
Глобальные системы бронирования Безопасность облачных технологий
Безопасность облачных технологий Вирусы и антивирусные программы
Вирусы и антивирусные программы Алгоритмы с ветвлениями
Алгоритмы с ветвлениями Шрифтовый дизайн
Шрифтовый дизайн Искусственный интеллект сегодня
Искусственный интеллект сегодня Антиплагиат. Система обнаружений текстовых заимствований в учебных и научных работах
Антиплагиат. Система обнаружений текстовых заимствований в учебных и научных работах Functions of Computers
Functions of Computers Глобальное сообщество: виртуальные связи
Глобальное сообщество: виртуальные связи Свойства логических операций. Логические законы. Решение логических задач
Свойства логических операций. Логические законы. Решение логических задач Настройка BIOS или UEFI для последующей установки операционной системы
Настройка BIOS или UEFI для последующей установки операционной системы Мультиплексоры и демультиплексоры
Мультиплексоры и демультиплексоры Самые обсуждаемые темы красноярских СМИ
Самые обсуждаемые темы красноярских СМИ Информатизация образовательного процесса
Информатизация образовательного процесса Виды компьютерной графики
Виды компьютерной графики Разработка SATA - IO-link контроллера с программными интерфейсами Legacy и AHCI
Разработка SATA - IO-link контроллера с программными интерфейсами Legacy и AHCI