Содержание
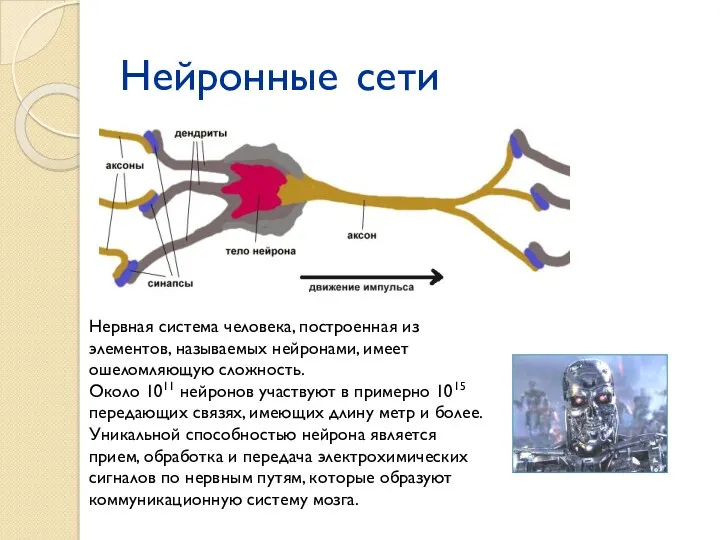
- 2. Нейронные сети Нервная система человека, построенная из элементов, называемых нейронами, имеет ошеломляющую сложность. Около 1011 нейронов
- 3. Нейронные сети Дендриты идут от тела нервной клетки к другим нейронам, где они принимают сигналы в
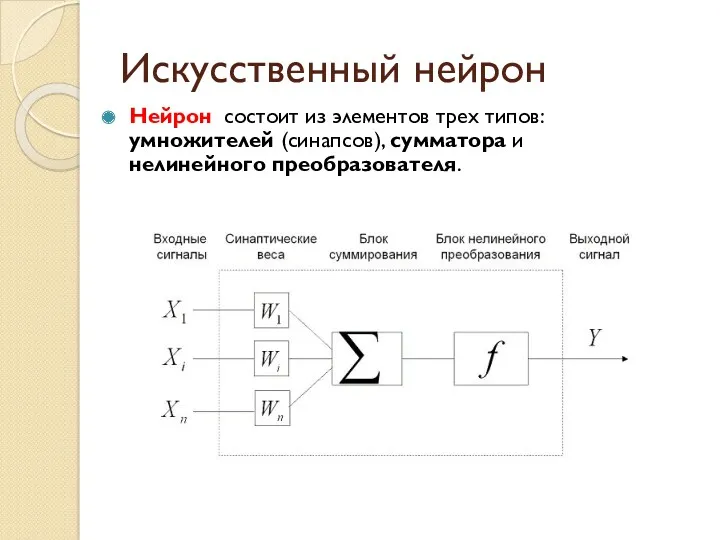
- 4. Искусственный нейрон Нейрон состоит из элементов трех типов: умножителей (синапсов), сумматора и нелинейного преобразователя.
- 5. Искусственный нейрон Синапсы осуществляют связь между нейронами, умножают входной сигнал на число, характеризующее силу связи (вес
- 6. Искусственный нейрон Алгоритм работы: нейрон получает набор (вектор) входных сигналов. в теле нейрона оценивается суммарное значение
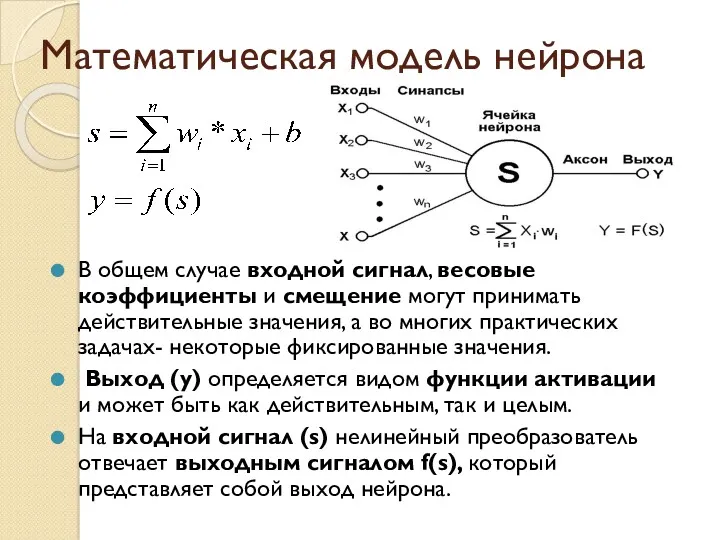
- 7. Математическая модель нейрона В общем случае входной сигнал, весовые коэффициенты и смещение могут принимать действительные значения,
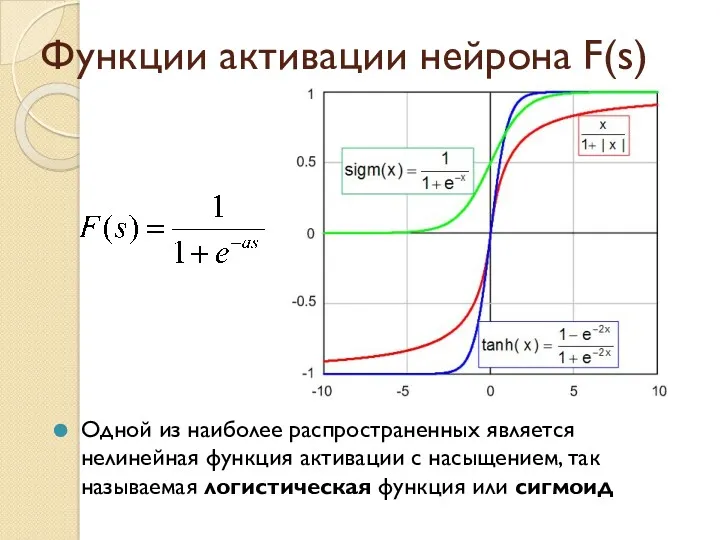
- 8. Функции активации нейрона F(s) Одной из наиболее распространенных является нелинейная функция активации с насыщением, так называемая
- 9. Функции активации нейрона F(s) При уменьшении а сигмоид становится более пологим, в пределе а=0 вырождаясь в
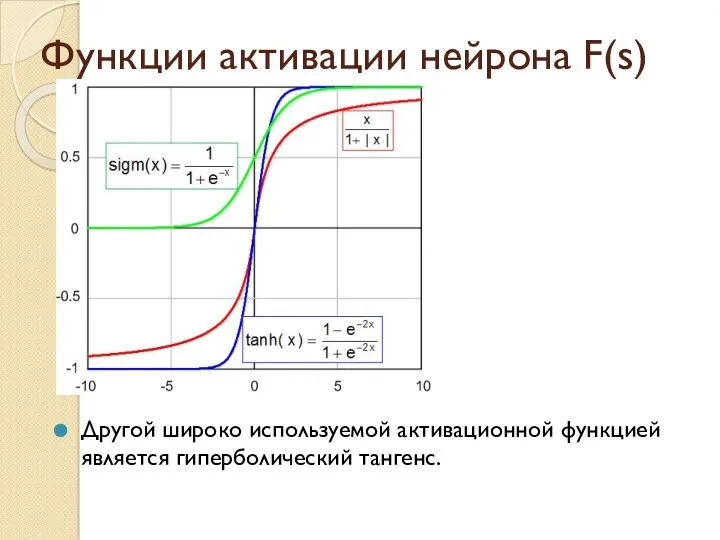
- 10. Функции активации нейрона F(s) Другой широко используемой активационной функцией является гиперболический тангенс.
- 11. Функции активации нейрона F(s) Подобно логистической функции гиперболический тангенс является s-образной функцией, но он симметричен относительно
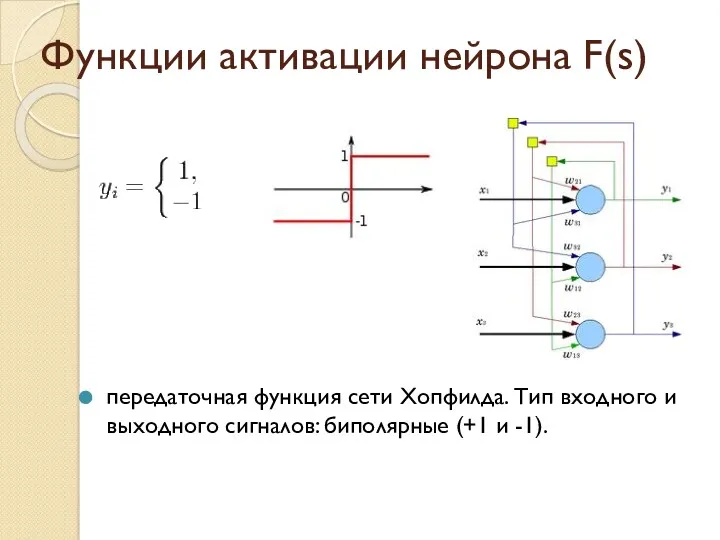
- 12. Функции активации нейрона F(s) передаточная функция сети Хопфилда. Тип входного и выходного сигналов: биполярные (+1 и
- 13. Модель нейронной сети. Персептрон. Персептро́н, или перцептрон (англ. perceptron от лат. perceptio — восприятие; нем. perzeptron)
- 14. Нейронные сети Персептрон - один слой искусственных нейронов, соединенных с помощью весовых коэффициентов с множеством входов.
- 15. Математическая модель работы нейрона в случае если F имеет вид жесткой ступеньки Работа всех сетей сводится
- 16. Математическая модель работы нейрона в случае если F имеет вид жесткой ступеньки C математической точки зрения
- 17. Математическая модель работы нейрона в случае если F имеет вид жесткой ступеньки Геометрически плоскость описывается линейным
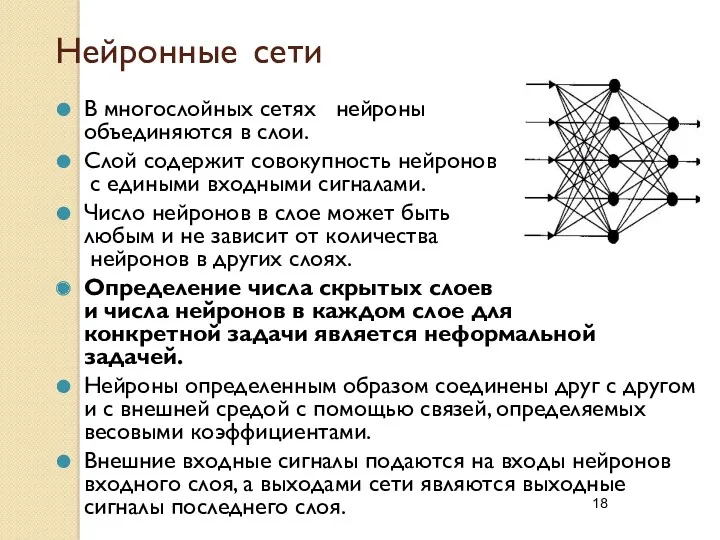
- 18. Нейронные сети В многослойных сетях нейроны объединяются в слои. Слой содержит совокупность нейронов с едиными входными
- 19. Нейронные сети Обучение НС может вестись с учителем или без него. В первом случае сети предъявляются
- 20. Нейронные сети: обучение с учителем Процесс функционирования нейронной сети зависит от величин синаптических связей (значения wij).
- 21. Нейронные сети: обучение с учителем Алгоритм обучения: ШАГ 1. Задать исходные значения весовых коэффициентов (случайные значения).
- 22. Обучение с учителем однослойного персептрона 1. Проинициализировать элементы весовой матрицы (обычно небольшими случайными значениями). 2. Подать
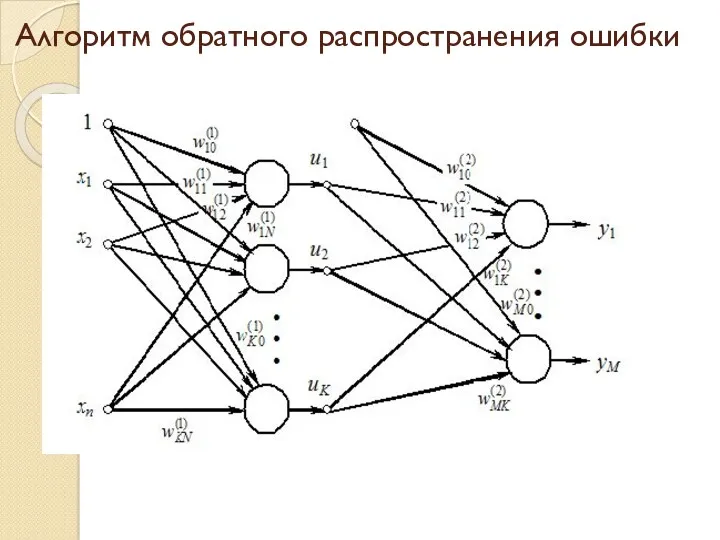
- 23. Алгоритм обратного распространения ошибки Метод обратного распространения ошибки предложен несколькими авторами независимо в 1986 г. для
- 24. Алгоритм обратного распространения ошибки
- 25. Алгоритм обратного распространения ошибки Цель обучения состоит в подборе таких значений весов и для слоев сети,
- 26. Алгоритм обратного распространения ошибки В выходном слое l-й нейрон вырабатывает выходной сигнал, определяемый как: Из формулы
- 27. Алгоритм обратного распространения ошибки Алгоритм обратного распространения ошибки - итеративный градиентный алгоритм обучения, который используется с
- 28. Алгоритм обратного распространения ошибки
- 29. Алгоритм обратного распространения ошибки
- 30. Алгоритм обратного распространения ошибки Алгоритм обратного распространения — способ ускоренного расчета компонент градиента. Идея метода в
- 31. Алгоритм обратного распространения ошибки
- 32. Алгоритм обратного распространения ошибки
- 33. Алгоритм обратного распространения ошибки
- 34. Нейронные сети Проблемы: В процессе обучения большие положительные или отрицательные значения весов могут сместить рабочую точку
- 35. Нейронные сети Проблемы обобщения и переобучения нейронной сети: Обобщение - способность нейронной сети делать точный прогноз
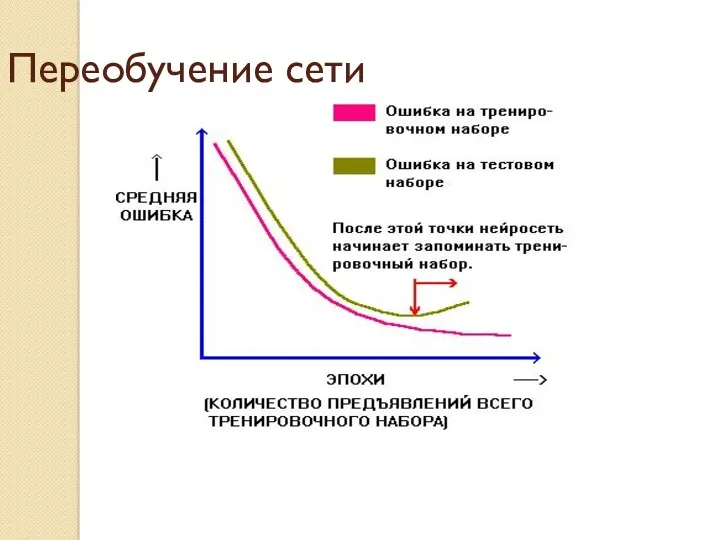
- 36. Переобучение сети
- 37. Нейронные сети Более сложная сеть дает меньшую ошибку, но это может свидетельствовать не о хорошем качестве
- 38. Нейронные сети Количество скрытых нейронов сильно зависит от количества фактов обучающей выборки. Если обучающая выборка мала,
- 39. Нейронные сети Этапы решения практических задач с использованием нейронных сетей: Формализация задачи: определение проблемы и выбор
- 40. Нейронные сети. Решение задач. Для полноценного и быстрого обучения сети наиболее значимым является адекватное представление входных
- 41. Нейронные сети Формализация задачи: определение проблемы и выбор вектора параметров
- 42. Нейронные сети Примеры формализации задач
- 43. Нейронные сети Примеры формализации задач
- 44. Нейронные сети. Решение задач.
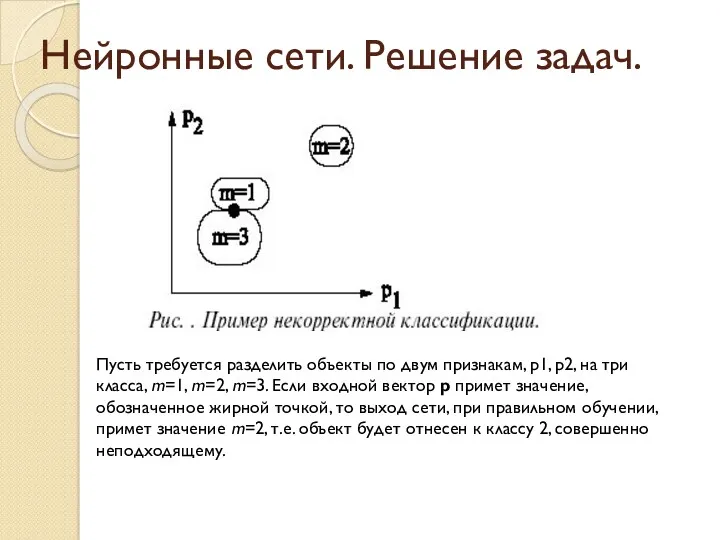
- 45. Нейронные сети. Решение задач. Пусть требуется разделить объекты по двум признакам, p1, p2, на три класса,
- 46. Нейронные сети. Решение задач. Данное явление возникает из-за того, что сеть склонна интерполировать входные и выходные
- 47. Нейронные сети. Решение задач. Пусть задана функция, определенная на интервале времени 0…t0, где t0 — текущее
- 48. Нейронные сети. Решение задач. На НС задача прогнозирования формализуется через задачу распознавания образов. Данные о прогнозируемой
- 49. Нейронные сети. Решение задач. Пусть есть данные о еженедельных продажах (k = 16): 100 94 90
- 50. Нейронные сети. Решение задач. Аппроксимация многомерной функции (восстановление значений). Рассмотрим многомерную функцию y = f(x), где
- 51. Предобработка данных Максимизация энтропии как цель предобработки
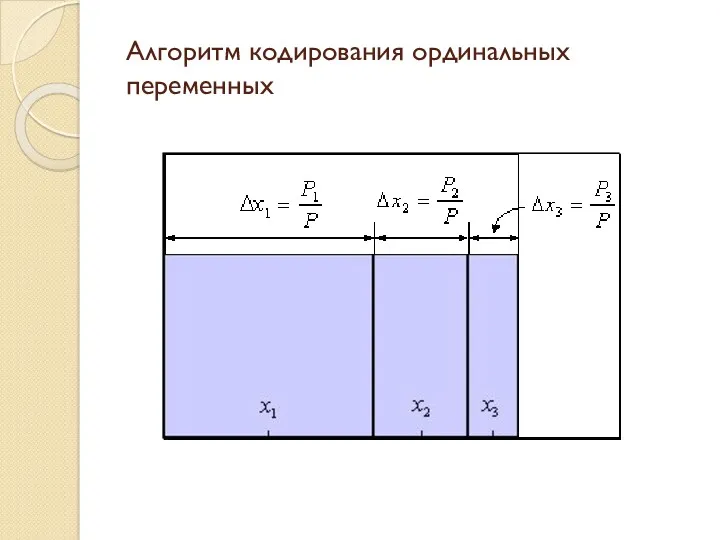
- 52. Алгоритм кодирования ординальных переменных.
- 53. Алгоритм кодирования ординальных переменных.
- 54. Алгоритм кодирования ординальных переменных
- 55. Кодирование категориальных переменных Категориальные переменные также можно закодировать как ординальные, пронумеровав их произвольным образом. Однако, такое
- 56. Нормировка и предобработка данных Как входами, так и выходами нейросети могут быть совершенно разнородные величины. Очевидно,
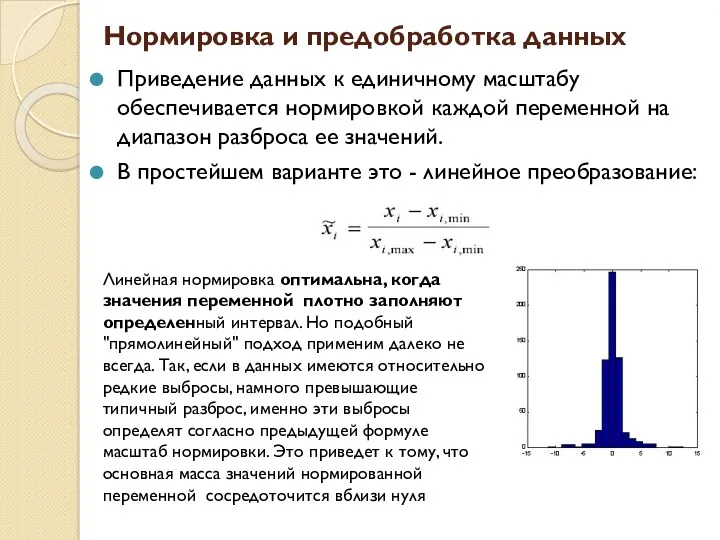
- 57. Нормировка и предобработка данных Приведение данных к единичному масштабу обеспечивается нормировкой каждой переменной на диапазон разброса
- 58. Нормировка и предобработка данных Нормировка на основе статистических характеристик данных, такие как среднее и дисперсия: Однако,
- 60. Скачать презентацию













































 Объектно-ориентированное программирование. Классы
Объектно-ориентированное программирование. Классы История письменности
История письменности Электронные образовательные ресурсы для педагогов
Электронные образовательные ресурсы для педагогов Компьютерные сети
Компьютерные сети Выражения в Access
Выражения в Access CPU How It Works
CPU How It Works Основы программирования
Основы программирования Середовище розробки. Редактори коду
Середовище розробки. Редактори коду Угрозы безопасности и их классификация. Уязвимости информационных систем. Лекция 4
Угрозы безопасности и их классификация. Уязвимости информационных систем. Лекция 4 Готовим инфографику
Готовим инфографику Система человек-машина. (Лекция 2)
Система человек-машина. (Лекция 2) Использования дистанционных технологий в образовательном процессе
Использования дистанционных технологий в образовательном процессе Информатика
Информатика Информатика в условиях реализации ФГОС в основной школе
Информатика в условиях реализации ФГОС в основной школе Sztuczna Inteligencja. (Laboratorium 6)
Sztuczna Inteligencja. (Laboratorium 6) Сценарий урока по теме Отношение входит в состав.
Сценарий урока по теме Отношение входит в состав. Prefer interfaces to reflection. (Item 53)
Prefer interfaces to reflection. (Item 53) Субъективный байесовский метод
Субъективный байесовский метод Информация и ее обработка как основа применения информационных технологий (ИТ)
Информация и ее обработка как основа применения информационных технологий (ИТ) Управление ключами в асимметричных криптосистемах. Лекция 11
Управление ключами в асимметричных криптосистемах. Лекция 11 Коллекциялар. Java
Коллекциялар. Java Электронная почта
Электронная почта Методология и технология проектирования АИС
Методология и технология проектирования АИС Работа в EXCEL.
Работа в EXCEL. Решение задач линейного программирования графическим методом
Решение задач линейного программирования графическим методом Информатика 10 класс тема Коммуникационные технологии
Информатика 10 класс тема Коммуникационные технологии Веб-дизайнер – профессия творческая
Веб-дизайнер – профессия творческая Графический редактор Paint
Графический редактор Paint