Содержание
- 2. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Для решения задач оптимизации многостадийных процессов успешно применяется метод динамического программирования - ДП, который
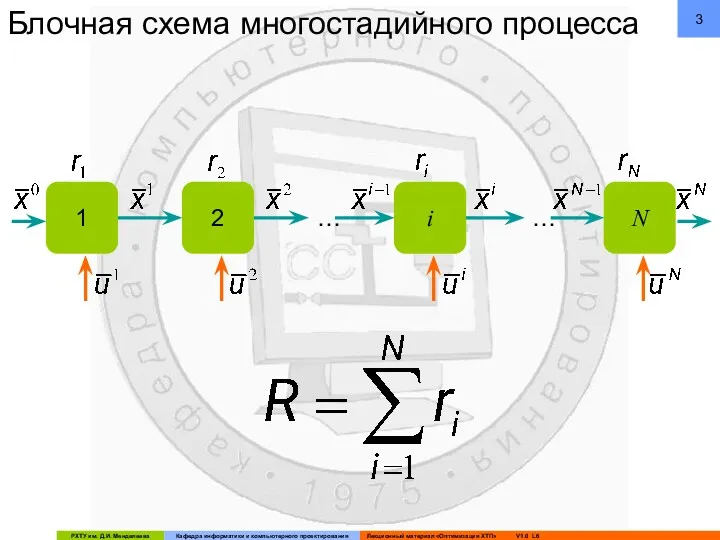
- 3. Блочная схема многостадийного процесса 1 2 … i N …
- 4. Условные обозначения на схеме каскада аппаратов: - вектор переменных состояния процесса на выходе из i-того аппарата
- 5. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Критерий оптимальности на каждой стадии определяется её состоянием:
- 6. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Уравнение математической модели для i –й стадии даёт связь между вектором входных параметров, вектором
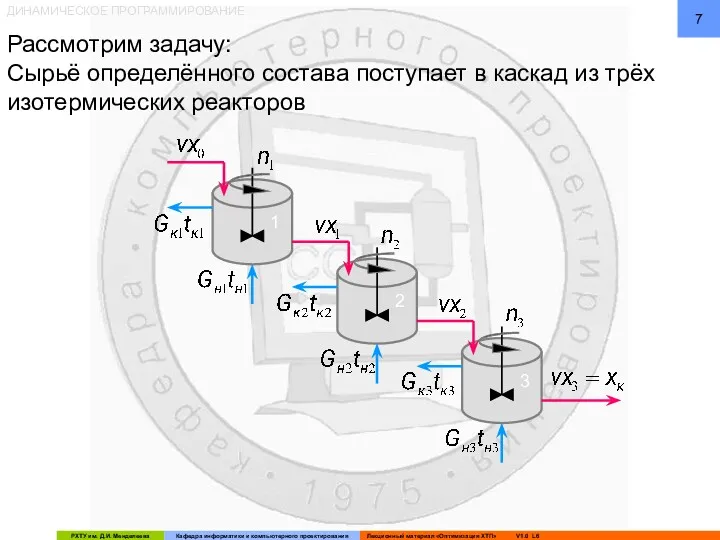
- 7. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Рассмотрим задачу: Сырьё определённого состава поступает в каскад из трёх изотермических реакторов 1 2
- 8. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ По техническому регламенту для каждого реактора допускается реализация трёх стационарных состояний, определяемых набором параметров:
- 9. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Вектор искомых управляющих переменных на каждой стадии имеет вид: n – число оборотов мешалки
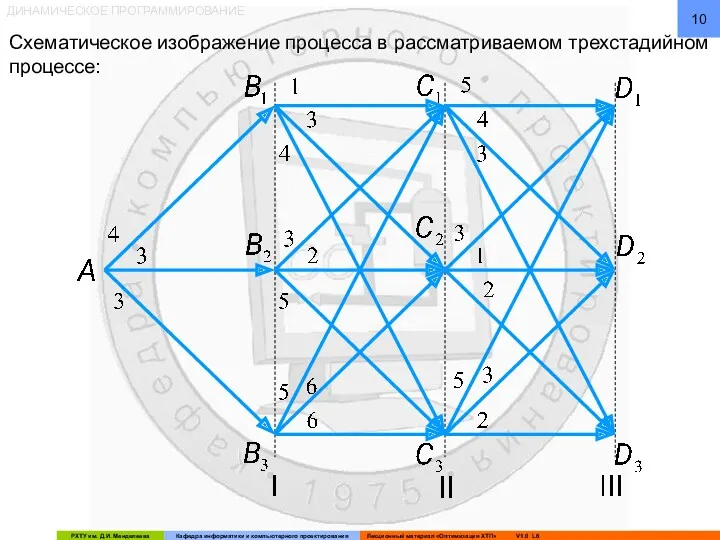
- 10. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Схематическое изображение процесса в рассматриваемом трехстадийном процессе:
- 11. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Задача оптимизации ставится следующим образом: найти такой набор управлений на каждом из реакторов, чтобы
- 12. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Точка A изображает начальное состояние процесса, которое характеризуется начальным составом сырья, его температурой и
- 13. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Далее переработка сырья во втором реакторе осуществляется таким образом, что на выходе из него
- 14. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Аналогично для третьего реактора точки D1, D2 и D3 соответствуют трём возможным стационарным состояниям
- 15. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Далее предположим, что реализация любого управления на любом реакторе связана с некоторым значением критерия
- 16. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Проще всего эта задача может быть решена обычным перебором (1-ый способ решения), т.е. сравнением
- 17. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Из всех полученных значений R выбирается максимальный и, следовательно, выбирается реализующий его набор управлений.
- 18. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Изложенный метод решения задачи требует реализации большого количества необходимых вычислений. Формула для количества возможных
- 19. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ В соответствии с принципом оптимальности, которым необходимо руководствоваться при решении таких задач, и который
- 20. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Если же задача решается изложенным методом динамического программирования (2-ой способ решения), необходимое количество вычислений
- 21. Динамическое программирование Большинство процессов химической технологии относится к классу дискретно распределённых во времени и пространстве процессов.
- 22. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Допустим, что задана конечная концентрация реагента A: Число реакторов в каскаде N. Требуется выбрать
- 23. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Критерий оптимальности является функцией многих переменных, и решение задачи методом неопределённых множителей Лагранжа становится
- 24. Формулировка принципа оптимальности Белмана Оптимальная стратегия обладает таким свойством, что каково бы ни было начальное состояние
- 25. Общая схема решения задач методом динамического программирования При подходе к решению задач оптимизации методом динамического программирования
- 26. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ При выполнении перечисленных условий необходимо правильно формулировать задачу оптимизации. При формулировке должны быть выявлены:
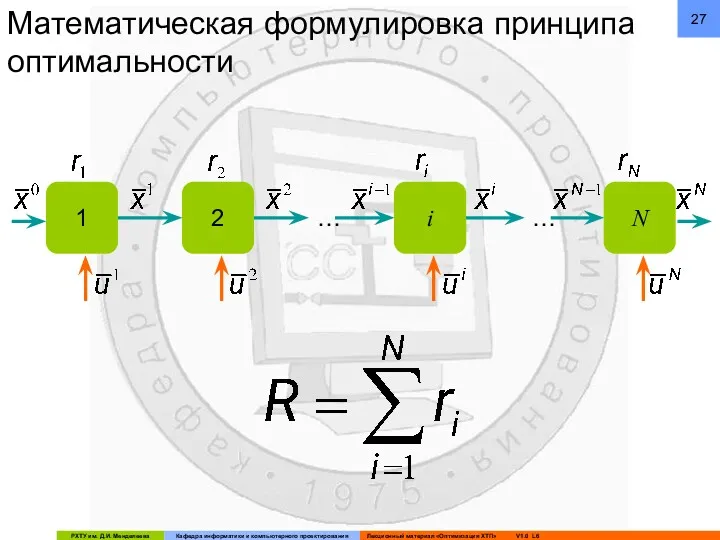
- 27. Математическая формулировка принципа оптимальности 1 2 … i N …
- 28. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Критерий оптимальности на каждой стадии определяется её состоянием:
- 29. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Уравнение математической модели для i –й стадии даёт связь между вектором входных параметров, вектором
- 30. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Решение задачи начинается с последней стадии, где необходимо выбрать оптимальное управление – так, чтобы
- 31. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Используя уравнение математической модели для данной стадии, получим: откуда определяется оптимальное управление которое зависит
- 32. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Переходя к стадии N – 1, получим условие выбора оптимального уравнения: где математическая модель
- 33. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Поскольку f1 уже выбрано, определение f2 даёт возможность выбора оптимального управления на стадии N
- 34. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Проводя аналогичный анализ, для стадии i можно записать:
- 35. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ С учётом φi получим математическую формулировку принципа оптимальности, являющуюся рекуррентной формулой, позволяющей выполнять решение
- 36. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Для первой стадии имеем: откуда определяется оптимальное управление (А) или наряду с оптимальным управлением
- 37. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ На этом завершается 1-этап решения задачи ДП. Второй этап решения Для реализация 2-этапа на
- 38. Произвольная стадия каскада
- 39. Пример 1. Пусть имеется каскад химических реакторов идеального перемешивания, в котором проводится необратимая реакция первого порядка:
- 40. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Нетрудно видеть, что в поставленной задаче оптимизации выполнены условия a, b и с: оптимизируемый
- 41. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Запишем сведения о процессе, необходимые для решения задачи оптимизации: 1. Параметрами, характеризующими состояние каждой
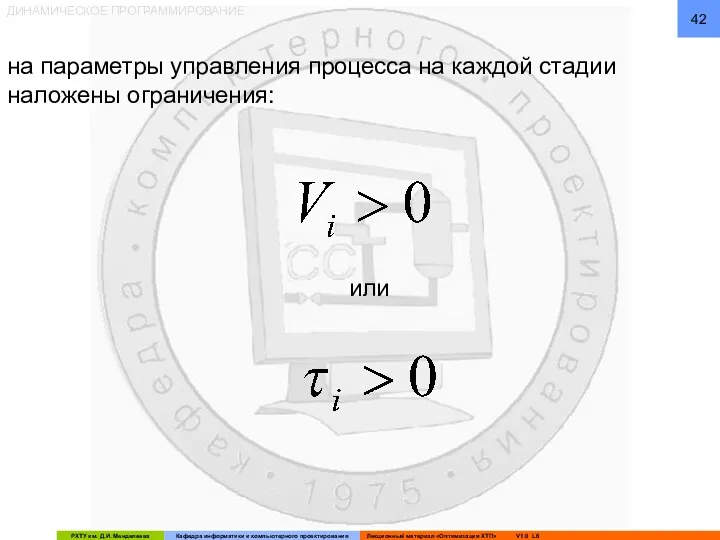
- 42. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ на параметры управления процесса на каждой стадии наложены ограничения: или
- 43. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Составляем математическое описание каждой i-ой стадии (уравнение материального баланса): или
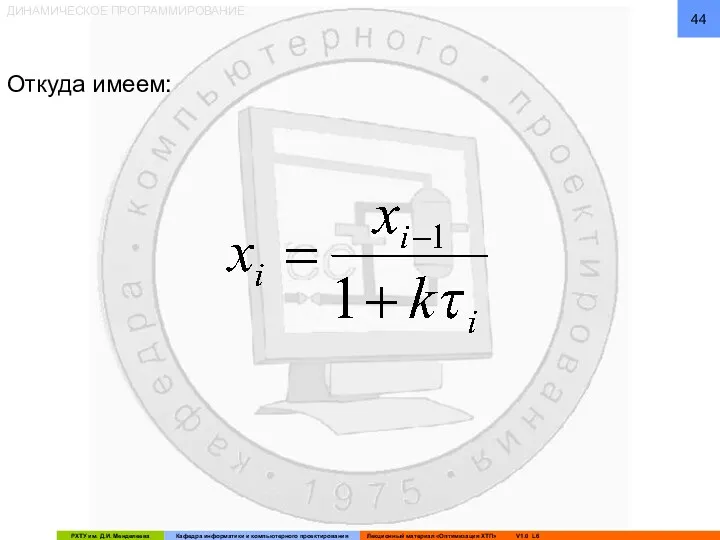
- 44. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Откуда имеем:
- 45. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Составляем критерий оптимальности (Слайд 67) : или
- 46. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Пример 1. ПЕРВЫЙ ЭТАП РЕШЕНИЯ решения выглядит следующим образом: где
- 47. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Концентрация реагента A на выходе из реактора N однозначно определяет время пребывания в нём,
- 48. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ В соответствии с общей схемой переходим к предпоследнему реактору:
- 49. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Если вид выражения критерия не сложен, а названное управление - это единственный управляющий параметр,
- 50. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ В предпоследнем реакторе необходимо выбрать такое значение x N-1, чтобы выражение в скобках имело
- 51. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Из последнего выражения следует:
- 52. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Поскольку функция f2 дифференцируемая, легко проверить достаточное условие существования экстремума: во всём диапазоне изменения
- 53. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ в точке функция f2 принимает минимальное значение. Следовательно:
- 54. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Чтобы получить минимальное значение времени пребывания в двух последних реакторах, запишем рекуррентное соотношение:
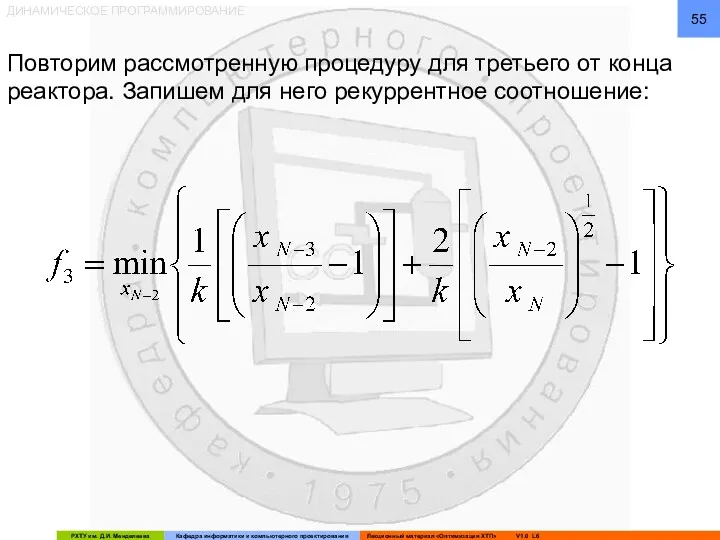
- 55. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Повторим рассмотренную процедуру для третьего от конца реактора. Запишем для него рекуррентное соотношение:
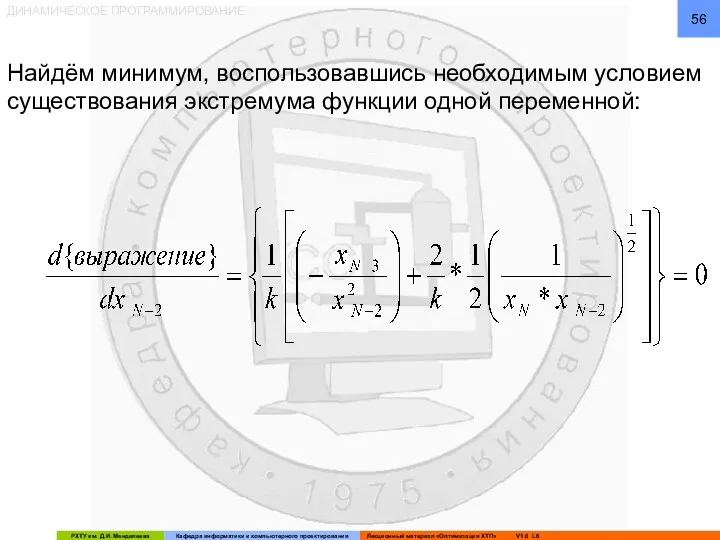
- 56. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Найдём минимум, воспользовавшись необходимым условием существования экстремума функции одной переменной:
- 57. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Откуда получаем:
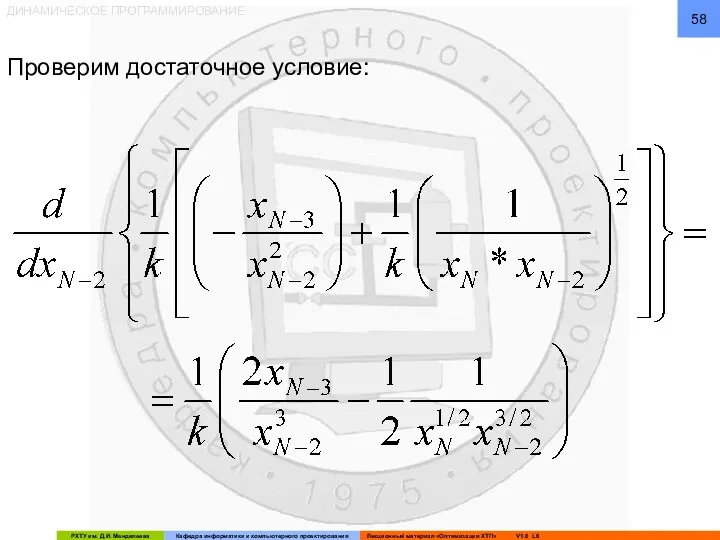
- 58. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Проверим достаточное условие:
- 59. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Подставив в последнее выражение полученное значение оптимальной концентрации, имеем: т.е. при оптимальном значении концентрации
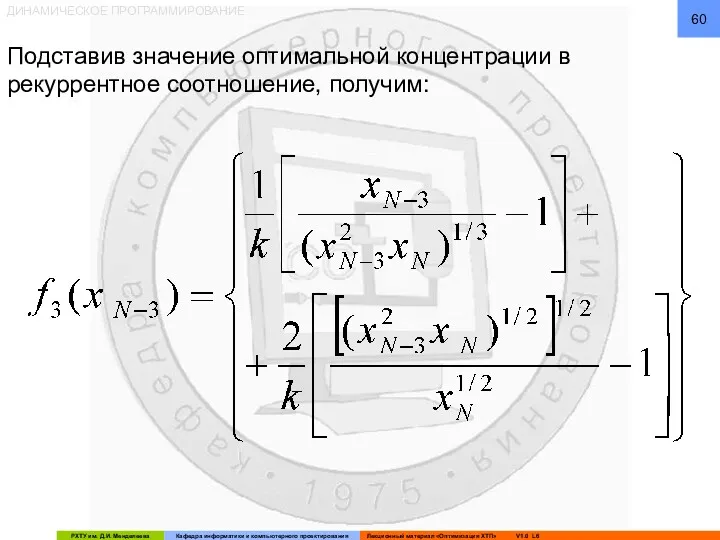
- 60. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Подставив значение оптимальной концентрации в рекуррентное соотношение, получим:
- 61. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ или после преобразований:
- 62. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Решение задачи выполняется таким же образом последовательно для всех реакторов до первого включительно. Для
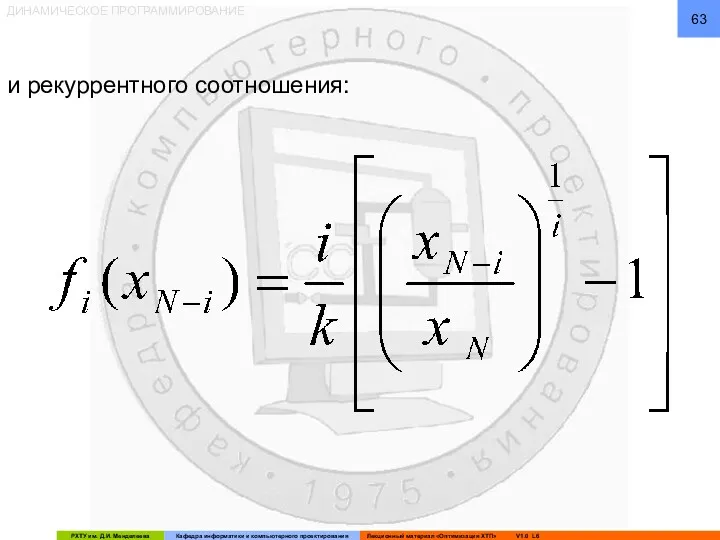
- 63. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ и рекуррентного соотношения:
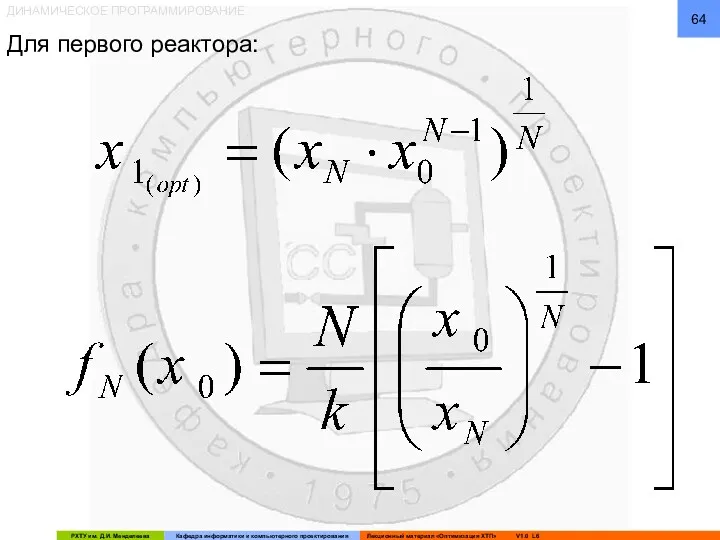
- 64. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Для первого реактора:
- 65. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Поскольку в условии задачи x 0 и xN заданы, k и N неизвестны, из
- 66. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ и для первого реактора:
- 67. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ ВТОРОЙ ЭТАП РЕШЕНИЯ На втором этапе решения из полученных соотношений определяются:
- 68. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Для второго реактора имеем:
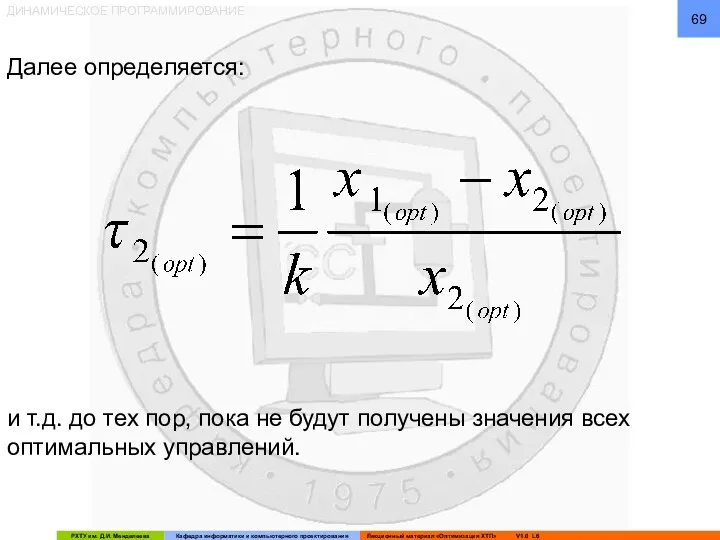
- 69. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Далее определяется: и т.д. до тех пор, пока не будут получены значения всех оптимальных
- 70. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Далее определяется: и т.д. до тех пор, пока не будут получены значения всех оптимальных
- 71. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Пример 2 В каскаде реакторов идеального перемешивания проводится простая реакция 2-го порядка : A
- 72. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Исходные данные: Число аппаратов N = 3 Начальная концентрация компонента A x0 = 1
- 73. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Решение Критерий оптимальности процесса по условию задачи есть: τi - среднее время пребывания в
- 74. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Из уравнения материального баланса для i – го реактора имеем:
- 75. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Первый этап решения Записываем рекуррентное соотношение:
- 76. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Поскольку x3 задано,
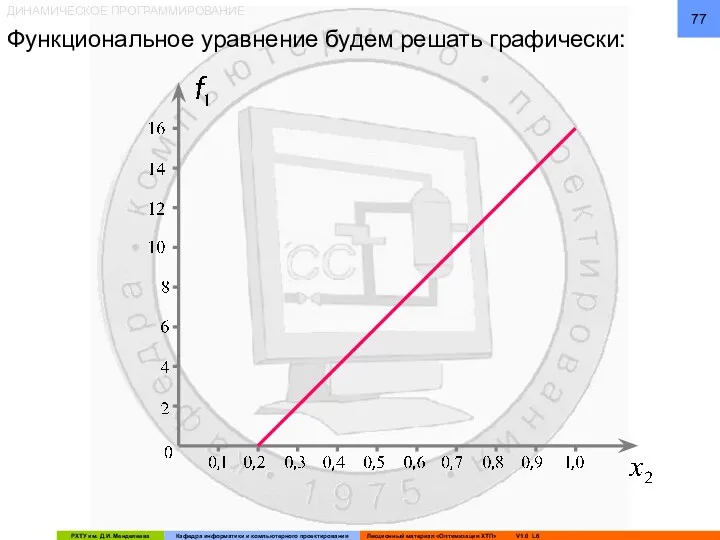
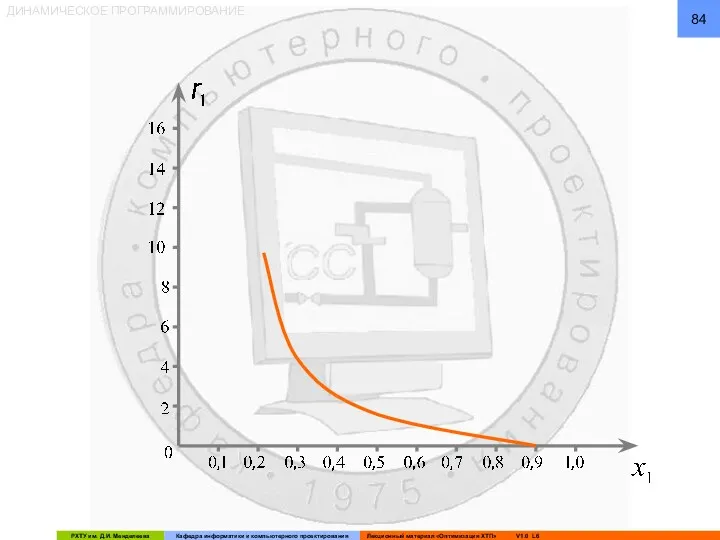
- 77. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Функциональное уравнение будем решать графически:
- 78. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Записываем рекуррентное соотношение для f2:
- 79. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 80. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 81. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 82. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 83. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Записываем рекуррентное соотношение для f2:
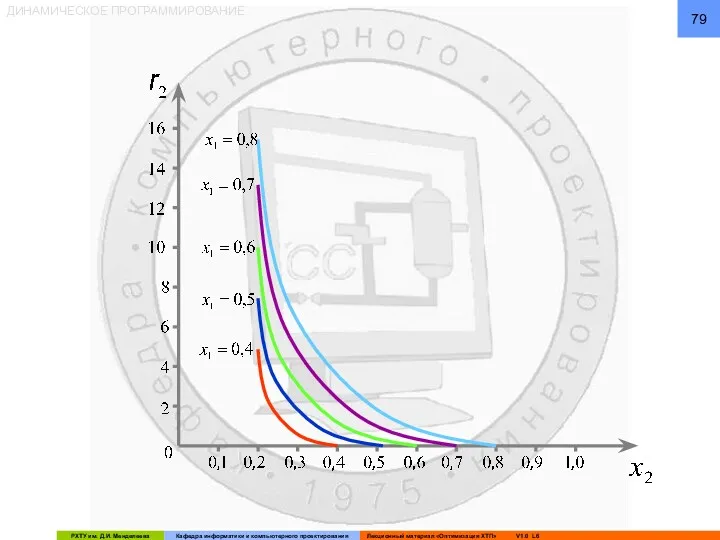
- 84. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 85. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
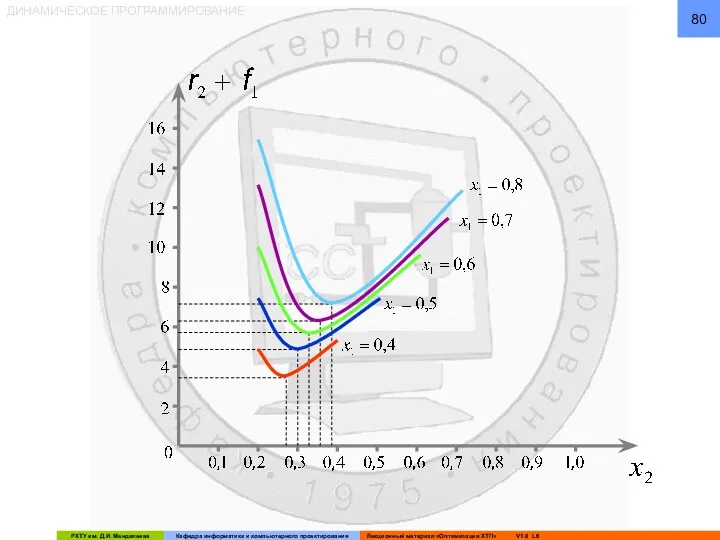
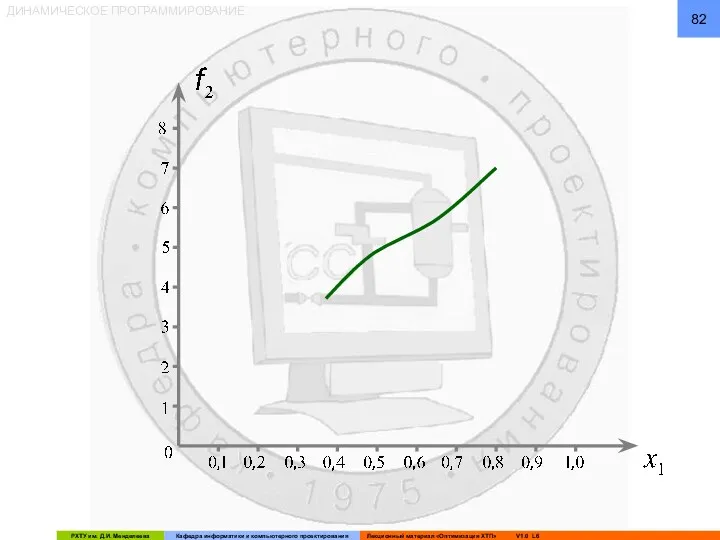
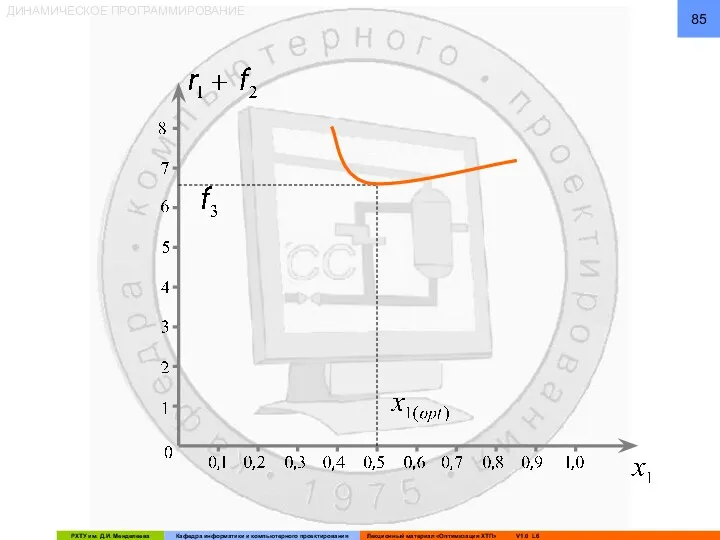
- 86. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Из графических построений определяется: И оптимальное управление, соответствующее f3: Второй этап решения
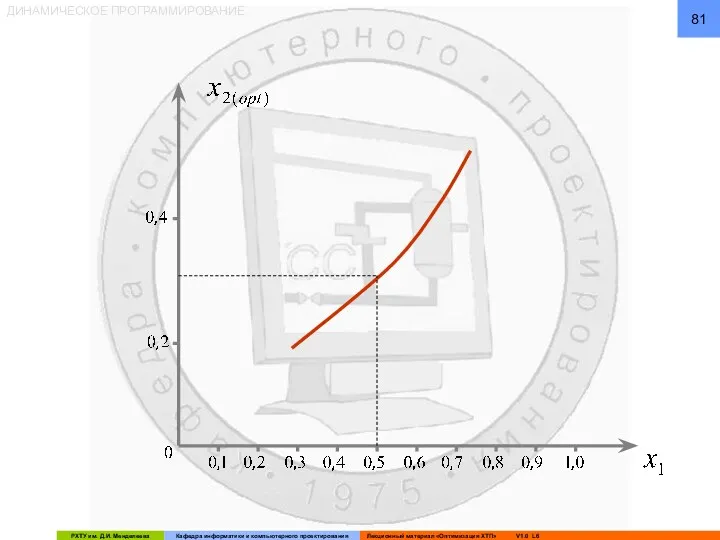
- 87. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ По найденному значению x1(opt) графически определяем x2(opt):
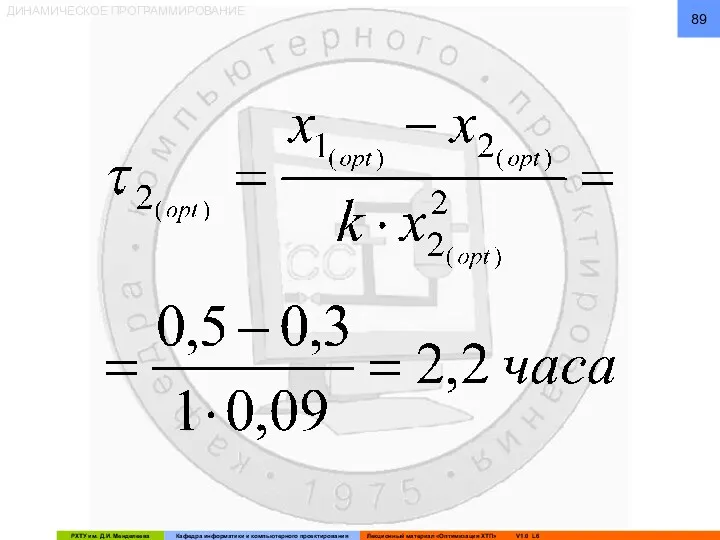
- 88. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ Рассчитываем время пребывания в каждом из аппаратов:
- 89. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 90. ДИНАМИЧЕСКОЕ ПРОГРАММИРОВАНИЕ
- 92. Скачать презентацию




































































 База данных ЭБС IPRbooks www.iprbookshop.ru
База данных ЭБС IPRbooks www.iprbookshop.ru Тетрадь по информатике Копилка заданий по формированию универсальных учебных действий
Тетрадь по информатике Копилка заданий по формированию универсальных учебных действий Электронная почта e-mail
Электронная почта e-mail Програма PowerPoint. ЇЇ можливості
Програма PowerPoint. ЇЇ можливості Університетське інтернет-телебачення
Університетське інтернет-телебачення Презентация по информатике Ввод информации с бумажных носителей
Презентация по информатике Ввод информации с бумажных носителей Қауіпсіздікті қамтамасыз ету жүесінің компонентері
Қауіпсіздікті қамтамасыз ету жүесінің компонентері Стандартные функции. Символьные операции
Стандартные функции. Символьные операции Организация работы с конфиденциальными документами
Организация работы с конфиденциальными документами Основные проблемы построения сетей
Основные проблемы построения сетей Curs 1. Mulțimi
Curs 1. Mulțimi Алгебра логики
Алгебра логики Операції і структури JavaScript. (Лекцiя 8)
Операції і структури JavaScript. (Лекцiя 8) Модернизация защищенной локальной сети института безопасности СИБГУТИ
Модернизация защищенной локальной сети института безопасности СИБГУТИ Проект информатизации процесса обучения
Проект информатизации процесса обучения Электронная почта. Сетевое коллективное взаимодействие. Сетевой этикет
Электронная почта. Сетевое коллективное взаимодействие. Сетевой этикет Презентация к уроку Информатики и ИКТ в 9-м классе по теме: Электронные таблицы
Презентация к уроку Информатики и ИКТ в 9-м классе по теме: Электронные таблицы Этапы моделирования
Этапы моделирования Трехмерная графика
Трехмерная графика Набор. Правила набора
Набор. Правила набора Презентация Информационная деятельность человека в историческом аспекте
Презентация Информационная деятельность человека в историческом аспекте Массивы. Строки. Пользовательские типы.(Тема 3)
Массивы. Строки. Пользовательские типы.(Тема 3) Тема №1 Архитектура системы команд. Занятие №2/2 Форматы команд
Тема №1 Архитектура системы команд. Занятие №2/2 Форматы команд Урок по теме: Практическая работаПостроение диаграмм различных типов в табличном процессоре Open Office org Calc
Урок по теме: Практическая работаПостроение диаграмм различных типов в табличном процессоре Open Office org Calc Програмне забезпечення вбудованого процесора турнікета для метрополітену (курсова робота)
Програмне забезпечення вбудованого процесора турнікета для метрополітену (курсова робота) Виртуальная и дополненная реальность
Виртуальная и дополненная реальность Развитие общества в контексте развития информационных технологий
Развитие общества в контексте развития информационных технологий Обработка информации. Разнообразие задач обработки информации. Информатика. 5 класс
Обработка информации. Разнообразие задач обработки информации. Информатика. 5 класс