Содержание
- 2. O mulțime este o colecție neordonată de obiecte oarecare bine determinate și distincte. Obiectele colecției se
- 3. Faptul că un obiect este element al unei mulțimi se notează prin „∈” sau „∍” (simbolul
- 4. Prin enumerarea elementelor mulțimii: {0, 1, 2}; {0, 1, 2, ...}; {...,−2,−1, 0, 1, 2, ...};
- 5. N – mulțimea numerelor naturale; Z – mulțimea numerelor întregi; Q – mulțimea numerelor raționale; I
- 6. Exemple. Enumerați elementele mulțimilor următoare: {x ∈ N : x2 {x ∈ N : x este
- 7. Mulțimea care nu conține nici un element se numește mulțimea vidă şi se notează prin ∅
- 8. Fie A o mulțime arbitrară. Familia tuturor submulțimilor din A se numește mulțimea putere a lui
- 9. Spunem că o mulțime A este inclusă în altă mulțime B dacă orice element din A
- 10. O mulțime B este o submulțime proprie a lui A dacă orice element al lui B
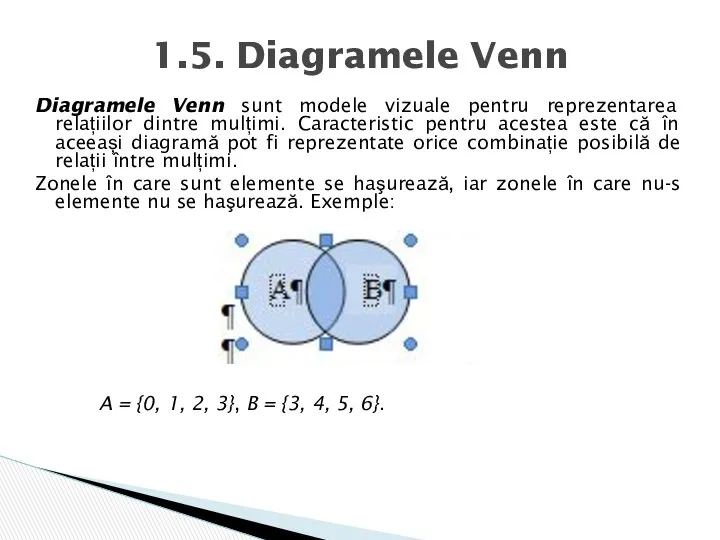
- 11. Diagramele Venn sunt modele vizuale pentru reprezentarea relațiilor dintre mulțimi. Caracteristic pentru acestea este că în
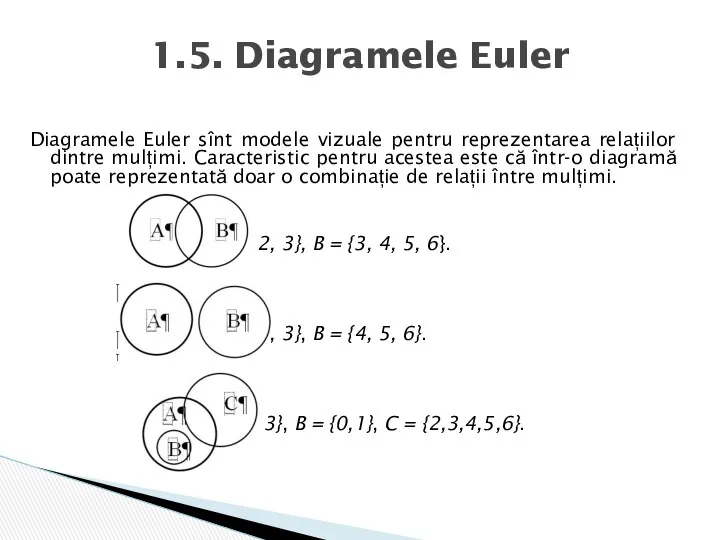
- 12. Diagramele Euler sînt modele vizuale pentru reprezentarea relațiilor dintre mulțimi. Caracteristic pentru acestea este că într-o
- 13. O operație * este bine definită dacă valoarea a * b există întotdeauna şi este unică.
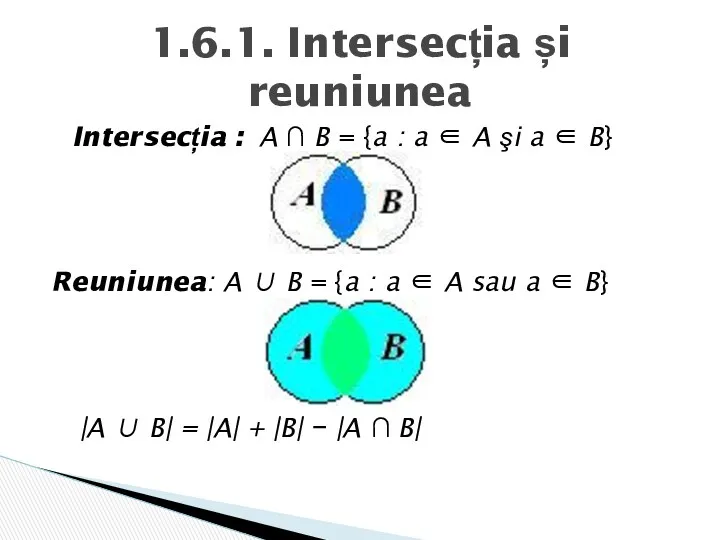
- 14. Intersecția : A ∩ B = {a : a ∈ A şi a ∈ B} Reuniunea:
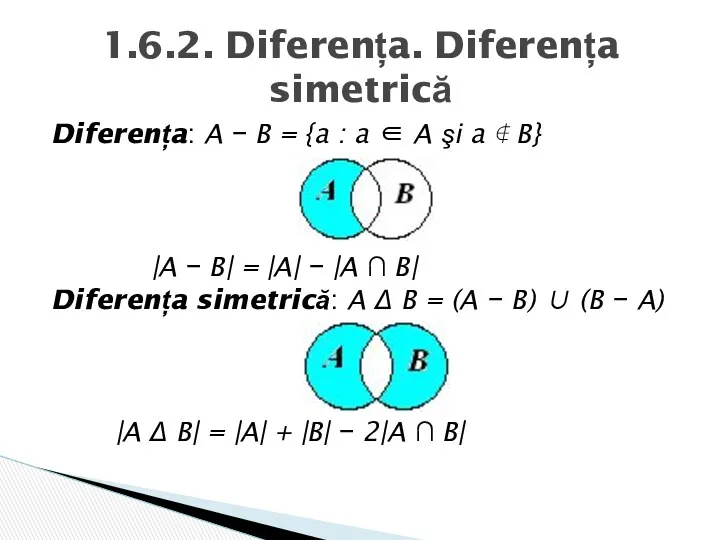
- 15. Diferența: A − B = {a : a ∈ A şi a ∉ B} |A −
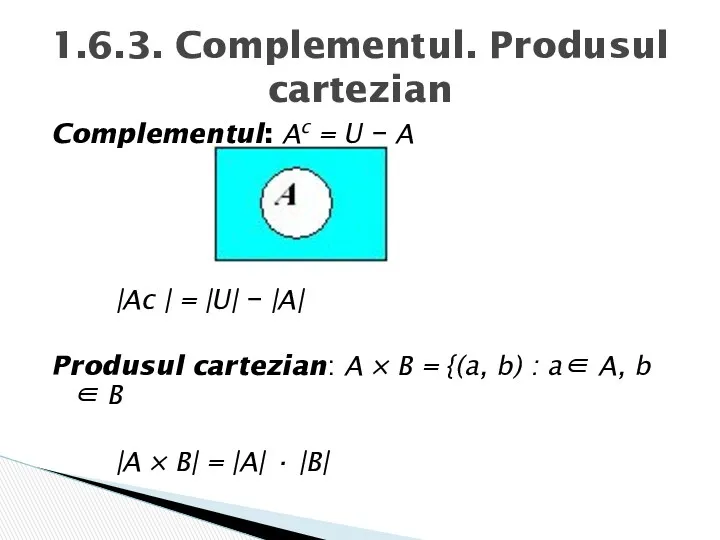
- 16. Complementul: Ac = U − A |Ac | = |U| − |A| Produsul cartezian: A ×
- 17. Fie 3 submulțimi ale U = {p, q, r, s, t, u, v, w}: A =
- 18. A1 ∩ A2 ∩ ... ∩ An = A1 ∪ A2 ∪ ... ∪ An =
- 19. 1.7. Identități cu mulțimi
- 20. 1.7. Identități cu mulțimi
- 21. În aplicații putem să ne ciocnim de necesitatea de a demonstra unele relații între mulțimi. Exemplu.
- 22. Exemplu. Să se demonstreze identitatea: (A ∪ B) \ C = (A \ C) ∪ (B
- 24. Скачать презентацию
















 Наука і техніка в інформаційному суспільстві
Наука і техніка в інформаційному суспільстві Организация ввода и вывода данных. Начала программирования
Организация ввода и вывода данных. Начала программирования Моделирование и формализация. Моделирование как метод познания
Моделирование и формализация. Моделирование как метод познания Бит чётности
Бит чётности WIC Основной рабочий инструмент
WIC Основной рабочий инструмент Графический редактор Paint
Графический редактор Paint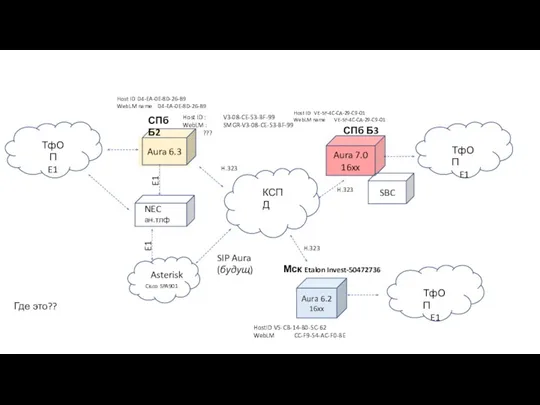 Одна распределённая станция Avaya, все сервисы через SIP. Миграция сервисов NEC и Asterisk на Avaya Aura
Одна распределённая станция Avaya, все сервисы через SIP. Миграция сервисов NEC и Asterisk на Avaya Aura Технология поиска информации в сети Интернет
Технология поиска информации в сети Интернет Построение диаграмм с использованием Мастера диаграмм при изучении текстового процессора Microsoft Word
Построение диаграмм с использованием Мастера диаграмм при изучении текстового процессора Microsoft Word Главные тренды
Главные тренды Основи Turtle. (Лекция 2)
Основи Turtle. (Лекция 2) Tег DIV и SPAN. CSS. (Тема 9)
Tег DIV и SPAN. CSS. (Тема 9) Cover title. Cover subtitile. Footer department
Cover title. Cover subtitile. Footer department Файл - серверные и клиент - серверные технологии в современных информационных технологиях
Файл - серверные и клиент - серверные технологии в современных информационных технологиях Программное обеспечение ГИС. Лекция 18
Программное обеспечение ГИС. Лекция 18 Электронные платежные системы. Лекция 9
Электронные платежные системы. Лекция 9 Мистерия Игры Богов – IV. Квадрант Мутации
Мистерия Игры Богов – IV. Квадрант Мутации Системы счисления. Двоичная, восьмеричная, шестнадцатеричная
Системы счисления. Двоичная, восьмеричная, шестнадцатеричная Информационная безопасность. Криптографические средства защиты данных. Шифрование
Информационная безопасность. Криптографические средства защиты данных. Шифрование Презентация урока по теме Двоичное кодирование информации в компьютере
Презентация урока по теме Двоичное кодирование информации в компьютере Типы алгоритмов
Типы алгоритмов Монтаж видеороликов в Windows Movie Maker
Монтаж видеороликов в Windows Movie Maker Инструкция по обеспечению актуальности данных при формировании и ведении ведомственных перечней государственных услуг и работ
Инструкция по обеспечению актуальности данных при формировании и ведении ведомственных перечней государственных услуг и работ Организация работы с одаренными и мотивированными детьми на уроке информатики
Организация работы с одаренными и мотивированными детьми на уроке информатики 8. Java Databases and JDBC 1. Introduction to Databases
8. Java Databases and JDBC 1. Introduction to Databases Как понять когда можно бросать работу и уходить в стартап
Как понять когда можно бросать работу и уходить в стартап Управление насосной станцией. Программирование в LOGO! Soft Comfort
Управление насосной станцией. Программирование в LOGO! Soft Comfort База данных магазина велозапчастей
База данных магазина велозапчастей