Содержание
- 2. ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ Логика – наука о формах и способах мышления. Основными формами мышления являются
- 3. Логика — это наука, изучающая законы и формы мышления. Алгебра логики — это математический аппарат, с
- 4. ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ Высказывание не может быть выражено повелительным или вопросительным предложением, так как оценка
- 5. ОСНОВНЫЕ ПОНЯТИЯ АЛГЕБРЫ ЛОГИКИ Поэтому высказывание можно представить некоторой переменной величиной, значением которой может быть 0
- 6. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ В основе булевой алгебры лежат 16 основных функций. Наиболее часто применяемые из них:
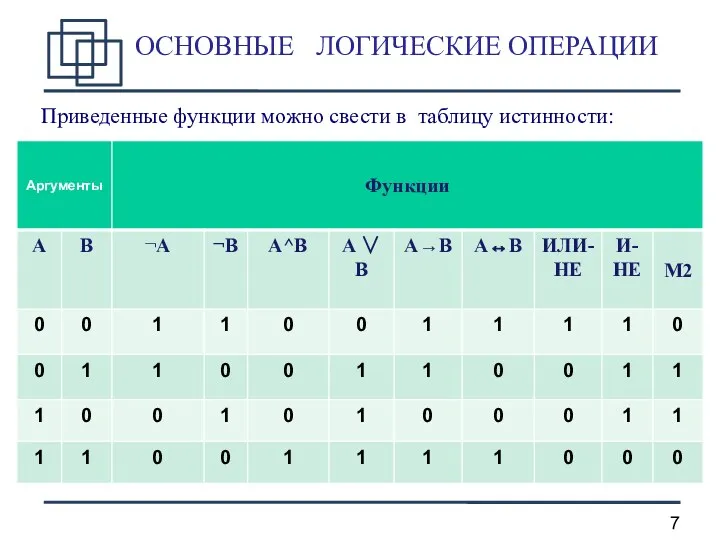
- 7. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Приведенные функции можно свести в таблицу истинности:
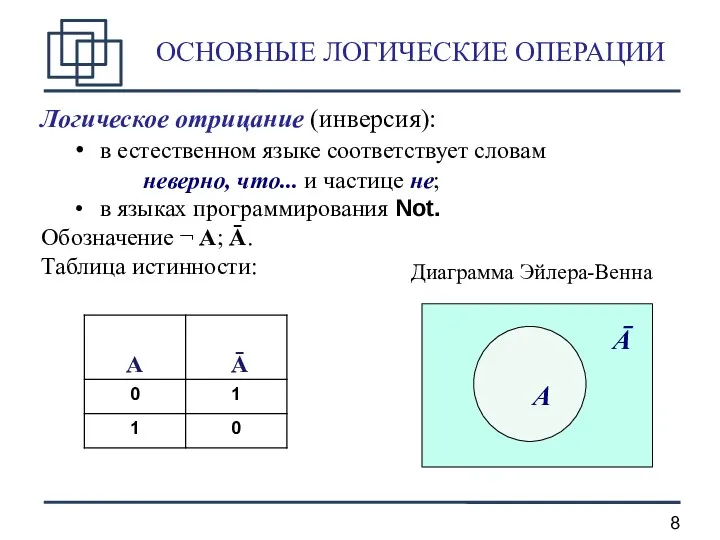
- 8. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое отрицание (инверсия): в естественном языке соответствует словам неверно, что... и частице не;
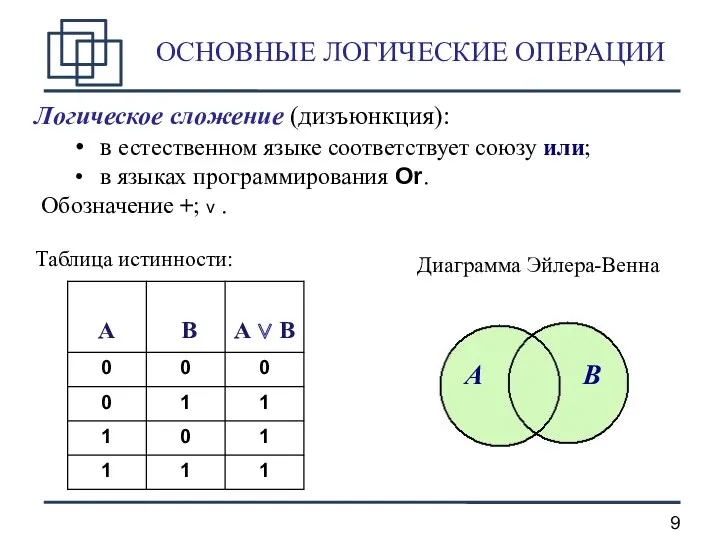
- 9. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое сложение (дизъюнкция): в естественном языке соответствует союзу или; в языках программирования Or.
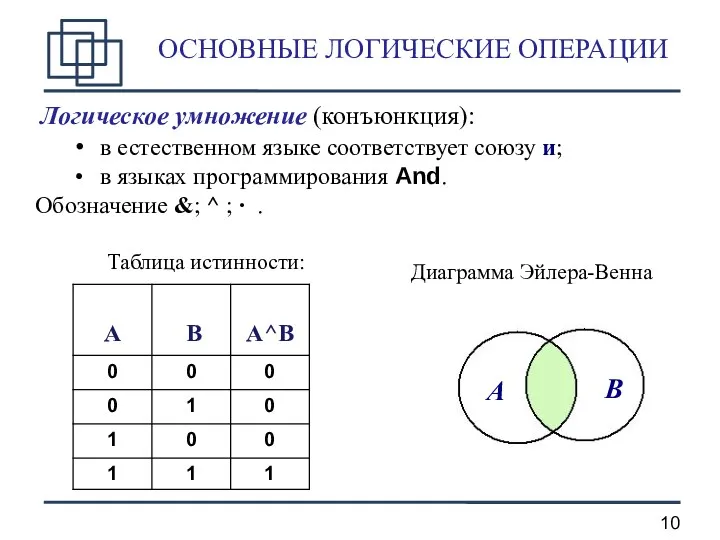
- 10. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое умножение (конъюнкция): в естественном языке соответствует союзу и; в языках программирования And.
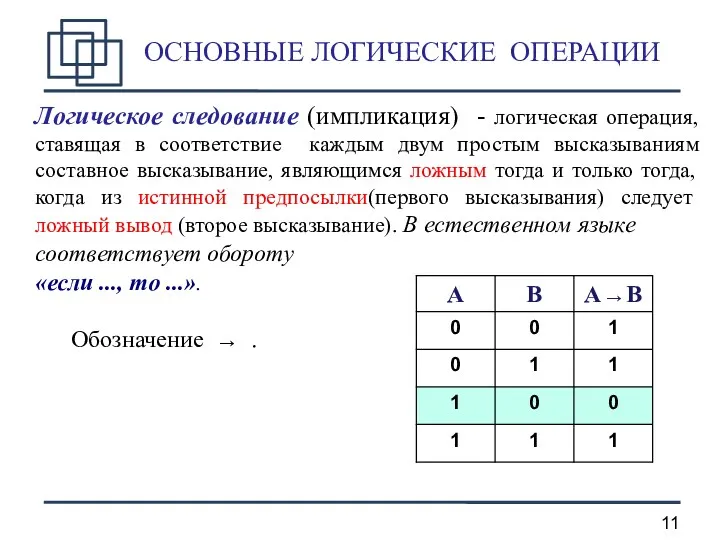
- 11. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое следование (импликация) - логическая операция, ставящая в соответствие каждым двум простым высказываниям
- 12. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическое следование соответствует высказыванию не A или B Сравним таблицы истинности: Логические выражения,
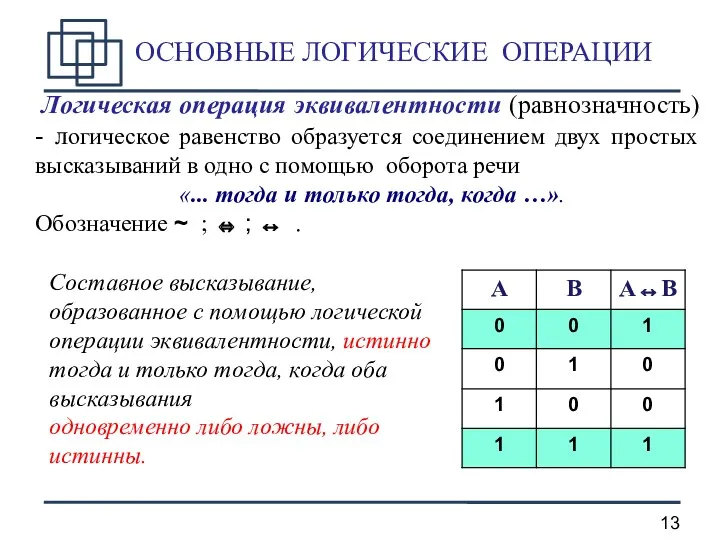
- 13. ОСНОВНЫЕ ЛОГИЧЕСКИЕ ОПЕРАЦИИ Логическая операция эквивалентности (равнозначность) - логическое равенство образуется соединением двух простых высказываний в
- 14. ПРИОРИТЕТ ВЫПОЛНЕНИЯ ЛОГИЧЕСКИХ ОПЕРАЦИЙ Логическое отрицание (инверсия) – «не»; ¬ ; ¯ . Логическое умножение (конъюнкция)
- 15. ТАБЛИЦЫ ИСТИННОСТИ Таблица истинности определяет истинность или ложность логической функции при всех возможных комбинациях исходных значений
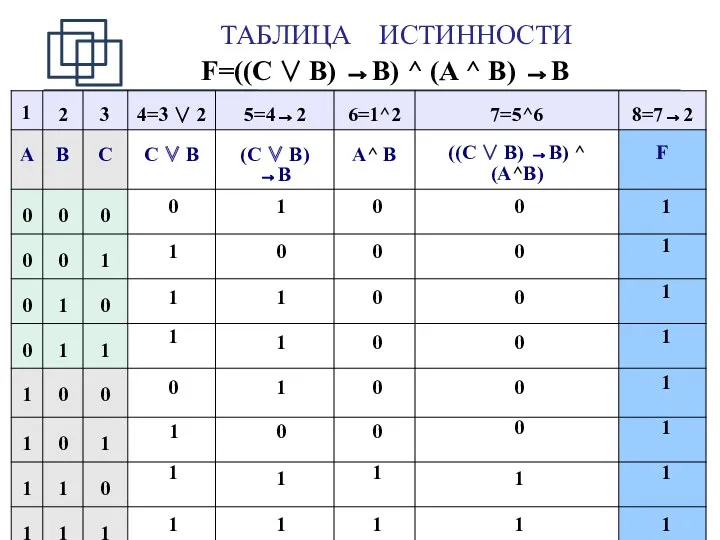
- 16. ТАБЛИЦЫ ИСТИННОСТИ Пример. Определить истинность формулы F=((C ∨ B) →B)^ (A^ B) →B Формула является тождественно
- 17. ТАБЛИЦА ИСТИННОСТИ F=((C ∨ B) →B) ^ (A ^ B) →B 0 1 1 1 0
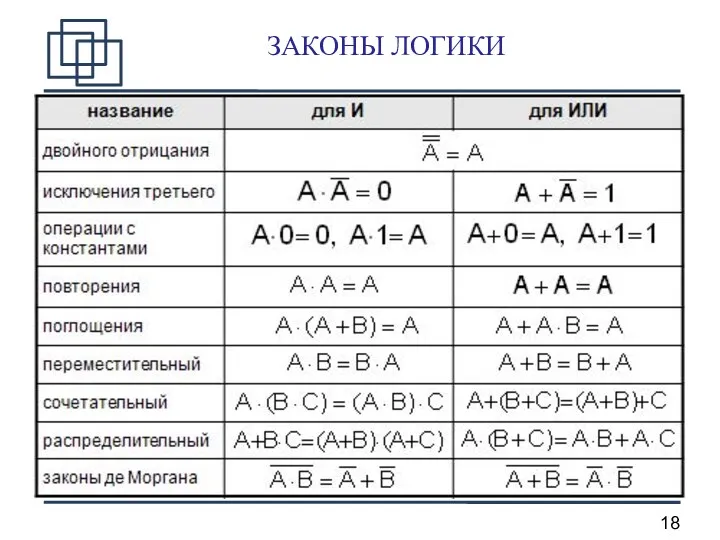
- 18. ЗАКОНЫ ЛОГИКИ
- 19. A7 (повышенный уровень, время – 3 мин) Для какого из указанных значений X истинно высказывание ¬((X
- 20. Определим порядок действий: сначала вычисляются результаты отношений в скобках, затем выполняется импликация (поскольку есть «большие» скобки),
- 21. 2) Выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); определяем
- 22. Возможные ловушки и проблемы Можно «забыть» отрицание (помните, что правильный ответ – всего один!) Можно перепутать
- 23. Решение (Вариант 2. Упрощение выражения) ¬((X > 2)→(X > 3)) Обозначим простые высказывания буквами: A =
- 24. Возможные проблемы Нужно помнить законы логики (например, формулы де Моргана). При использовании формул де Моргана нужно
- 25. Выводы В данном случае, наверное, проще первый вариант решения (прямая подстановка всех предложенных ответов). Второй вариант
- 26. A8 (базовый уровень, время – 1 мин) Укажите, какое логическое выражение равносильно выражению A ∧ ¬(¬B
- 27. Решение (Вариант 1. Использование законов де Моргана) Перепишем заданное выражение в других обозначениях: A ∧ ¬(¬B
- 28. Возможные ловушки и проблемы Серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений, поэтому
- 29. Решение (Вариант 2. Через таблицы истинности, если забыли формулы де Моргана) Перепишем заданное выражение в других
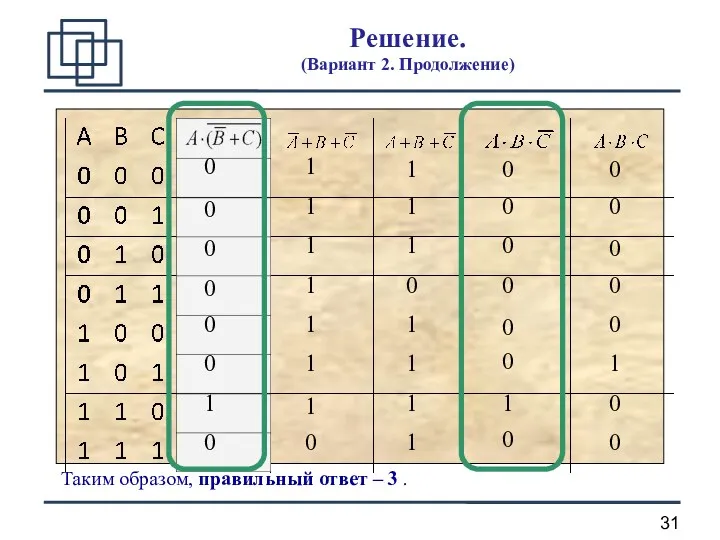
- 30. Решение (Вариант 2. Продолжение) Поэтому можно составить таблицы истинности для исходного выражения и всех ответов и
- 31. Решение. (Вариант 2. Продолжение) 1 0 0 0 0 0 0 0 0 1 1 1
- 32. Решение (комментарий к таблице) Исходное выражение истинно только тогда, когда и , то есть только при
- 33. Аналогично выражение ложно только при , а в остальных случаях – истинно. Решение (комментарий к таблице)
- 34. Возможные проблемы Выводы Сравнительно большой объем работы. Очевидно, что проще использовать первый вариант решения (упрощение исходного
- 35. Укажите значения переменных К, L, M, N, при которых логическое выражение (¬(М ∨ L) ∧ К)
- 36. Решение (вариант 1) Запишем уравнение (¬(М ∨ L) ∧ К) → (¬К ∧ ¬М) ∨ N)
- 37. Решение (вариант 1) Первое равенство выполняется тогда и только тогда, когда К=1 и . Отсюда следует
- 38. Переменные однозначно определяются только для ситуаций «сумма = 0» (все равны 0) и «произведение = 1»
- 39. Решение (вариант 2) Запишем уравнение (¬(М ∨ L) ∧ К) → (¬К ∧ ¬М) ∨ N)
- 40. Решение (вариант 2) Упростим выражение Тогда получим: Мы получили уравнение вида «сумма = 0», в нем
- 41. Этот способ работает всегда и дает более общее решение; в частности, можно легко обнаружить, что уравнение
- 42. Сколько различных решений имеет уравнение ((K ∨ L) → (L ∧ M ∧ N)) = 0
- 43. Решение Перепишем уравнение, используя более простые обозначения операций: ((K + L) → (L · M ·
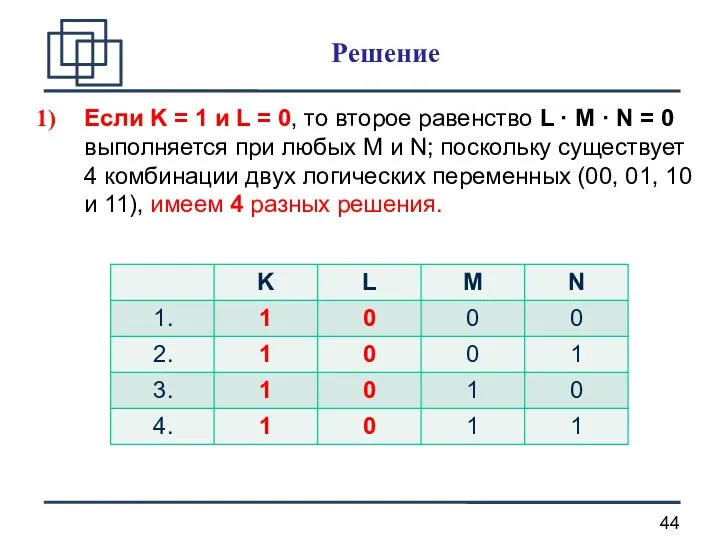
- 44. Если K = 1 и L = 0, то второе равенство L · M · N
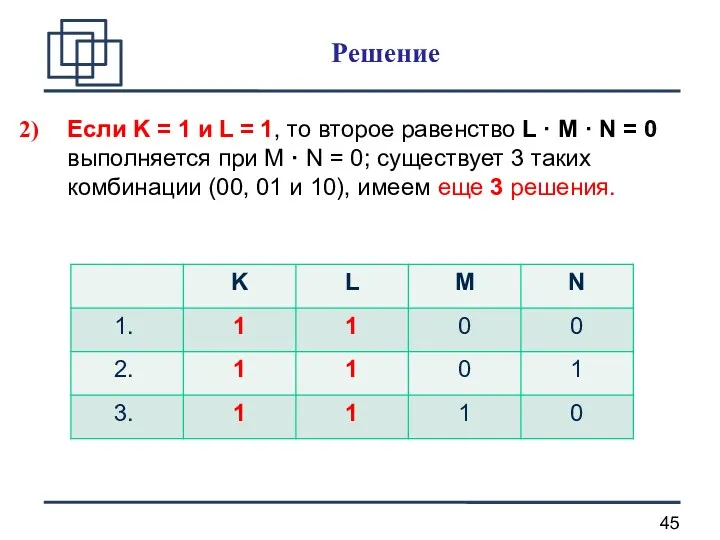
- 45. Если K = 1 и L = 1, то второе равенство L · M · N
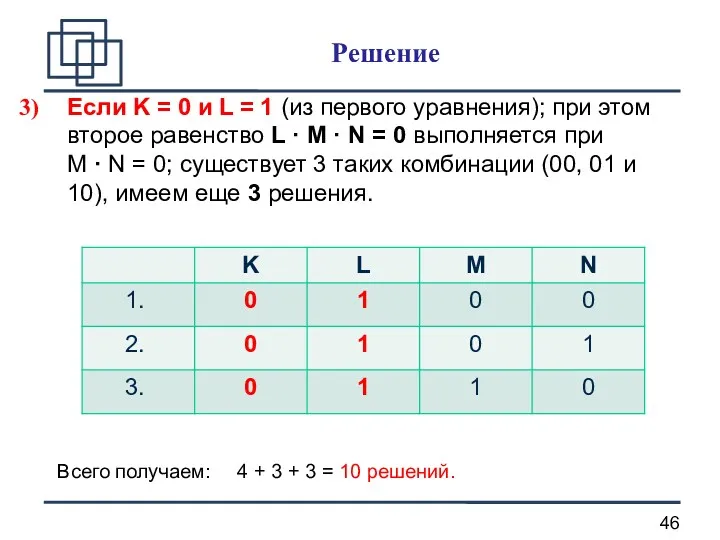
- 46. Если K = 0 и L = 1 (из первого уравнения); при этом второе равенство L
- 47. Совет Лучше начинать с того уравнения, где меньше переменных. Есть риск потерять какие-то решения при переборе
- 48. ЗАКОНЫ ЛОГИКИ Задание А7. Вариант 1 Логическое выражение ¬ Y ∨ ¬ ((X ∨ Y )
- 49. ЗАКОНЫ ЛОГИКИ Задание А7. Вариант 2 Логическое выражение ¬ (X ∨ Y ) ∨ ¬X ^
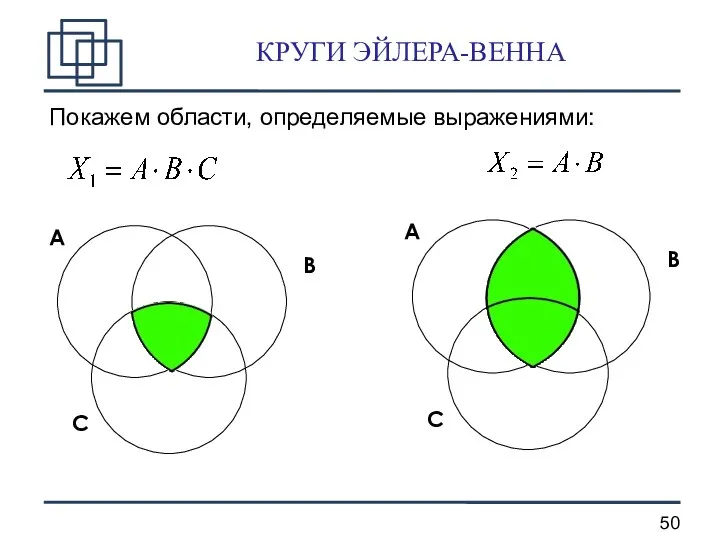
- 50. КРУГИ ЭЙЛЕРА-ВЕННА Покажем области, определяемые выражениями:
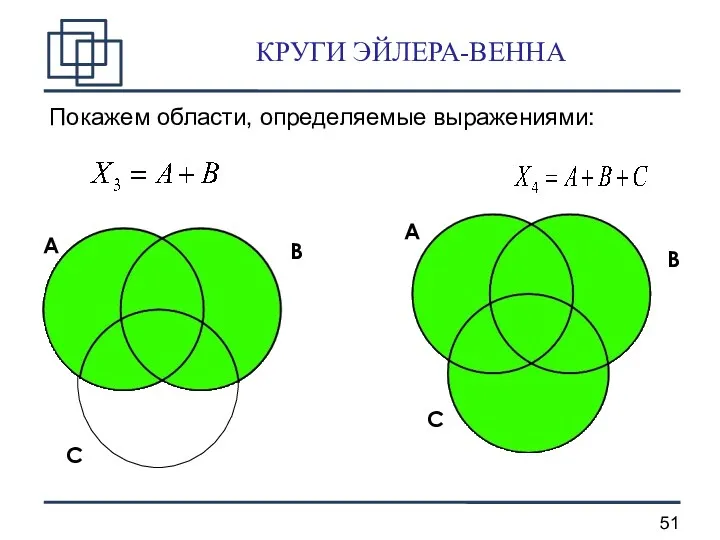
- 51. КРУГИ ЭЙЛЕРА-ВЕННА Покажем области, определяемые выражениями:
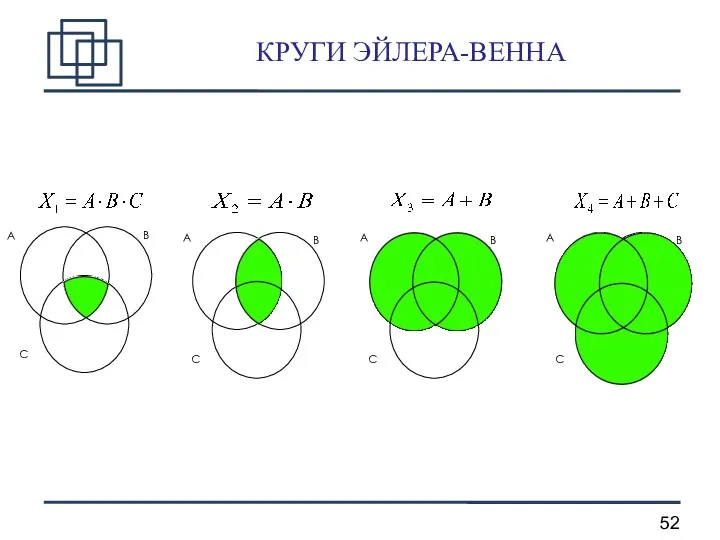
- 52. КРУГИ ЭЙЛЕРА-ВЕННА
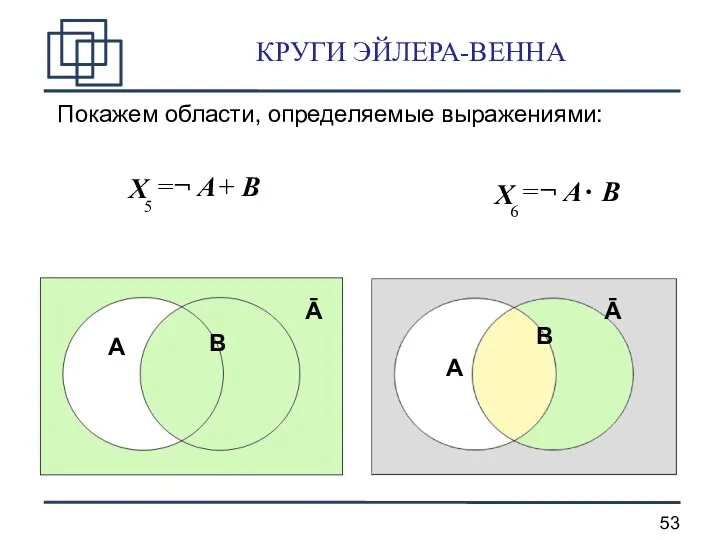
- 53. КРУГИ ЭЙЛЕРА-ВЕННА Покажем области, определяемые выражениями: A B Ā
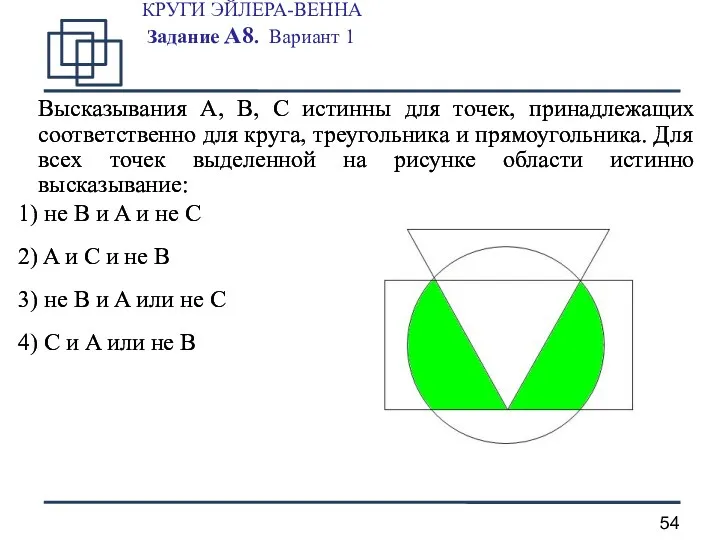
- 54. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 1 Высказывания A, B, C истинны для точек, принадлежащих соответственно для
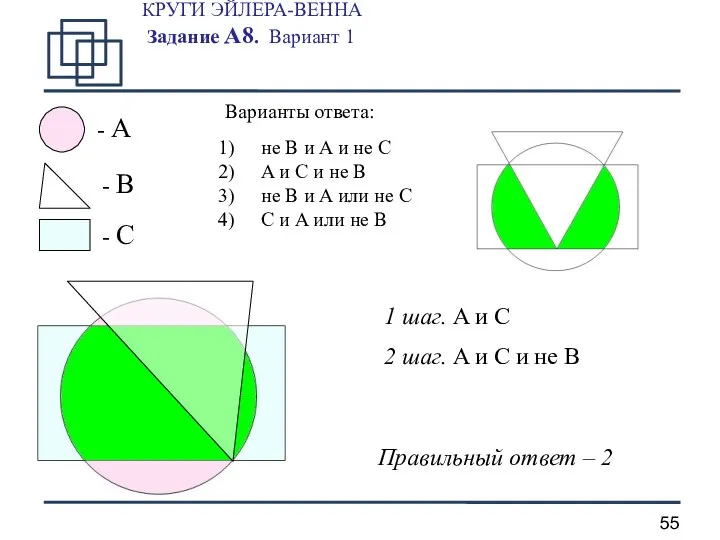
- 55. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 1 - A - B - C 1 шаг. A и
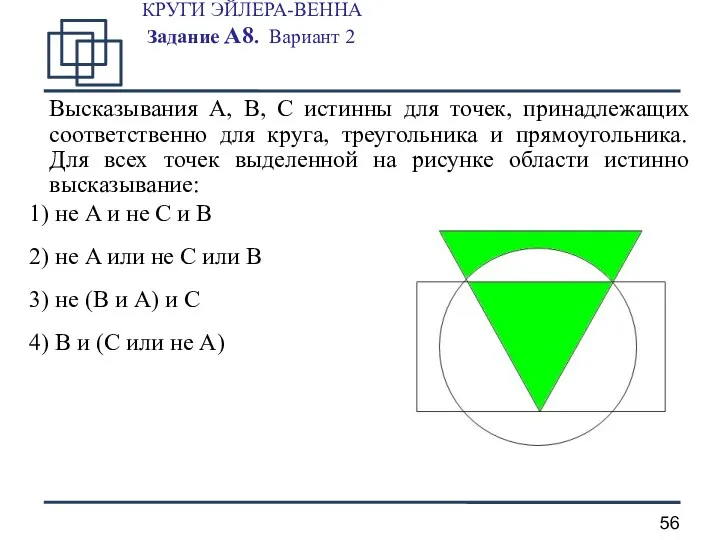
- 56. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 2 Высказывания A, B, C истинны для точек, принадлежащих соответственно для
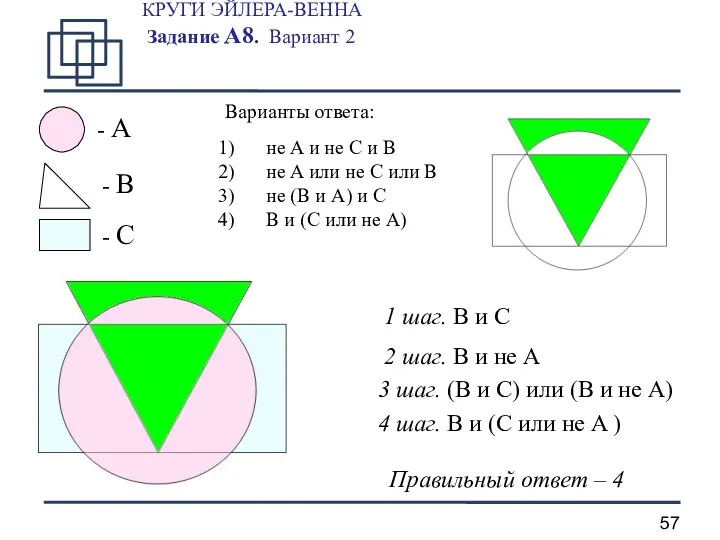
- 57. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 2 - A - B - C 1 шаг. B и
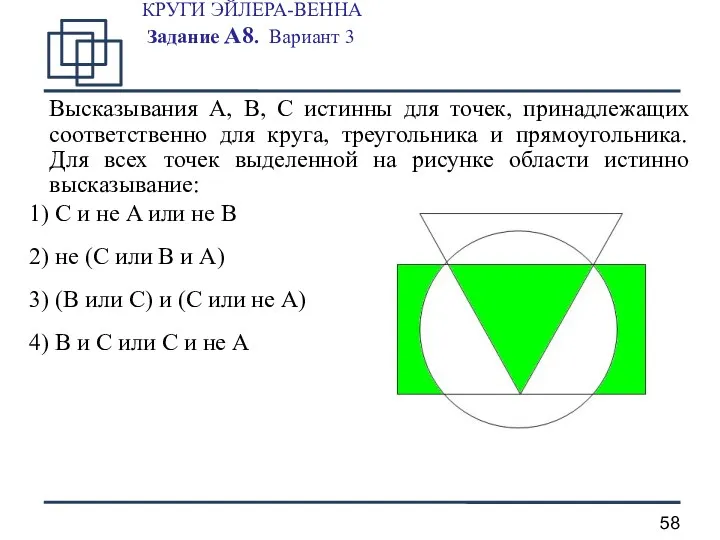
- 58. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 3 Высказывания A, B, C истинны для точек, принадлежащих соответственно для
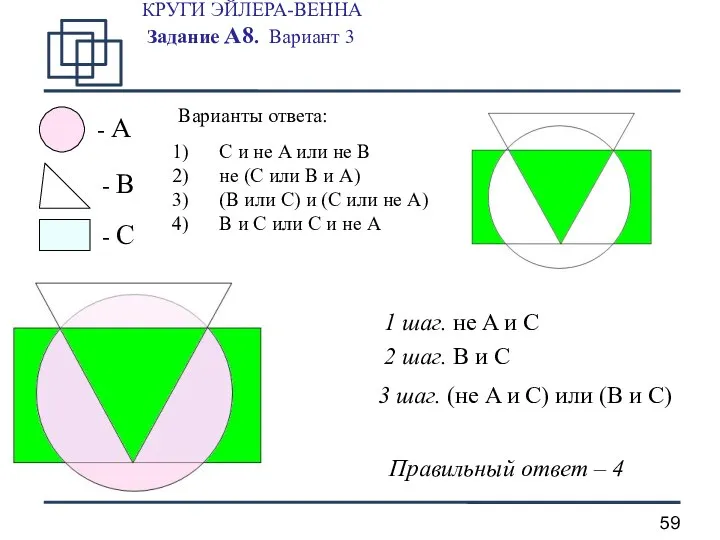
- 59. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 3 - A - B - C 1 шаг. не A
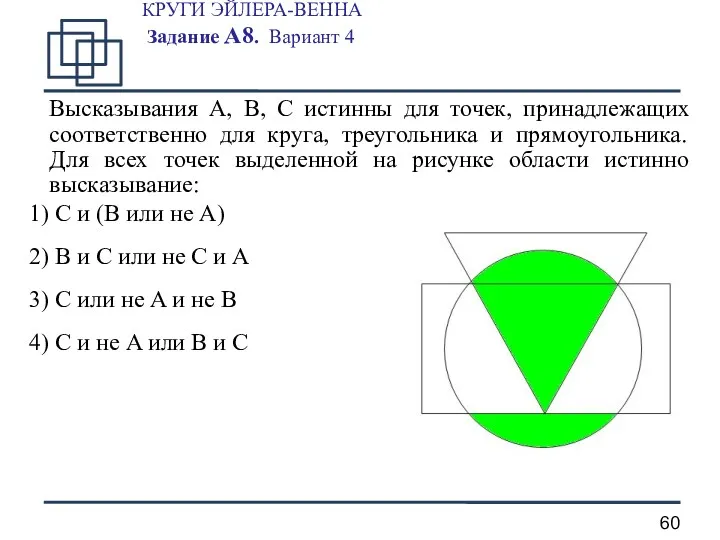
- 60. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 4 Высказывания A, B, C истинны для точек, принадлежащих соответственно для
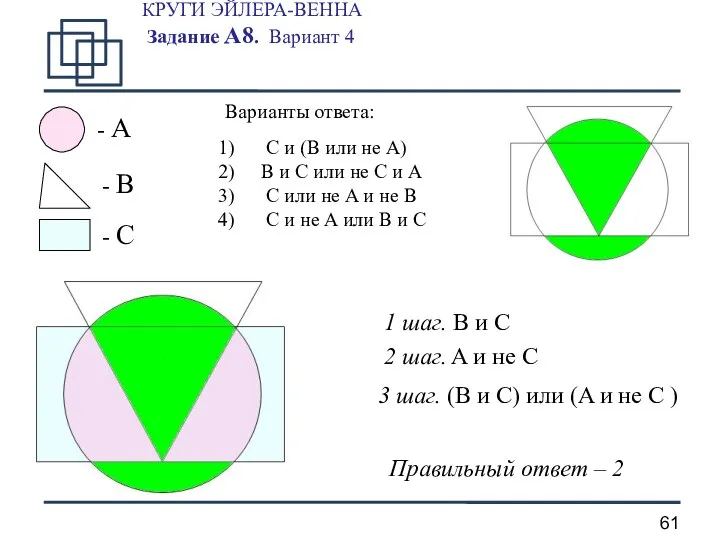
- 61. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 4 - A - B - C 1 шаг. B и
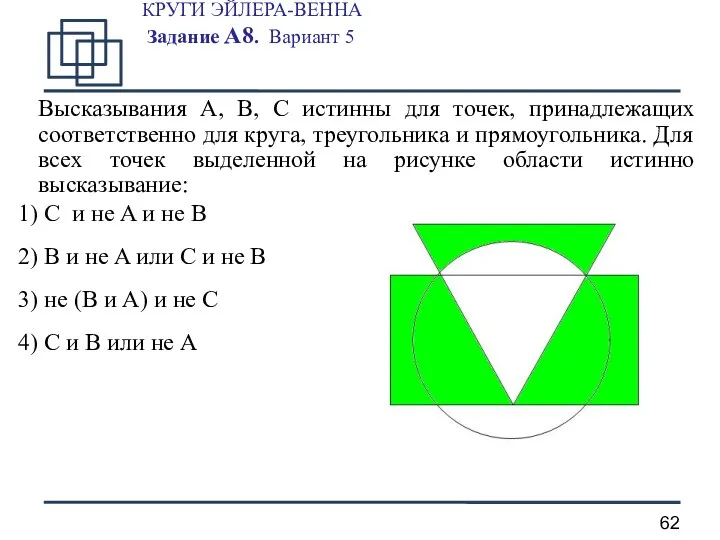
- 62. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 5 Высказывания A, B, C истинны для точек, принадлежащих соответственно для
- 63. КРУГИ ЭЙЛЕРА-ВЕННА Задание А8. Вариант 5 - A - B - C 1 шаг. C и
- 64. B10 (повышенный уровень, время – 5 мин) В таблице приведены запросы к поисковому серверу. Расположите номера
- 65. Решение (вариант 1) 1) принтеры & сканеры & продажа 2) принтеры & продажа 3) принтеры |
- 66. Возможные проблемы Нужно внимательно читать условие, так как в некоторых задачах требуется перечислить запросы в порядке
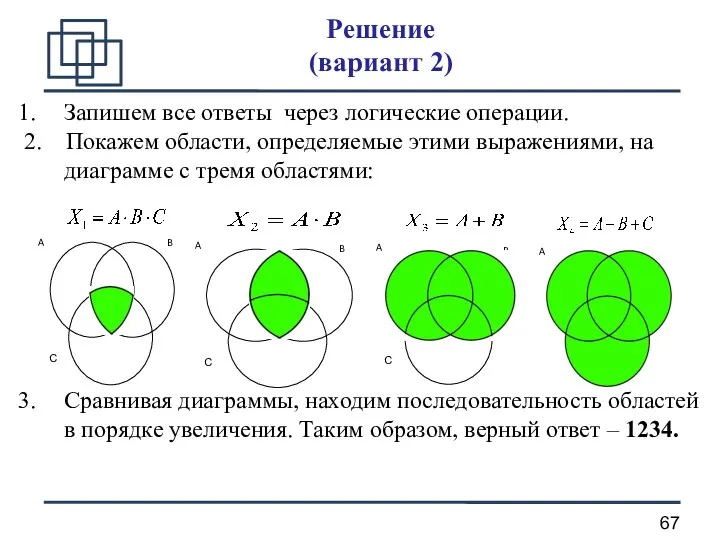
- 67. Решение (вариант 2) Запишем все ответы через логические операции. 2. Покажем области, определяемые этими выражениями, на
- 68. Получается громоздкий рисунок, если используется более трех переменных (более трех кругов). Возможные проблемы
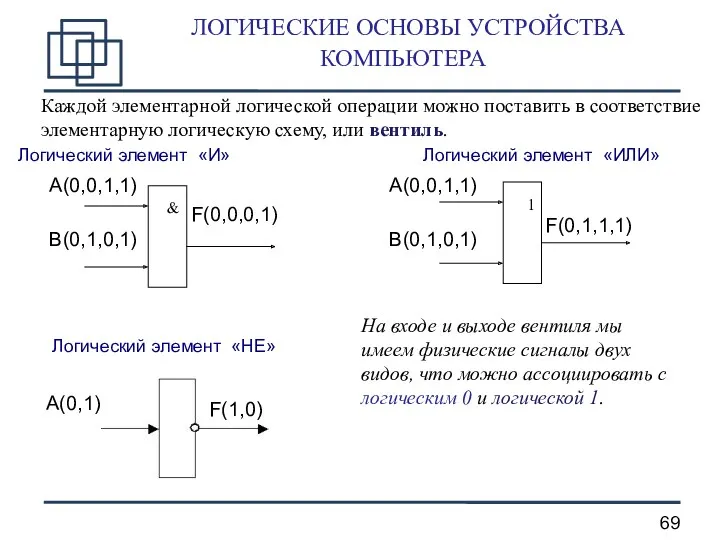
- 69. ЛОГИЧЕСКИЕ ОСНОВЫ УСТРОЙСТВА КОМПЬЮТЕРА А(0,0,1,1) B(0,1,0,1) F(0,0,0,1) Логический элемент «И» Логический элемент «ИЛИ» А(0,0,1,1) B(0,1,0,1) F(0,1,1,1)
- 70. ЛОГИЧЕСКИЕ СХЕМЫ Построение логических схем по булеву выражению. Определить число переменных. Определить количество логических операций и
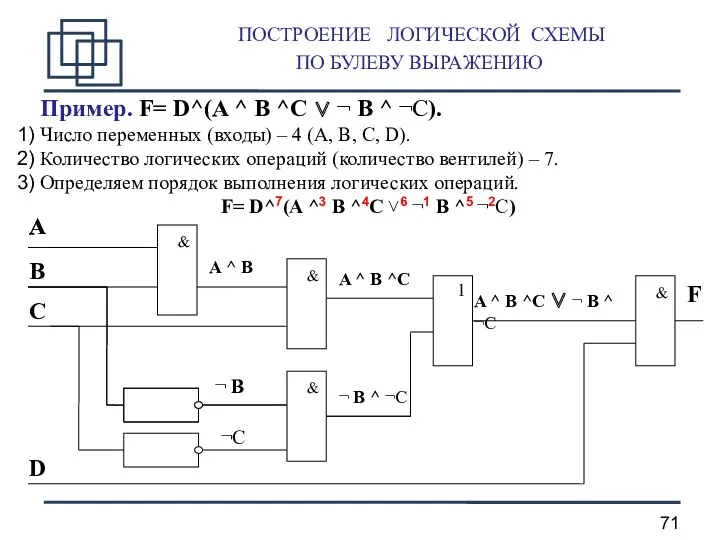
- 71. ПОСТРОЕНИЕ ЛОГИЧЕСКОЙ СХЕМЫ ПО БУЛЕВУ ВЫРАЖЕНИЮ Пример. F= D^(A ^ B ^C ∨ ¬ B ^
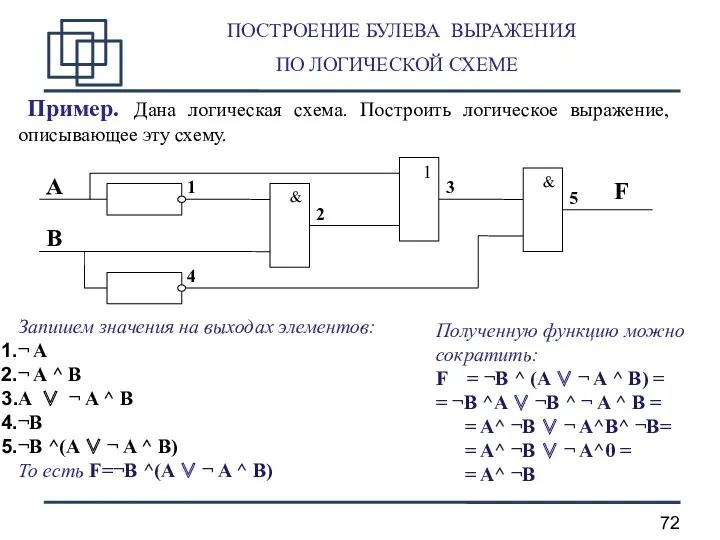
- 72. ПОСТРОЕНИЕ БУЛЕВА ВЫРАЖЕНИЯ ПО ЛОГИЧЕСКОЙ СХЕМЕ Пример. Дана логическая схема. Построить логическое выражение, описывающее эту схему.
- 73. ПОСТРОЕНИЕ БУЛЕВА ВЫРАЖЕНИЯ ПО ТАБЛИЦЕ ИСТИННОСТИ Для каждой строки таблицы с единичным значением функции построить минтерм.
- 74. ПОСТРОЕНИЕ БУЛЕВА ВЫРАЖЕНИЯ ПО ТАБЛИЦЕ ИСТИННОСТИ Пример. Дана таблица истинности. Построим булево выражение для F. Найдем
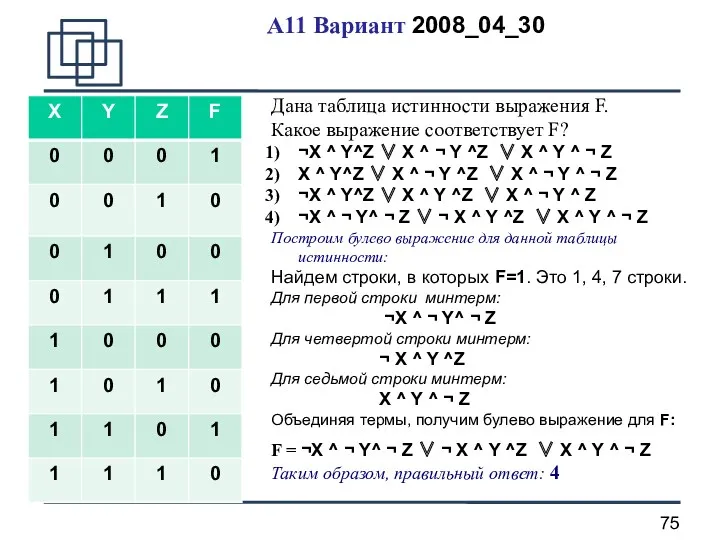
- 75. A11 Вариант 2008_04_30 Дана таблица истинности выражения F. Какое выражение соответствует F? ¬X ^ Y^Z ∨
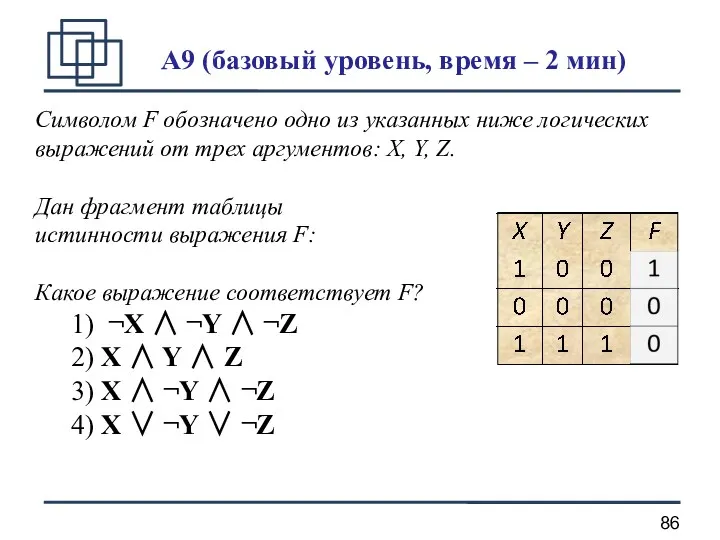
- 76. A9 (базовый уровень, время – 2 мин) Символом F обозначено одно из указанных ниже логических выражений
- 77. Решение (Основной вариант) Нужно для каждой строчки подставить заданные значения X, Y и Z во все
- 78. Решение (Основной вариант) Перепишем ответы в других обозначениях: ¬X ∧ ¬Y ∧ ¬Z = X ∧
- 79. Первое выражение, , равно 1 только при , поэтому это неверный ответ (первая строка таблицы не
- 80. Второе выражение, , равно 1 только при , поэтому это неверный ответ (первая и вторая строки
- 81. Третье выражение, , равно нулю при , поэтому это неверный ответ (третья строка таблицы не подходит)
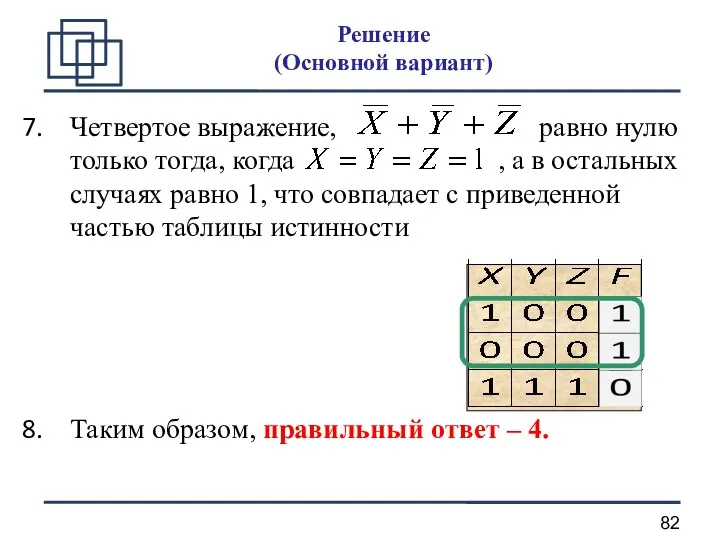
- 82. Четвертое выражение, равно нулю только тогда, когда , а в остальных случаях равно 1, что совпадает
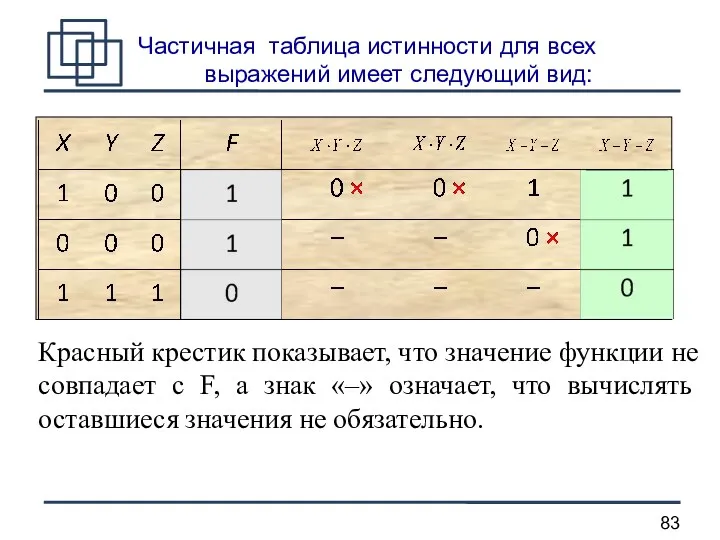
- 83. Частичная таблица истинности для всех выражений имеет следующий вид: Красный крестик показывает, что значение функции не
- 84. Возможные ловушки и проблемы Серьезные сложности представляет применяемая в заданиях ЕГЭ форма записи логических выражений, поэтому
- 85. Решение (вариант 2) Часто правильный ответ – это самая простая функция, удовлетворяющая частичной таблице истинности, то
- 86. A9 (базовый уровень, время – 2 мин) Символом F обозначено одно из указанных ниже логических выражений
- 87. Решение Перепишем ответы в других обозначениях: ¬X ∧ ¬Y ∧ ¬Z = X ∧ Y ∧
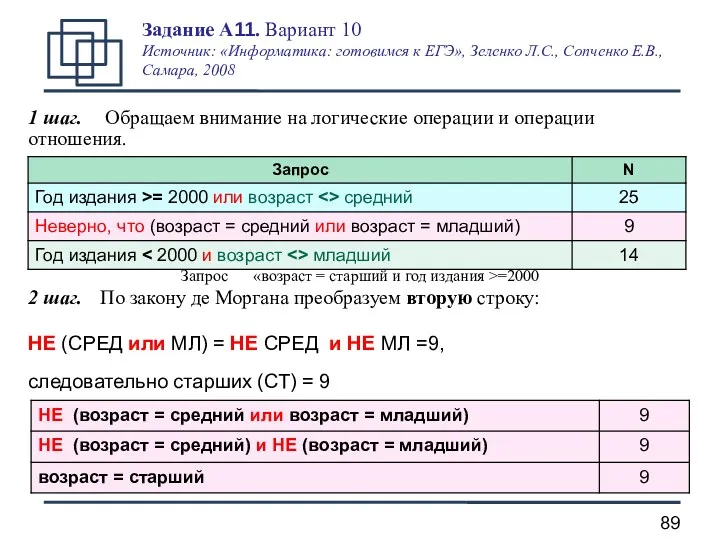
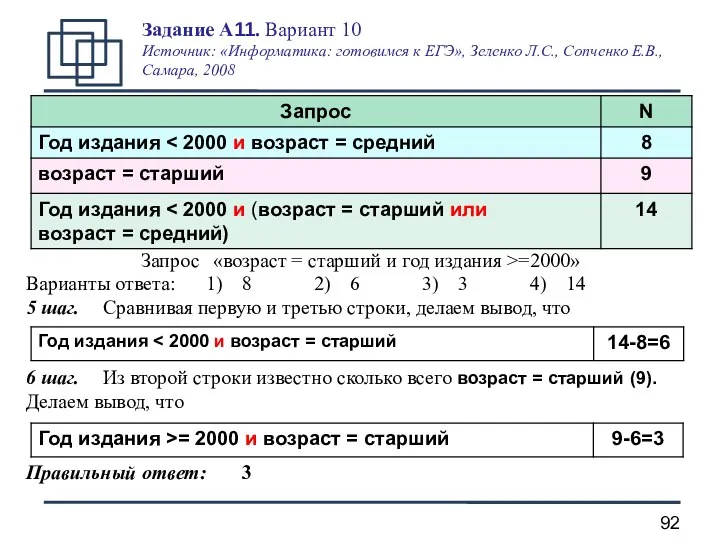
- 88. Задание А11. Вариант 10 Источник: «Информатика: готовимся к ЕГЭ», Зеленко Л.С., Сопченко Е.В., Самара, 2008 База
- 89. 1 шаг. Обращаем внимание на логические операции и операции отношения. Запрос «возраст = старший и год
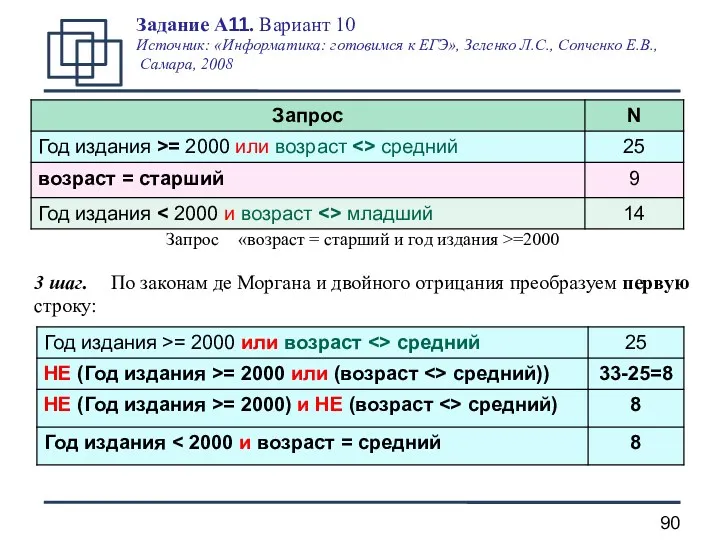
- 90. Запрос «возраст = старший и год издания >=2000 3 шаг. По законам де Моргана и двойного
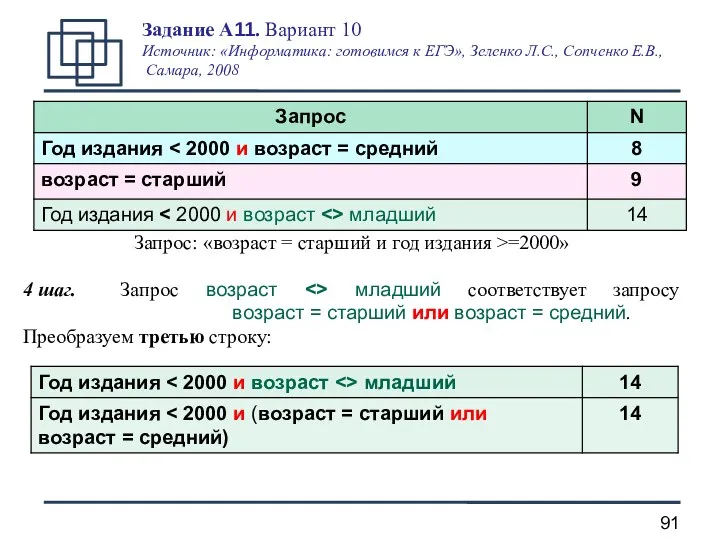
- 91. Запрос: «возраст = старший и год издания >=2000» 4 шаг. Запрос возраст младший соответствует запросу возраст
- 92. Запрос «возраст = старший и год издания >=2000» Варианты ответа: 1) 8 2) 6 3) 3
- 93. Алгоритм решения логических задач внимательно изучить условие; выделить простые высказывания и обозначить их латинскими буквами; записать
- 94. В школьном первенстве по настольному теннису в четверку лучших вошли девушки: Наташа, Маша, Люда и Рита.
- 95. Наташа – 1 Маша – 4 Люда – 2 Рита – 3 ⇒ ⇒ Ответ: 1423
- 96. Перед началом Турнира Четырех болельщики высказали следующие предположения по поводу своих кумиров: А) Макс победит, Билл
- 97. Решение Применим к этой задаче формальный аппарат математической логики. Каждый из трех болельщиков высказал два утверждения,
- 98. Решение (М1 · ¬ Б2 + ¬ М1 · Б2) · (Б3 · ¬Н1+ ¬ Б3
- 99. Классный руководитель пожаловался директору, что у него в классе появилась компания из 3-х учеников, один из
- 100. Решение (вариант 1) Во-первых, есть «точная» информация, которая не подвергается сомнению: (*) все трое прогуляли урок
- 101. Решение (вариант 1) Коля: 1. Я всегда прогуливаю астрономию. 2. Саша врет. Саша: 1. Я в
- 102. Решение (вариант 1) Коля: лжет Саша: 1. Я в первый раз прогулял астрономию. Миша:1. Коля говорит
- 103. Возможные проблемы Длинное запутанное условие, из которого нужно выделить действительно существенную информацию и формализовать ее. Легко
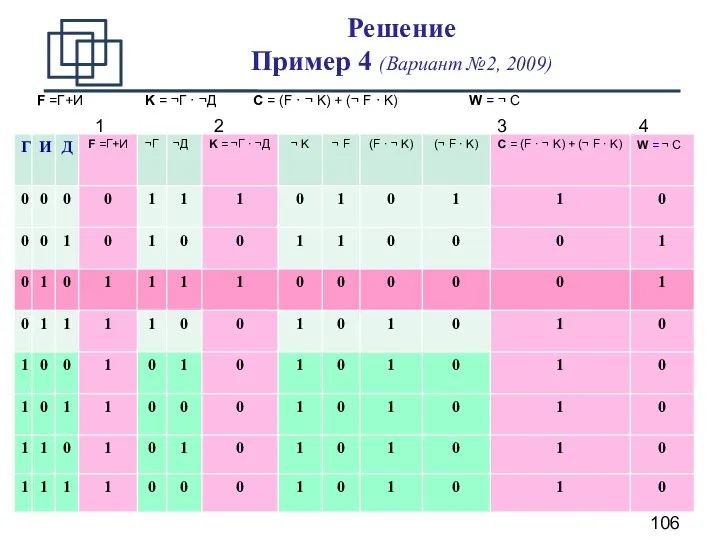
- 104. B6 (повышенный уровень, время – 8 мин) Пример 4 (Вариант №2, 2009) Один из пяти братьев
- 105. Решение Пример 4 (Вариант №2, 2009) Обозначим высказывания: F =Г+И Никита: «Пирог испек Глеб или Игорь».
- 106. Решение Пример 4 (Вариант №2, 2009) F =Г+И K = ¬Г · ¬Д C = (F
- 107. B6 (повышенный уровень, время – 8 мин) Пример 5 (Вариант №1, 2009) Три друга – Петр,
- 108. Решение Пример 5 (Вариант №1, 2009) A Петр - математик B Сергей-не физик C Роман физик
- 109. Три студента Антонов, Волков, Сергеев стремятся сдать сессию на отлично. Были высказаны следующие предположения: сдача экзаменов
- 110. Андрей, Ваня и Саша собрались в поход. Учитель хорошо знавший этих ребят, высказал следующие предположения: Андрей
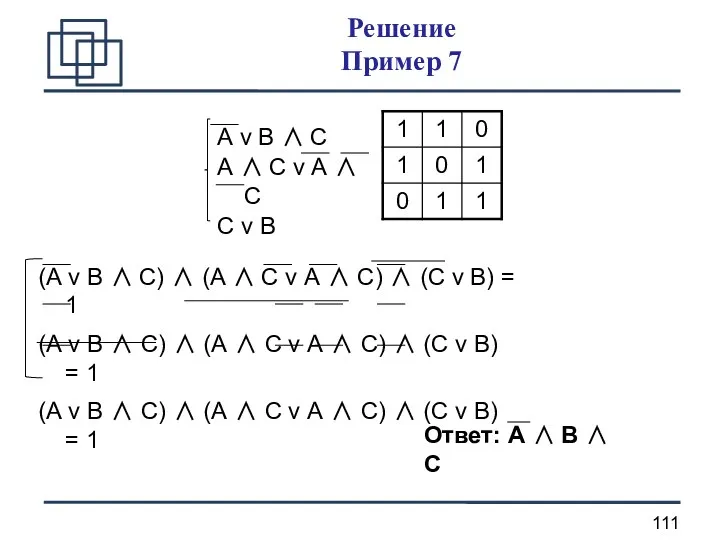
- 111. Решение Пример 7
- 113. Скачать презентацию







































































 Кіберзлочинність
Кіберзлочинність Качество программного обеспечения
Качество программного обеспечения Основные компоненты Microsoft Outlook
Основные компоненты Microsoft Outlook Веб-страницы и веб-сайты (самый крупный) до (самый мелкий).Некоторые тэги имеют атрибуты, которые являются именами свойств и принимают определенные значения.ALIGN =“ center” – тип выравнивания заголовкаС помощью тега FONT можно зад
Веб-страницы и веб-сайты (самый крупный) до (самый мелкий).Некоторые тэги имеют атрибуты, которые являются именами свойств и принимают определенные значения.ALIGN =“ center” – тип выравнивания заголовкаС помощью тега FONT можно зад Sportarena. Сайт спортивных новостей
Sportarena. Сайт спортивных новостей Автоматизированный способ контроля доступа сотрудников к рабочим местам
Автоматизированный способ контроля доступа сотрудников к рабочим местам Енгізіү және тарату құрылғылары
Енгізіү және тарату құрылғылары Интеллектуальная игра Хакеры
Интеллектуальная игра Хакеры Алгоритмизация и программирование. Лекция 1
Алгоритмизация и программирование. Лекция 1 Символьные строки
Символьные строки Поняття моделі. Типи моделей
Поняття моделі. Типи моделей Программирование на алгоритмическом языке
Программирование на алгоритмическом языке Инженерия знаний. Лекция 1
Инженерия знаний. Лекция 1 Экспертные системы
Экспертные системы Вычисление количества информации. Решение задач
Вычисление количества информации. Решение задач Процессор. Процесс обработки данных и управление этим процессом
Процессор. Процесс обработки данных и управление этим процессом Разработка детской настольной игры
Разработка детской настольной игры Технології створення лонгридів
Технології створення лонгридів Серверные операционные системы
Серверные операционные системы Инструкция по регистрации в мобильном приложении НПФ Будущее
Инструкция по регистрации в мобильном приложении НПФ Будущее Самозванец. Игра
Самозванец. Игра Microsoft official course. Creating methods, handling exceptions, and monitoring applications. (Module 2)
Microsoft official course. Creating methods, handling exceptions, and monitoring applications. (Module 2) Обработка информации
Обработка информации Java Generics. Лекция 4
Java Generics. Лекция 4 Интернет. Интернеттің шығу тарихы
Интернет. Интернеттің шығу тарихы Тезаурус Безопасный интернет
Тезаурус Безопасный интернет История возникновения чисел
История возникновения чисел История счета и систем счисления
История счета и систем счисления