Содержание
- 2. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Задача согласования дискретного источника с дискретным каналом с шумом X – ансамбль сигналов
- 3. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Теорема Шеннона для дискретного канала с шумом Если производительность источника сообщений H'(U) меньше
- 4. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Алгебраическое основы операций кодирования и декодирования Функции кодирования и декодирования включают арифметические операции
- 5. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Методика построения помехоустойчивых кодов. Модели ошибок В каждом разряде вектора ошибки единица появляется
- 6. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Методика построения помехоустойчивых кодов. Характеристики кодов Коэффициент повышения верности Kпв при использовании помехоустойчивого
- 7. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Методика построения помехоустойчивых кодов. Характеристики кодов Избыточные блочные коды (длины n = k+r):
- 8. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Методика построения помехоустойчивых кодов. Характеристики кодов Для обнаружения всех ошибок кратности, не превышающей
- 9. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Методика построения помехоустойчивых кодов. Оптимальные помехоустойчивые коды Верхняя граница кодового расстояния dmin при
- 10. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Линейные блочные коды. Порождающая и проверочная матрицы Пусть x1, x2, ..., xk означают
- 11. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Линейные блочные коды. Порождающая и проверочная матрицы Систематическая (каноническая) форма порождающей матрицы G
- 12. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Линейные блочные коды. Синдром ошибки Проверочная матрица Hn,k имеет rxn элементов, причем справедливо:
- 13. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Линейные блочные коды. Порождающая и проверочная матрицы Отрицательный знак можно опустить, поскольку при
- 14. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Код Хэмминга (для dmin=3) Число информационных разрядов k и размер кодового слова n
- 15. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Код Хэмминга. Проверочная и порождающая матрицы Особенность проверочной матрицы кода Хэмминга: для двоичного
- 16. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Расширенный код Хэмминга Кодовые вектора дополняются двоичным разрядом так, чтобы число единиц, содержащихся
- 17. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Расширенный код Хэмминга Проверочная матрица H (2w,k)-кода получается из проверочной матрицы (2w-1,k)-кода: -
- 18. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Циклические коды Циклические коды являются подмножеством линейных кодов и обладают свойствами, упрощающими процессы
- 19. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Циклические коды Кодовое слово v, состоящее из n битов, определяется полиномом v(X) =
- 20. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Циклические коды. Порождающий многочлен Порождающий многочлен – неприводимый ненулевой многочлен (или произведение неприводимых
- 21. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Циклические коды. Проверочный многочлен Проверочный многочлен циклического кода является множителем (xn+1), т.е. h(X)
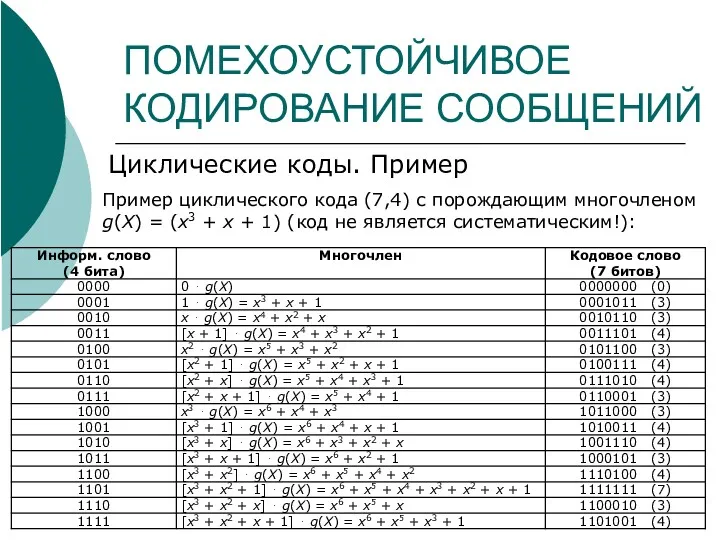
- 22. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Циклические коды. Пример Пример циклического кода (7,4) с порождающим многочленом g(X) = (x3
- 23. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Циклические коды. Порождающая матрица Каждое кодовое слово может быть представлен в виде произведения
- 24. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Циклические коды. Проверочная матрица Для получения проверочной матрицы используется утверждение, что порождающий многочлен
- 25. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Систематические циклические коды. Рассмотрим информационный многочлен степени k-1: a(X) = ak-1xk-1 + ...
- 26. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Деление многочленов с использованием регистра сдвига При кодировании систематическим кодом операция деления выполняется
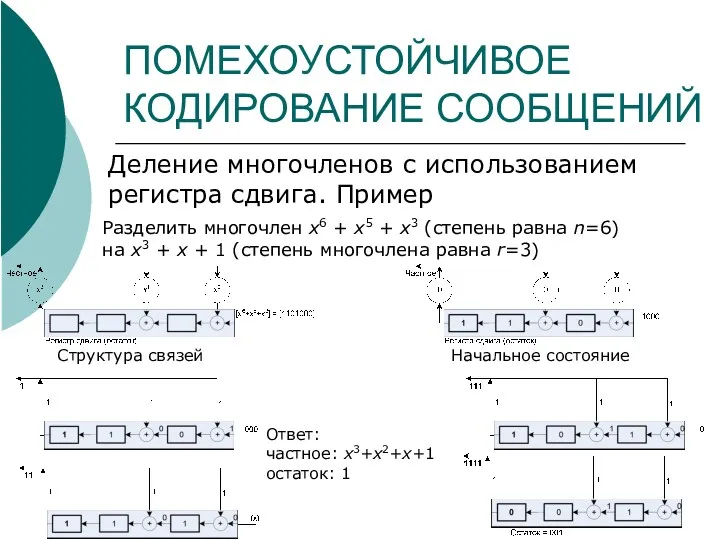
- 27. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Деление многочленов с использованием регистра сдвига. Пример Разделить многочлен x6 + x5 +
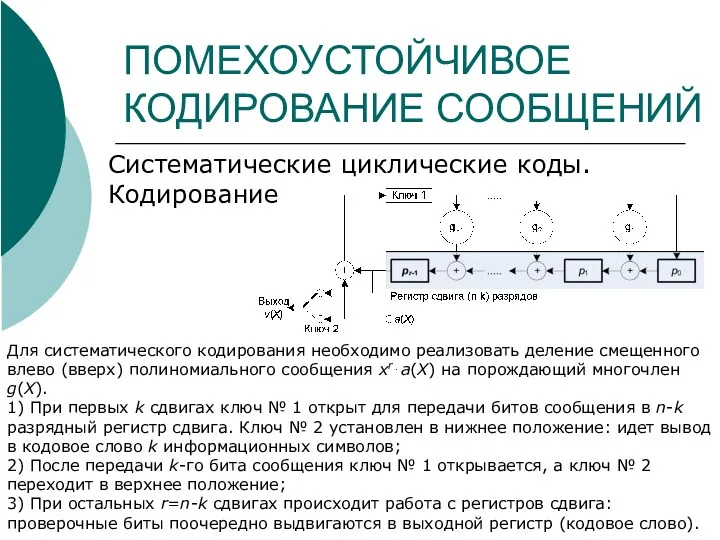
- 28. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Систематические циклические коды. Кодирование Для систематического кодирования необходимо реализовать деление смещенного влево (вверх)
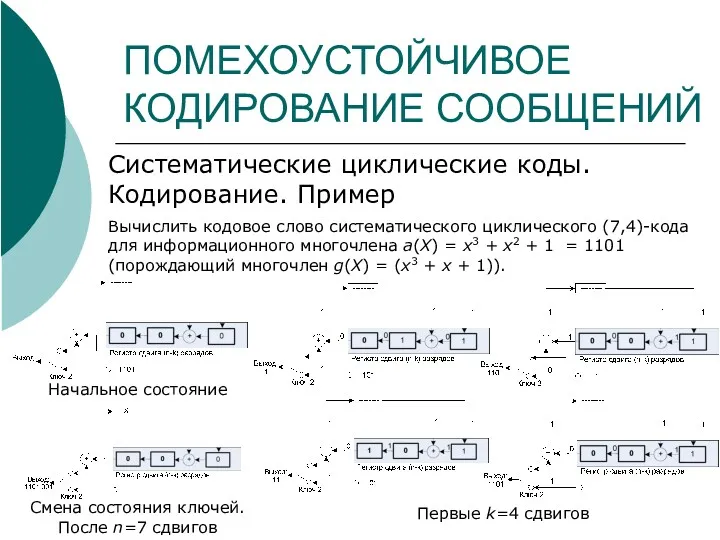
- 29. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Систематические циклические коды. Кодирование. Пример Вычислить кодовое слово систематического циклического (7,4)-кода для информационного
- 30. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Систематические циклические коды. Декодирование. Синдром ошибки При передачи данных по каналу связи с
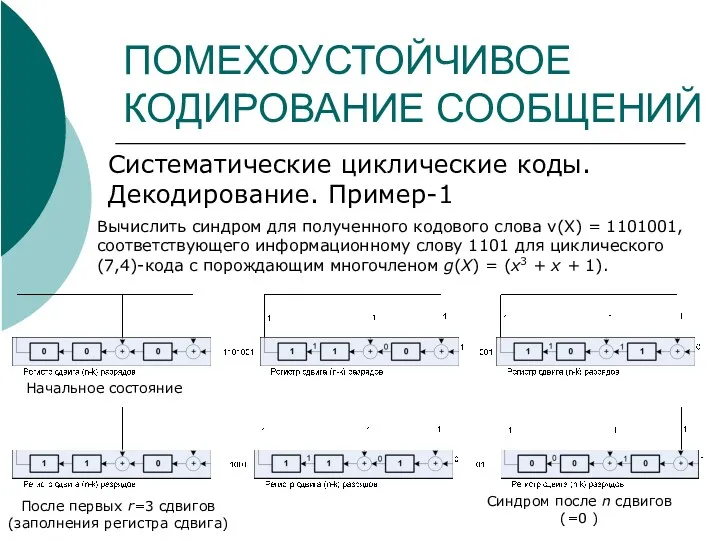
- 31. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Систематические циклические коды. Декодирование. Пример-1 Вычислить синдром для полученного кодового слова v(X) =
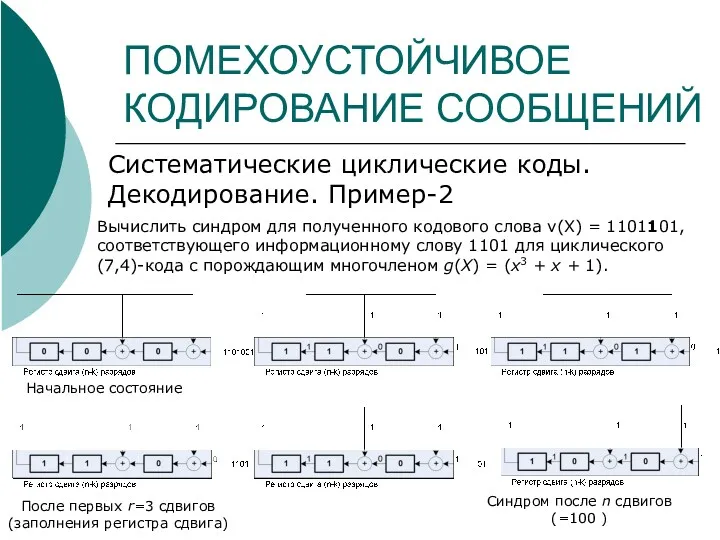
- 32. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Систематические циклические коды. Декодирование. Пример-2 Вычислить синдром для полученного кодового слова v(X) =
- 33. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Систематические циклические коды. Декодирование. Исправление ошибки Возьмем в качестве отправной точки синдром ошибки
- 34. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Дополнительные возможности циклических кодов Особенность циклических кодов - способность к распознаванию пакетов ошибок
- 35. ПОМЕХОУСТОЙЧИВОЕ КОДИРОВАНИЕ СООБЩЕНИЙ Выполнение лабораторной работы № 3. Вариант моделирования шума в канале связи Для генерации
- 37. Скачать презентацию




























 Строки
Строки Как составить презентацию по бизнес-проекту
Как составить презентацию по бизнес-проекту Розподілені системи обробки інформації
Розподілені системи обробки інформації Microsoft Excel кестелік процессорында жұмыс істеу. Электрондық кестелерді әзірлеу
Microsoft Excel кестелік процессорында жұмыс істеу. Электрондық кестелерді әзірлеу Review or research in software defect reporting
Review or research in software defect reporting Создание автоматизированного рабочего места для технического секретаря приемной комиссии ГБПОУ КК БАК Брюховецкого района
Создание автоматизированного рабочего места для технического секретаря приемной комиссии ГБПОУ КК БАК Брюховецкого района Веб-интерфейс информационной системы обеспечения деятельности ООО Русский лес
Веб-интерфейс информационной системы обеспечения деятельности ООО Русский лес Автоматизированные банковские системы
Автоматизированные банковские системы Абсолютная, относительная и смешанная ссылки
Абсолютная, относительная и смешанная ссылки Свойства алгоритма и его исполнители
Свойства алгоритма и его исполнители API Вконтакте - пример использования
API Вконтакте - пример использования Выделение и описание бизнес-процессов в организации
Выделение и описание бизнес-процессов в организации Информатика и ИКТ 10-11 класс. Системы счисления
Информатика и ИКТ 10-11 класс. Системы счисления Инструкция по работе в Системе САКД
Инструкция по работе в Системе САКД Проект Профстажировки 2.0. Формирование и работа с кейсами партнеров проекта
Проект Профстажировки 2.0. Формирование и работа с кейсами партнеров проекта Маршрутизаторы, функция VPN
Маршрутизаторы, функция VPN Welcome To ZyXEL Router Customer Care Center. How to Install a ZyXEL Router
Welcome To ZyXEL Router Customer Care Center. How to Install a ZyXEL Router Измерение информации. Меры информации
Измерение информации. Меры информации Функциональные возможности Microsoft Office
Функциональные возможности Microsoft Office Настройка сетевой операционной системы
Настройка сетевой операционной системы Презентация к уроку информатики на тему: Правила поведения в компьютерном классе.
Презентация к уроку информатики на тему: Правила поведения в компьютерном классе.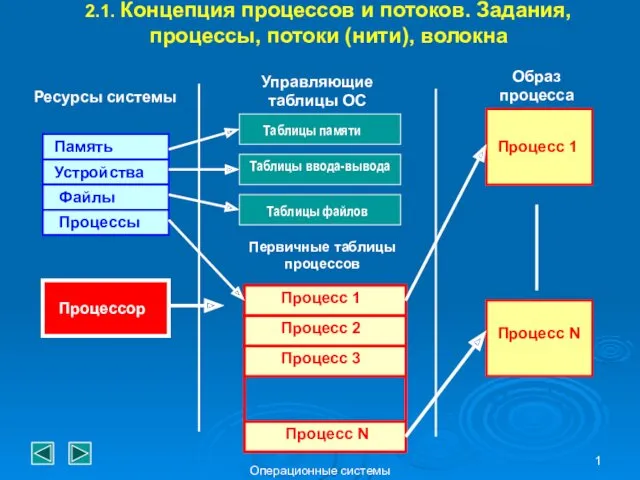 Концепция процессов и потоков. Задания, процессы, потоки, волокна
Концепция процессов и потоков. Задания, процессы, потоки, волокна Програмна оболонка Norton Commander
Програмна оболонка Norton Commander Методическая подготовка и сопровождение педагогов сельской школы
Методическая подготовка и сопровождение педагогов сельской школы Двумерные массивы
Двумерные массивы Глобальные и локальные компьютерные сети
Глобальные и локальные компьютерные сети Введение в информатику - Сказка о друзьях или о том, как появился компьютер
Введение в информатику - Сказка о друзьях или о том, как появился компьютер Архитектура ПК
Архитектура ПК