Содержание
- 2. Propositions Our discussion begins with an introduction to the basic building blocks of logic – propositions.
- 3. Propositions Example 1 All the following declarative sentences are propositions. 1. Minsk is the capital of
- 4. Propositions
- 5. Propositions
- 6. Propositions The area of logic that deals with propositions is called the propositional calculus or propositional
- 7. Compound propositions We now turn our attention to methods for producing new propositions from those that
- 8. Compound propositions Many mathematical statements are constructed by combining one or more propositions. New propositions, called
- 9. The negation of a proposition
- 10. The negation of a proposition
- 11. The negation of a proposition Example 3 Find the negation of the proposition “Vandana’s smartphone has
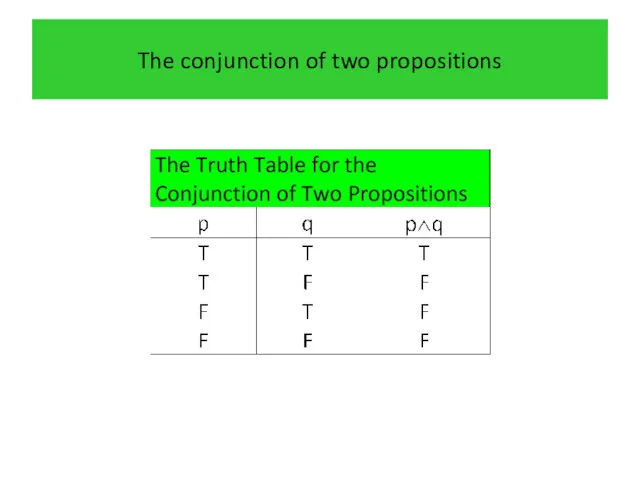
- 12. The conjunction of two propositions Definition 3 Let p and q be propositions. The conjunction of
- 13. The conjunction of two propositions
- 14. The conjunction of two propositions Example 4 Find the conjunction of the propositions p and q
- 15. The conjunction of two propositions Solution The conjunction of these propositions, p∧q, is the proposition “Rebecca’s
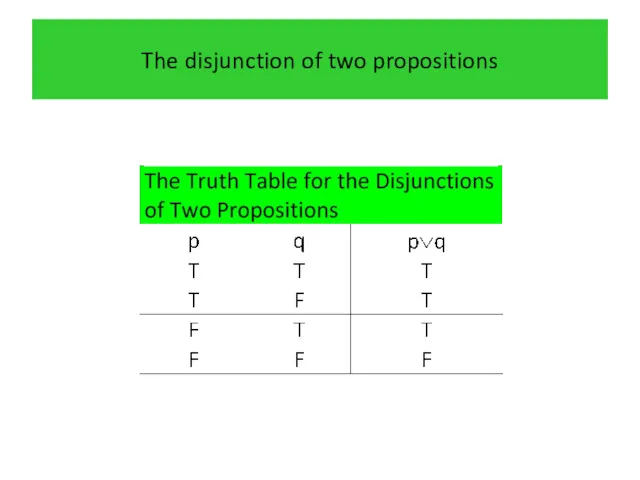
- 16. The disjunction of two propositions Definition 4 Let p and q be propositions. The disjunction of
- 17. The disjunction of two propositions
- 18. The disjunction of two propositions Example 5 Find the disjunction of the propositions p and q
- 19. The disjunction of two propositions Solution The disjunction of p and q, p∨q, is the proposition
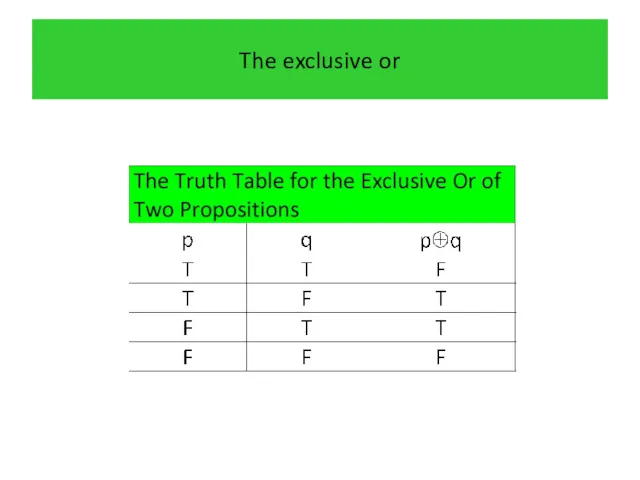
- 20. The exclusive or The use of the connective or in a disjunction corresponds to one of
- 21. The exclusive or On the other hand, we are using the exclusive or when we say
- 22. The exclusive or Definition 5 Let p and q be propositions. The exclusive or of p
- 23. The exclusive or
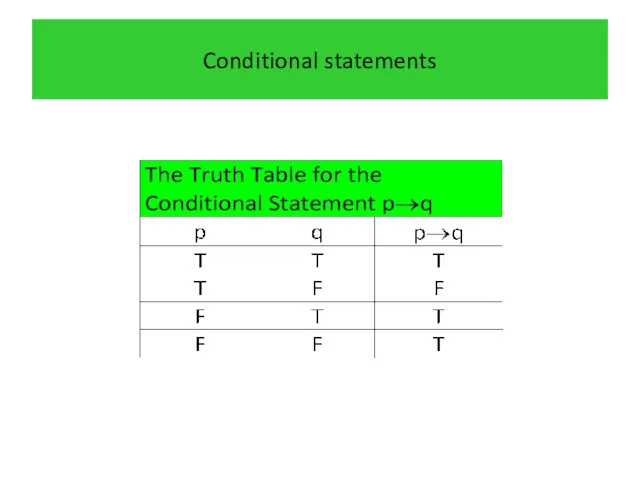
- 24. Conditional statements
- 25. Conditional statements
- 26. Conditional statements
- 27. Conditional statements
- 28. Conditional statements
- 29. Converse, contrapositive and inverse
- 30. Converse, contrapositive and inverse
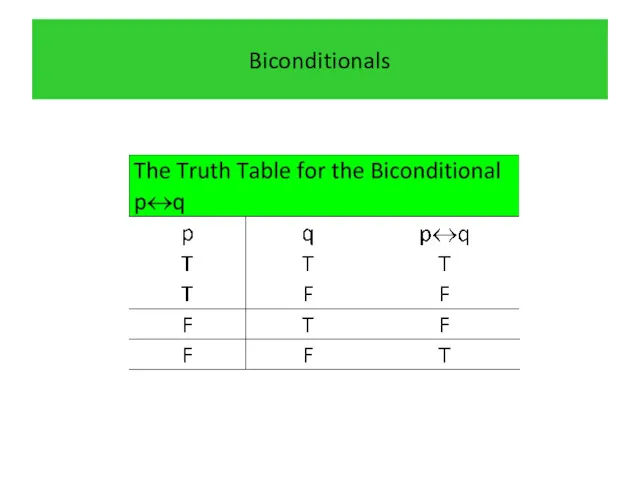
- 31. Biconditionals
- 32. Biconditionals
- 33. Biconditionals
- 34. Biconditionals
- 35. Truth tables of compound propositions We have now introduced four important logical connectives – conjunctions, disjunctions,
- 36. Truth tables of compound propositions We can use truth tables to determine the truth values of
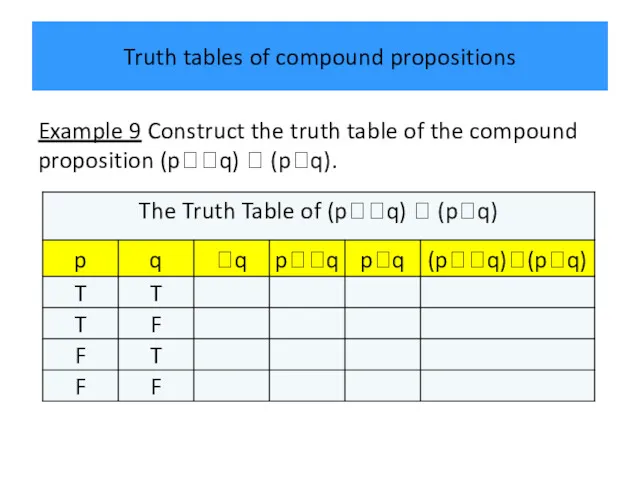
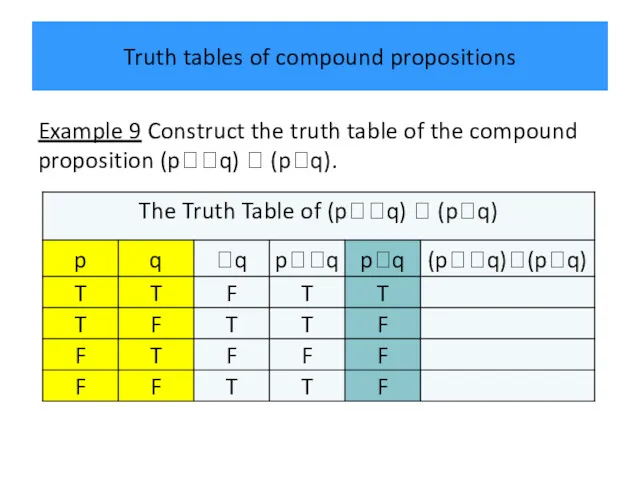
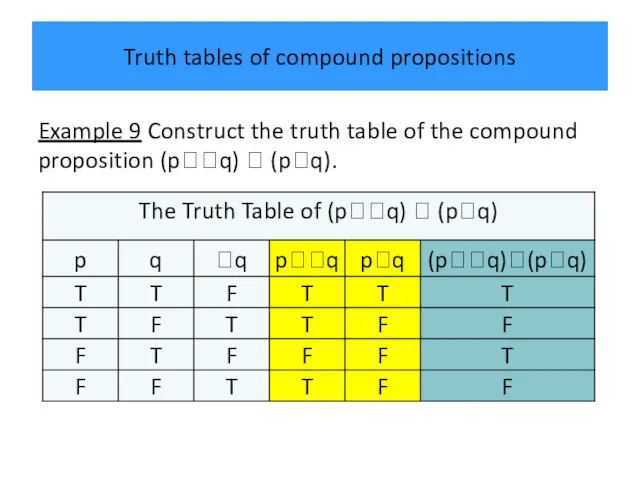
- 37. Truth tables of compound propositions Example 9 Construct the truth table of the compound proposition (pq)
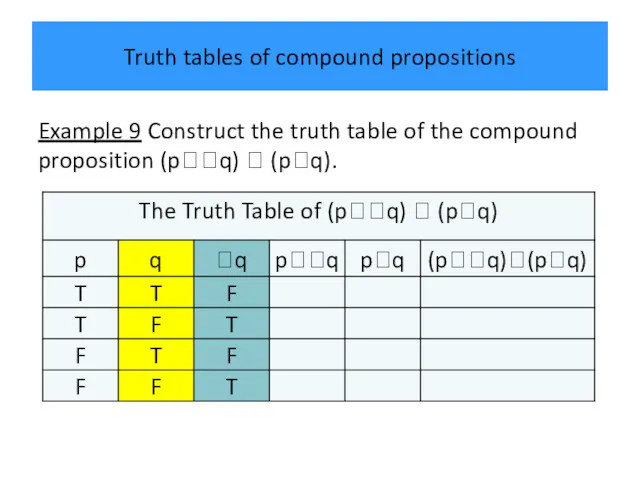
- 38. Truth tables of compound propositions Example 9 Construct the truth table of the compound proposition (pq)
- 39. Truth tables of compound propositions Example 9 Construct the truth table of the compound proposition (pq)
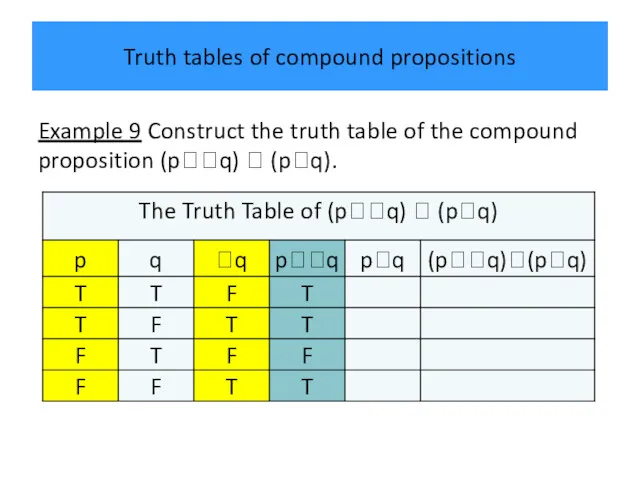
- 40. Truth tables of compound propositions Example 9 Construct the truth table of the compound proposition (pq)
- 41. Truth tables of compound propositions Example 9 Construct the truth table of the compound proposition (pq)
- 42. Truth tables of compound propositions Example 9 Construct the truth table of the compound proposition (pq)
- 43. Truth tables of compound propositions Example 9 Construct the truth table of the compound proposition (pq)
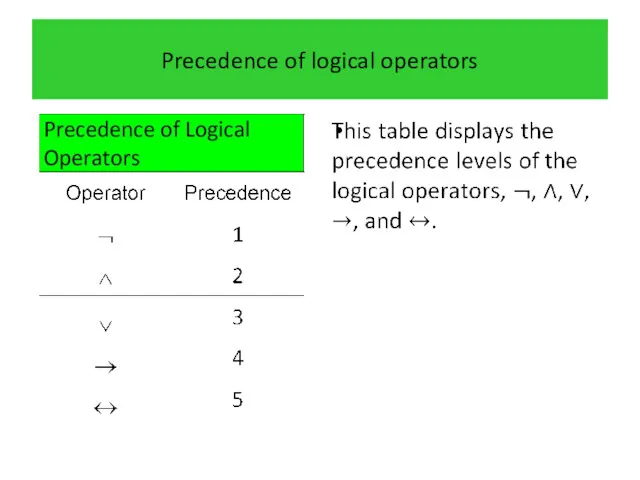
- 44. Precedence of logical operators
- 45. Precedence of logical operators
- 46. Precedence of logical operators
- 47. Precedence of logical operators Another general rule of precedence is that the conjunction operator takes precedence
- 48. Precedence of logical operators
- 49. Tautologies and contradictions Definition 8 A compound proposition that is always true, no matter what the
- 50. Tautologies and contradictions Example 10 We can construct examples of tautologies and contradictions using just one
- 51. Tautologies and contradictions
- 52. Logical equivalences
- 53. Logical equivalences One way to determine whether two compound propositions are equivalent is to use a
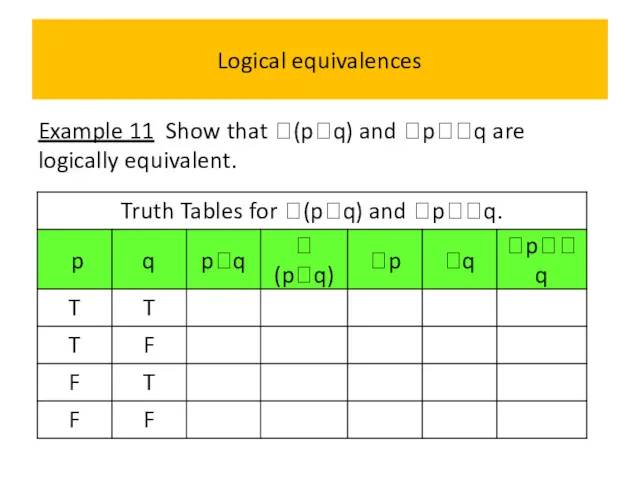
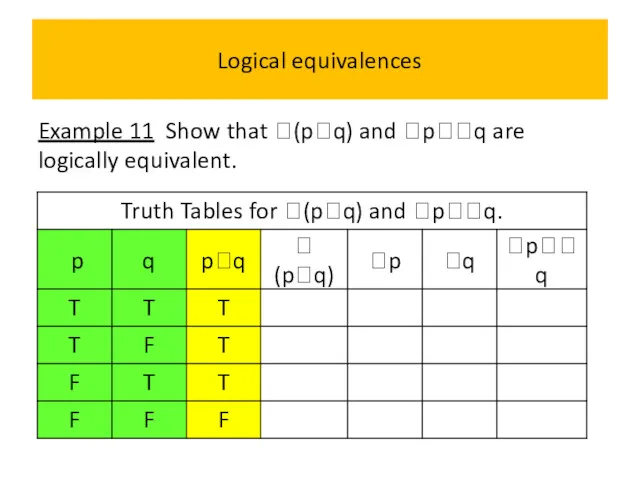
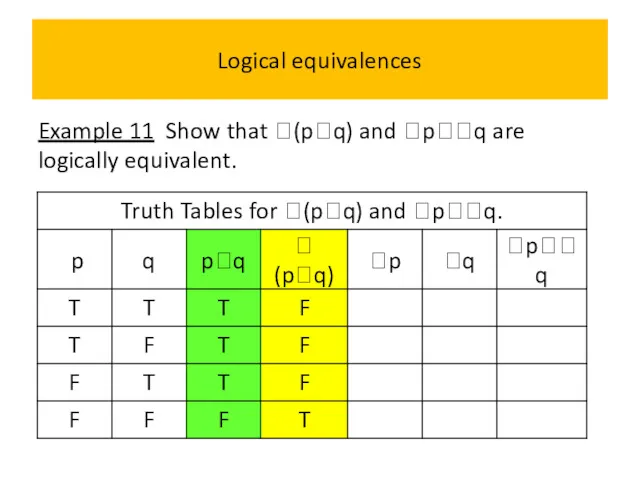
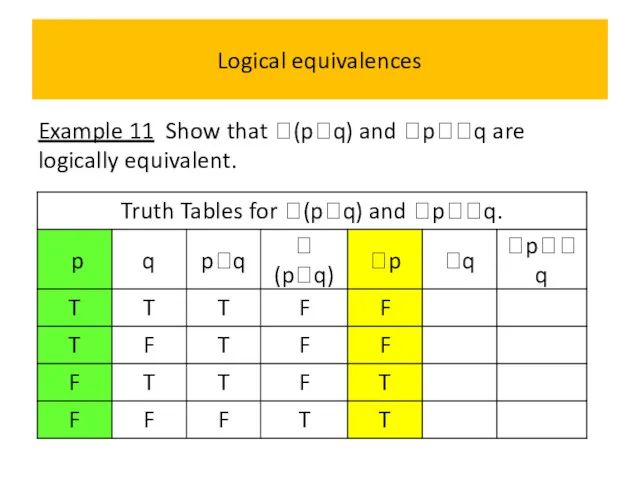
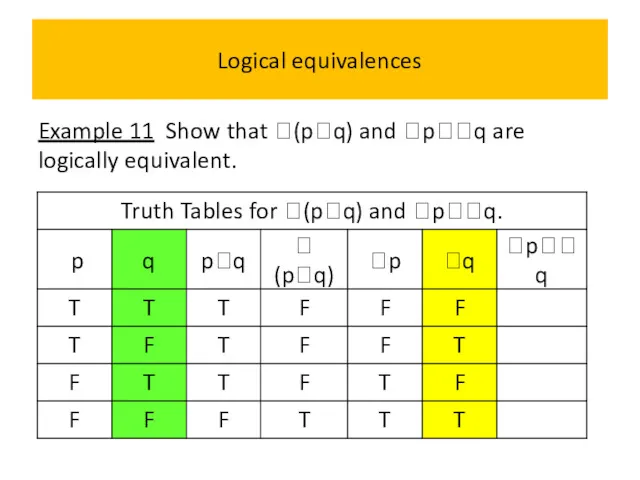
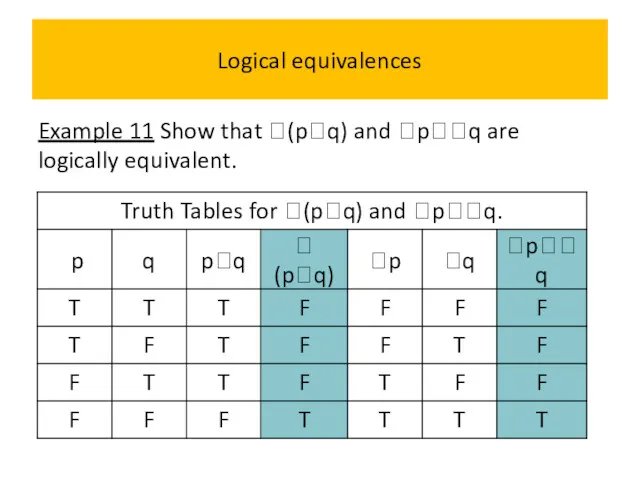
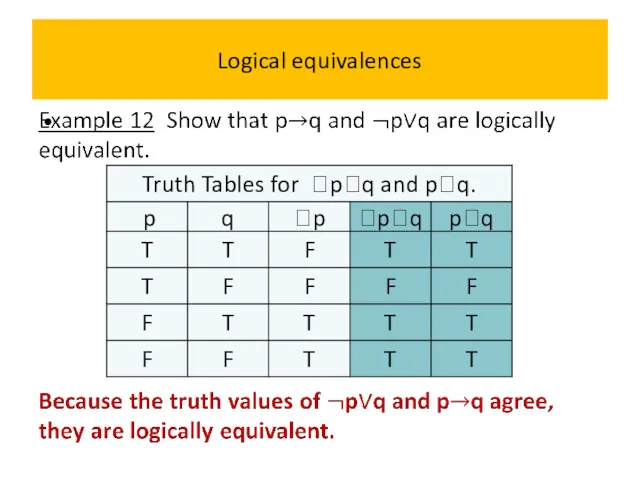
- 54. Logical equivalences Example 11 Show that (pq) and pq are logically equivalent.
- 55. Logical equivalences Example 11 Show that (pq) and pq are logically equivalent.
- 56. Logical equivalences Example 11 Show that (pq) and pq are logically equivalent.
- 57. Logical equivalences Example 11 Show that (pq) and pq are logically equivalent.
- 58. Logical equivalences Example 11 Show that (pq) and pq are logically equivalent.
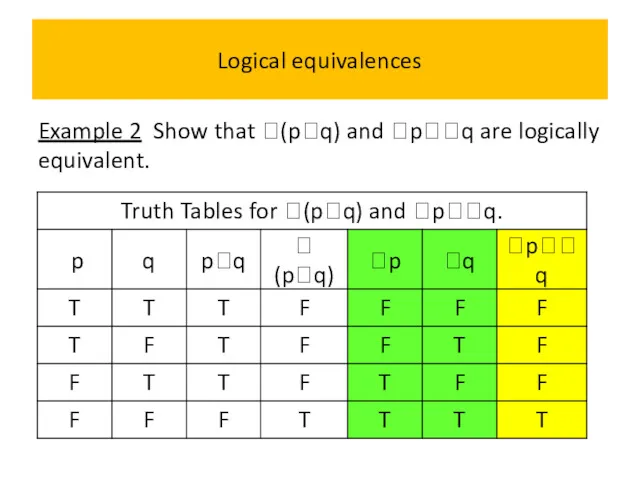
- 59. Logical equivalences Example 2 Show that (pq) and pq are logically equivalent.
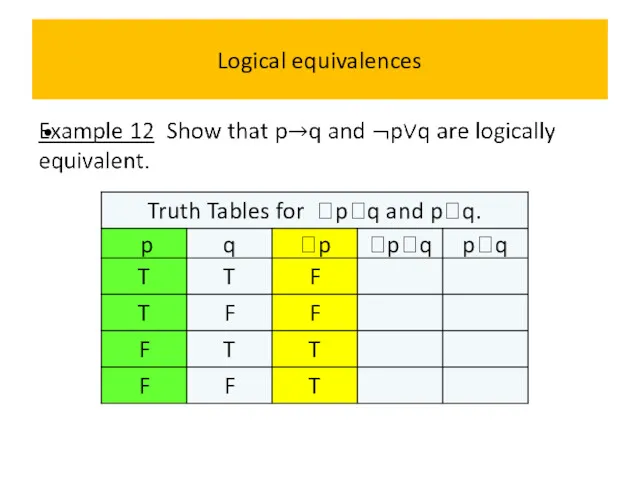
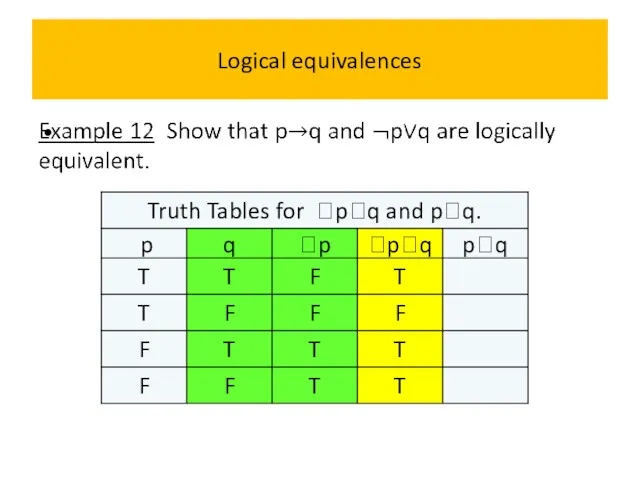
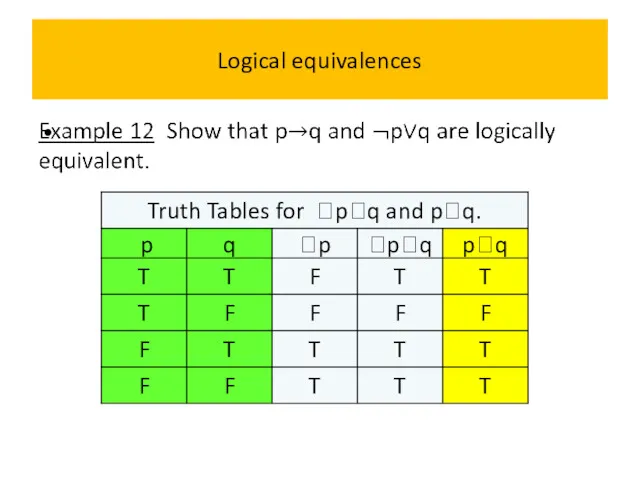
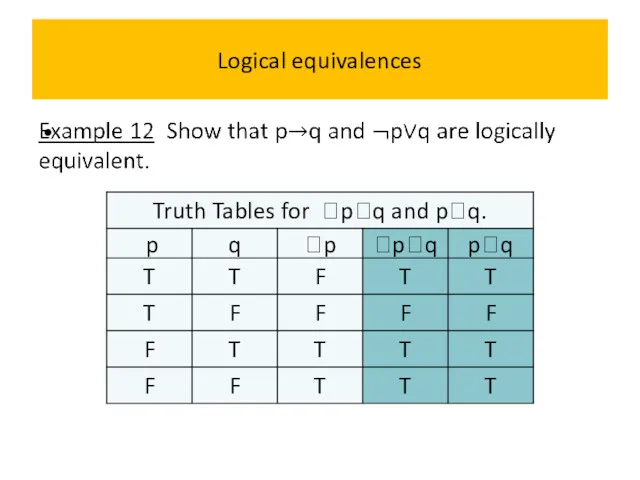
- 60. Logical equivalences Example 11 Show that (pq) and pq are logically equivalent.
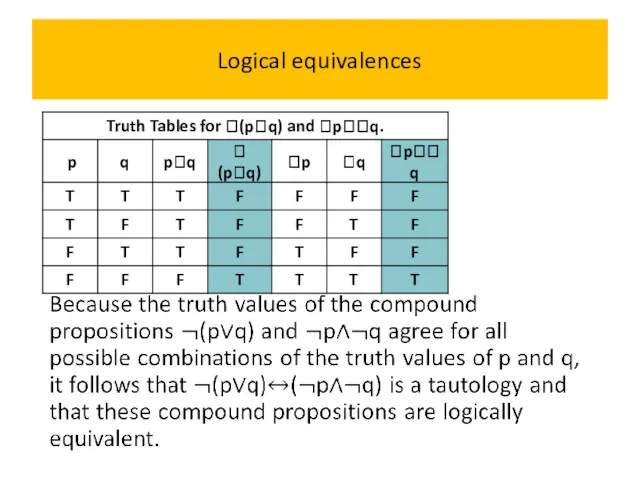
- 61. Logical equivalences
- 62. Logical equivalences (pq) pq This logical equivalence is one of the two De Morgan laws,
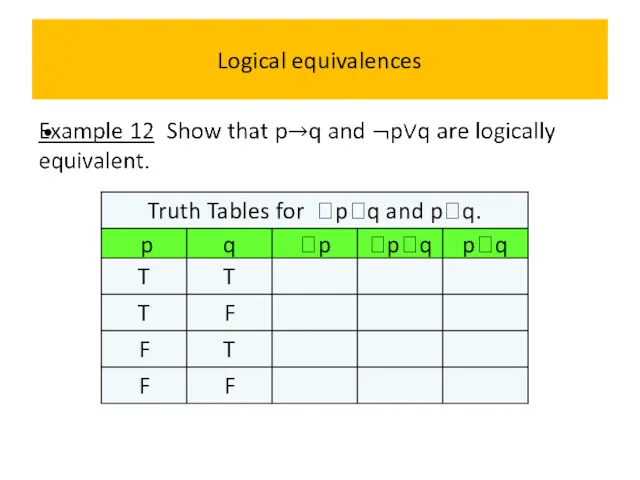
- 63. Logical equivalences
- 64. Logical equivalences
- 65. Logical equivalences
- 66. Logical equivalences
- 67. Logical equivalences
- 68. Logical equivalences
- 69. Logical equivalences
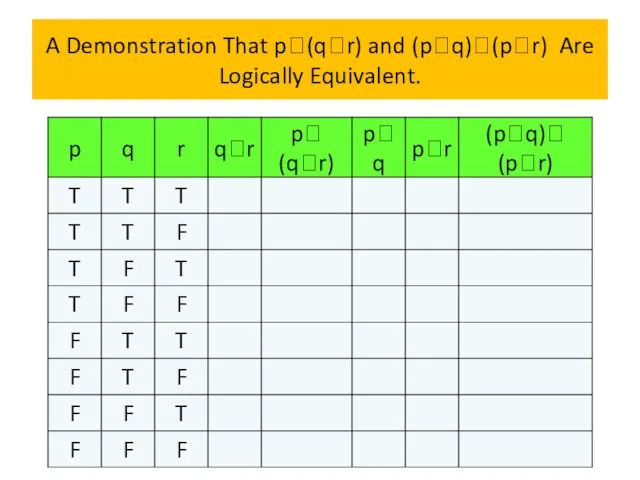
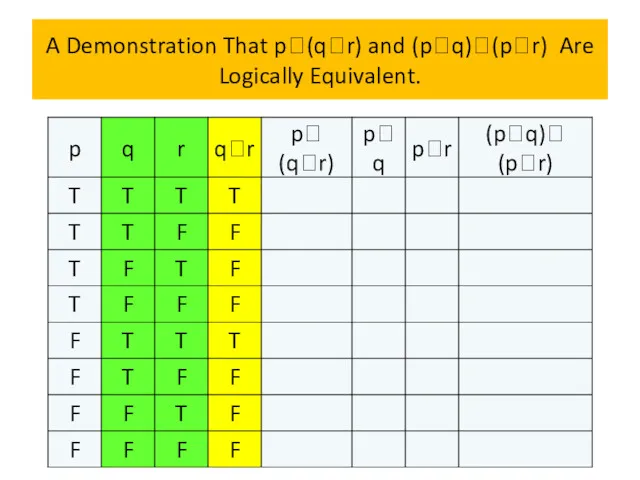
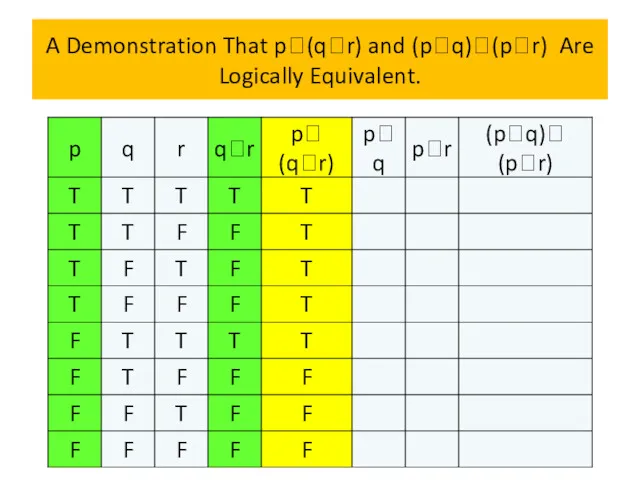
- 70. Logical equivalences We will now establish a logical equivalence of two compound propositions involving three different
- 71. Logical equivalences Example 13 Show that p∨(q∧r) and (p∨q)∧(p∨r) are logically equivalent. This is the distributive
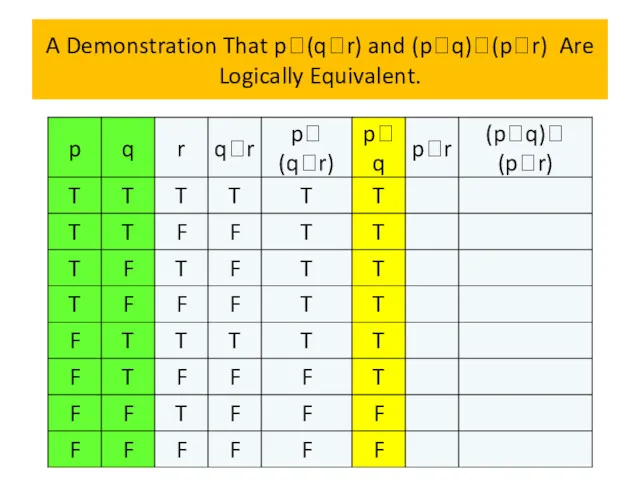
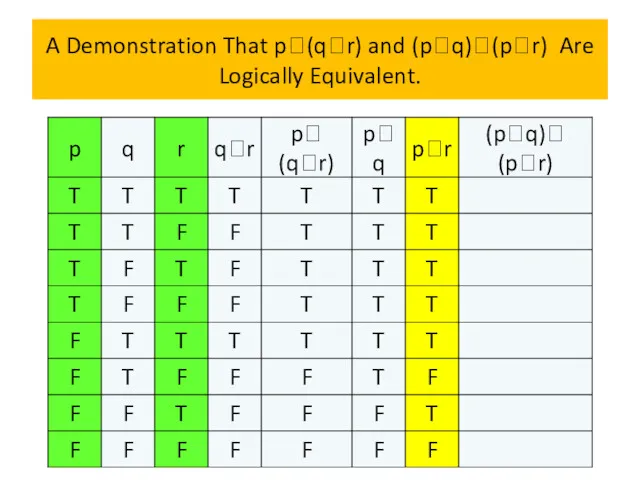
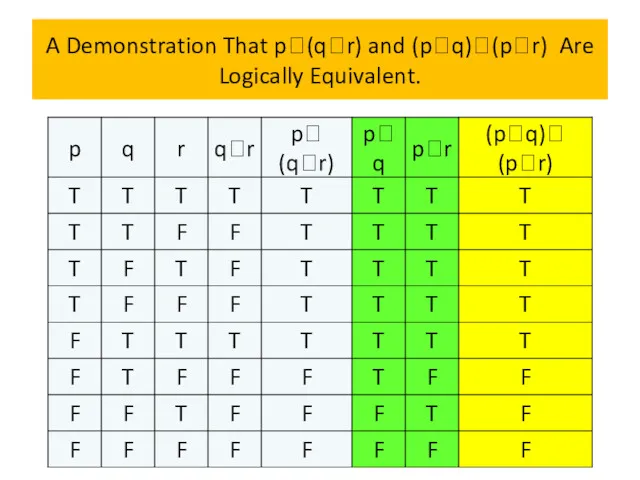
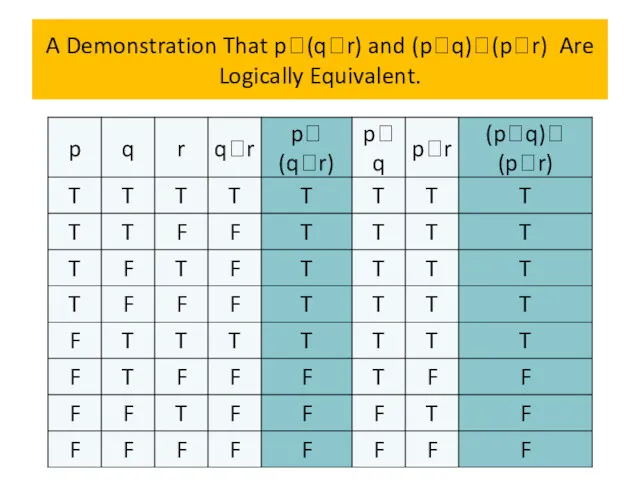
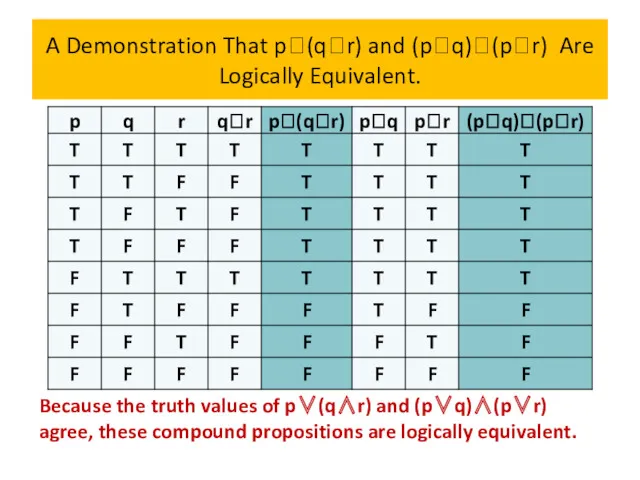
- 72. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 73. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 74. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 75. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 76. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 77. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 78. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent.
- 79. A Demonstration That p(qr) and (pq)(pr) Are Logically Equivalent. Because the truth values of p∨(q∧r) and
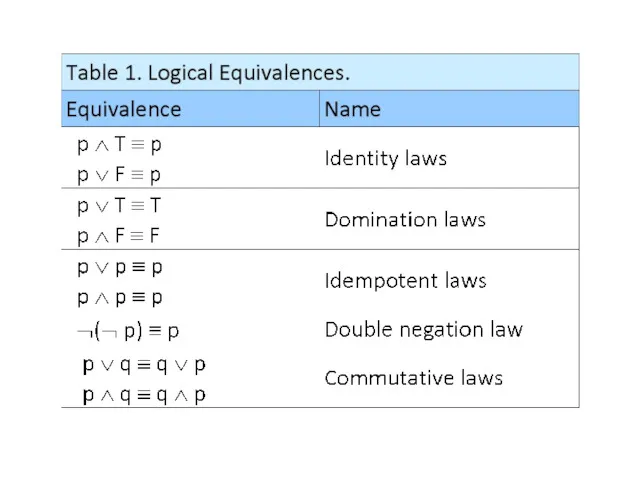
- 80. Logical equivalences Next table contains some important equivalences. In these equivalences, T denotes the compound proposition
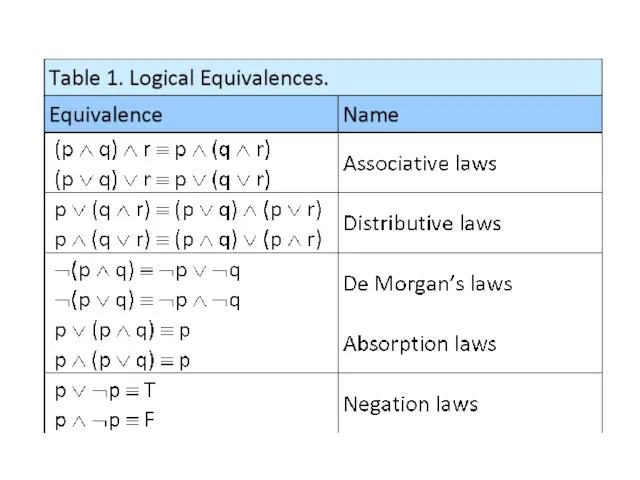
- 83. Logical equivalences
- 84. Logical equivalences We also display some useful equivalences for compound propositions involving conditional statements and biconditional
- 87. Using De Morgan’s Laws Example 13 Use De Morgan’s laws to express the negations of “Miguel
- 88. Using De Morgan’s Laws Example 13 Use De Morgan’s laws to express the negations of “Miguel
- 89. Constructing new logical equivalences The logical equivalences in Table 1, as well as any others that
- 90. Constructing new logical equivalences This technique is illustrated in Examples 14 – 16, where we also
- 91. Constructing new logical equivalences Example 14 Show that (p q) and p q are
- 92. Constructing new logical equivalences Example 14 Show that (p q) and p q are
- 93. Constructing new logical equivalences Example 15 Show that (p (p q)) and (p
- 94. Constructing new logical equivalences Example 15 Show that (p (p q)) and (p
- 95. Constructing new logical equivalences Example 16 Show that (p q) (p q) is
- 96. Propositional satisfiability Definition 10 A compound proposition is satisfiable if there is an assignment of truth
- 97. Propositional satisfiability Definition 11 When we find a particular assignment of truth values that makes a
- 98. Propositional satisfiability However, to show that a compound proposition is unsatisfiable, we need to show that
- 99. Propositional satisfiability Example 17 Determine whether each of the compound propositions (p q) (q
- 100. Propositional satisfiability
- 101. Satisfiability problem Many problems, in diverse areas such as robotics, software testing, computer-aided design, machine vision,
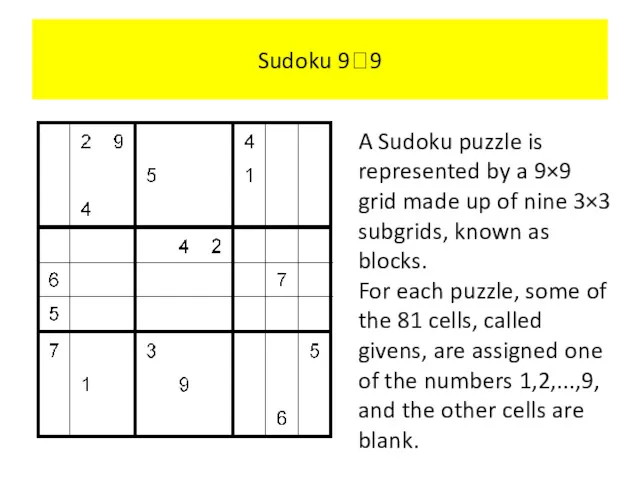
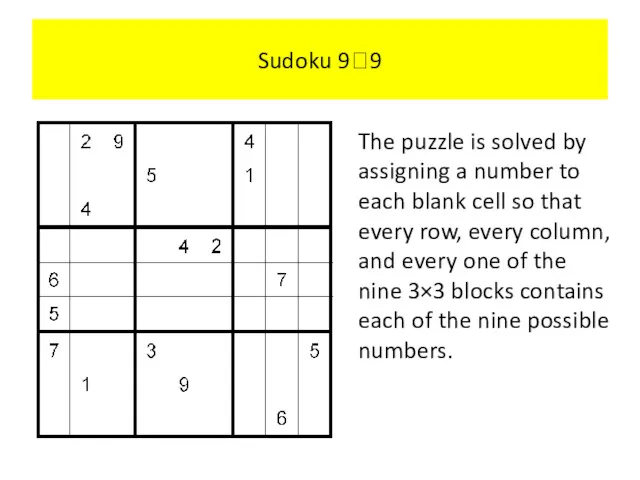
- 102. Sudoku 99 A Sudoku puzzle is represented by a 9×9 grid made up of nine 3×3
- 103. Sudoku 99 The puzzle is solved by assigning a number to each blank cell so that
- 105. Скачать презентацию

































































 Оформление списка литературы к научной работе
Оформление списка литературы к научной работе Строим свой сайт
Строим свой сайт Что такое “Платформер”
Что такое “Платформер” Компьютерная графика http://compgraph.tpu.ru/
Компьютерная графика http://compgraph.tpu.ru/ Интеллектуальные информационные системы. Классификация интеллектуальных информационных систем
Интеллектуальные информационные системы. Классификация интеллектуальных информационных систем Файловые системы. Работа с файлами в Windows API. Асинхронный и синхронный файловый ввод-вывод
Файловые системы. Работа с файлами в Windows API. Асинхронный и синхронный файловый ввод-вывод Oracle and/or its affiliates. Resources
Oracle and/or its affiliates. Resources Начальные сведения. Определение и основные понятия. Что могут содержать Web-страницы HTML теги?
Начальные сведения. Определение и основные понятия. Что могут содержать Web-страницы HTML теги? Операторы языка С++. Структура программы. Лекция 2
Операторы языка С++. Структура программы. Лекция 2 NP-складність і NP-повнота. Приклади наближених алгоритмів для NP-повних задач. Лекція 4
NP-складність і NP-повнота. Приклади наближених алгоритмів для NP-повних задач. Лекція 4 Основи Java Script. Масиви
Основи Java Script. Масиви Метод координат. Способы кодирования информации
Метод координат. Способы кодирования информации Архитектура приложений реального времени
Архитектура приложений реального времени Инструкция PackageAssistant. Помощник в настройке смартфонов
Инструкция PackageAssistant. Помощник в настройке смартфонов Автоматизоване створення та публікування веб-сайтів
Автоматизоване створення та публікування веб-сайтів Единый семинар фирмы 1С для бухгалтеров и руководителей
Единый семинар фирмы 1С для бухгалтеров и руководителей Технология хранения, обработки и анализа данных
Технология хранения, обработки и анализа данных Маршрутизация между VLAN
Маршрутизация между VLAN Робота зі ЗМІ
Робота зі ЗМІ Графический интерфейс пользователя операционной системы
Графический интерфейс пользователя операционной системы Internet
Internet Магнитные носители информации
Магнитные носители информации Школьная библиотека: Копилочка. Инновационные формы профессионального взаимодействия
Школьная библиотека: Копилочка. Инновационные формы профессионального взаимодействия Криптографические средства защиты информации
Криптографические средства защиты информации Создание учебных курсов в системе Moodle
Создание учебных курсов в системе Moodle STL алгоритмы
STL алгоритмы Что такое пиксель
Что такое пиксель Интернет: за и против
Интернет: за и против