Слайд 2

Quicksort I: Basic idea
Pick some number p from the array
Move all
numbers less than p to the beginning of the array
Move all numbers greater than (or equal to) p to the end of the array
Quicksort the numbers less than p
Quicksort the numbers greater than or equal to p
Слайд 3
![Quicksort II To sort a[left...right]: 1. if left 1.1. Partition](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/21012/slide-2.jpg)
Quicksort II
To sort a[left...right]:
1. if left < right:
1.1. Partition a[left...right] such
that:
all a[left...p-1] are less than a[p], and
all a[p+1...right] are >= a[p]
1.2. Quicksort a[left...p-1]
1.3. Quicksort a[p+1...right]
2. Terminate
Слайд 4

Partitioning (Quicksort II)
A key step in the Quicksort algorithm is partitioning
the array
We choose some (any) number p in the array to use as a pivot
We partition the array into three parts:
Слайд 5

Partitioning II
Choose an array value (say, the first) to use as
the pivot
Starting from the left end, find the first element that is greater than or equal to the pivot
Searching backward from the right end, find the first element that is less than the pivot
Interchange (swap) these two elements
Repeat, searching from where we left off, until done
Слайд 6
![Partitioning To partition a[left...right]: 1. Set pivot = a[left], l](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/21012/slide-5.jpg)
Partitioning
To partition a[left...right]:
1. Set pivot = a[left], l = left +
1, r = right;
2. while l < r, do
2.1. while l < right & a[l] < pivot , set l = l + 1
2.2. while r > left & a[r] >= pivot , set r = r - 1
2.3. if l < r, swap a[l] and a[r]
3. Set a[left] = a[r], a[r] = pivot
4. Terminate
Слайд 7

Example of partitioning
choose pivot: 4 3 6 9 2 4 3 1
2 1 8 9 3 5 6
search: 4 3 6 9 2 4 3 1 2 1 8 9 3 5 6
swap: 4 3 3 9 2 4 3 1 2 1 8 9 6 5 6
search: 4 3 3 9 2 4 3 1 2 1 8 9 6 5 6
swap: 4 3 3 1 2 4 3 1 2 9 8 9 6 5 6
search: 4 3 3 1 2 4 3 1 2 9 8 9 6 5 6
swap: 4 3 3 1 2 2 3 1 4 9 8 9 6 5 6
search: 4 3 3 1 2 2 3 1 4 9 8 9 6 5 6 (left > right)
swap with pivot: 1 3 3 1 2 2 3 4 4 9 8 9 6 5 6
Слайд 8
![The partition method (Java) static int partition(int[] a, int left,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/21012/slide-7.jpg)
The partition method (Java)
static int partition(int[] a, int left, int
right) {
int p = a[left], l = left + 1, r = right;
while (l < r) {
while (l < right && a[l] < p) l++;
while (r > left && a[r] >= p) r--;
if (l < r) {
int temp = a[l]; a[l] = a[r]; a[r] = temp;
}
}
a[left] = a[r];
a[r] = p;
return r;
}
Слайд 9
![The quicksort method (in Java) static void quicksort(int[] array, int left, int right) { if (left](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/21012/slide-8.jpg)
The quicksort method (in Java)
static void quicksort(int[] array, int left, int
right) {
if (left < right) {
int p = partition(array, left, right);
quicksort(array, left, p - 1);
quicksort(array, p + 1, right);
}
}
Слайд 10

Analysis of quicksort—best case
Suppose each partition operation divides the array almost
exactly in half
Then the depth of the recursion in log2n
Because that’s how many times we can halve n
However, there are many recursions!
How can we figure this out?
We note that
Each partition is linear over its subarray
All the partitions at one level cover the array
Слайд 11
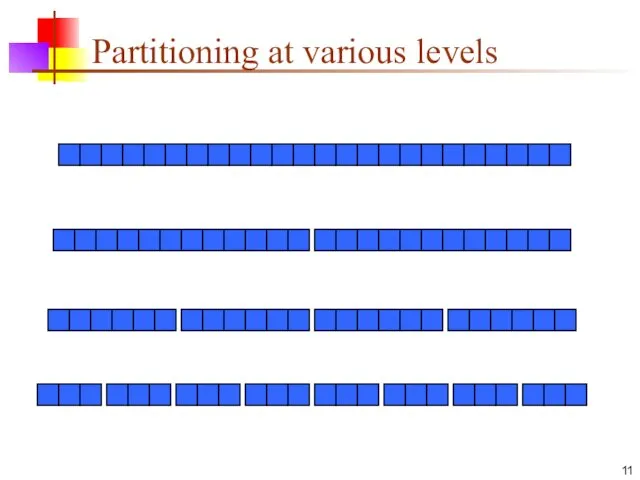
Partitioning at various levels
Слайд 12

Best case II
We cut the array size in half each
time
So the depth of the recursion in log2n
At each level of the recursion, all the partitions at that level do work that is linear in n
O(log2n) * O(n) = O(n log2n)
Hence in the average case, quicksort has time complexity O(n log2n)
What about the worst case?
Слайд 13

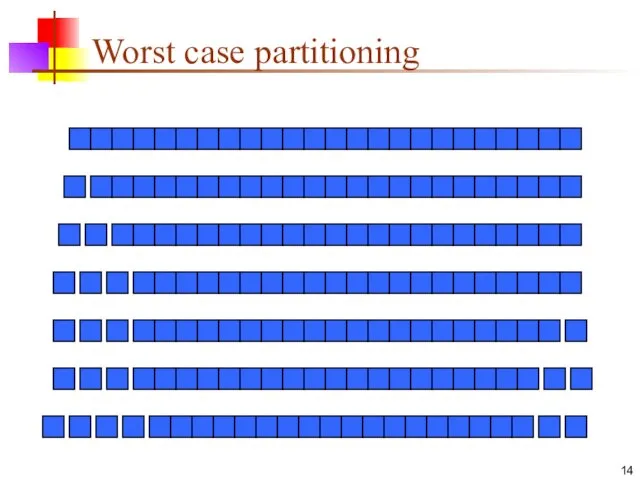
Worst case
In the worst case, partitioning always divides the size n
array into these three parts:
A length one part, containing the pivot itself
A length zero part, and
A length n-1 part, containing everything else
We don’t recur on the zero-length part
Recurring on the length n-1 part requires (in the worst case) recurring to depth n-1
Слайд 14
Слайд 15

Worst case for quicksort
In the worst case, recursion may be n
levels deep (for an array of size n)
But the partitioning work done at each level is still n
O(n) * O(n) = O(n2)
So worst case for Quicksort is O(n2)
When does this happen?
There are many arrangements that could make this happen
Here are two common cases:
When the array is already sorted
When the array is inversely sorted (sorted in the opposite order)
Слайд 16

Typical case for quicksort
If the array is sorted to begin with,
Quicksort is terrible: O(n2)
It is possible to construct other bad cases
However, Quicksort is usually O(n log2n)
The constants are so good that Quicksort is generally the fastest algorithm known
Most real-world sorting is done by Quicksort
Слайд 17

Improving the interface
We’ve defined the Quicksort method as
static void quicksort(int[]
array, int left, int right) { … }
So we would have to call it as
quicksort(myArray, 0, myArray.length)
That’s ugly!
Solution:
static void quicksort(int[] array) {
quicksort(array, 0, array.length);
}
Now we can make the original (3-argument) version private
Слайд 18

Tweaking Quicksort
Almost anything you can try to “improve” Quicksort will actually
slow it down
One good tweak is to switch to a different sorting method when the subarrays get small (say, 10 or 12)
Quicksort has too much overhead for small array sizes
For large arrays, it might be a good idea to check beforehand if the array is already sorted
But there is a better tweak than this
Слайд 19

Picking a better pivot
Before, we picked the first element of the
subarray to use as a pivot
If the array is already sorted, this results in O(n2) behavior
It’s no better if we pick the last element
We could do an optimal quicksort (guaranteed
O(n log n)) if we always picked a pivot value that exactly cuts the array in half
Such a value is called a median: half of the values in the array are larger, half are smaller
The easiest way to find the median is to sort the array and pick the value in the middle (!)
Слайд 20

Median of three
Obviously, it doesn’t make sense to sort the array
in order to find the median to use as a pivot
Instead, compare just three elements of our (sub)array—the first, the last, and the middle
Take the median (middle value) of these three as pivot
It’s possible (but not easy) to construct cases which will make this technique O(n2)
Suppose we rearrange (sort) these three numbers so that the smallest is in the first position, the largest in the last position, and the other in the middle
This lets us simplify and speed up the partition loop
Слайд 21

Final comments
Quicksort is the fastest known sorting algorithm
For optimum efficiency, the
pivot must be chosen carefully
“Median of three” is a good technique for choosing the pivot
However, no matter what you do, there will be some cases where Quicksort runs in O(n2) time

![Quicksort II To sort a[left...right]: 1. if left 1.1. Partition](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/21012/slide-2.jpg)


![Partitioning To partition a[left...right]: 1. Set pivot = a[left], l](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/21012/slide-5.jpg)

![The partition method (Java) static int partition(int[] a, int left,](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/21012/slide-7.jpg)
![The quicksort method (in Java) static void quicksort(int[] array, int left, int right) { if (left](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/21012/slide-8.jpg)












 Позиционные системы счисления
Позиционные системы счисления Локальные сети. Параметры сетей и их стандарты
Локальные сети. Параметры сетей и их стандарты Сбор и подготовка данных
Сбор и подготовка данных Современные накопители информации, используемые в вычислительной технике
Современные накопители информации, используемые в вычислительной технике Использование технологии веб-квест как средство развития познавательных и творческих способностей учащихся
Использование технологии веб-квест как средство развития познавательных и творческих способностей учащихся Блочные алгоритмы. Блочное шифрование. Сравнение блочных и поточных шифров. Предпосылки создания шифра Фейстеля
Блочные алгоритмы. Блочное шифрование. Сравнение блочных и поточных шифров. Предпосылки создания шифра Фейстеля Параллельное программирование. С++. Thread Support Library. Atomic Operations Library
Параллельное программирование. С++. Thread Support Library. Atomic Operations Library Функции в Excel
Функции в Excel Организация и средства информационных технологий обеспечения управленческой деятельности
Организация и средства информационных технологий обеспечения управленческой деятельности Поиск публикаций и показатели деятельности ученого в Web of Science
Поиск публикаций и показатели деятельности ученого в Web of Science Бездротові мережі
Бездротові мережі Занятие 1. Знакомство с программой Adobe Photoshop
Занятие 1. Знакомство с программой Adobe Photoshop Microsoft Visual Studio — линейка продуктов компании Microsoft
Microsoft Visual Studio — линейка продуктов компании Microsoft Операторы цикла
Операторы цикла Понятие об информации. Представление информации. Информационная деятельность человека.
Понятие об информации. Представление информации. Информационная деятельность человека. Автоматизоване створення запитів у базі даних
Автоматизоване створення запитів у базі даних Архітектура операційних систем
Архітектура операційних систем Windows System Programming
Windows System Programming Личный кабинет
Личный кабинет Мир станочника. Аддитивные технологии и 3D-сканирование
Мир станочника. Аддитивные технологии и 3D-сканирование Методы и средства защиты программ от компьютерных вирусов
Методы и средства защиты программ от компьютерных вирусов 46_Yaroslavskaya_Sasha
46_Yaroslavskaya_Sasha Локальные и глобальные сети ЭВМ. Защита информации в сетях. (Тема 6)
Локальные и глобальные сети ЭВМ. Защита информации в сетях. (Тема 6) Godseeker. Игра
Godseeker. Игра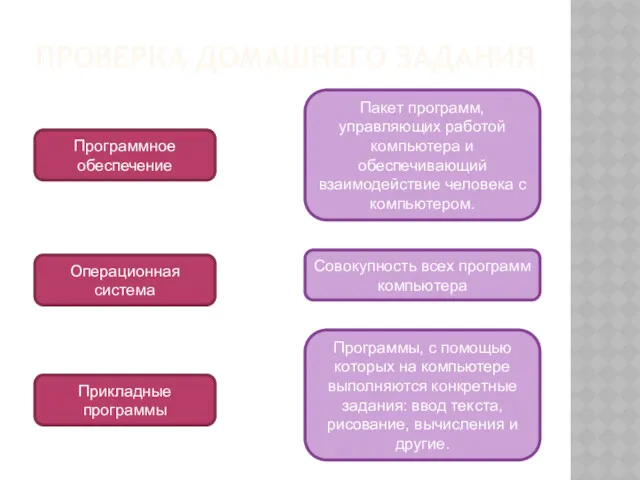 Рабочий стол. Управление компьютером с помощью мыши
Рабочий стол. Управление компьютером с помощью мыши Проектирование изделий из листового металла в NX
Проектирование изделий из листового металла в NX Эти люди изменили мир
Эти люди изменили мир Электронные ресурсы для детей и юношества в общедоступных библиотеках: создание и использование
Электронные ресурсы для детей и юношества в общедоступных библиотеках: создание и использование