Содержание
- 2. План Системы счисления. Классификация Арифметика в двоичной системе счисления Представление чисел в памяти компьютера
- 3. Система счисления Алфавит Х из р символов и правила записи и обработки чисел с помощью символов
- 4. Система счисления и кодирование Любая система счисления – это система кодирования числовых величин, позволяющая выполнять операции
- 5. Классификация СС Непозиционные Вес цифры (или символа алфавита) не зависит от ее места в записи числа
- 6. Непозиционные СС I = 1 V = 5 Х = 10 L = 50 С =
- 7. Непозиционные СС Примеры римских чисел: III = 3, IV = 4, V = 5, VI =
- 8. Все позиционные системы счисления строятся по общему принципу: определяется величина q – основание системы, а любое
- 9. Позиционные СС Пусть q - натуральное число большее 1 и M={0, 1, …, q-1}. Говорят, что
- 10. Если каждое число множества M={0, 1, …, q-1} обозначено специальным символом, то эти символы называются цифрами
- 11. Принятая система записи числа основана на том, что q единиц каждого разряда объединяются в одну единицу
- 12. Наиболее используемые в информатике системы счисления: двоичная, над алфавитом Х = {0,1}; восьмеричная, над Х =
- 13. Примеры: 11012 = 1*23 + 1*22 + 0*21 + 1*20 1578 = 1*82 + 5*81 +
- 14. Перевод чисел Общая задача перевода чисел из одной системы счисления в другую: Дано: x=(pnpn-1…p0p-1p-2…)P pi –
- 15. Перевод Q->P Запись и вычисление значения полинома X=xnqn+xn-1qn-1+…+x1q1+x0q0+x-1q-1+…+x-mq-m где все цифры xi и число q заменяются
- 16. Пример: Перевести (371)8 в Х10 Перевести (AF,4)16 в Х10 (371)8 = (3·82+7·81+1·80)10 = (3·64+7·8+1)10 = (249)10
- 17. Перевод целой части числа Перевод дробной части числа (его мантиссы) Перевод P->Q
- 18. N – целое число в p-ичной системе счисления. N=(qsqs-1…q1q0)Q, где искомые цифры определяются по следующим рекуррентным
- 19. Пример: Перевести N=(3060)10 в X16 3060 | 16 3056 191 |16 4 176 11 | 16
- 20. Пусть х - правильная дробь (0 Тогда х=(0,q-1q-2…q-m)Q, где искомые цифры определяются по следующим рекурентным формулам:
- 21. Пример: Перевести N=(0,2)10 в X2 0 2 2 0 4 2 0 8 2 1 6
- 22. Перевод произвольных чисел, то есть чисел, содержащих целую и дробную части, осуществляется в два этапа. Отдельно
- 23. Системы счисления, в которых каждый коэффициент p-ичного разложения числа записывается в q-ичной системе, q Смешанные СС
- 24. 92510 в двоично-десятичной системе записывается в виде 1001 0010 0101 Эта запись отличается от двоичного изображения
- 25. Пусть p=qL, (L – целое положительное число). Тогда запись какого либо числа в p-q-ичной системе счисления
- 26. Системы счисления с основанием 2
- 27. Примеры:
- 28. Примеры:
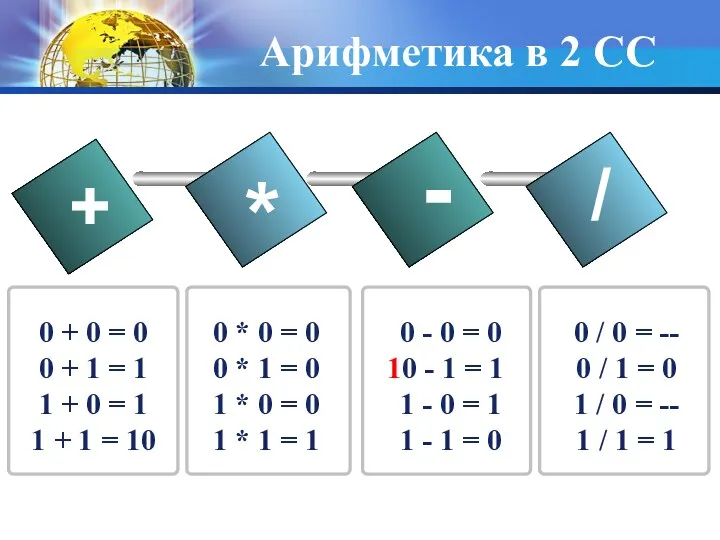
- 29. Арифметика в 2 СС + * - / 0 + 0 = 0 0 + 1
- 30. Обратный код числа Обратным кодом числа в системе с основанием р называется число в этой системе,
- 31. Пример: Двоичное число: 10011 Обратный код: 01100
- 32. Дополнительный код числа Дополнительный код = обратный код + единица в младшем разряде
- 33. Пример: Двоичное число: 10011 Обратный код: 01100 Дополнительный код: 01100 + 1 -------- 01101
- 34. Вычитание с дополнительным кодом A-B, если A>B: Найти дополнительный код вычитаемого такой же разрядности, как и
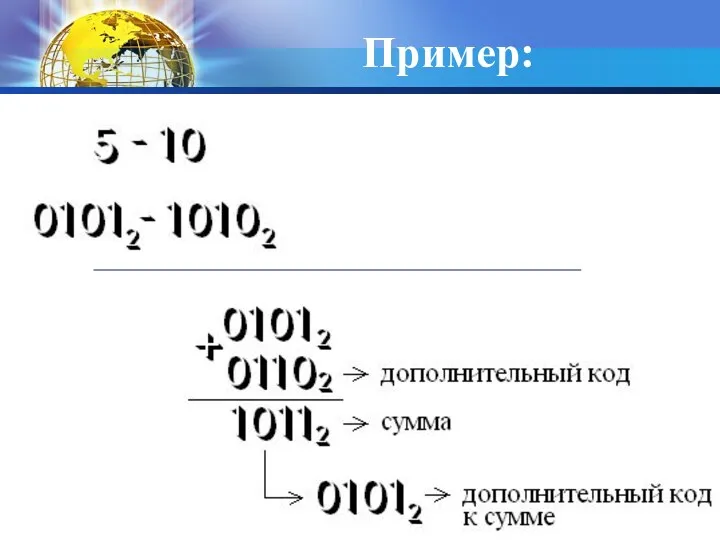
- 35. Пример:
- 36. Вычитание с дополнительным кодом A-B, если A Найти дополнительный код вычитаемого такой же разрядности, как и
- 37. Пример:
- 38. Представление чисел При проектировании ЭВМ, создании инструментального и прикладного программного обеспечения разработчикам приходится решать вопрос о
- 39. Представление чисел Запись целочисленных данных в запоминающем устройстве ЭВМ не представляет затруднений: число переводится в двоичную
- 40. Представление чисел Для вещественных данных обычно используются две формы записи: число с фиксированной точкой число с
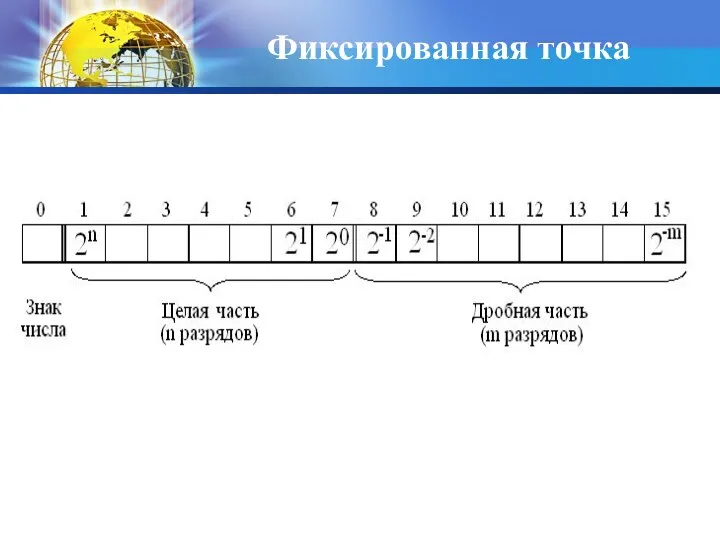
- 41. Фиксированная точка Форма записи числа с фиксированной точкой использовалась в основном на ранних этапах развития вычислительной
- 42. Фиксированная точка
- 43. Фиксированная точка Достоинства Недостатки Простота выполнения арифметических операций, высокая точность изображения чисел. небольшой диапазон представления чисел.
- 44. Плавающая точка Представление чисел с плавающей точкой – полулогарифмическая форма записи числа: N = ± mq
- 45. Плавающая точка Положение точки определяется значением порядка p. С изменением порядка точка перемещается (плавает) влево или
- 46. Пример: Влево: 12510 = =12.5*101 =1.25*102 =0.125*103 =0.0125*104 … Вправо: 12510 = =1250*10-1 =12500*10-2 =125000*10-3 =1250000*10-4
- 47. Плавающая точка Для установления однозначности при записи чисел принята нормализованная форма записи числа. Мантисса нормализованного числа
- 48. Плавающая точка
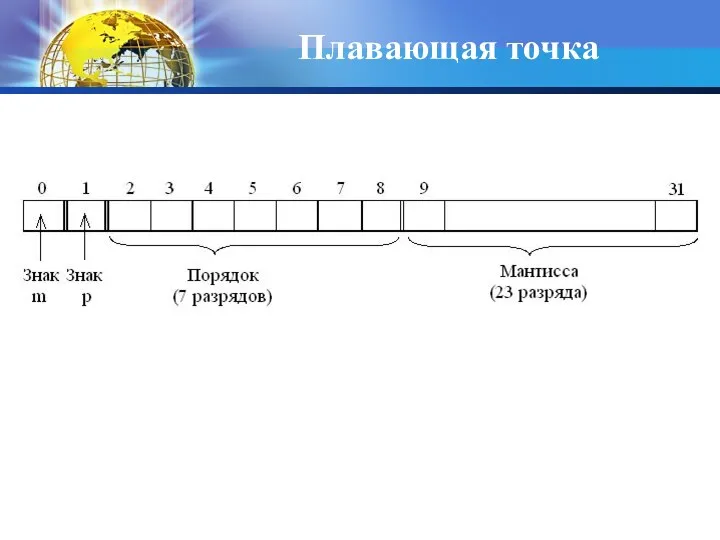
- 49. Плавающая точка Для представления чисел в машинном слове выделяют группы разрядов для изображения: мантиссы, порядка, знака
- 50. Плавающая точка
- 51. Пример: Число А=-3.510=-11.12=-0.111·1010
- 52. Плавающая точка Максимальным числом представимым в формате слова будет A=(0.1111...1·101111111)2=(1·2127)10
- 53. Плавающая точка Числа с плавающей точкой позволяют увеличить диапазон обрабатываемых чисел, но при этом точность изображения
- 55. Скачать презентацию
















































 Продукты IBM для разработки программных приложений. (Тема 9)
Продукты IBM для разработки программных приложений. (Тема 9) Основы программирования на C++
Основы программирования на C++ Единая сеть электросвязи РФ
Единая сеть электросвязи РФ Построение и исследование физической модели
Построение и исследование физической модели Базовые требования при подготовке презентаций
Базовые требования при подготовке презентаций Максимально эффективное использование ScienceDirect
Максимально эффективное использование ScienceDirect Подготовка школьников к ЕГЭ по информатике
Подготовка школьников к ЕГЭ по информатике Презентация к уроку Цикл с постусловием
Презентация к уроку Цикл с постусловием История серии видеоигры: Grand Theft Auto
История серии видеоигры: Grand Theft Auto Основы программирования на Python
Основы программирования на Python Онлайн сервис
Онлайн сервис Django. Запись данных. Урок 11
Django. Запись данных. Урок 11 Презентация к уроку Тексты в компьютерной памяти
Презентация к уроку Тексты в компьютерной памяти Информационная модель объекта
Информационная модель объекта Инструмент гарантированного доступа к госзакупкам. Портал поставщиков
Инструмент гарантированного доступа к госзакупкам. Портал поставщиков Обзор вариантов установки программ
Обзор вариантов установки программ конспект урока по информатике 9 класс по теме: Операторы ветвления+презентация
конспект урока по информатике 9 класс по теме: Операторы ветвления+презентация класс. 04.02.22
класс. 04.02.22 Вероятностный подход к определению количества информации
Вероятностный подход к определению количества информации Сети мобильной связи нового поколения. Лекция 7. Подсистема IP-мультимедиа (IMS)
Сети мобильной связи нового поколения. Лекция 7. Подсистема IP-мультимедиа (IMS) Программа курса “Введение в тестирование ПО”. Динамическое тестирование
Программа курса “Введение в тестирование ПО”. Динамическое тестирование Модели объектов. Моделирование
Модели объектов. Моделирование Мобильные вирусы и антивирусы
Мобильные вирусы и антивирусы Графикалық редакциялау
Графикалық редакциялау Проектирование программных средств
Проектирование программных средств 10 Useful, Weird or Entertaining Websites to Waste Time On
10 Useful, Weird or Entertaining Websites to Waste Time On Компьютерная графика
Компьютерная графика Программирование на языке Си
Программирование на языке Си