Содержание
- 2. Problem There is array A with N positive integers. Segment of array – a sequence of
- 3. 1. Very primitive solution Sum elements for each pair (L, R). for (int i = 0;
- 4. 2. Primitive solution Notice that sum(L, R) = sum(L, R-1)+A[R] If sum(L, R1)>D then sum(L, R2)>D
- 5. 3. Good solution Notice that it’s enough to find maxR(L) = max(R) such sum(L, R) D
- 6. 3. Good solution prefixSum[0] = a[0]; for (int i = 1; i prefixSum[i] = prefixSum[i -
- 7. 4. Best solution Notice that maxR(L)>=maxR(L-1). So we can start finding maxR(L) from maxR(L-1). In this
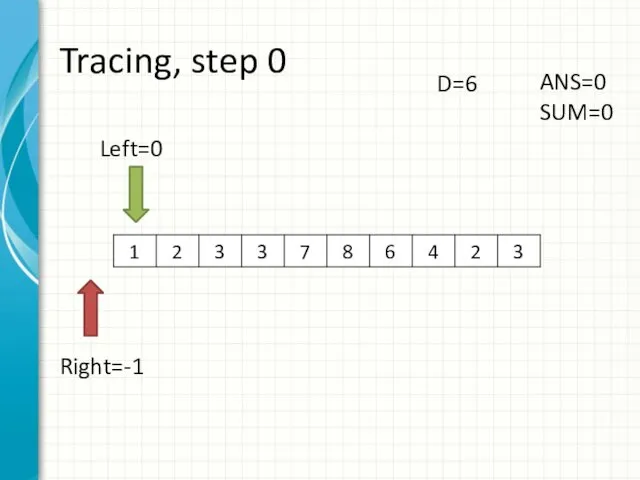
- 8. Tracing, step 0 Left=0 Right=-1 ANS=0 SUM=0 D=6
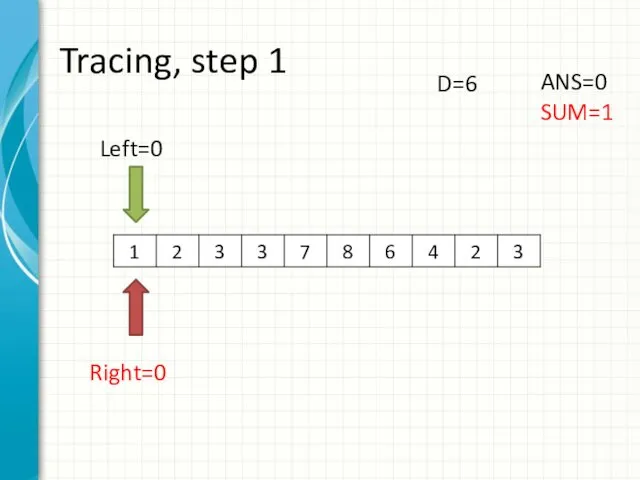
- 9. Tracing, step 1 Left=0 Right=0 ANS=0 SUM=1 D=6
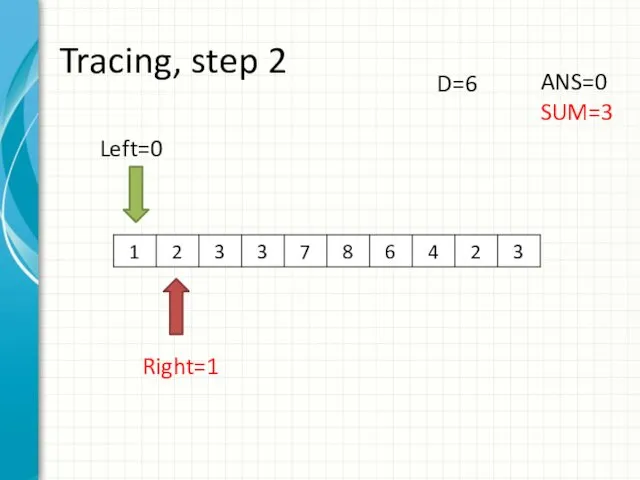
- 10. Tracing, step 2 Left=0 Right=1 ANS=0 SUM=3 D=6
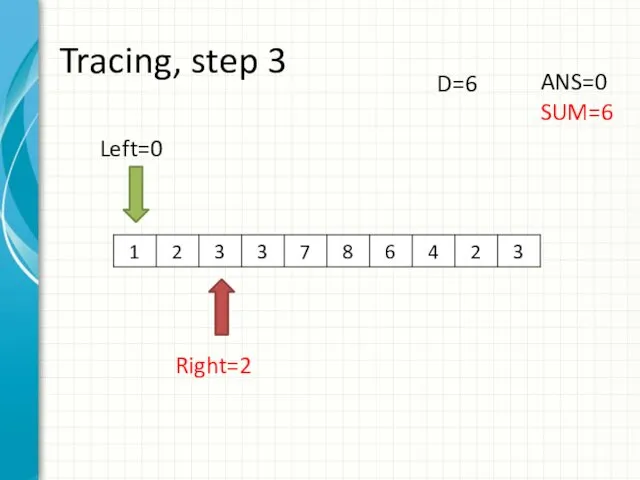
- 11. Tracing, step 3 Left=0 Right=2 ANS=0 SUM=6 D=6
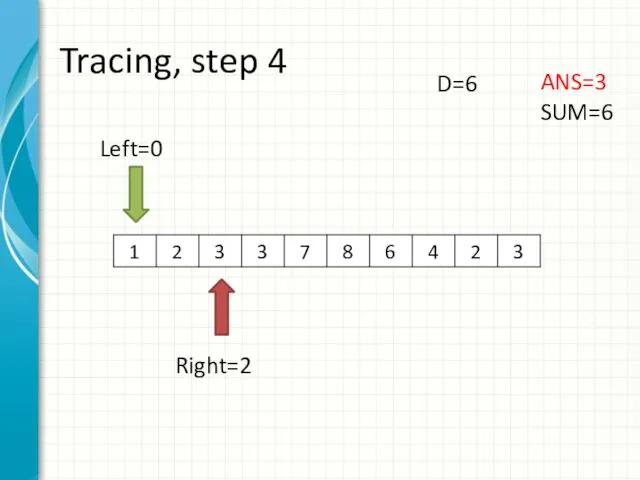
- 12. Tracing, step 4 Left=0 Right=2 ANS=3 SUM=6 D=6
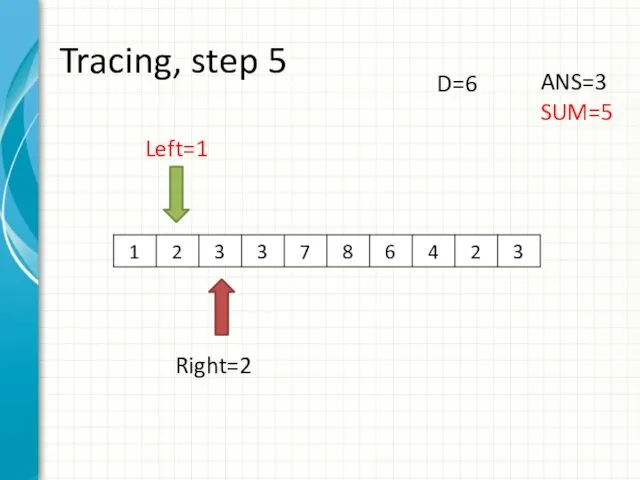
- 13. Tracing, step 5 Left=1 Right=2 ANS=3 SUM=5 D=6
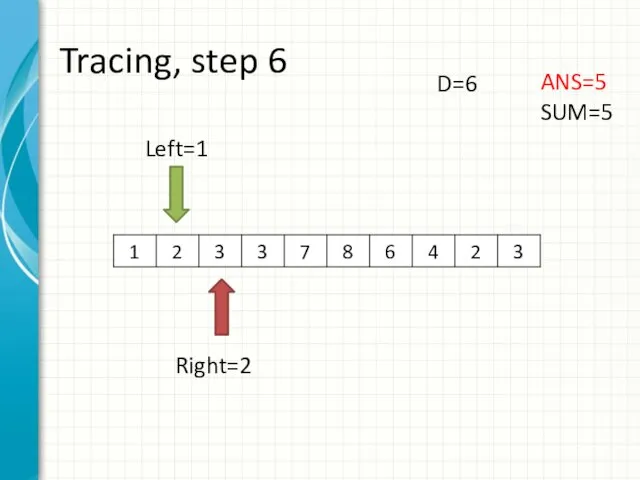
- 14. Tracing, step 6 Left=1 Right=2 ANS=5 SUM=5 D=6
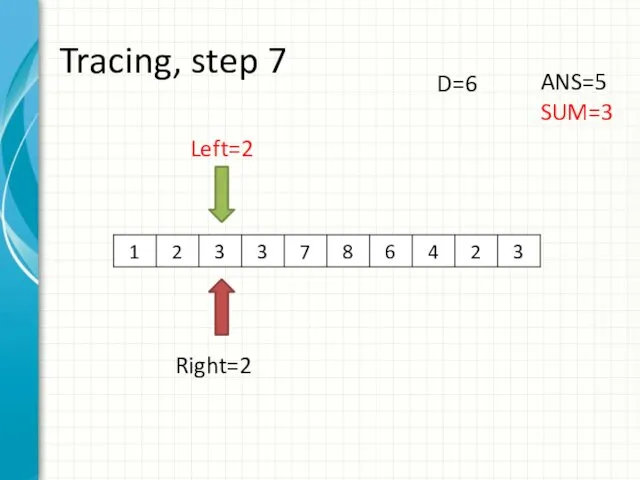
- 15. Tracing, step 7 Left=2 Right=2 ANS=5 SUM=3 D=6
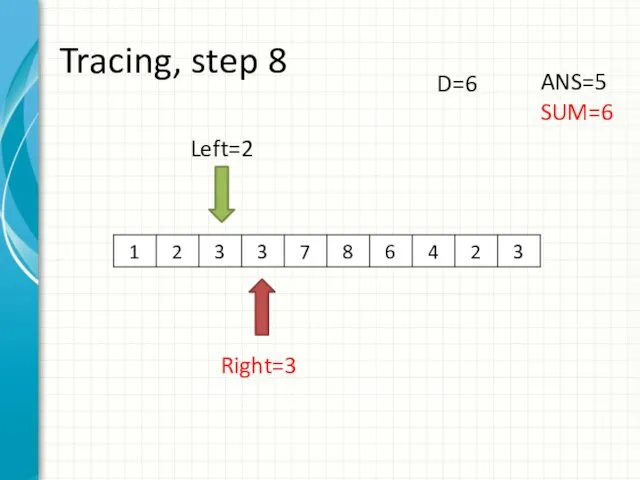
- 16. Tracing, step 8 Left=2 Right=3 ANS=5 SUM=6 D=6
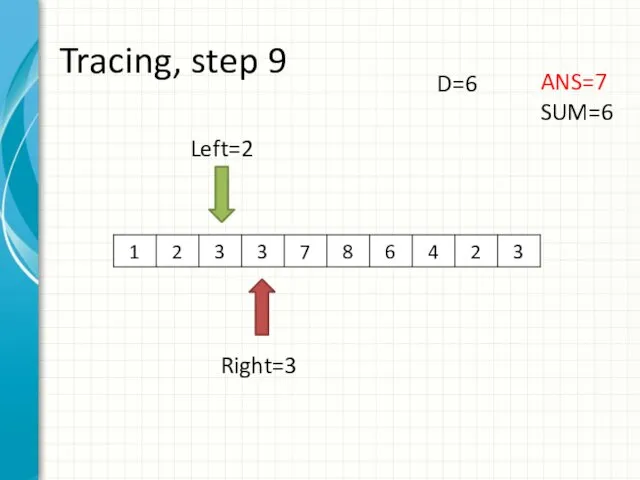
- 17. Tracing, step 9 Left=2 Right=3 ANS=7 SUM=6 D=6
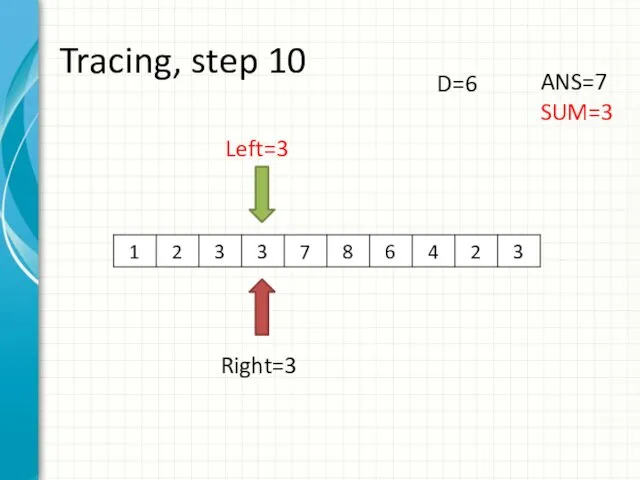
- 18. Tracing, step 10 Left=3 Right=3 ANS=7 SUM=3 D=6
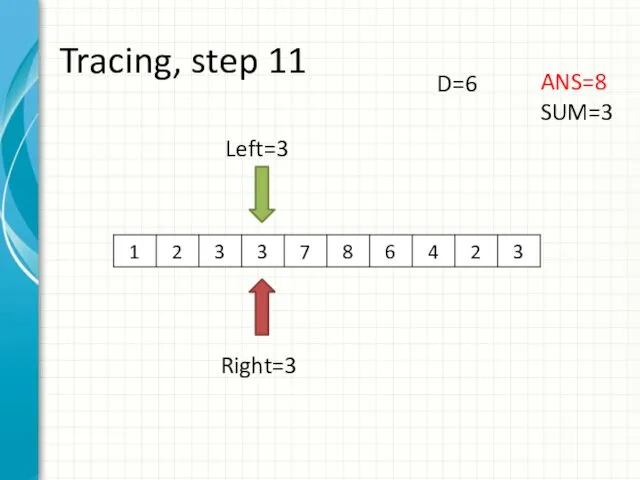
- 19. Tracing, step 11 Left=3 Right=3 ANS=8 SUM=3 D=6
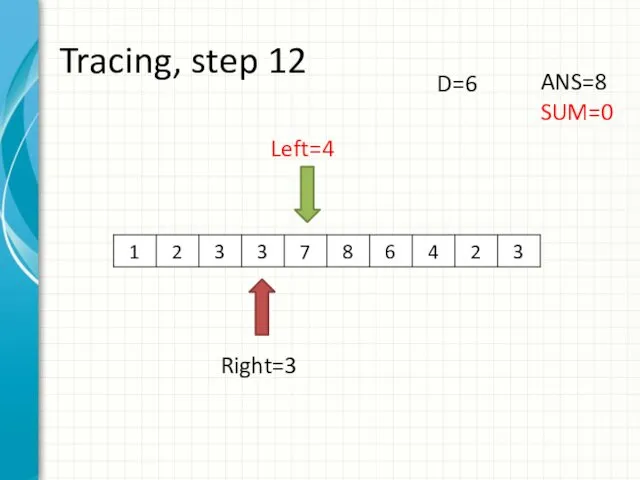
- 20. Tracing, step 12 Left=4 Right=3 ANS=8 SUM=0 D=6
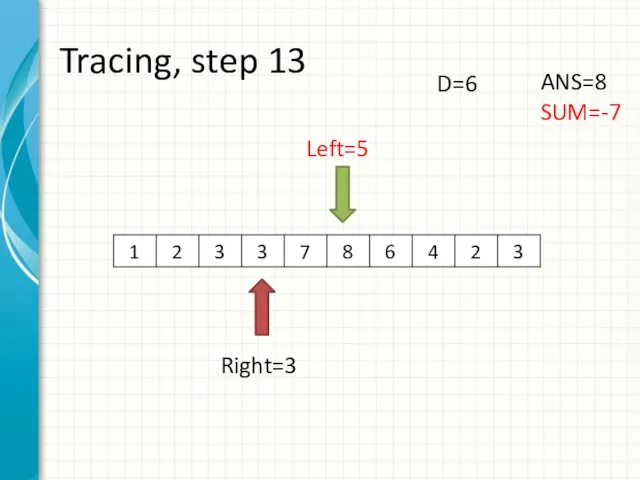
- 21. Tracing, step 13 Left=5 Right=3 ANS=8 SUM=-7 D=6
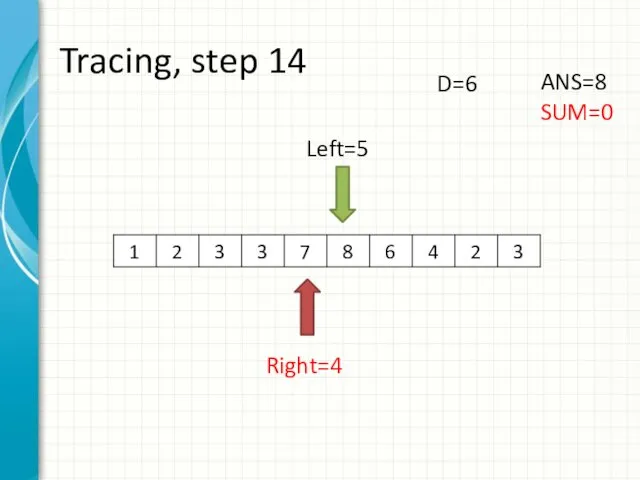
- 22. Tracing, step 14 Left=5 Right=4 ANS=8 SUM=0 D=6
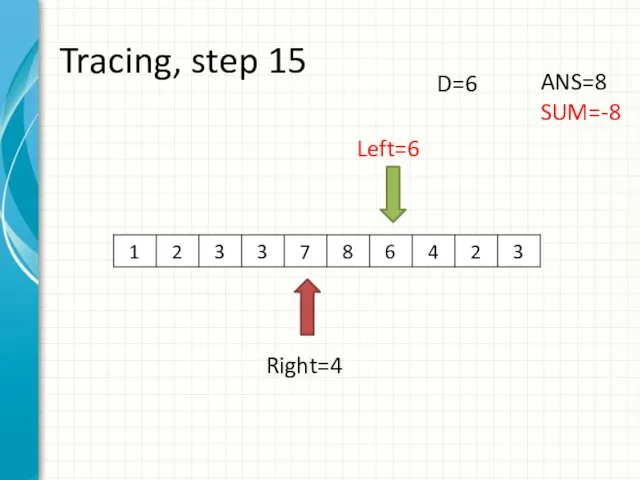
- 23. Tracing, step 15 Left=6 Right=4 ANS=8 SUM=-8 D=6
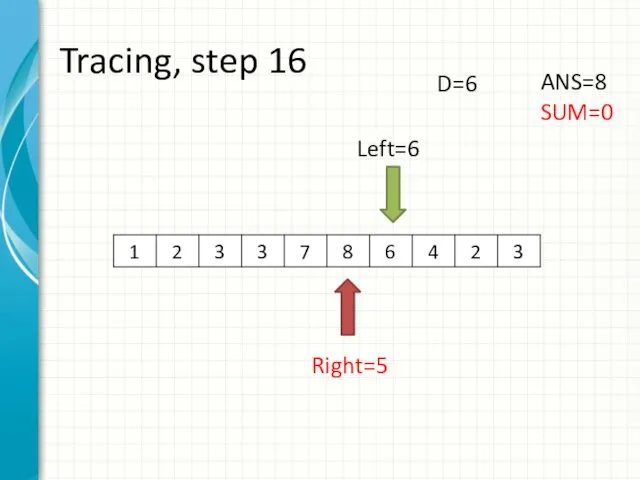
- 24. Tracing, step 16 Left=6 Right=5 ANS=8 SUM=0 D=6
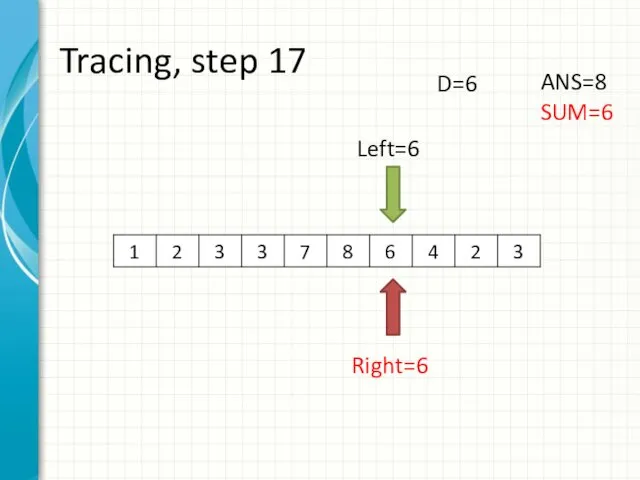
- 25. Tracing, step 17 Left=6 Right=6 ANS=8 SUM=6 D=6
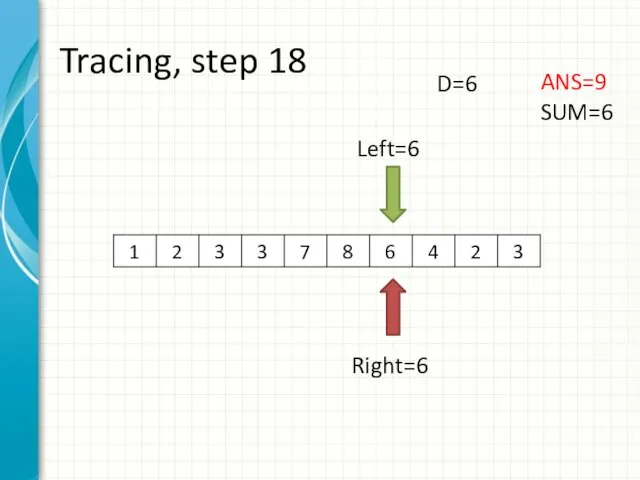
- 26. Tracing, step 18 Left=6 Right=6 ANS=9 SUM=6 D=6
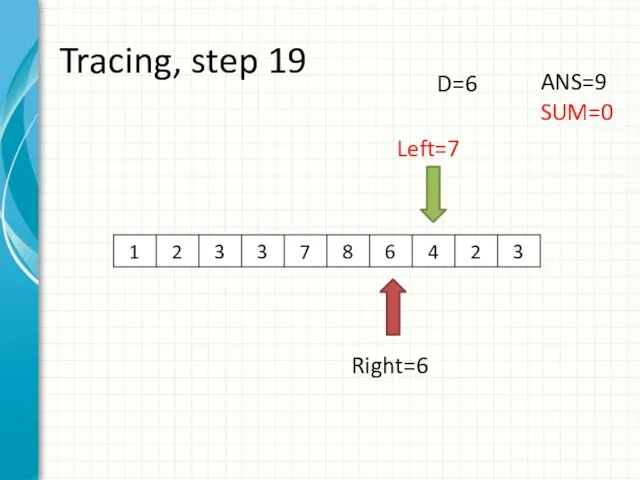
- 27. Tracing, step 19 Left=7 Right=6 ANS=9 SUM=0 D=6
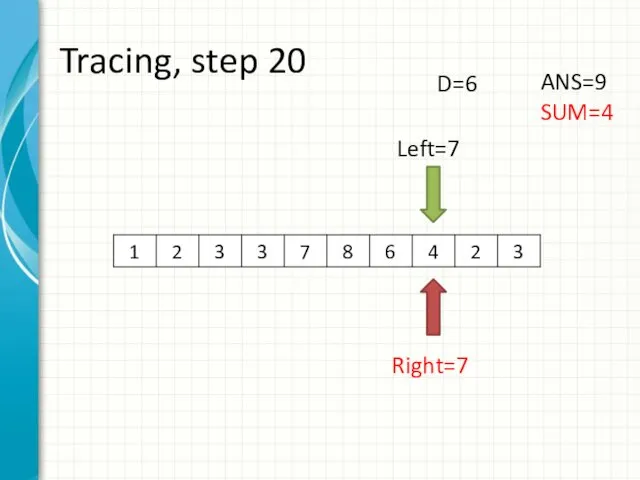
- 28. Tracing, step 20 Left=7 Right=7 ANS=9 SUM=4 D=6
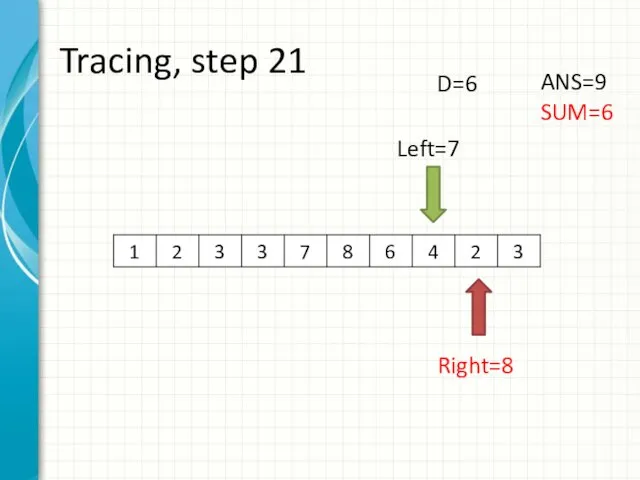
- 29. Tracing, step 21 Left=7 Right=8 ANS=9 SUM=6 D=6
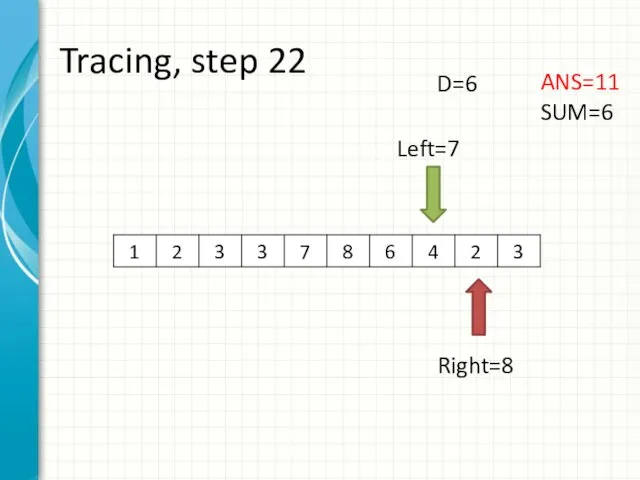
- 30. Tracing, step 22 Left=7 Right=8 ANS=11 SUM=6 D=6
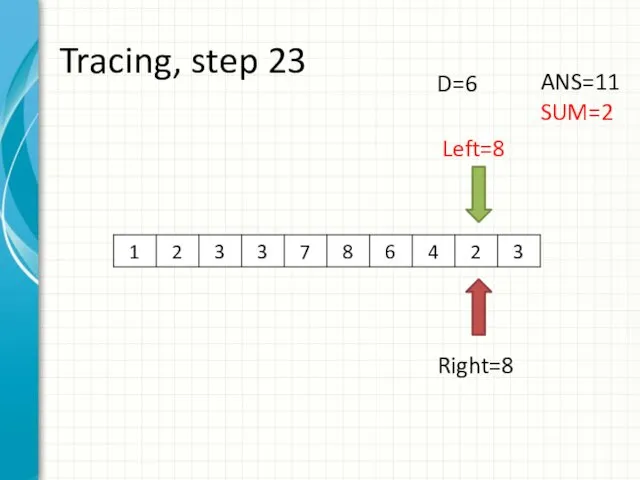
- 31. Tracing, step 23 Left=8 Right=8 ANS=11 SUM=2 D=6
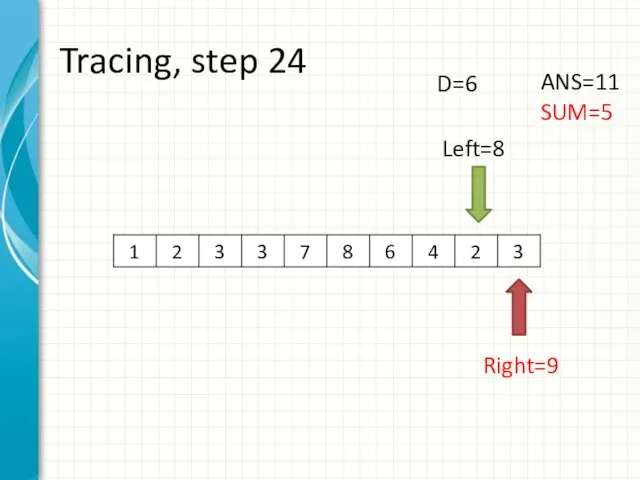
- 32. Tracing, step 24 Left=8 Right=9 ANS=11 SUM=5 D=6
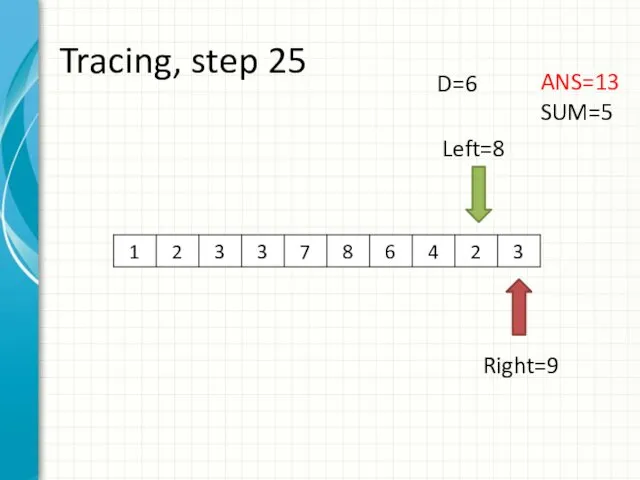
- 33. Tracing, step 25 Left=8 Right=9 ANS=13 SUM=5 D=6
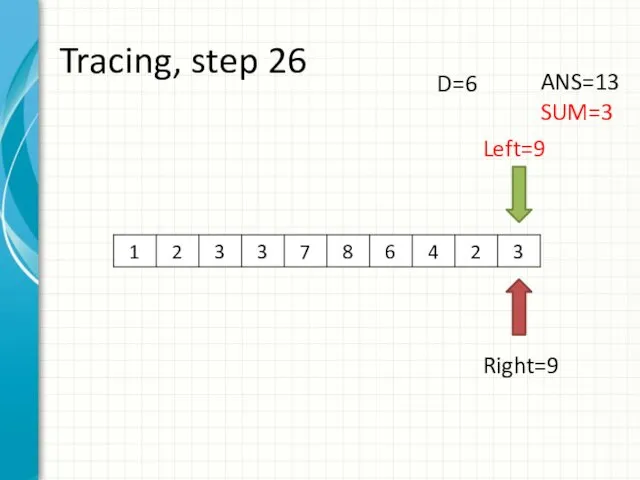
- 34. Tracing, step 26 Left=9 Right=9 ANS=13 SUM=3 D=6
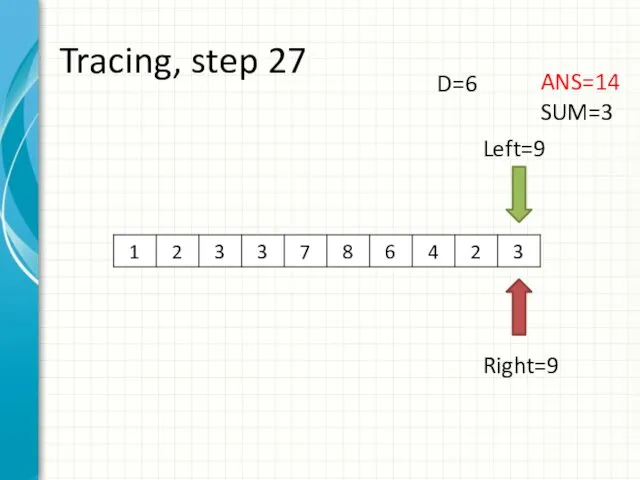
- 35. Tracing, step 27 Left=9 Right=9 ANS=14 SUM=3 D=6
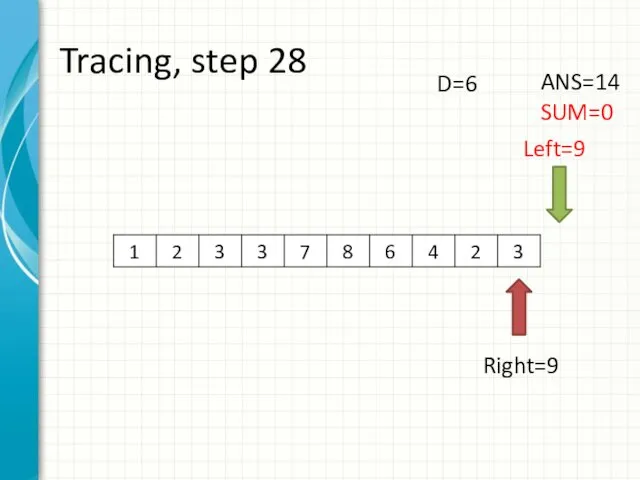
- 36. Tracing, step 28 Left=9 Right=9 ANS=14 SUM=0 D=6
- 37. Other examples There are 2 sorted arrays of integers: A and B. Count pairs (i, j)
- 39. Скачать презентацию


![2. Primitive solution Notice that sum(L, R) = sum(L, R-1)+A[R]](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/20945/slide-3.jpg)

![3. Good solution prefixSum[0] = a[0]; for (int i =](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/20945/slide-5.jpg)


 Позиционные системы счисления
Позиционные системы счисления Локальные сети. Параметры сетей и их стандарты
Локальные сети. Параметры сетей и их стандарты Сбор и подготовка данных
Сбор и подготовка данных Современные накопители информации, используемые в вычислительной технике
Современные накопители информации, используемые в вычислительной технике Использование технологии веб-квест как средство развития познавательных и творческих способностей учащихся
Использование технологии веб-квест как средство развития познавательных и творческих способностей учащихся Блочные алгоритмы. Блочное шифрование. Сравнение блочных и поточных шифров. Предпосылки создания шифра Фейстеля
Блочные алгоритмы. Блочное шифрование. Сравнение блочных и поточных шифров. Предпосылки создания шифра Фейстеля Параллельное программирование. С++. Thread Support Library. Atomic Operations Library
Параллельное программирование. С++. Thread Support Library. Atomic Operations Library Функции в Excel
Функции в Excel Организация и средства информационных технологий обеспечения управленческой деятельности
Организация и средства информационных технологий обеспечения управленческой деятельности Поиск публикаций и показатели деятельности ученого в Web of Science
Поиск публикаций и показатели деятельности ученого в Web of Science Бездротові мережі
Бездротові мережі Занятие 1. Знакомство с программой Adobe Photoshop
Занятие 1. Знакомство с программой Adobe Photoshop Microsoft Visual Studio — линейка продуктов компании Microsoft
Microsoft Visual Studio — линейка продуктов компании Microsoft Операторы цикла
Операторы цикла Понятие об информации. Представление информации. Информационная деятельность человека.
Понятие об информации. Представление информации. Информационная деятельность человека. Автоматизоване створення запитів у базі даних
Автоматизоване створення запитів у базі даних Архітектура операційних систем
Архітектура операційних систем Windows System Programming
Windows System Programming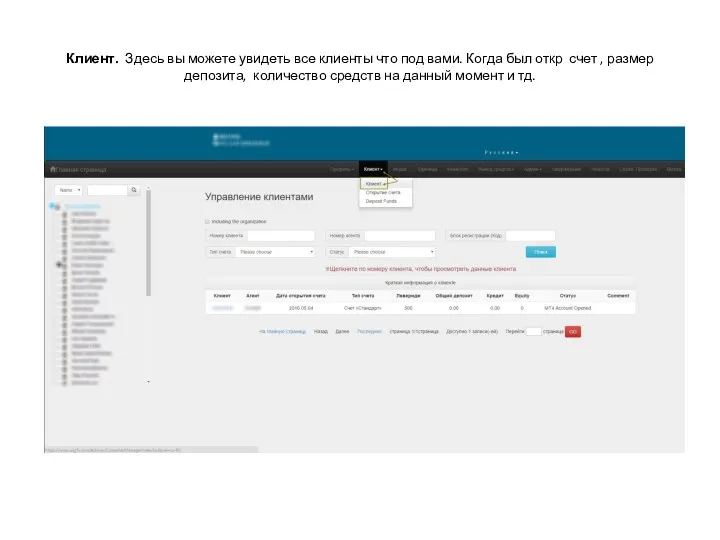 Личный кабинет
Личный кабинет Мир станочника. Аддитивные технологии и 3D-сканирование
Мир станочника. Аддитивные технологии и 3D-сканирование Методы и средства защиты программ от компьютерных вирусов
Методы и средства защиты программ от компьютерных вирусов 46_Yaroslavskaya_Sasha
46_Yaroslavskaya_Sasha Локальные и глобальные сети ЭВМ. Защита информации в сетях. (Тема 6)
Локальные и глобальные сети ЭВМ. Защита информации в сетях. (Тема 6) Godseeker. Игра
Godseeker. Игра Рабочий стол. Управление компьютером с помощью мыши
Рабочий стол. Управление компьютером с помощью мыши Проектирование изделий из листового металла в NX
Проектирование изделий из листового металла в NX Эти люди изменили мир
Эти люди изменили мир Электронные ресурсы для детей и юношества в общедоступных библиотеках: создание и использование
Электронные ресурсы для детей и юношества в общедоступных библиотеках: создание и использование