Содержание
- 2. 1. Векторные и скалярные величины Скалярные (числовыми) величины при выбранной единице измерения вполне характеризуются одним числовым
- 3. 2. Векторы Любой отрезок прямой имеет две концевые точки. Если одна из них принята за начало
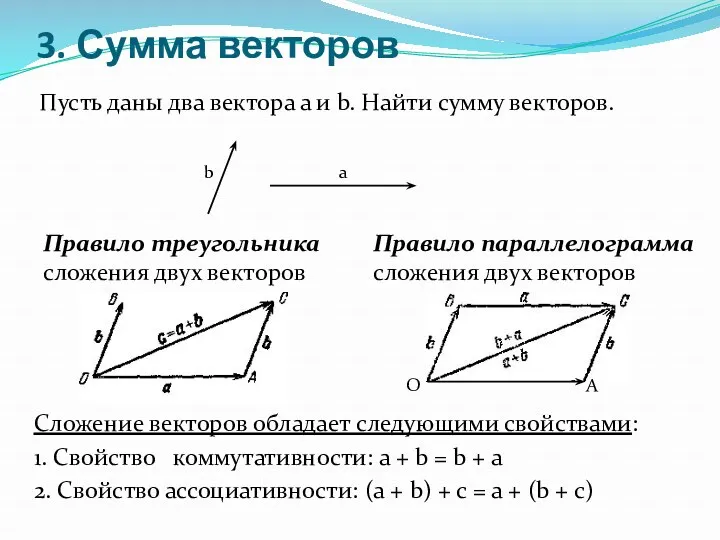
- 4. 3. Сумма векторов Правило треугольника сложения двух векторов Правило параллелограмма сложения двух векторов О А Пусть
- 5. 3. Сумма векторов Если требуется найти сумму трех или большего числа векторов, то применяют так называемое
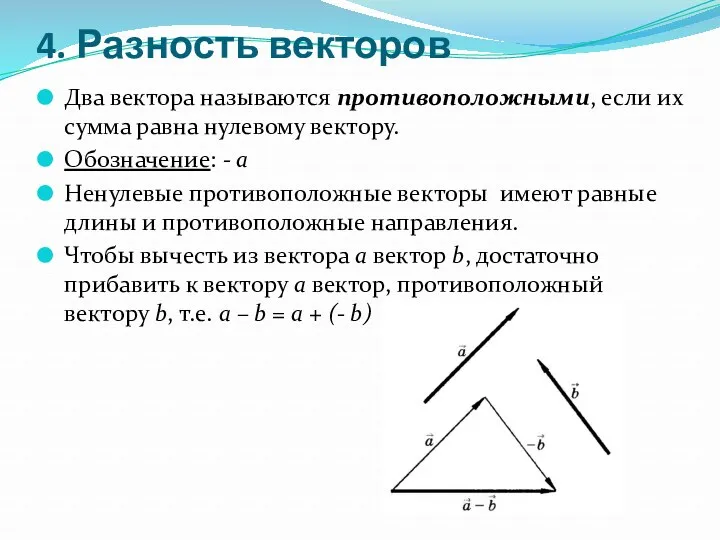
- 6. 4. Разность векторов Два вектора называются противоположными, если их сумма равна нулевому вектору. Обозначение: - а
- 7. 5. Произведение вектора на число Произведением ненулевого вектора а на число m называется вектор, имеющий направление
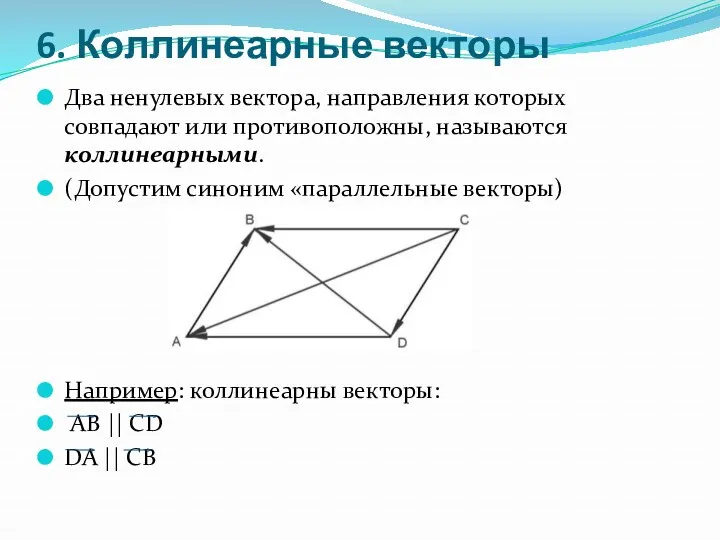
- 8. 6. Коллинеарные векторы Два ненулевых вектора, направления которых совпадают или противоположны, называются коллинеарными. (Допустим синоним «параллельные
- 9. 6. Коллинеарные векторы Теорема (признак коллинеарности). Для того чтобы вектор а был коллинеарен ненулевому вектору b,
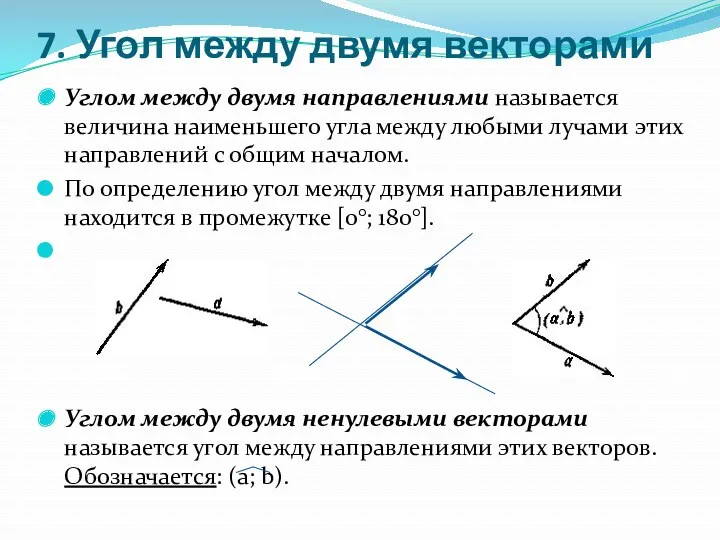
- 10. 7. Угол между двумя векторами Углом между двумя направлениями называется величина наименьшего угла между любыми лучами
- 11. 7. Угол между двумя векторами Если угол между векторами a и b равен 90°, то эти
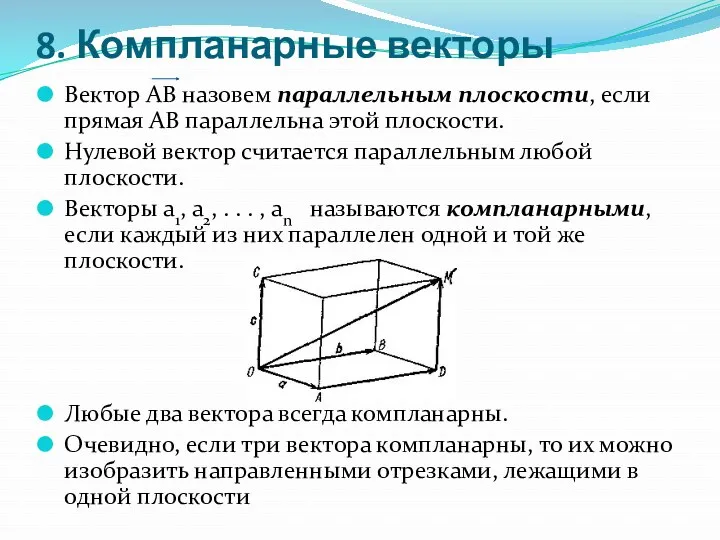
- 12. 8. Компланарные векторы Вектор АВ назовем параллельным плоскости, если прямая АВ параллельна этой плоскости. Нулевой вектор
- 13. 9. Координаты вектора Даны координаты точек в прямоугольной декартовой системе координат: А(хА; уА) и В(хВ; уВ)
- 14. 10. Длина вектора Даны координаты точек в прямоугольной декартовой системе координат: А(хА; уА) и В(хВ; уВ)
- 15. 11. Действия над векторами, заданными своими координатами Пусть даны два вектора, заданные своими координатами: а(х1; y1;
- 16. 11. Действия над векторами, заданными своими координатами Пример: Дано: а = ( 3; 4; 6) и
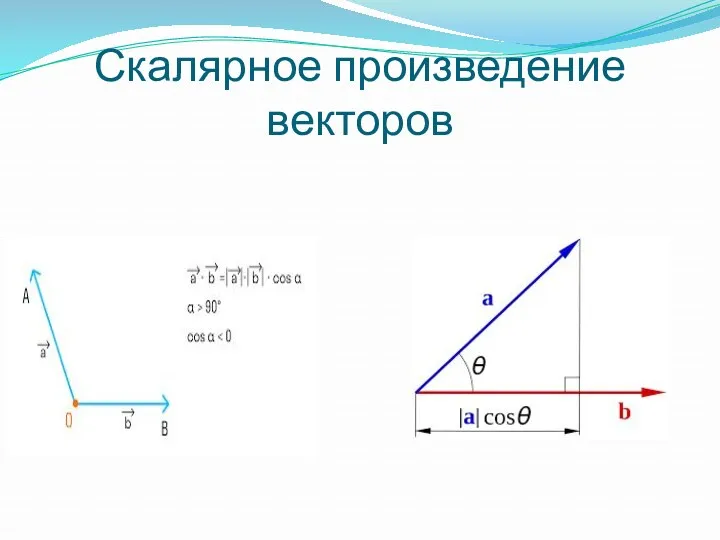
- 17. Скалярное произведение векторов
- 24. Вычислите, какую работу A производит сила (3,4), когда ее точка приложения, двигаясь прямолинейно, перемещается из положения
- 25. Использование скалярного произведения Удобно использовать скалярное произведение векторов для определения углов между прямыми и между прямой
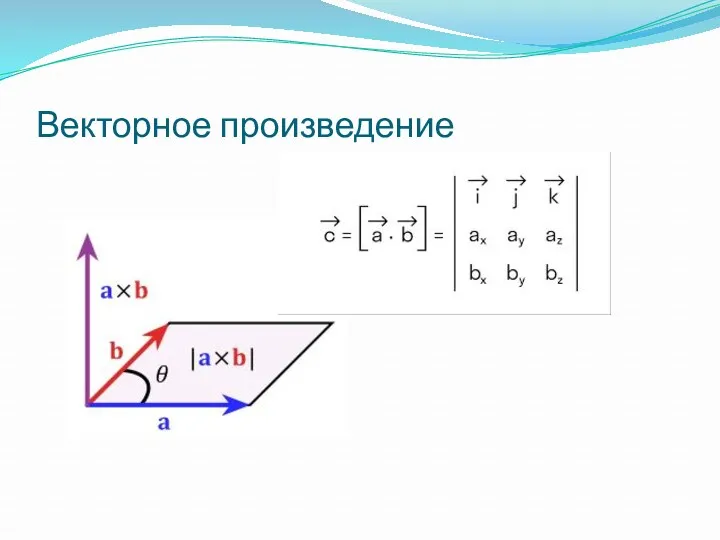
- 26. Векторное произведение
- 30. Скачать презентацию




















 Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени
Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени Ментальная арифметика
Ментальная арифметика Биквадратное уравнение
Биквадратное уравнение Кафе Математики
Кафе Математики Урок математики №3 по теме: Признаки фигур Цвет, форма, размер1 класс программа 2100
Урок математики №3 по теме: Признаки фигур Цвет, форма, размер1 класс программа 2100 Викторина по математике
Викторина по математике Сложение и вычитание десятичных дробей
Сложение и вычитание десятичных дробей Геометрический смысл производной
Геометрический смысл производной Устный счет на уроках математики в 5 - 6 классах
Устный счет на уроках математики в 5 - 6 классах Теория игр и принятие решений
Теория игр и принятие решений Задачи на деление.
Задачи на деление. Решение задач при помощи схематических рисунков (1-2 класс)
Решение задач при помощи схематических рисунков (1-2 класс) Образование чисел второго десятка. 1 класс
Образование чисел второго десятка. 1 класс Число и цифра 6 (1 класс)
Число и цифра 6 (1 класс) Прогрессии или
Прогрессии или Презентация по математике. Устный счет.
Презентация по математике. Устный счет. Одночлен
Одночлен Биквадратные уравнения
Биквадратные уравнения Консультация для учащихся. Алгоритм решения задач.
Консультация для учащихся. Алгоритм решения задач. Типовые классы детерминированных аналитических моделей
Типовые классы детерминированных аналитических моделей Презентация по математике по теме Решение задач на движение 4 класс
Презентация по математике по теме Решение задач на движение 4 класс Дидактический материал по ФЭМП. Занимательная математика
Дидактический материал по ФЭМП. Занимательная математика Бином Ньютона
Бином Ньютона Прямая и обратная пропорциональная зависимости
Прямая и обратная пропорциональная зависимости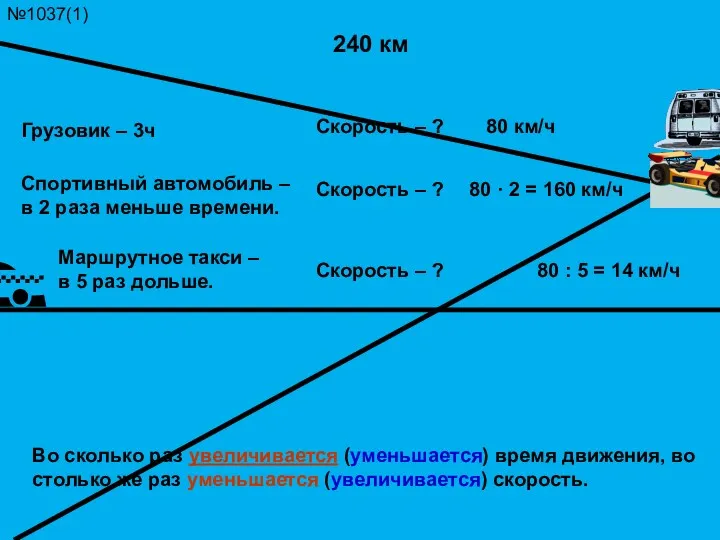 Отношение соответствующих значений. Задачи
Отношение соответствующих значений. Задачи Виды распределения дискретных случайных величин. Закон больших чисел (для детей)
Виды распределения дискретных случайных величин. Закон больших чисел (для детей) Теорема Пифагора
Теорема Пифагора Арифметична прогресiя. Формула n-го члена арифметичної прогресiї
Арифметична прогресiя. Формула n-го члена арифметичної прогресiї