Содержание
- 2. Аксиомы стереометрии и их следствия Взаимное расположение прямых в пространстве Взаимное расположение прямой и плоскости. Параллельность
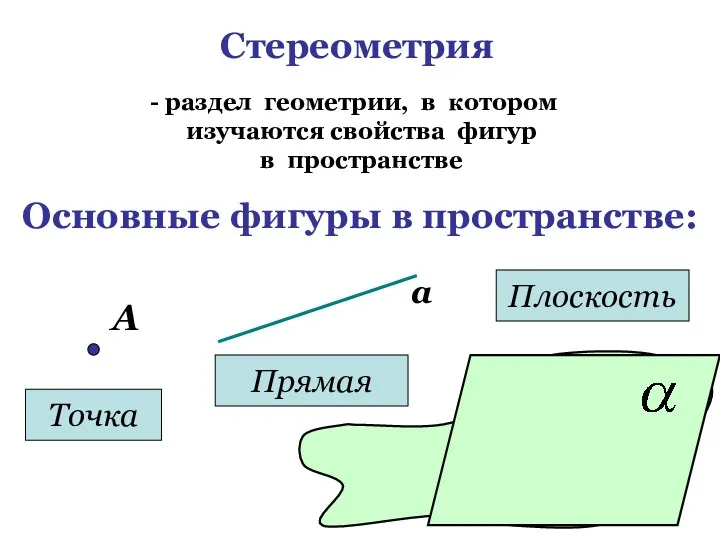
- 4. Стереометрия раздел геометрии, в котором изучаются свойства фигур в пространстве Основные фигуры в пространстве: А Точка
- 5. A, B, C, … a, b, c, … или AВ, BС, CD, …
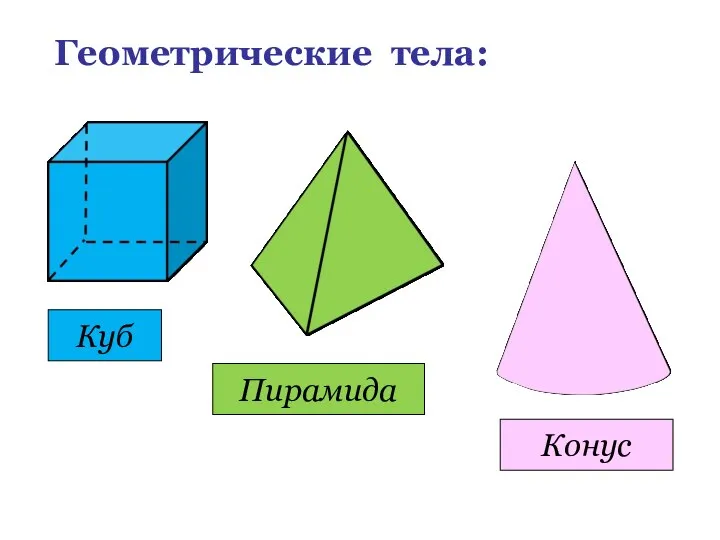
- 6. Геометрические тела: Куб Пирамида Конус
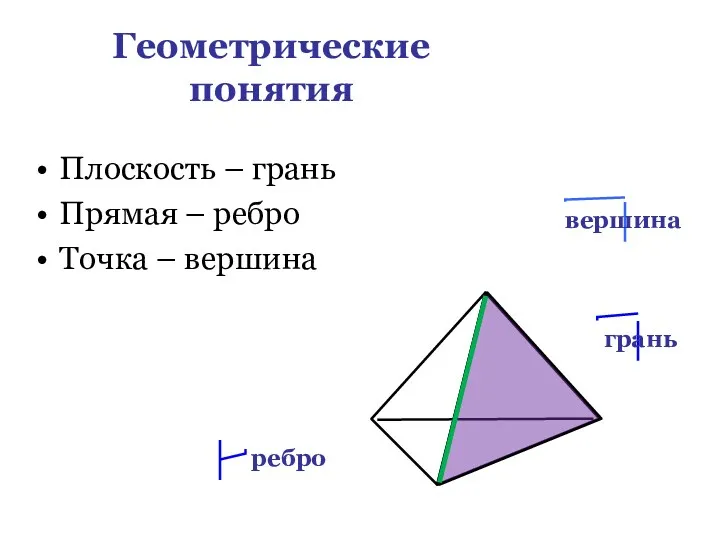
- 7. Геометрические понятия Плоскость – грань Прямая – ребро Точка – вершина вершина грань ребро
- 8. Аксиомы стереометрии и их следствия
- 9. Аксиома (от греч. axíõma – принятие положения) - это утверждение, принимаемое без доказательства Стереометрия широко используется
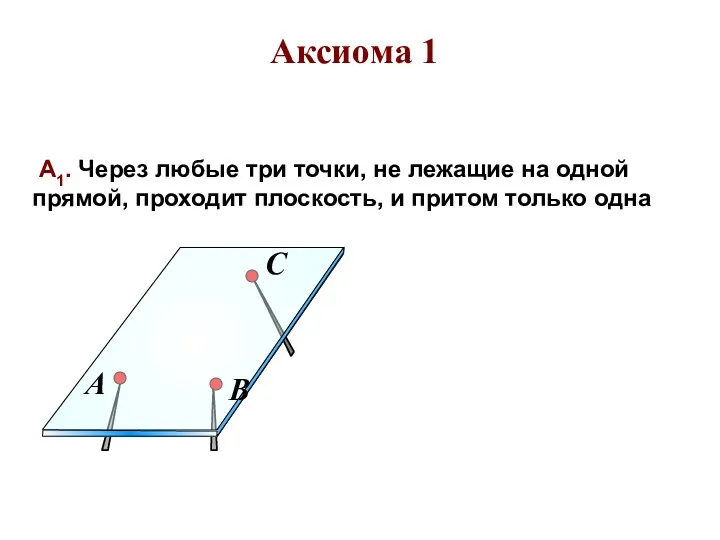
- 10. Аксиома 1 А1. Через любые три точки, не лежащие на одной прямой, проходит плоскость, и притом
- 11. Самый простой пример к аксиоме А1 из повседневной жизни: Табурет с тремя ножками всегда идеально встанет
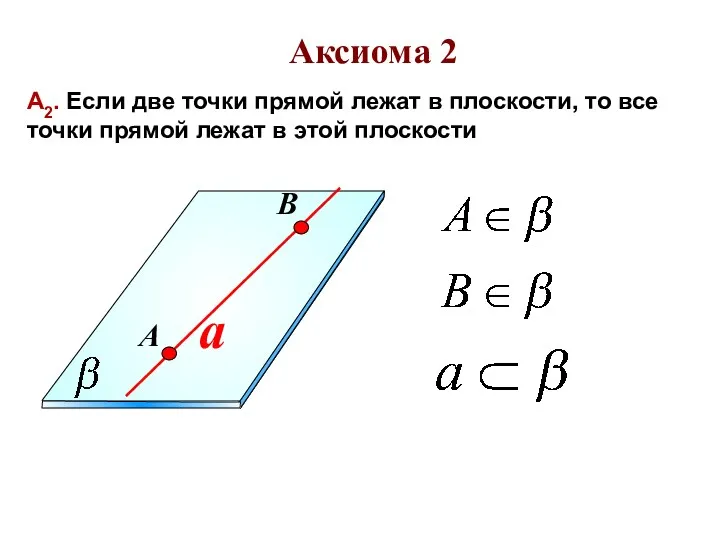
- 12. a А2. Если две точки прямой лежат в плоскости, то все точки прямой лежат в этой
- 13. Свойство, выраженное в аксиоме А2, используется для проверки «ровности» чертежной линейки Линейку прикладывают краем к плоской
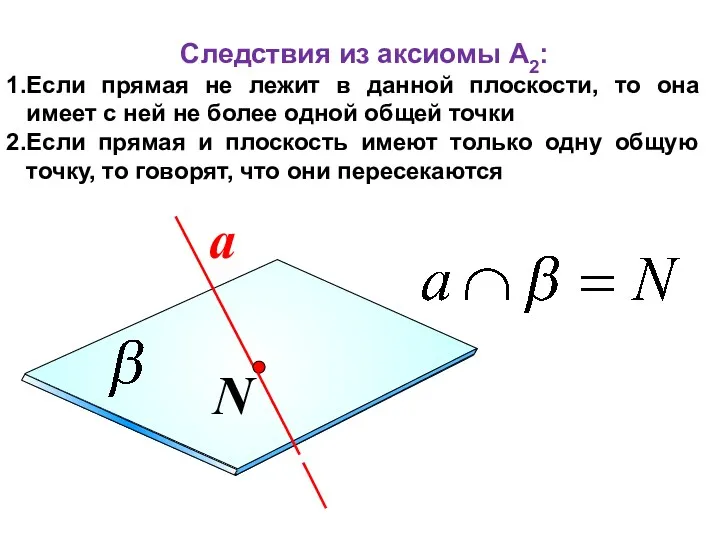
- 14. Следствия из аксиомы А2: Если прямая не лежит в данной плоскости, то она имеет с ней
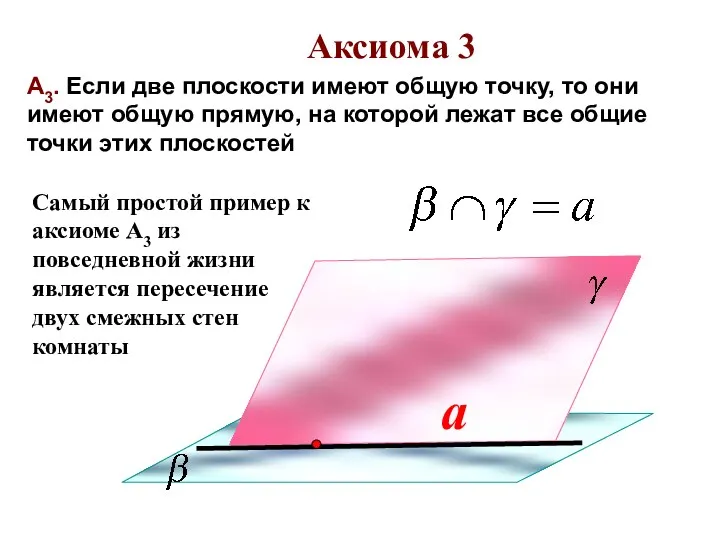
- 15. a А3. Если две плоскости имеют общую точку, то они имеют общую прямую, на которой лежат
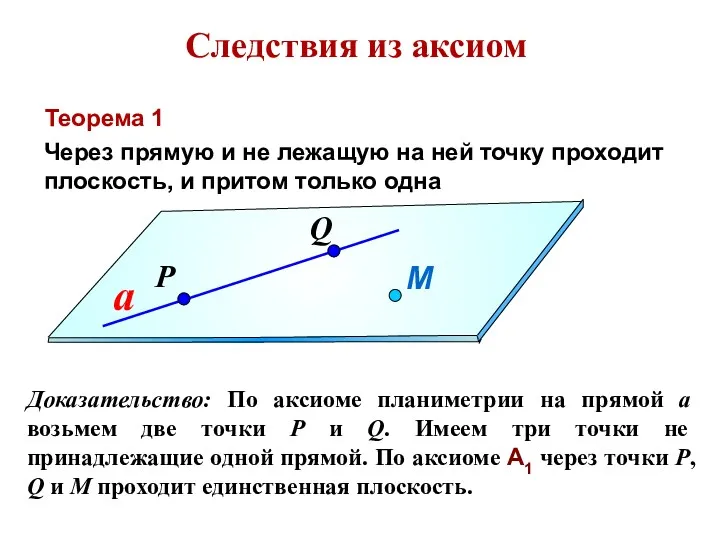
- 16. Следствия из аксиом Теорема 1 Через прямую и не лежащую на ней точку проходит плоскость, и
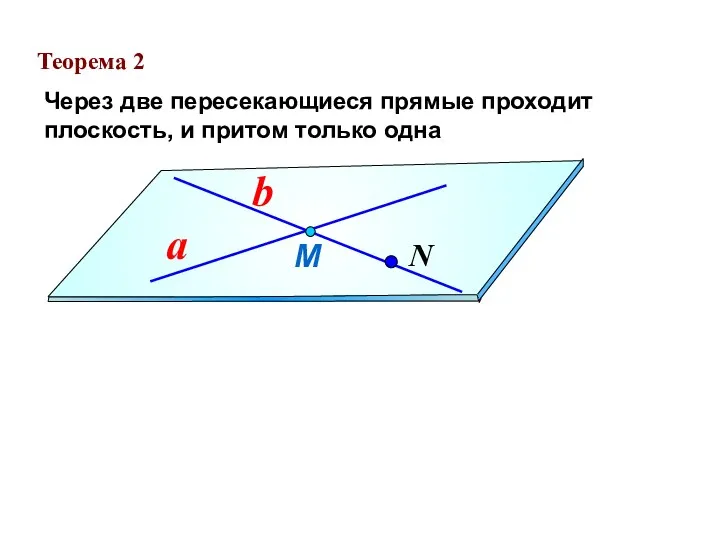
- 17. Теорема 2 Через две пересекающиеся прямые проходит плоскость, и притом только одна М a b N
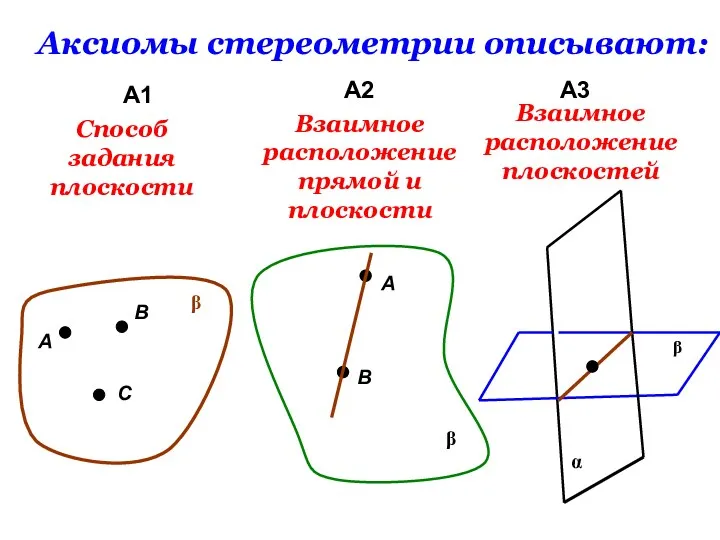
- 18. Аксиомы стереометрии описывают: А1 А2 А3 А В С β Способ задания плоскости β А В
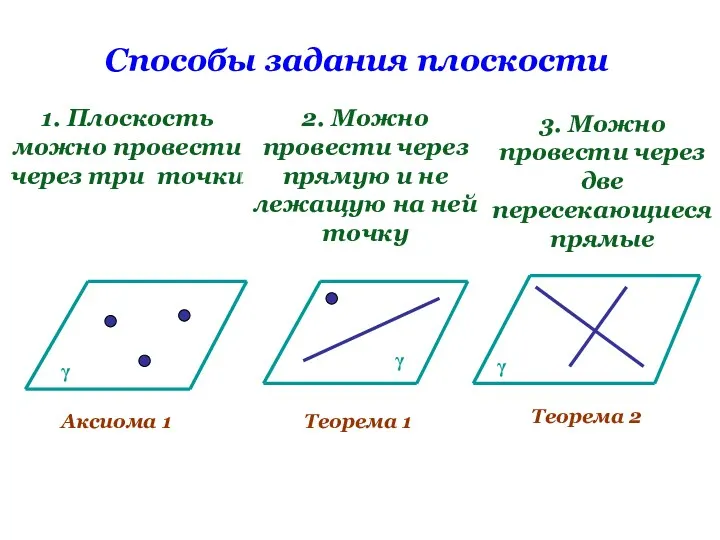
- 19. Способы задания плоскости 1. Плоскость можно провести через три точки 2. Можно провести через прямую и
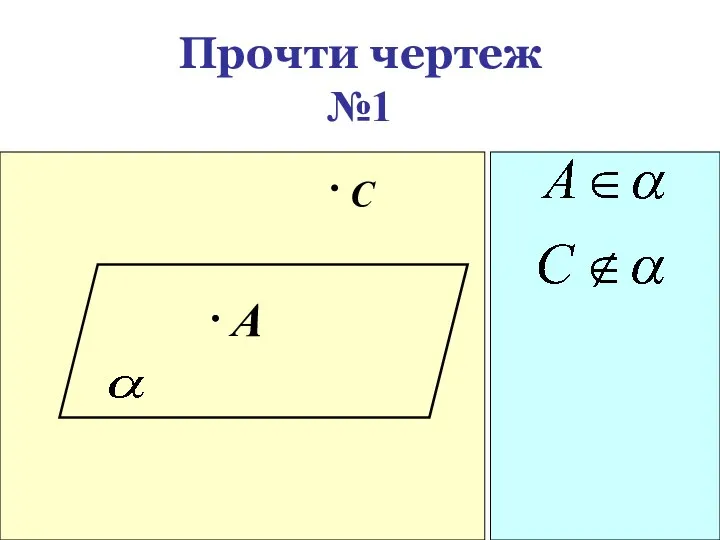
- 20. Прочти чертеж №1 A С
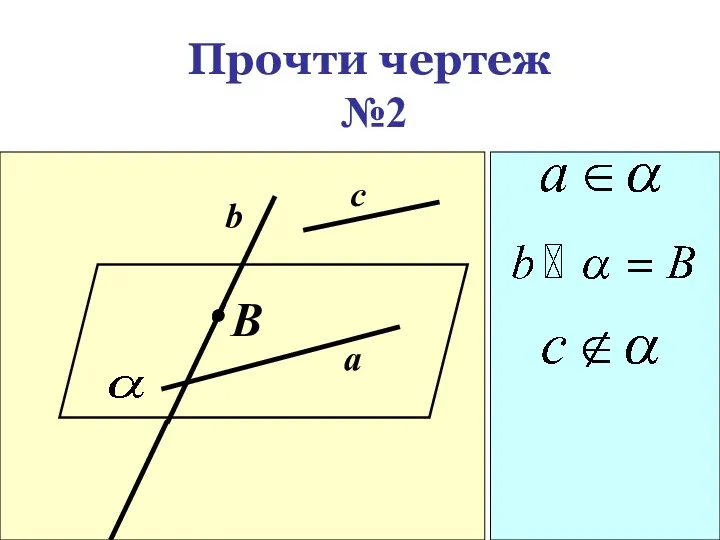
- 21. Прочти чертеж №2 B c b a
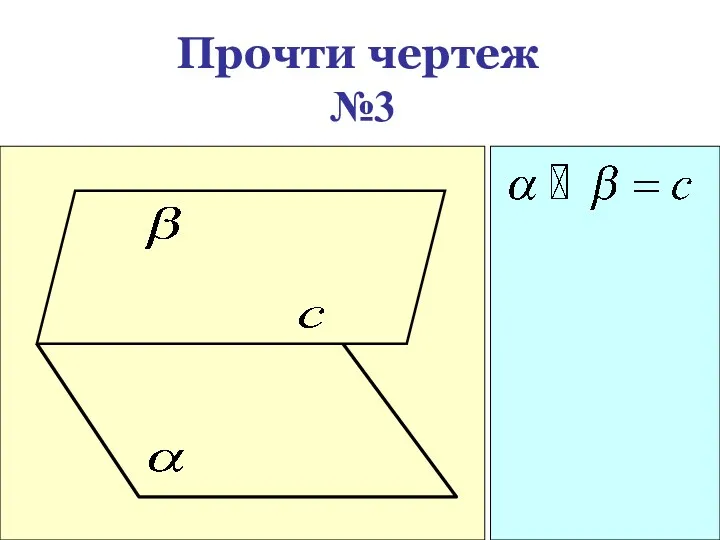
- 22. Прочти чертеж №3
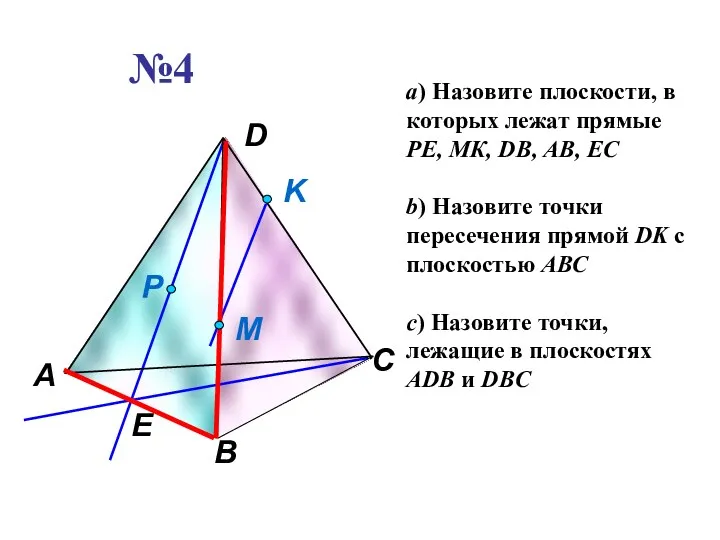
- 23. №4 a) Назовите плоскости, в которых лежат прямые РЕ, МК, DB, AB, EC b) Назовите точки
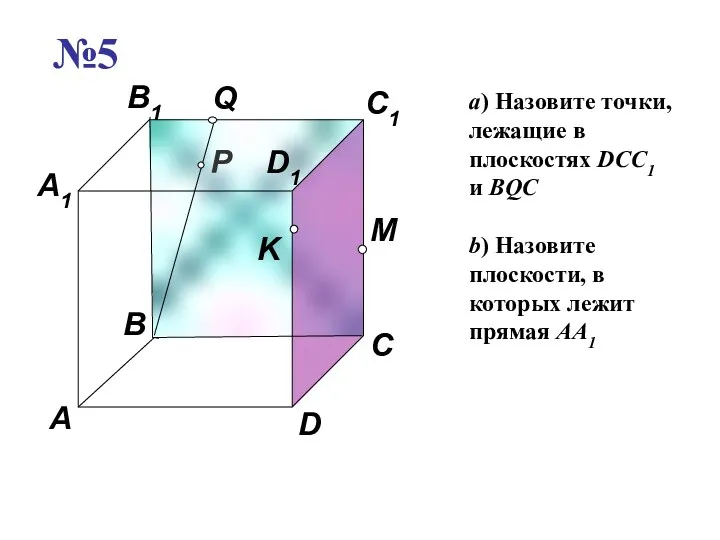
- 24. P A B C D A1 B1 C1 D1 M K Q №5 a) Назовите точки,
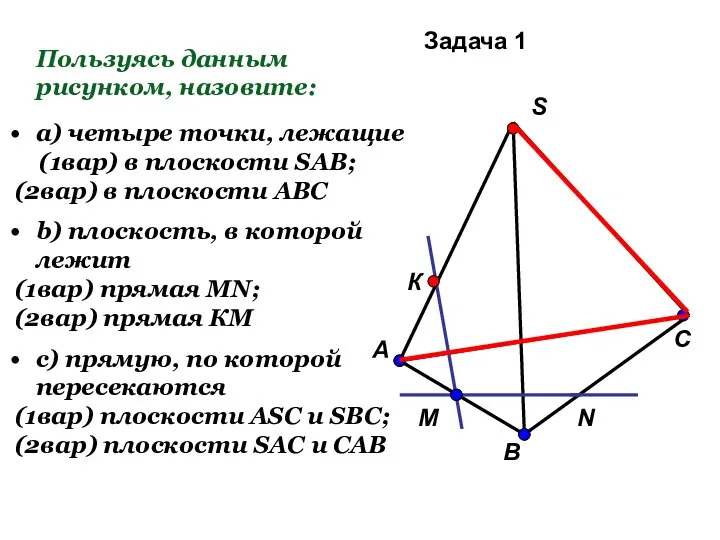
- 25. Пользуясь данным рисунком, назовите: а) четыре точки, лежащие (1вар) в плоскости SAB; (2вар) в плоскости АВС
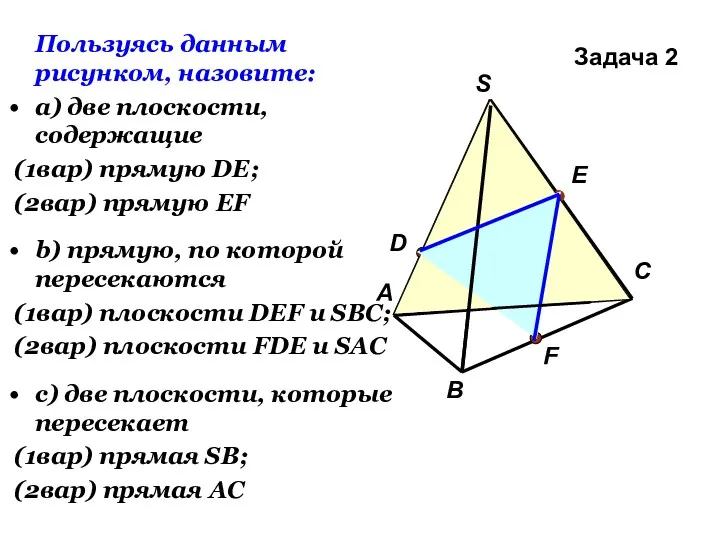
- 26. Пользуясь данным рисунком, назовите: а) две плоскости, содержащие (1вар) прямую DE; (2вар) прямую EF b) прямую,
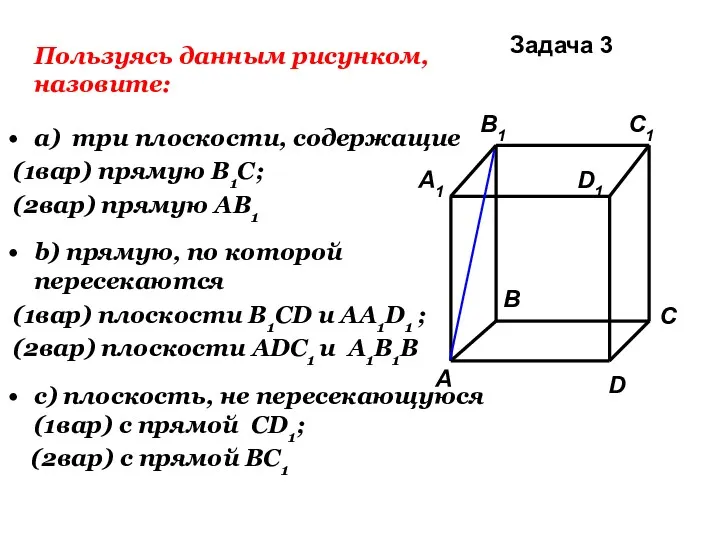
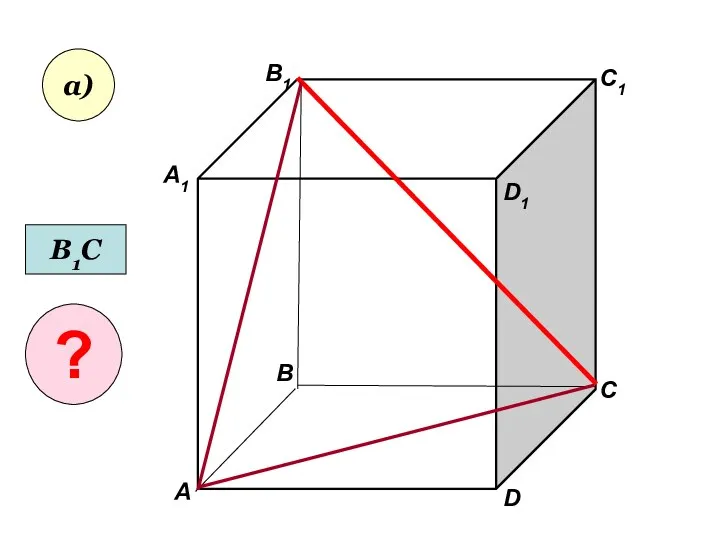
- 27. Пользуясь данным рисунком, назовите: а) три плоскости, содержащие (1вар) прямую В1С; (2вар) прямую АВ1 b) прямую,
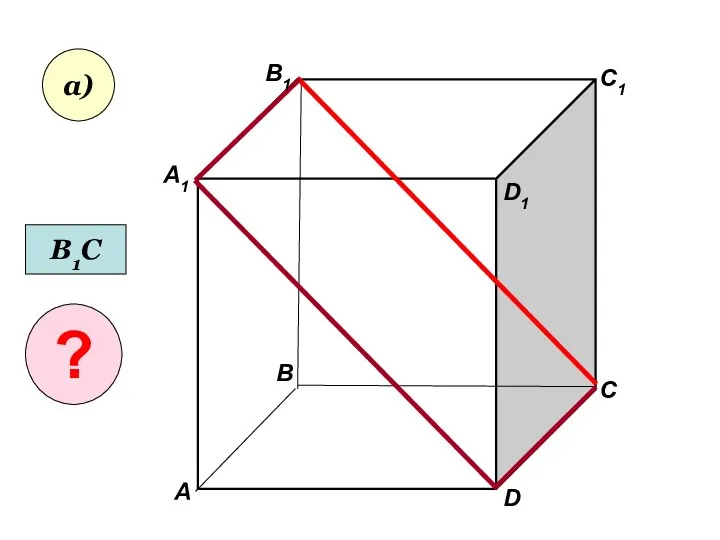
- 28. А А1 В В1 С D1 D C1 а) В1С ?
- 29. А А1 В В1 С D1 D C1 а) В1С ?
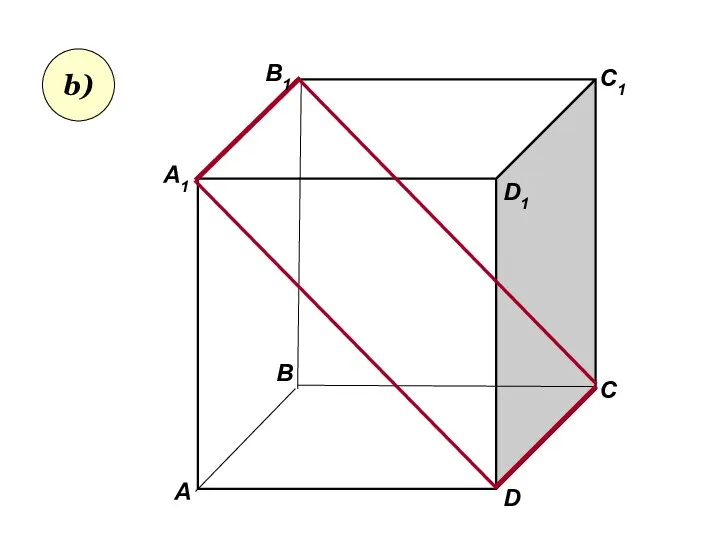
- 30. А А1 В В1 С D1 D C1 b)
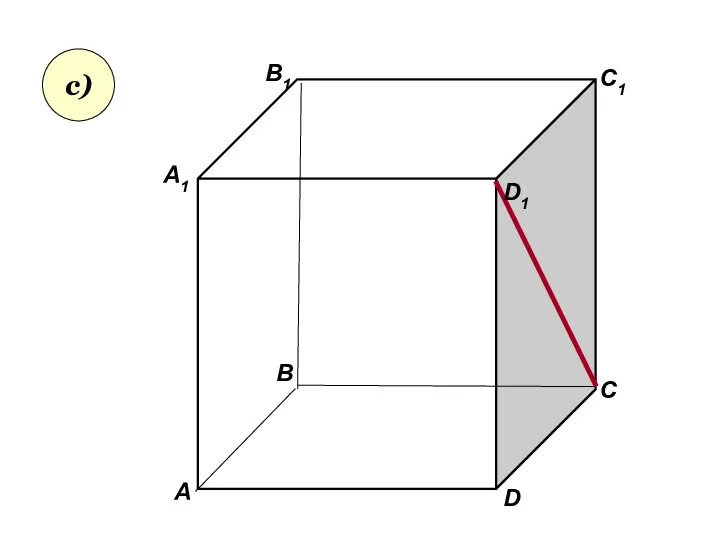
- 31. А А1 В В1 С D1 D C1 с)
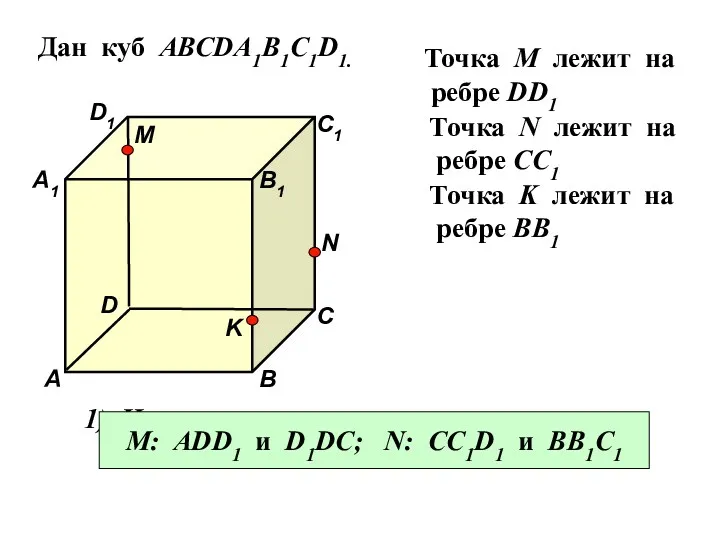
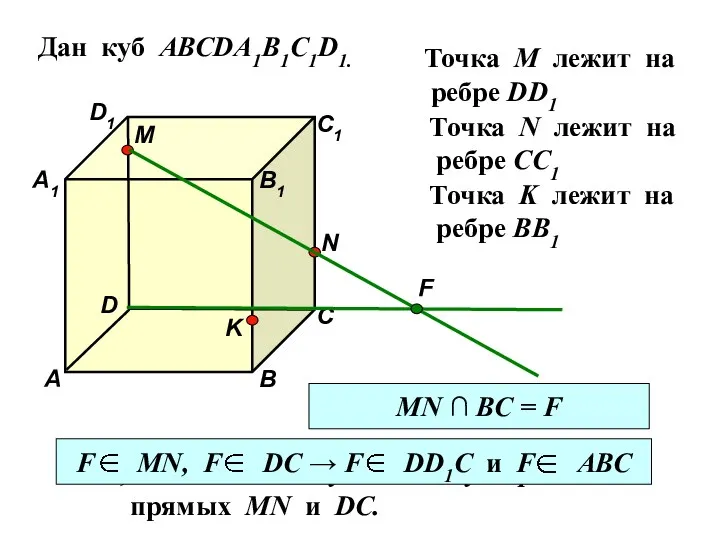
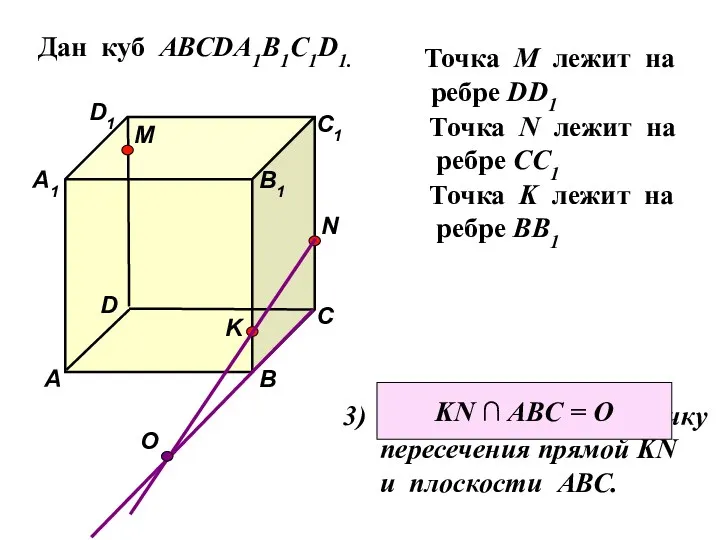
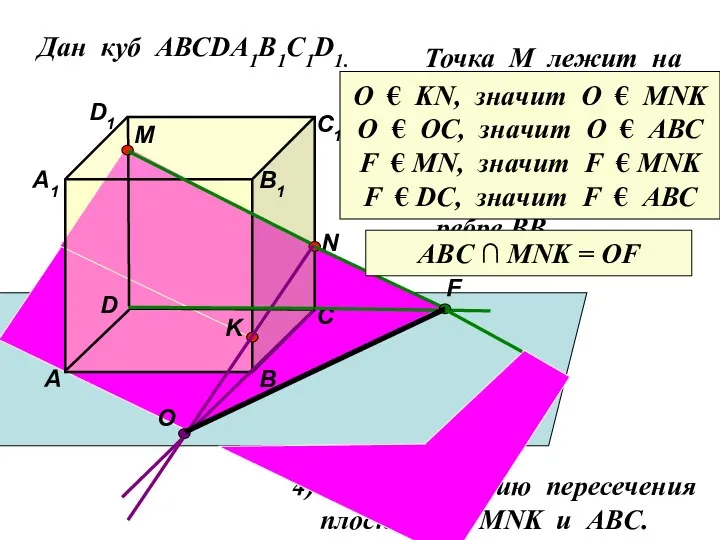
- 32. Дан куб АВСDA1B1C1D1. Точка М лежит на ребре DD1 Точка N лежит на ребре CC1 Точка
- 33. Дан куб АВСDA1B1C1D1. D1 D С1 С В1 В А1 А M Точка М лежит на
- 34. Дан куб АВСDA1B1C1D1. D1 D С1 С В1 В А1 А M Точка М лежит на
- 35. Дан куб АВСDA1B1C1D1. D1 D С1 С В1 В А1 А M Точка М лежит на
- 36. Взаимное расположение прямых в пространстве
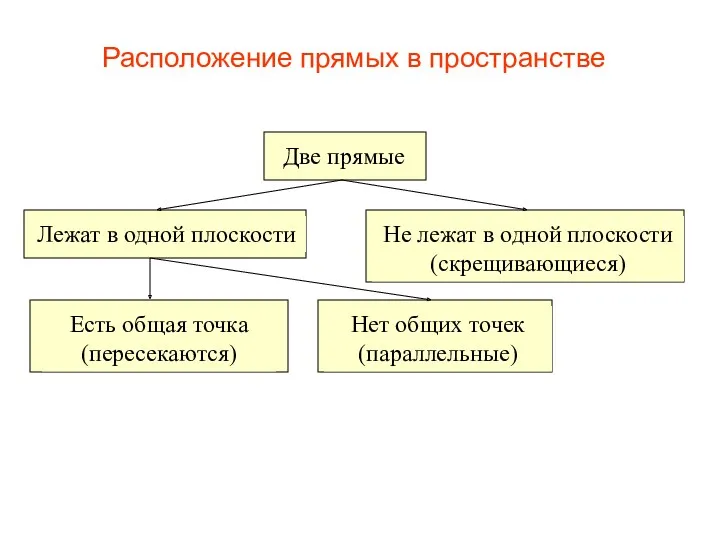
- 37. Две прямые Лежат в одной плоскости Не лежат в одной плоскости (скрещивающиеся) Есть общая точка (пересекаются)
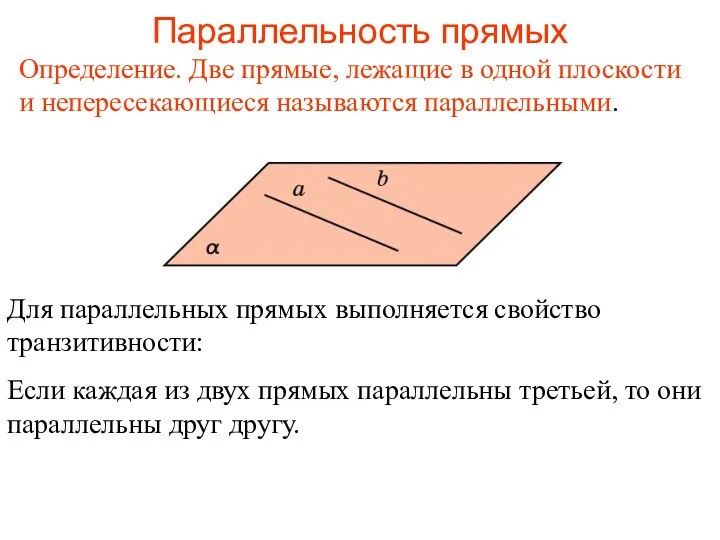
- 38. Определение. Две прямые, лежащие в одной плоскости и непересекающиеся называются параллельными. Параллельность прямых Для параллельных прямых
- 39. Ответ: нет. Всегда ли в пространстве две непересекающиеся прямые параллельны? Упражнение 1
- 40. Ответ: 1. Сколько можно провести плоскостей через две параллельные прямые? Упражнение 2
- 41. Ответ: нет. На плоскости если прямая пересекает одну из параллельных прямых, то она обязательно пересекает и
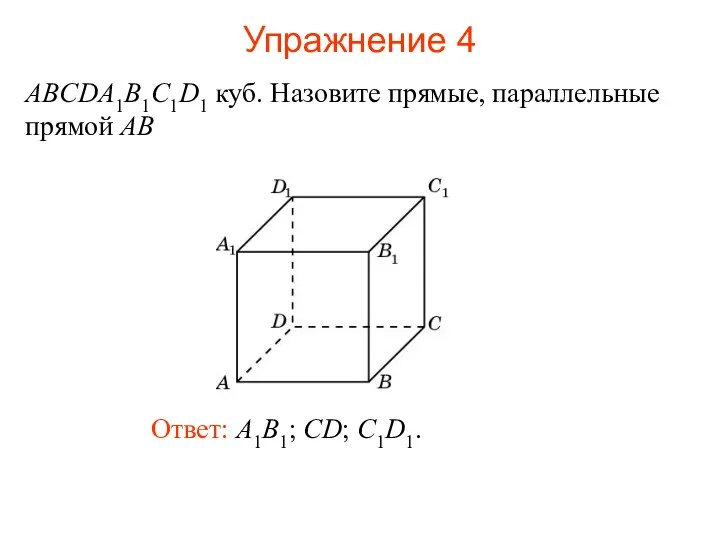
- 42. Ответ: A1B1; CD; C1D1. ABCDA1B1C1D1 куб. Назовите прямые, параллельные прямой АВ Упражнение 4
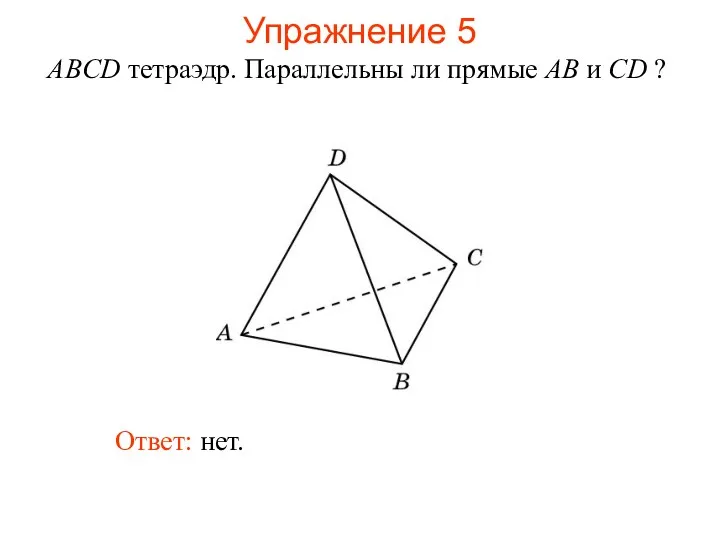
- 43. ABCD тетраэдр. Параллельны ли прямые AB и CD ? Ответ: нет. Упражнение 5
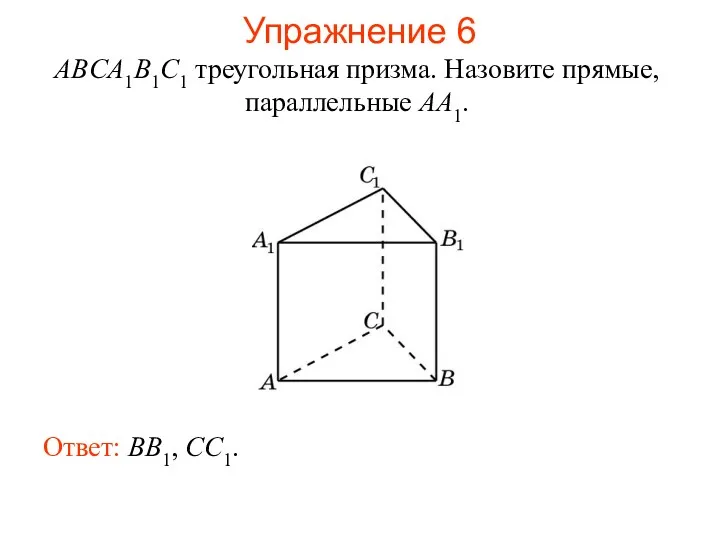
- 44. Ответ: BB1, CC1. Упражнение 6 ABCA1B1C1 треугольная призма. Назовите прямые, параллельные AA1.
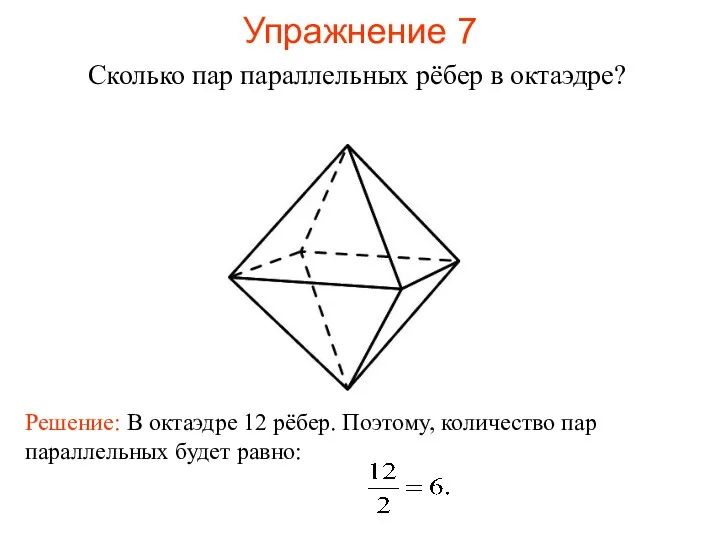
- 45. Сколько пар параллельных рёбер в октаэдре? Упражнение 7
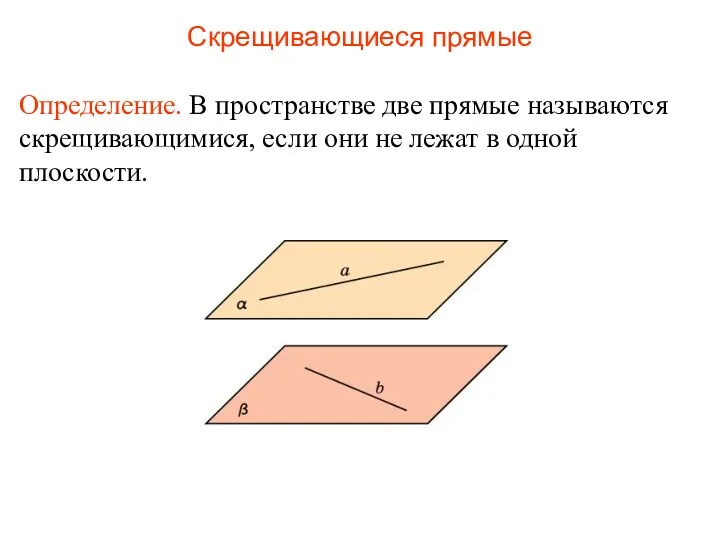
- 46. Определение. В пространстве две прямые называются скрещивающимися, если они не лежат в одной плоскости. Скрещивающиеся прямые
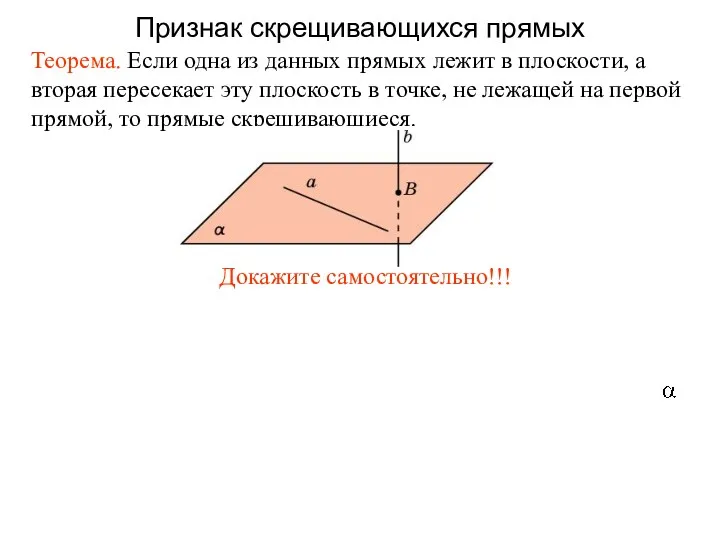
- 47. Теорема. Если одна из данных прямых лежит в плоскости, а вторая пересекает эту плоскость в точке,
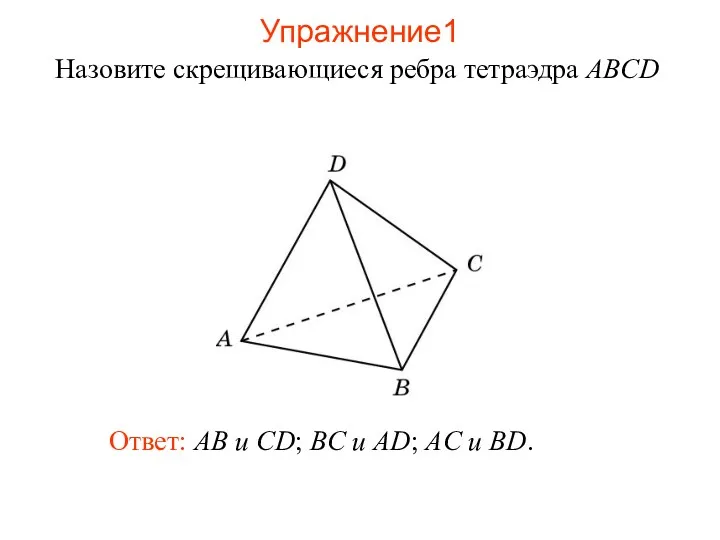
- 48. Назовите скрещивающиеся ребра тетраэдра ABCD Ответ: AB и CD; BC и AD; AC и BD. Упражнение1
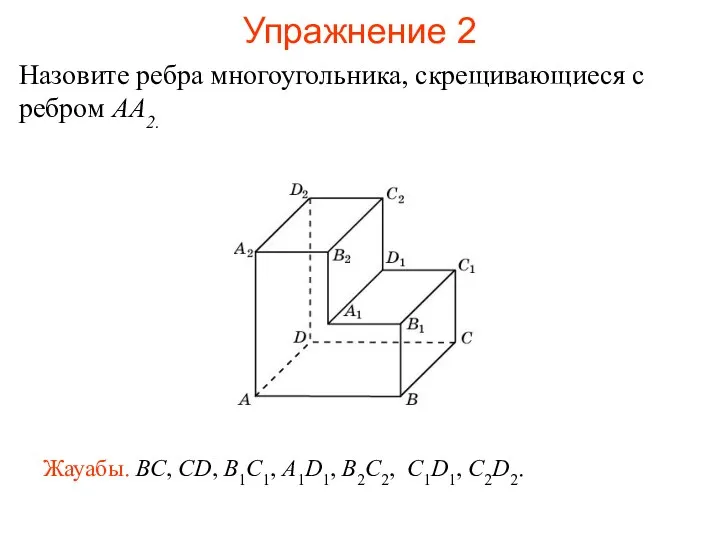
- 49. Назовите ребра многоугольника, скрещивающиеся с ребром AA2. Жауабы. BC, CD, B1C1, A1D1, B2C2, C1D1, C2D2. Упражнение
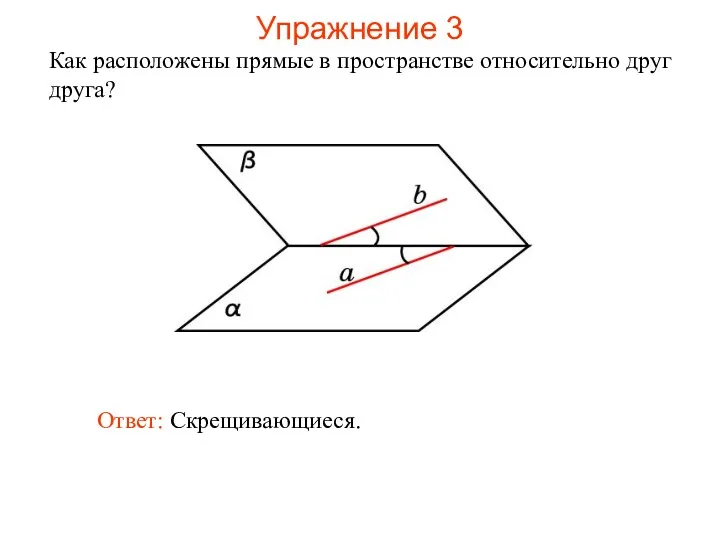
- 50. Ответ: Скрещивающиеся. Как расположены прямые в пространстве относительно друг друга? Упражнение 3
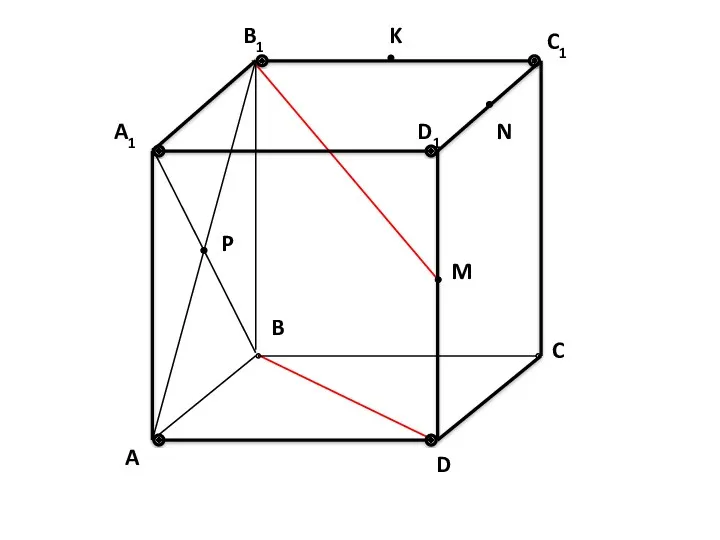
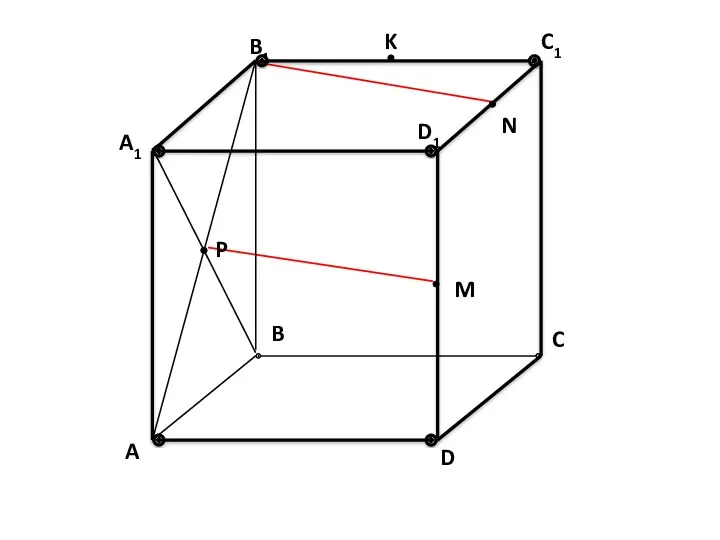
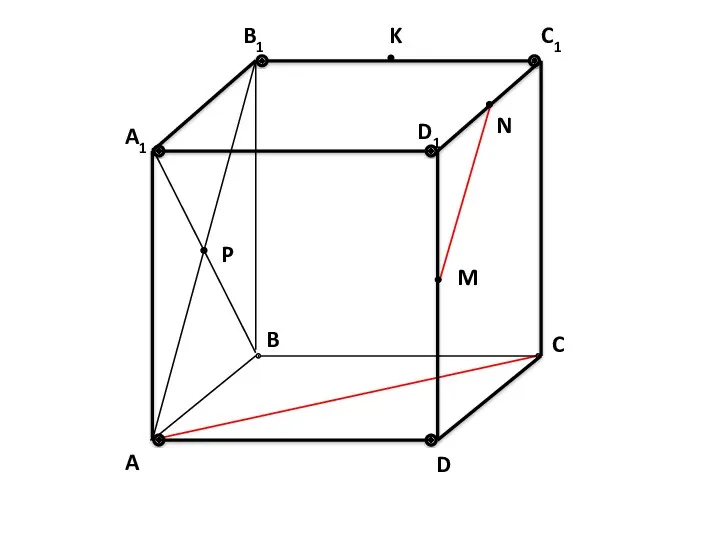
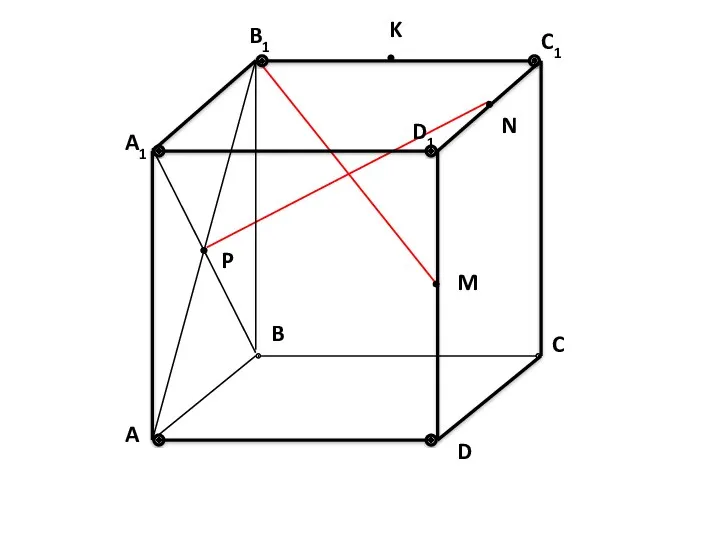
- 51. A B1 A1 P C B D D1 M N K C1 Дано: ABCDA1B1C1D1 – КУБ.
- 52. A B1 A1 P C B D D1 M N K C1 Определите взаимное расположение прямых.
- 53. A B1 A1 P C B D D1 M N K C1
- 54. A B1 A1 P C B D D1 M N K C1
- 55. A B1 A1 P C B D D1 M N K C1
- 56. A B1 A1 P C B D D1 M N K C1
- 57. Проверь себя Скрещиваются Пересекаются Параллельны Скрещиваются Пересекаются
- 58. Взаимное расположение прямой и плоскости
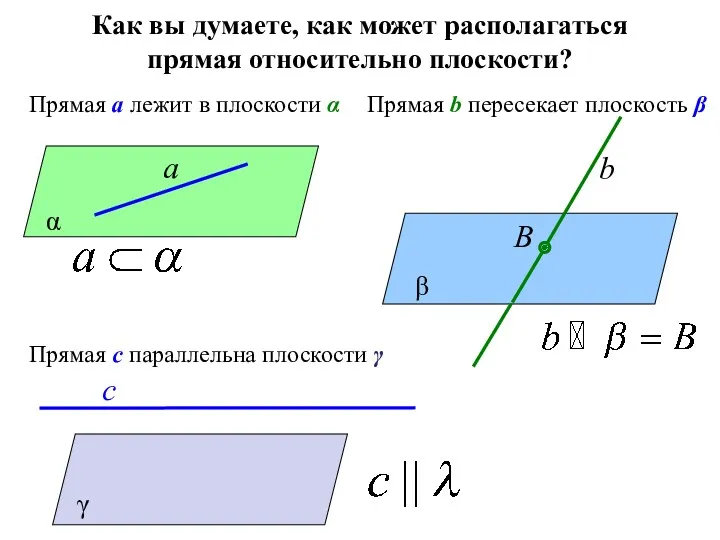
- 59. Как вы думаете, как может располагаться прямая относительно плоскости? α а β b B γ c
- 60. γ c Прямая c параллельна плоскости γ Прямая и плоскость называются параллельными, если они не пересекаются.
- 61. Прямая называется перпендикулярной плоскости, если она перпендикулярна любой прямой, лежащей в этой плоскости.
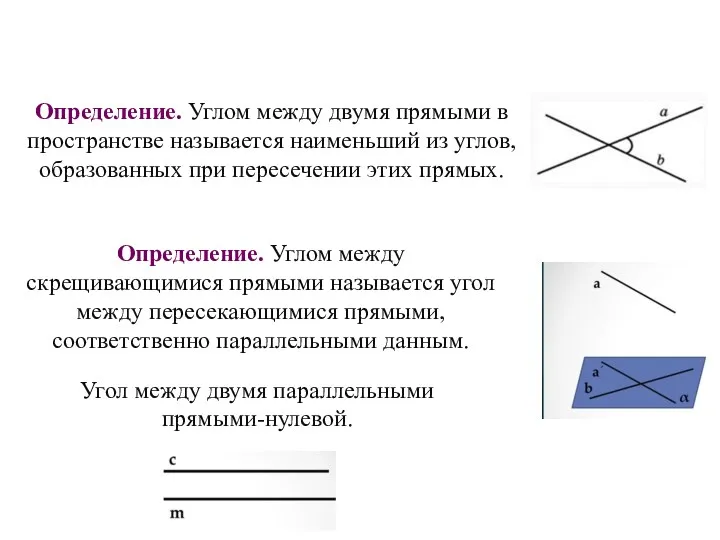
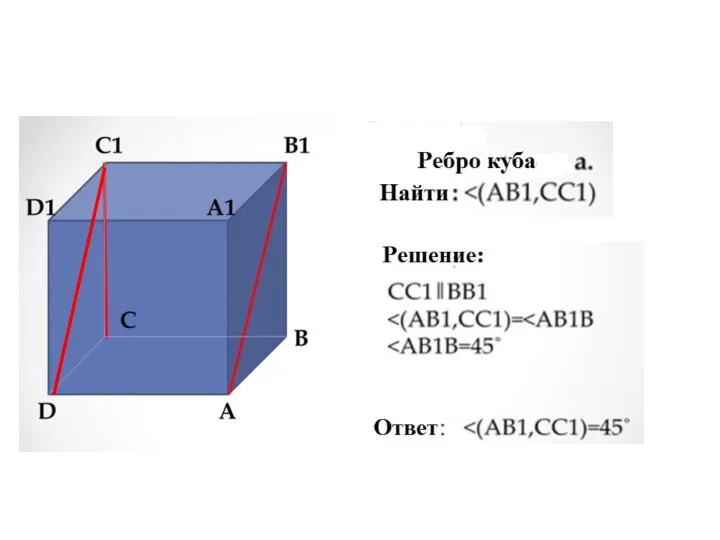
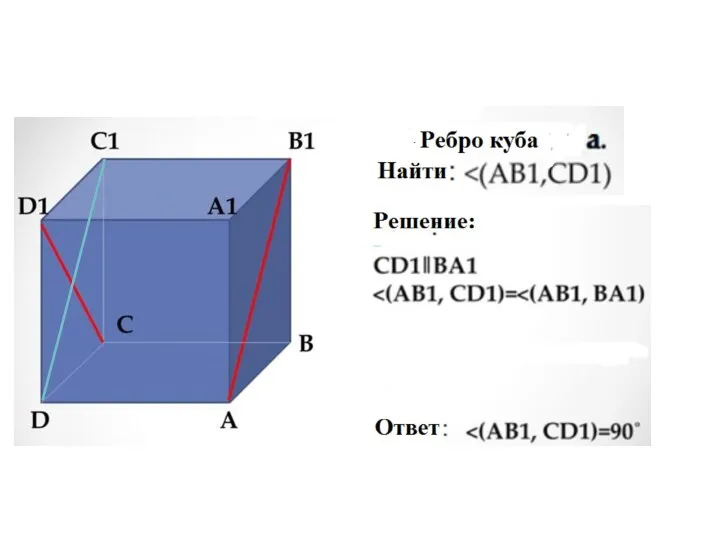
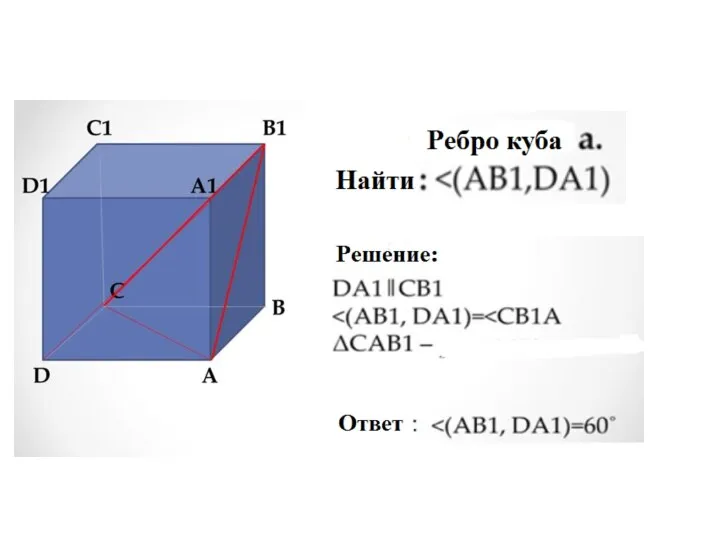
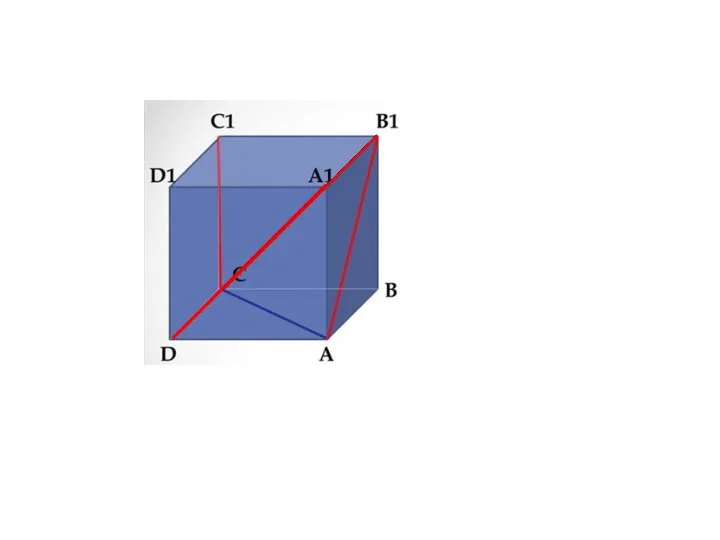
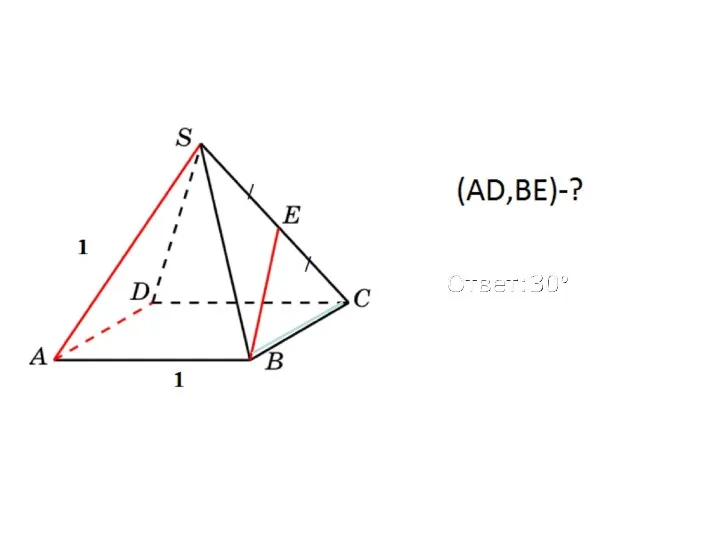
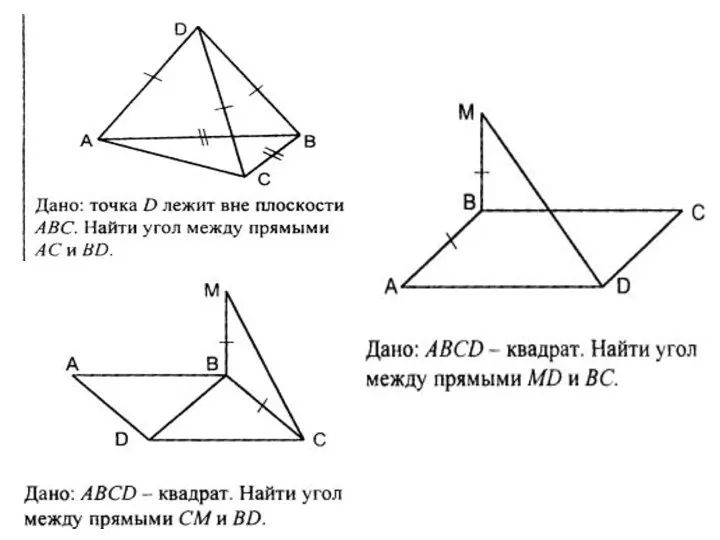
- 62. Угол между прямыми в пространстве Определение. Углом между двумя прямыми в пространстве называется наименьший из углов,
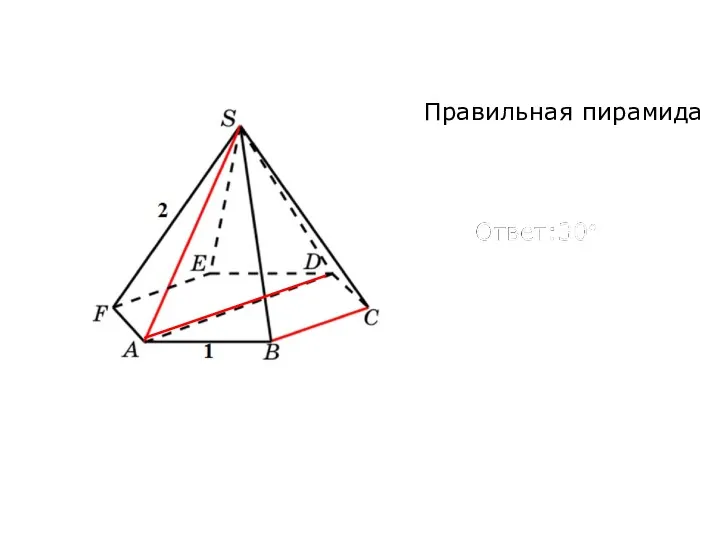
- 67. Правильная пирамида
- 68. Правильная пирамида
- 70. 1 – задание В кубе ABCDA1B1C1D1 найдите угол между прямыми: а) AB и BB1 b) BD
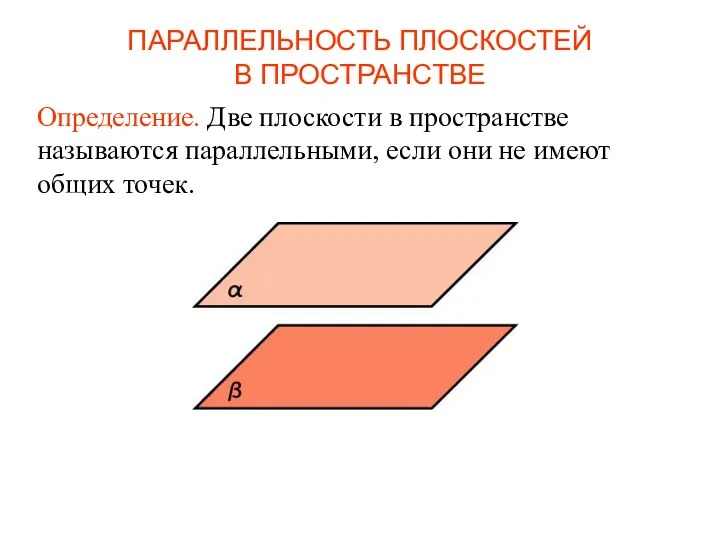
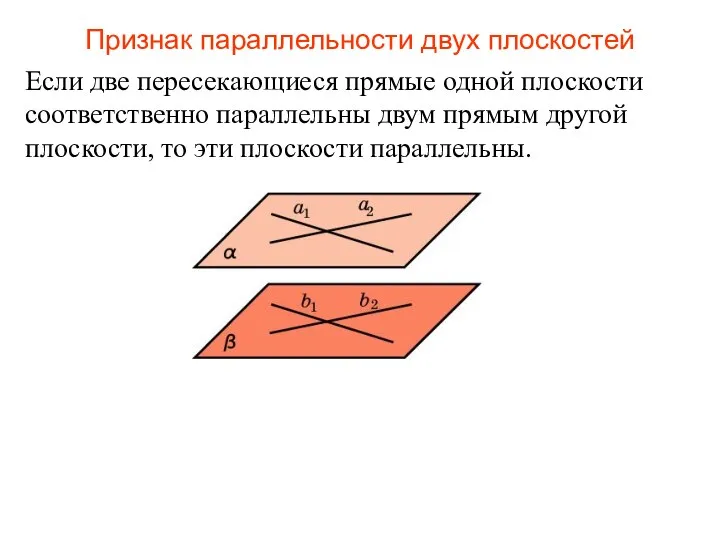
- 71. Определение. Две плоскости в пространстве называются параллельными, если они не имеют общих точек. ПАРАЛЛЕЛЬНОСТЬ ПЛОСКОСТЕЙ В
- 72. Если две пересекающиеся прямые одной плоскости соответственно параллельны двум прямым другой плоскости, то эти плоскости параллельны.
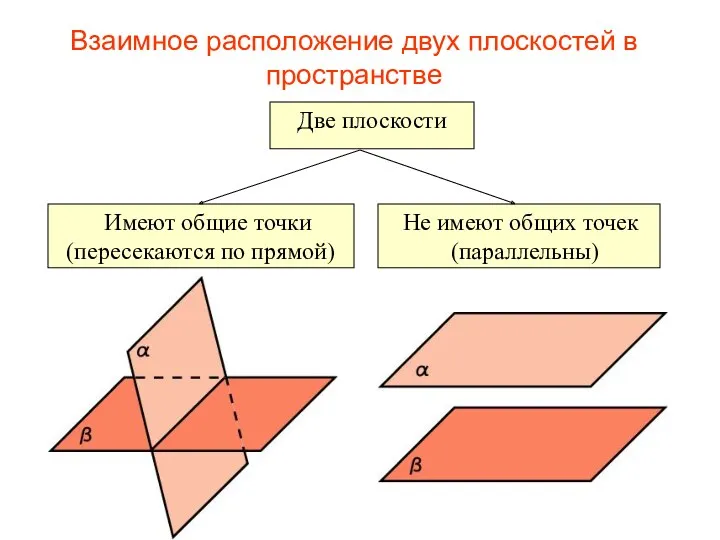
- 73. Взаимное расположение двух плоскостей в пространстве
- 74. Ответ: Нет. Верно ли утверждение: "Если прямая, лежащая в одной плоскости, параллельна прямой, лежащей в другой
- 75. Упражнение 2 Верно ли, что две плоскости, перпендикулярные третьей, параллельны? Ответ: Нет.
- 76. Ответ: Нет. Верно ли утверждение: "Если две прямые, лежащие в одной плоскости, параллельны двум прямым, лежащим
- 77. Упражнение 4 Сколько плоскостей, перпендикулярных данной плоскости, можно провести через данную прямую? Ответ: Бесконечно много, если
- 78. Ответ: Да. Могут ли быть параллельными две плоскости, проходящие через непараллельные прямые? Упражнение 5
- 79. Упражнение 6 Плоскость α перпендикулярна плоскости β. Будет ли всякая прямая плоскости α перпендикулярна плоскости β?
- 80. Ответ: Да. Могут ли пересекаться плоскости, параллельные одной и той же прямой? Упражнение 7
- 81. Упражнение 8 Плоскость и прямая параллельны. Верно ли утверждение о том, что плоскость, перпендикулярная данной плоскости,
- 82. Ответ: Нет. Через каждую из двух параллельных прямых проведена плоскость. Можно ли утверждать, что эти плоскости
- 83. Упражнение 10 Плоскость и прямая параллельны. Будет ли верно утверждение о том, что плоскость, перпендикулярная прямой,
- 84. ДВУГРАННЫЙ УГОЛ
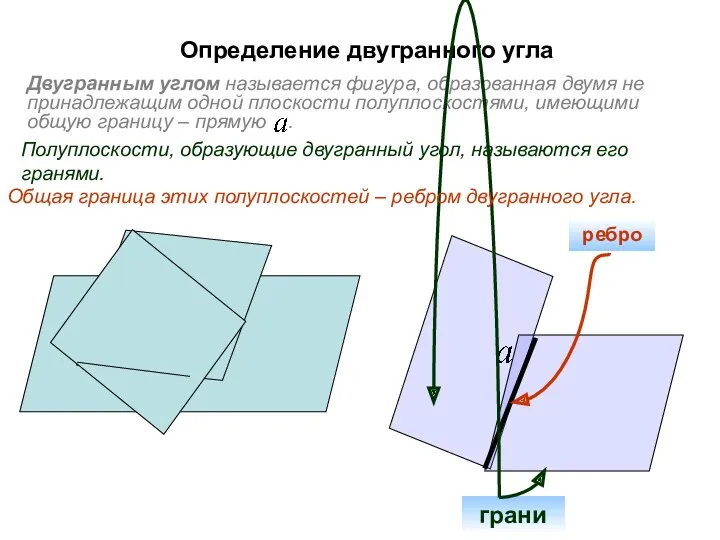
- 85. Определение двугранного угла Двугранным углом называется фигура, образованная двумя не принадлежащим одной плоскости полуплоскостями, имеющими общую
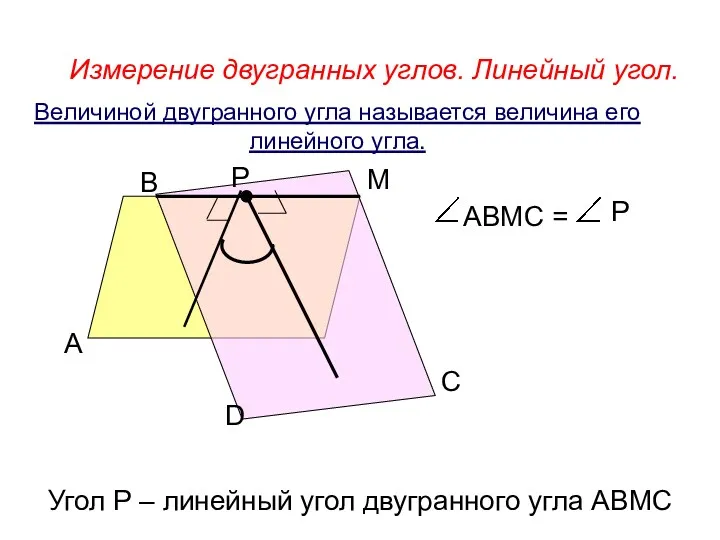
- 86. Измерение двугранных углов. Линейный угол. А В М D Р С АВМС = Р Угол Р
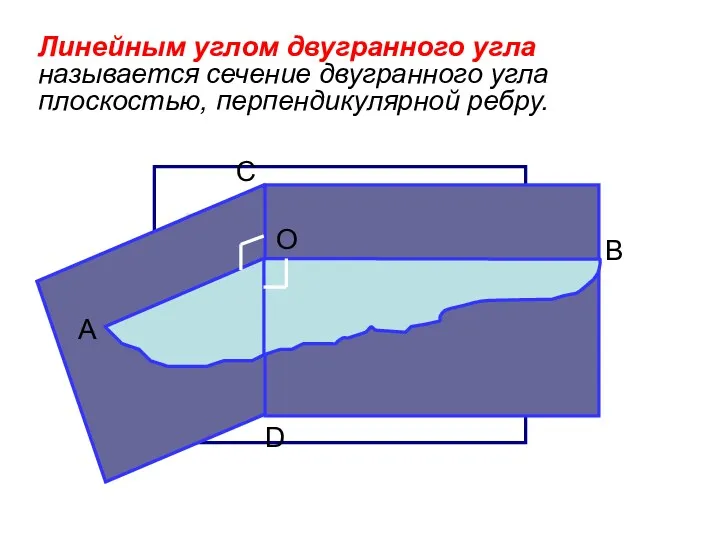
- 87. Линейным углом двугранного угла называется сечение двугранного угла плоскостью, перпендикулярной ребру.
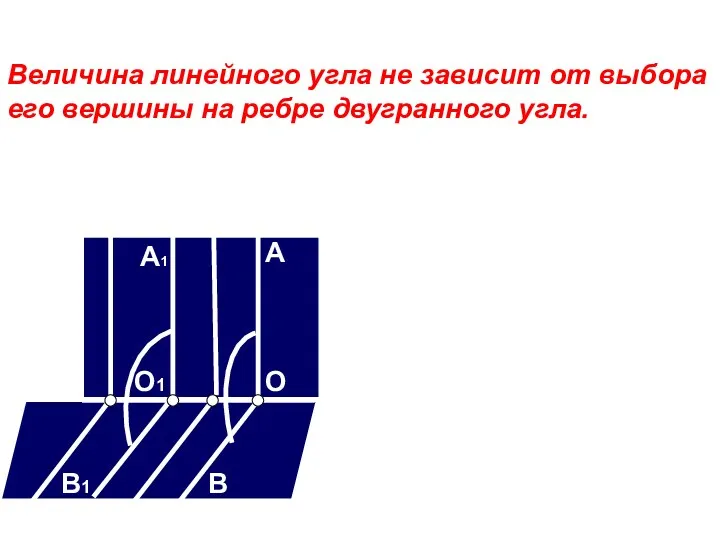
- 88. Величина линейного угла не зависит от выбора его вершины на ребре двугранного угла. A B O
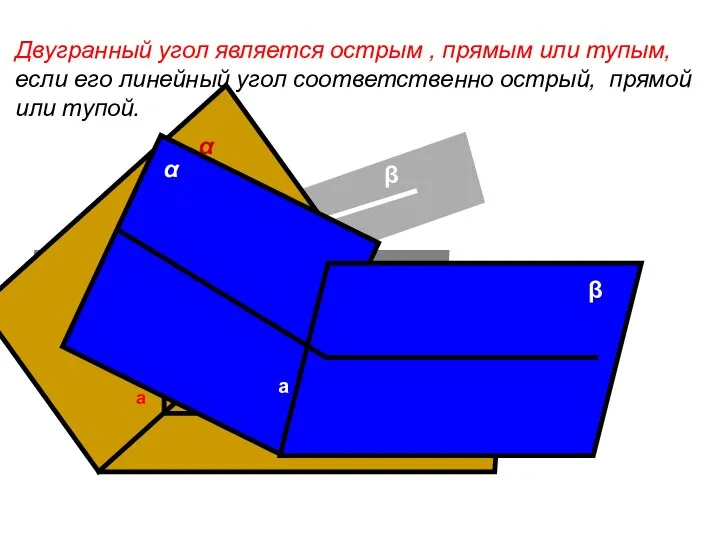
- 89. Двугранный угол является острым , прямым или тупым, если его линейный угол соответственно острый, прямой или
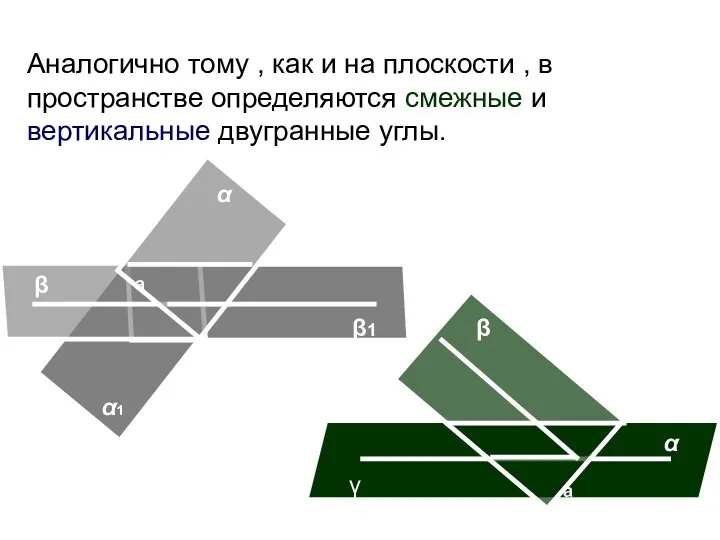
- 90. Аналогично тому , как и на плоскости , в пространстве определяются смежные и вертикальные двугранные углы.
- 91. Углом между двумя пересекающимися плоскостями называется наименьший из двугранных углов, образованных при их пересечении. Угол между
- 92. Работа в парах Уровень А. В кубе ABCDA1B1C1D1 найдите углы между плоскостями ABC1 и ABC. Уровень
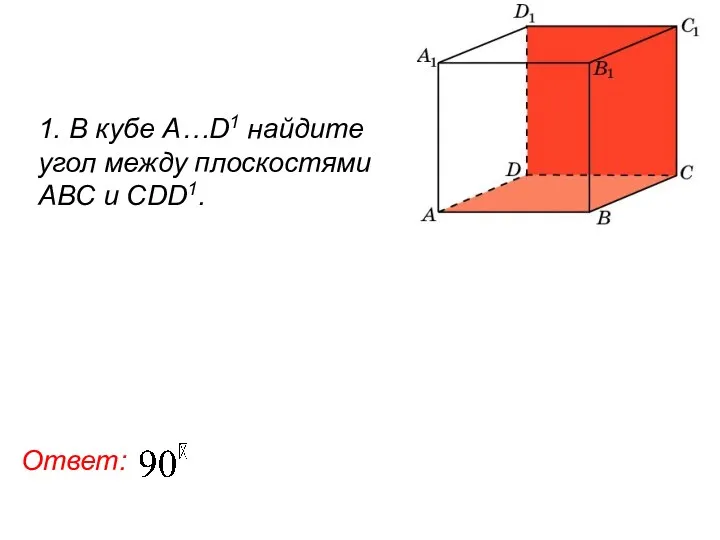
- 94. 1. В кубе A…D1 найдите угол между плоскостями ABC и CDD1. Ответ:
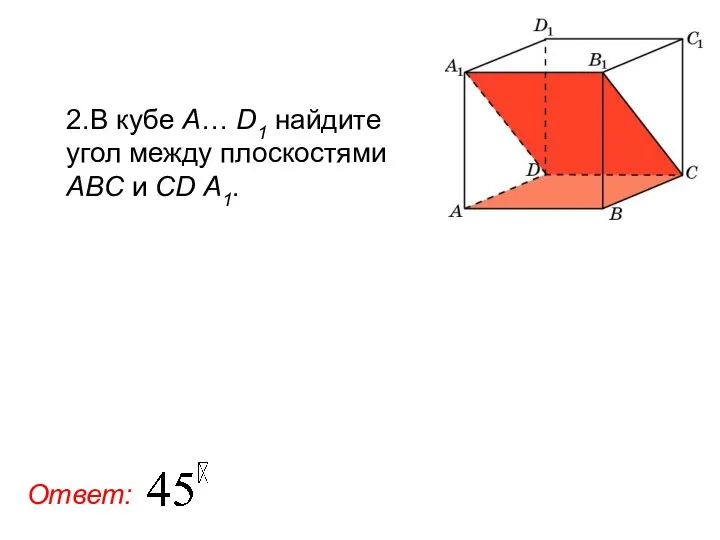
- 95. 2.В кубе A… D1 найдите угол между плоскостями ABC и CD А1. Ответ:
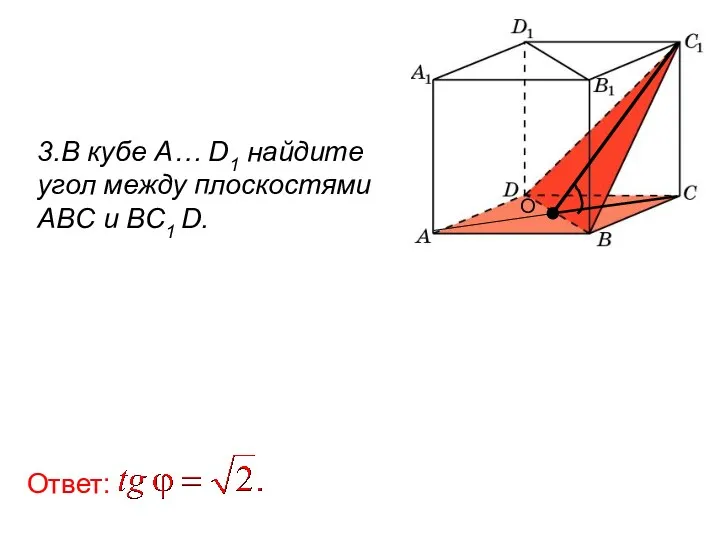
- 96. 3.В кубе A… D1 найдите угол между плоскостями ABC и BC1 D. Ответ: О
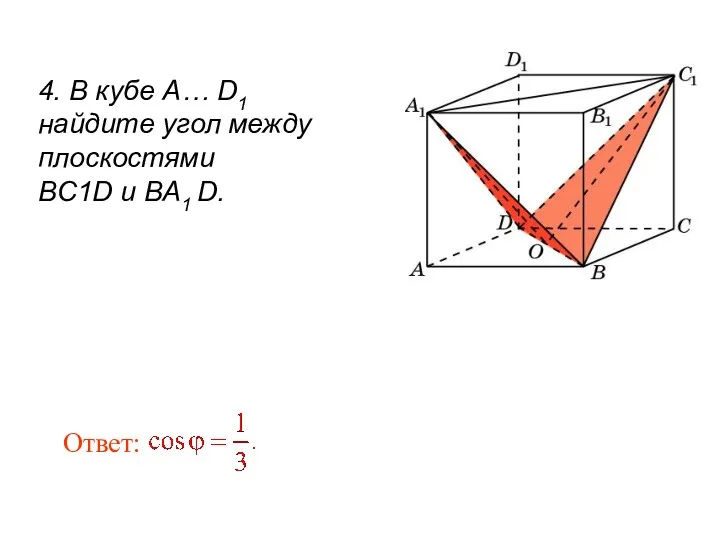
- 97. Ответ: 4. В кубе A… D1 найдите угол между плоскостями BC1D и BA1 D.
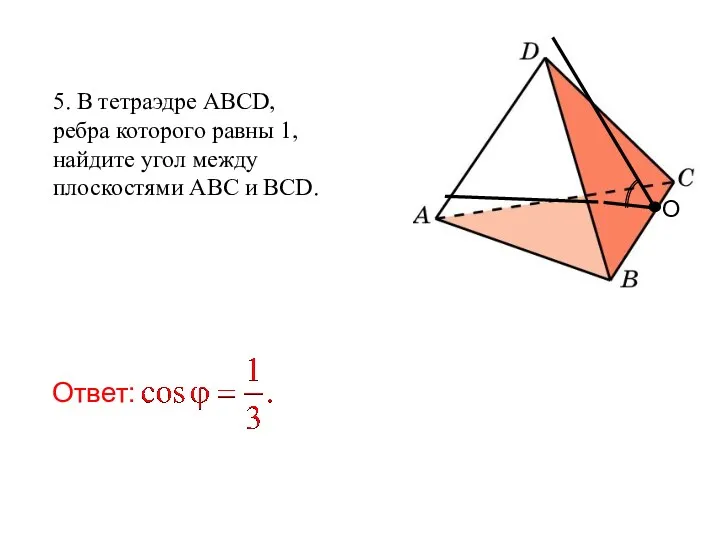
- 98. 5. В тетраэдре ABCD, ребра которого равны 1, найдите угол между плоскостями ABC и BCD. О
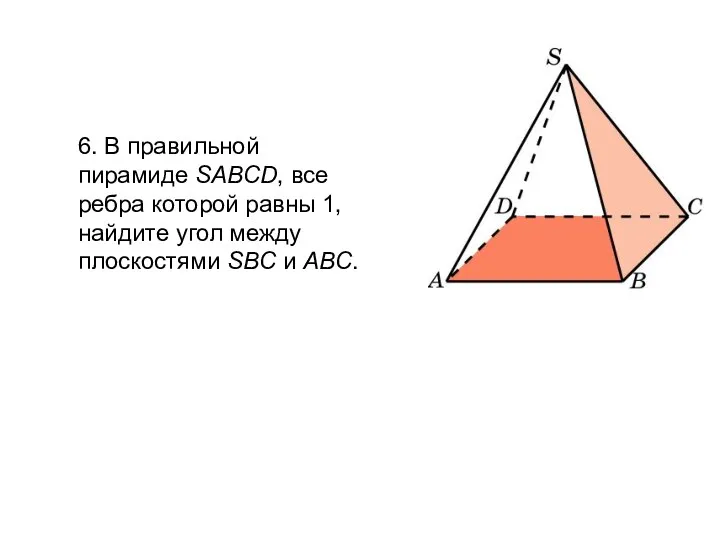
- 99. 6. В правильной пирамиде SABCD, все ребра которой равны 1, найдите угол между плоскостями SBC и
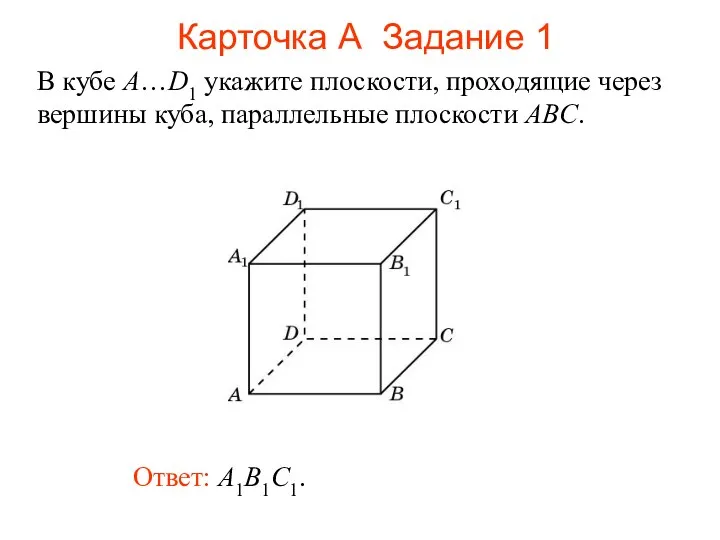
- 100. Ответ: A1B1C1. В кубе A…D1 укажите плоскости, проходящие через вершины куба, параллельные плоскости ABC. Карточка А
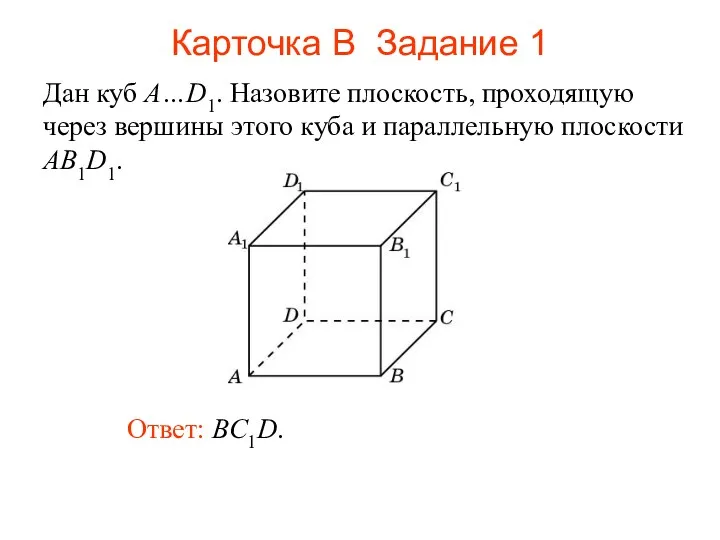
- 101. Ответ: BC1D. Дан куб A…D1. Назовите плоскость, проходящую через вершины этого куба и параллельную плоскости AB1D1.
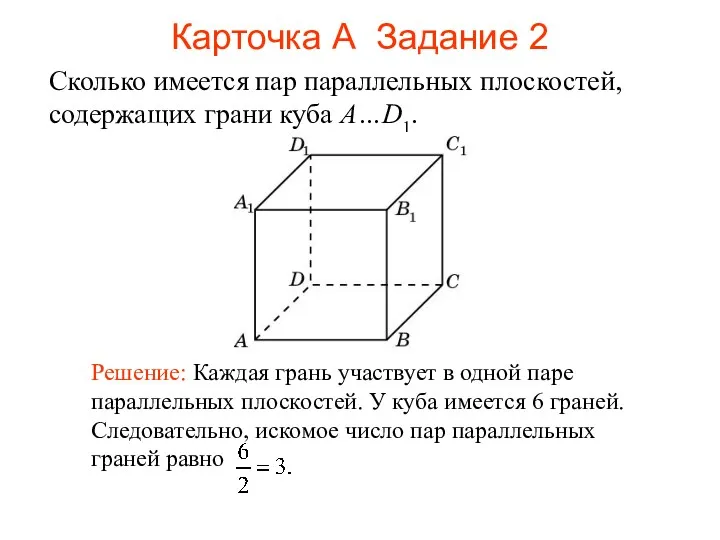
- 102. Сколько имеется пар параллельных плоскостей, содержащих грани куба A…D1. Карточка А Задание 2
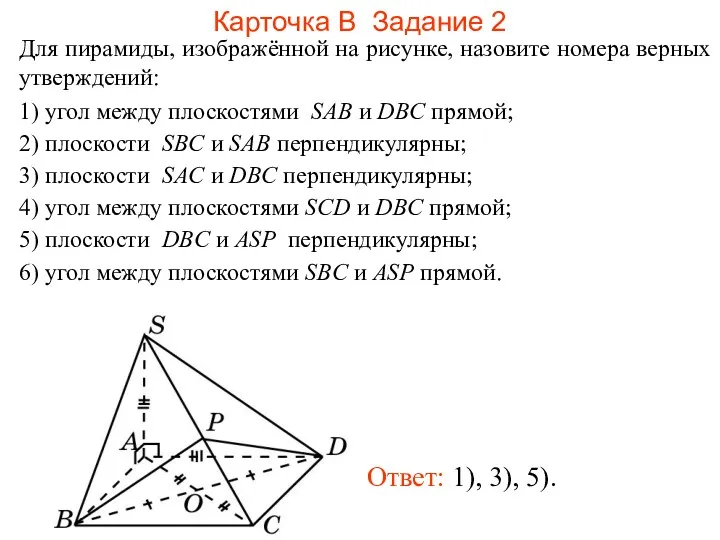
- 103. Карточка В Задание 2 Для пирамиды, изображённой на рисунке, назовите номера верных утверждений: 1) угол между
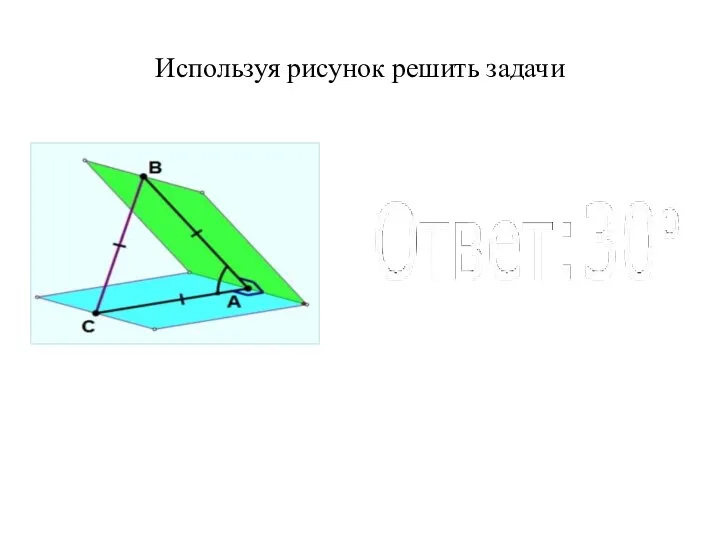
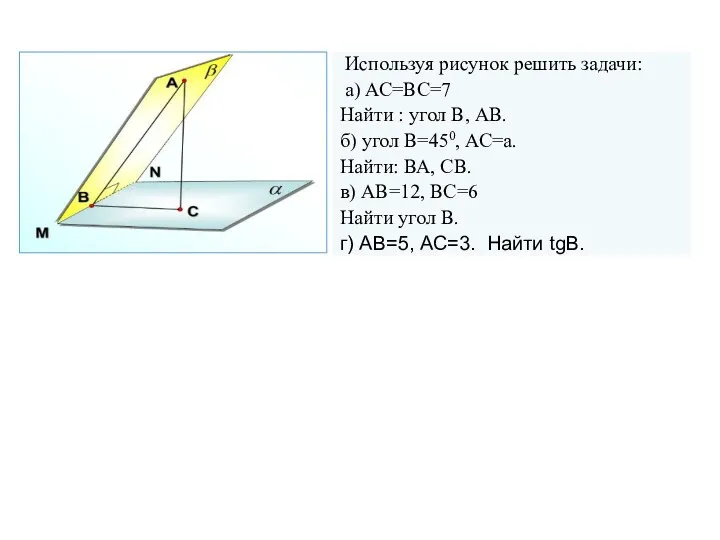
- 104. Используя рисунок решить задачи
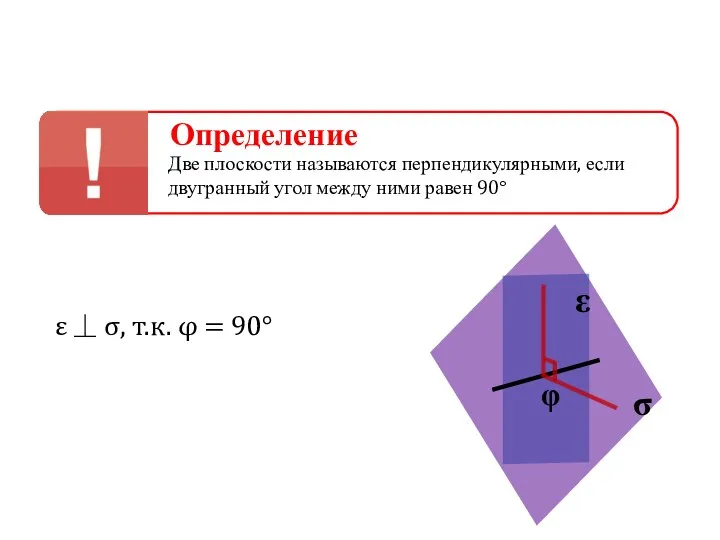
- 106. ε ⏊ σ, т.к. φ = 90° Определение Две плоскости называются перпендикулярными, если двугранный угол между
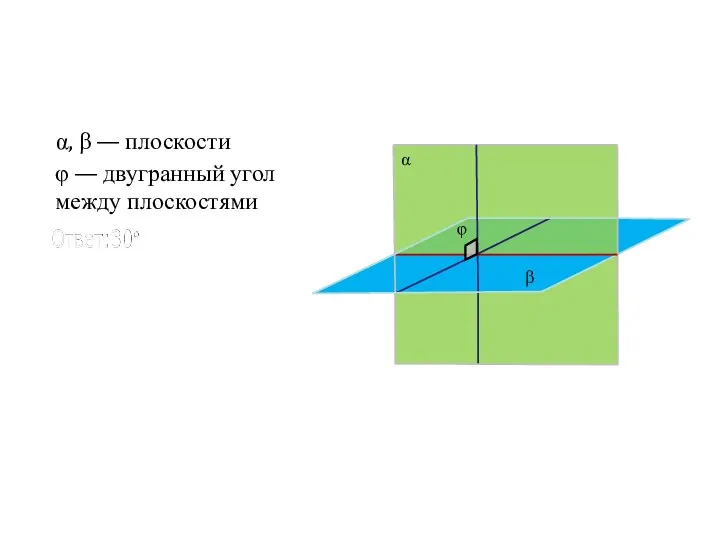
- 107. α, β — плоскости φ — двугранный угол между плоскостями α β φ
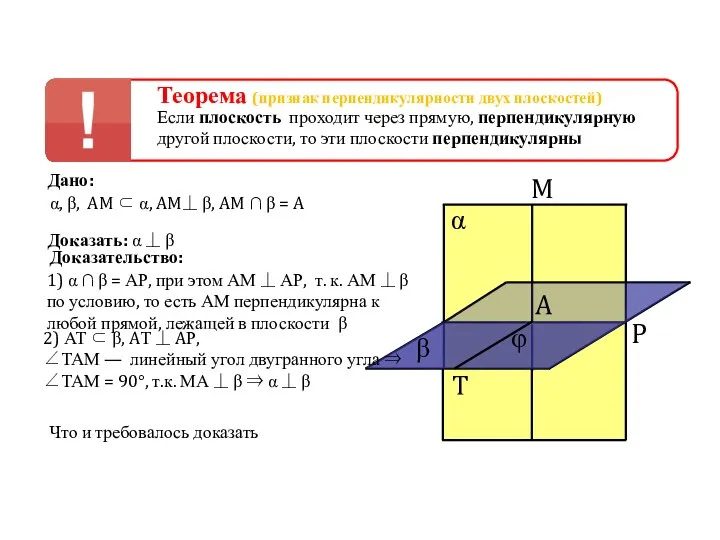
- 108. Теорема (признак перпендикулярности двух плоскостей) Если плоскость проходит через прямую, перпендикулярную другой плоскости, то эти плоскости
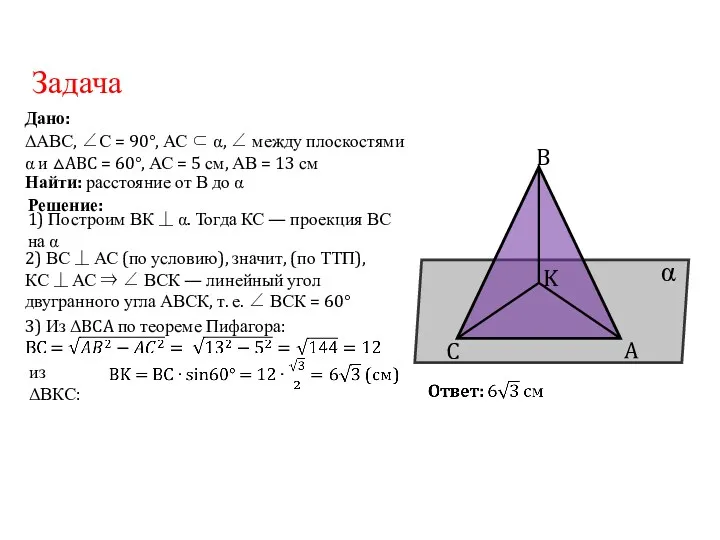
- 109. Дано: ΔАВС, ∠С = 90°, АС ⊂ α, ∠ между плоскостями α и △ABC = 60°,
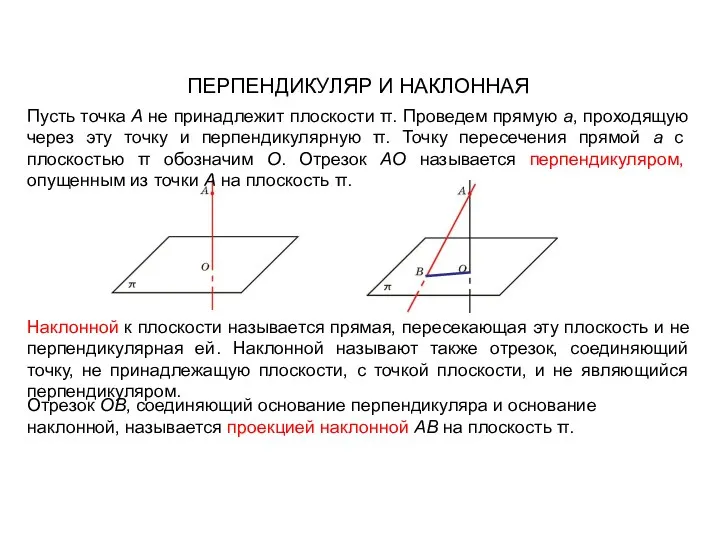
- 110. ПЕРПЕНДИКУЛЯР И НАКЛОННАЯ Пусть точка A не принадлежит плоскости π. Проведем прямую a, проходящую через эту
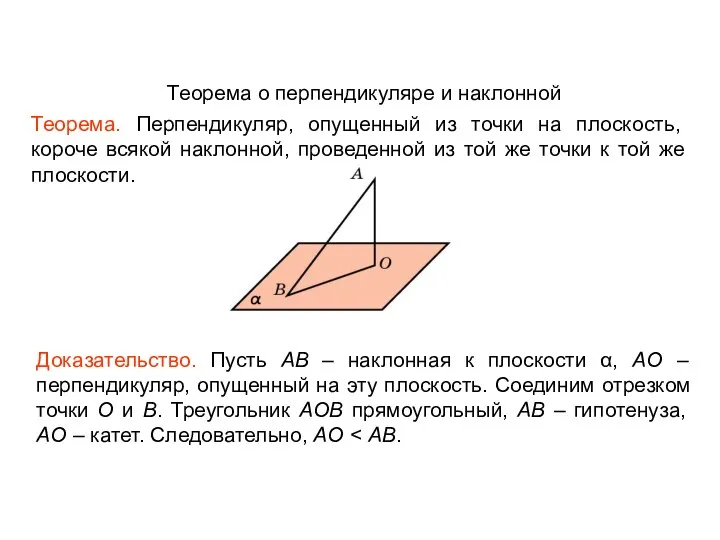
- 111. Теорема о перпендикуляре и наклонной Теорема. Перпендикуляр, опущенный из точки на плоскость, короче всякой наклонной, проведенной
- 113. Скачать презентацию































 Теория принятия решений. Статистические игры
Теория принятия решений. Статистические игры Подготовка к ЕГЭ. Площади фигур
Подготовка к ЕГЭ. Площади фигур Формула Бернулли
Формула Бернулли Прямоугольник
Прямоугольник Треугольник
Треугольник Сущность и содержание метрологии. (Лекция 1)
Сущность и содержание метрологии. (Лекция 1) Вивчаємо арифметичні дії множення і ділення
Вивчаємо арифметичні дії множення і ділення Царстве математики. 6 класс
Царстве математики. 6 класс Плоскость. Прямая. Луч. Демонстрационный материал
Плоскость. Прямая. Луч. Демонстрационный материал Угол между векторами. Скалярное произведение векторов. 11 класс
Угол между векторами. Скалярное произведение векторов. 11 класс Приемы устного быстрого счета. Гениальность или метод
Приемы устного быстрого счета. Гениальность или метод Нахождение числа по его дроби
Нахождение числа по его дроби Презентация Технология уровневой дифференциации.
Презентация Технология уровневой дифференциации. Подготовка к ЕГЭ В-13. Задачи
Подготовка к ЕГЭ В-13. Задачи презентация к уроку математики 4 класс по теме Деление на двузначное число
презентация к уроку математики 4 класс по теме Деление на двузначное число Прямая и обратная теоремы в свойствах и признаках параллелограмма
Прямая и обратная теоремы в свойствах и признаках параллелограмма Параллель және ортогональ проекциялау. Ортогональ проекцияның ауданы
Параллель және ортогональ проекциялау. Ортогональ проекцияның ауданы Презентация к уроку по математике (2 класс) по теме Письменный прием сложения вида 45+23
Презентация к уроку по математике (2 класс) по теме Письменный прием сложения вида 45+23 Презентация по математике Сложение и вычитание числа 1 и 2
Презентация по математике Сложение и вычитание числа 1 и 2 Квадрат. Свойства квадрата. Периметр квадрата
Квадрат. Свойства квадрата. Периметр квадрата Математическая игра Смекай, отгадывай, считай
Математическая игра Смекай, отгадывай, считай Математическая статистика
Математическая статистика Взаємне розміщення площини і кулі у просторі
Взаємне розміщення площини і кулі у просторі Освоение величин в дошкольном возрасте как условие познания окружающего мира
Освоение величин в дошкольном возрасте как условие познания окружающего мира Задачи на разностное сравнение.1кл.по программе Школа России
Задачи на разностное сравнение.1кл.по программе Школа России Точечные и интервальные оценки неизвестных параметров распределения
Точечные и интервальные оценки неизвестных параметров распределения МАТЕМАТИКАВОКРУГ НАС
МАТЕМАТИКАВОКРУГ НАС Представление статистических данных: таблицы и графики. Тема 4
Представление статистических данных: таблицы и графики. Тема 4