Содержание
- 2. СТАТИСТИЧЕСКИЕ ИГРЫ Игра с природой (статистическая игра) – это парная матричная игра, в которой сознательный игрок
- 3. РЕШЕНИЕ СТАТИСТИЧЕСКОЙ ИГРЫ 1. Следует исключить «заведомо невыгодные» стратегии игрока A из платежной матрицы. 2. Если
- 4. ПРИМЕР 1. НАЙТИ МАТРИЦУ РИСКОВ (А - МАТРИЦА ВЫИГРЫША). а21 = а24 = 3, однако они
- 5. В статистических играх существует две постановки задачи определения оптимальной стратегии: при одной желательно получить max выигрыш
- 6. 1. КРИТЕРИЙ БАЙЕСА Игроку A(статистику) должны быть известны вероятности, с которыми система (окружающая среда) находится в
- 7. средний выигрыш в этом случае при выборе стратегии Аi равен Если А - матрица выигрышей Если
- 8. 2. КРИТЕРИЙ НЕДОСТАТОЧНОГО ОСНОВАНИЯ ЛАПЛАСА Если есть основания считать состояния природы равновероятными то можно пользоваться критерием
- 9. ПРИМЕР 2. Крупный ресторан определяет уровень предложения услуг, чтобы удовлетворить потребности клиентов в предстоящие праздники. Точное
- 10. Пользуясь критерием Лапласа и полагая Р(Пi) = 0,25, находим среднее значение затрат По критерию Лапласа наилучший
- 11. 3. МАКСИМИННЫЙ (МИНИМАКСНЫЙ) КРИТЕРИЙ ВАЛЬДА Игра с природой ведется как игра с разумным, причем агрессивным противником
- 12. 4. КРИТЕРИЙ МИНИМАКСНОГО РИСКА СЭВИДЖА Критерий крайнего пессимизма, рекомендует выбирать стратегию, обеспечивающую в наихудших условиях минимальный
- 13. 5. КРИТЕРИЙ ПЕССИМИЗМА-ОПТИМИЗМА ГУРВИЦА Крайнему пессимизму можно противопоставить крайний оптимизм (критерий азартного игрока), когда ставка делается
- 14. - критерий Гурвица превращается в критерий Вальда (крайний пессимизм) – критерий крайнего оптимизма (максимальный выигрыш в
- 15. ПРИМЕР 2 (ПРОДОЛЖЕНИЕ) Выберем λ = 1/2. 25 ⋅ 0,5 + 5 ⋅ 0,5 = 15
- 16. ЗАКЛЮЧЕНИЕ. В рассматриваемом примере получили: - по критерию Лапласа – А2, потери 11,5 - по критерию
- 17. ПРИМЕР 3. Швейная фабрика должна израсходовать в апреле 3 500 000 руб. на пошив мужских брюк
- 18. Построим матрицу выигрышей а11 = 500 ⋅ 2000 + 1200 ⋅ 4500 – 3 500 000
- 19. РЕШЕНИЕ Критерии Лапласа – А2 Критерий Вальда – А1 и А2 равнооптимальны Критерий Сэвиджа – А2.
- 20. ПРИМЕР 4 Ежедневный спрос на булочки в продовольственном магазине может принимать следующее значение: 100, 150, 200,
- 21. РЕШЕНИЕ Критерии Лапласа – 250 булочек Критерий Вальда – 100 булочек Критерий Сэвиджа – 250 булочек
- 22. ПРИМЕР 5 Вокзал определяет количество транспортных средств для удовлетворения потребностей пассажиров в праздничные дни. Точное число
- 23. РЕШЕНИЕ Критерии Лапласа – А2 Критерий Вальда – А3 Критерий Сэвиджа – А2. Критерий Гурвица (λ
- 25. Скачать презентацию






















 Формулы сокращённого умножения. 7 класс (учебник Алгебра-7, Макарычев Ю.Н., 2008г.)
Формулы сокращённого умножения. 7 класс (учебник Алгебра-7, Макарычев Ю.Н., 2008г.) Модели рационального спектра. Тема 3
Модели рационального спектра. Тема 3 Тригонометрия. Таблица значений тригонометрических функций
Тригонометрия. Таблица значений тригонометрических функций Я выбираю здоровый образ жизни! О вреде курения языком математики
Я выбираю здоровый образ жизни! О вреде курения языком математики Подготовка к контр работе. Решение задач по теме: площади. Теорема Пифагора.(первый урок)
Подготовка к контр работе. Решение задач по теме: площади. Теорема Пифагора.(первый урок) Круги Эйлера. Решение задач
Круги Эйлера. Решение задач Множества. Операции над множествами
Множества. Операции над множествами Действия со степенью
Действия со степенью Математика вокруг нас. Орнаменты и узоры на посуде
Математика вокруг нас. Орнаменты и узоры на посуде Считаем до 10. Тренажёр 1 класс
Считаем до 10. Тренажёр 1 класс Презентация к уроку Уравнение. Проверка решения уравнения
Презентация к уроку Уравнение. Проверка решения уравнения Основы образования чертежа. Проецирование плоскости. Метрические задачи. (Лекция 2)
Основы образования чертежа. Проецирование плоскости. Метрические задачи. (Лекция 2) Многогранники. Призма
Многогранники. Призма Презентация Система заданий по формированию регулятивных УУД на уроках математики в 1 классе, комментарий к слайдам
Презентация Система заданий по формированию регулятивных УУД на уроках математики в 1 классе, комментарий к слайдам Векторная алгебра. Линейные операции над векторами
Векторная алгебра. Линейные операции над векторами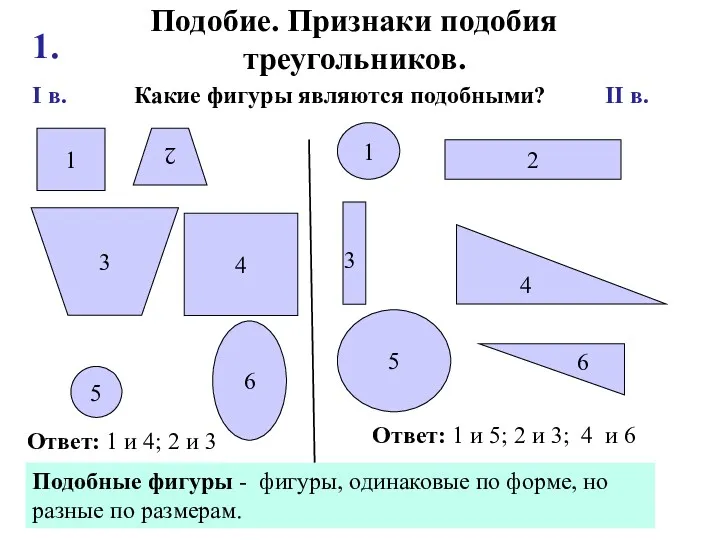 Подобие. Признаки подобия треугольников
Подобие. Признаки подобия треугольников Центральные и вписанные углы
Центральные и вписанные углы Проценты
Проценты Пример решения транспортной задачи (открытая модель)
Пример решения транспортной задачи (открытая модель) Умножение и деление круглых чисел. Урок по математике в 3 классе
Умножение и деление круглых чисел. Урок по математике в 3 классе Презентация Ох, уж эта математика
Презентация Ох, уж эта математика Задачи с величинами: цена, количество, стоимость
Задачи с величинами: цена, количество, стоимость Элементы комбинаторики. Способы решения комбинаторных задач
Элементы комбинаторики. Способы решения комбинаторных задач Задачи на смекалку
Задачи на смекалку Комплексные числа
Комплексные числа Физико-математическое лото. 8 класс
Физико-математическое лото. 8 класс Интерактивное занятие для дошкольников. Дистанционное обучение.
Интерактивное занятие для дошкольников. Дистанционное обучение. Метр — одиниця довжини
Метр — одиниця довжини