Содержание
- 2. Аксиоматика Колмогорова Пусть Ω — пространство элементарных исходов некоторого случайного эксперимента. Набор подмножеств Ω будет называться
- 3. σ - алгебра событий Множество Ψ, состоящее из подмножеств множества Ω, называется σ - алгеброй событий,
- 4. Первая группа аксиом Колмогорова Этого набора аксиом достаточно для замкнутости множества Ψ относительно других операций над
- 5. Пример @ Пусть Ω = {1, 2, 3, 4, 5, 6} - пространство элементарных исходов (например,
- 6. Вторая группа аксиом Колмогорова Для любого события А ∈ Ψ его вероятностная мера неотрицательна: P(А) ≥
- 7. Основные формулы теории вероятностей Тройка (Ω, Ψ,Р) , в которой Ω - пространство элементарных исходов, Ψ
- 8. Основные формулы теории вероятностей Доказательство по аксиомам 2,3 второй группы c Доказательство По аксиоме 1 второй
- 9. Основные формулы теории вероятностей Доказательство так как c А ⊆ В - на языке теории множеств
- 10. Основные формулы теории вероятностей Доказательство c
- 11. Пример @ Из колоды (52 карты) вынули 10 карт. Найти вероятность того, что выбран хотя бы
- 12. Теорема сложения вероятностей Доказательство c Вероятность суммы событий A и B , находится по формуле: A
- 13. Теорема сложения вероятностей Вероятность суммы событий A1 , A2 , …., An , находится по формуле:
- 14. Условная вероятность и теорема умножения Условной вероятностью события А, при условии, что произошло событие В ,
- 15. Пример @ Кубик подбрасывается один раз. Известно, что выпало более трех очков. Какова при этом вероятность
- 16. Независимые события и теорема умножения События A и B называются независимыми, если P (A ∩ B)
- 17. Формула полной вероятности События Н1, Н2 …, образующие полную группу событий, часто называют гипотезами. При подходящем
- 18. Формула полной вероятности Пусть Н1, Н2 , … - полная группа событий. Тогда вероятность любого события
- 19. Пример @ Имеется три партии деталей. Процент годных составляет соответственно 89 %, 92% и 97% .
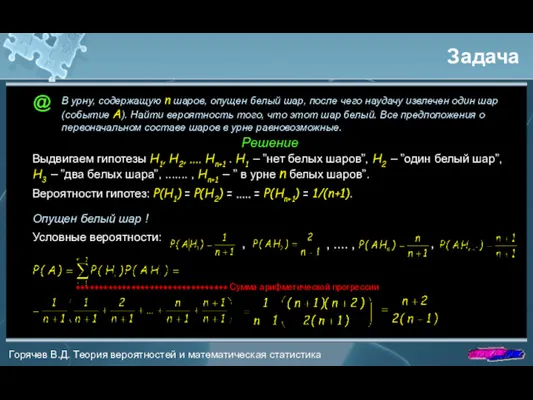
- 20. Задача @ В урну, содержащую n шаров, опущен белый шар, после чего наудачу извлечен один шар
- 21. Апостериорная вероятность. Формула Байеса. Важное значение в теории вероятностей имеет формула Байеса. Это соотношение справедливо, если
- 23. Скачать презентацию



















 Умножение и деление. Задачи
Умножение и деление. Задачи Узоры и орнаменты на посуде. Проект по математике
Узоры и орнаменты на посуде. Проект по математике Подготовка к ГИА по математике. Задания 9
Подготовка к ГИА по математике. Задания 9 Математические отношения
Математические отношения Задача по финансовой математике
Задача по финансовой математике Занимательный материал №3
Занимательный материал №3 Симметрия. Симметричные фигуры
Симметрия. Симметричные фигуры Предел числовой последовательности
Предел числовой последовательности ГИА - 2012. Открытый банк заданий по математике. (Задача 8)
ГИА - 2012. Открытый банк заданий по математике. (Задача 8) Учусь считать
Учусь считать Векторная алгебра. Вектор - направленный отрезок
Векторная алгебра. Вектор - направленный отрезок Правильні многокутники. (9 клас)
Правильні многокутники. (9 клас) Геометрические фигуры
Геометрические фигуры Логарифмические уравнения
Логарифмические уравнения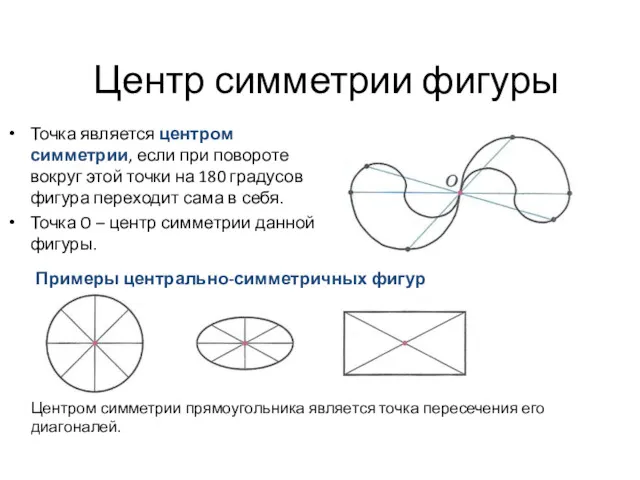 Центр симметрии фигуры
Центр симметрии фигуры Линейная и квадратичная функции и их графики
Линейная и квадратичная функции и их графики Формулы сокращенного умножения
Формулы сокращенного умножения Интерактивное пособие для подготовки к ОГЭ. Окружность
Интерактивное пособие для подготовки к ОГЭ. Окружность Ознакомление с задачей в 2 действия
Ознакомление с задачей в 2 действия Урок математики во 2 классе
Урок математики во 2 классе Приемы быстрого счета
Приемы быстрого счета Путешествие в страну натуральных чисел. Урок-игра. 5 класс
Путешествие в страну натуральных чисел. Урок-игра. 5 класс Дифференциальное исчисление функций одной переменной
Дифференциальное исчисление функций одной переменной Математика. Место и содержание курса
Математика. Место и содержание курса Нелинейные модели регрессии. (Лекция 7)
Нелинейные модели регрессии. (Лекция 7) Сравнение дробей 4 класс.
Сравнение дробей 4 класс. Применение распределительного свойства умножения
Применение распределительного свойства умножения Прямоугольный параллелепипед
Прямоугольный параллелепипед