Содержание
- 2. Литература к курсу Аляев Ю.А., Тюрин С.Ф. Дискретная математика и математическая логика – М.: Финансы и
- 3. Темы лекции 1. Высказывания и операции над ними Формулы алгебры высказываний Тавтологии алгебры высказываний Логическая равносильность
- 4. Понятие высказывания Опр. Высказывание – предложение, о котором можно судить истинно оно или ложно. Высказывание не
- 5. Примеры высказываний A1: Слоны умеют летать A2: Воздух – это смесь газов A3: 27>104 B1: Подосиновик
- 6. Функция истинности 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. λ– Функция истинности, Значение λ(P) –
- 7. Отрицание высказывания 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Отрицанием высказывания P называется новое
- 8. Конъюнкция двух высказываний 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Конъюнкцией двух высказываний P
- 9. Дизъюнкция двух высказываний 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Дизъюнкцией двух высказываний P
- 10. Импликация двух высказываний 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Импликация двух высказываний P
- 11. Эквивалентность двух высказываний 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Эквивалентностью двух высказываний P
- 12. Понятие формулы алгебры высказываний 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Пропозиционная переменная –
- 13. Примеры 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Формулы алгебры высказываний 1.(X ↔Y) 2.((X ⋀
- 14. Логическое значение составного высказывания 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Если в формулу алгебры
- 15. Составление таблиц истинности для формул 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Пример Составить таблицу
- 16. Классификация формул алгебры высказываний 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Формула алгебры высказываний
- 17. Основные тавтологии Ч.1 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. 1.Закон исключённого третьего: P ⋁
- 18. Основные тавтологии Ч.2 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. 10.Правило «modus ponens»: (P ⋀
- 19. Свойства конъюнкции и дизъюнкции 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Следующие формулы алгебры высказываний
- 20. Свойства импликации и эквивалентности Ч.1 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Следующие формулы алгебры
- 21. Свойства импликации и эквивалентности Ч.2 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Следующие формулы алгебры
- 22. Выражение одних логических операций через другие 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Следующие формулы
- 23. Основные правила получения тавтологий 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Т. (правило заключения) Если
- 24. Понятие равносильности формул 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Формулы F(X1, X2, …,
- 25. Признак равносильности формул 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Т. (признак равносильности формул) Две
- 26. Равносильные преобразования формул 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Лемма (о замене) Если G(Y1,
- 27. Примеры равносильного преобразования 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Задача Упростить формулу ((P →
- 28. Понятие нормальных форм 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Конъюнктивным одночленом от переменных
- 29. Совершенные нормальные формы 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Одночлен (конъюнктивный или дизъюнктивный)
- 30. Представление формул алгебры высказываний СДНФ 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Т. (о представлении
- 31. Пример нахождения СДНФ 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Задача Для формулы (X ⋁
- 32. Пример нахождения СДНФ 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Задача Для формулы (X ⋁
- 33. Представление формул алгебры высказываний СКНФ 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Т. (о представлении
- 34. Пример нахождения СКНФ 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Задача Для формулы ((X ⋁
- 35. Пример нахождения СКНФ 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Задача Для формулы ((X ⋁
- 36. Понятие логического следствия 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Опр. Формула H(X1, X2, …,
- 37. Пример логического следствия 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Задача Определить справедливо ли следующее
- 38. Признаки и свойства логического следствия 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Т. (признак логического
- 39. Следование и равносильность формул 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. T. Две формулы алгебры
- 40. Правила логических умозаключений Ч.1 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Правило modus ponens Правило
- 41. Правила логических умозаключений Ч.2 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Правило цепного заключения Правило
- 42. Нахождение следствий из данных посылок 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Т. Формула H(X1,
- 43. Пример: Нахождение следствий из данных посылок 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Задача Найти
- 44. Нахождение посылок для данного следствия 1.Алгебра высказываний. Логика и теория алгоритмов, Аксёнов С.В. Т. Чтобы найти
- 46. Скачать презентацию
 Анализ одномерных распределений
Анализ одномерных распределений Сумма векторов. Задания для устного счета. Упражнение 14
Сумма векторов. Задания для устного счета. Упражнение 14 Третий признак равенства треугольников
Третий признак равенства треугольников Окружность и круг
Окружность и круг Последовательность Фибоначчи. Парадоксы с площадью
Последовательность Фибоначчи. Парадоксы с площадью Цилиндр. Сечение цилиндра плоскостями
Цилиндр. Сечение цилиндра плоскостями Основы алгебры логики
Основы алгебры логики Корень n-й степени
Корень n-й степени Решение задач с помощью уравнений
Решение задач с помощью уравнений График функции
График функции Как найти неизвестное вычитаемое
Как найти неизвестное вычитаемое Раскрытие скобок. Математика. 6 класс
Раскрытие скобок. Математика. 6 класс Приведенная система вычетов
Приведенная система вычетов Угол. Прямой угол
Угол. Прямой угол Распределение средств семейного бюджета
Распределение средств семейного бюджета Комплексные числа и действия над ними
Комплексные числа и действия над ними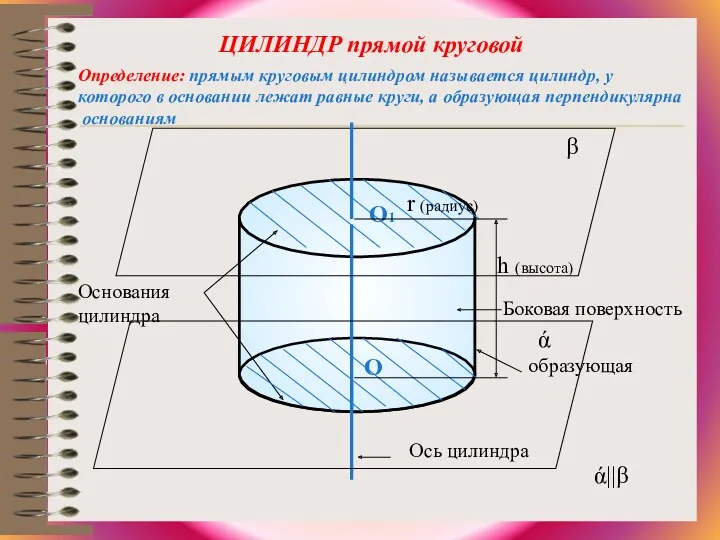 цилиндр
цилиндр Переместительный способ.
Переместительный способ. Засели домики (игра-тренажёр). 1 класс
Засели домики (игра-тренажёр). 1 класс Письменные приёмы сложения и вычитания многозначных чисел
Письменные приёмы сложения и вычитания многозначных чисел Двугранный угол
Двугранный угол Виды стохастических задач на уроках математики
Виды стохастических задач на уроках математики Целое и части
Целое и части Множественная регрессия в матричной форме
Множественная регрессия в матричной форме Математика Тема: Королевство математики
Математика Тема: Королевство математики Соотношение между сторонами и углами треугольника. Решение задач
Соотношение между сторонами и углами треугольника. Решение задач Математика. 5 класс. Найди правильный ответ:
Математика. 5 класс. Найди правильный ответ: Треугольники. Подготовка к ОГЭ. Задание 16
Треугольники. Подготовка к ОГЭ. Задание 16