Содержание
- 2. 5. Если R ≠ ∅, то переход к п. 2, иначе к п. 6; 1. В
- 3. 10. Составляется конъюнкция П’ = ∧ti. Раскрываются скобки. В полученной дизъюнкции на основе законов булевой алгебры
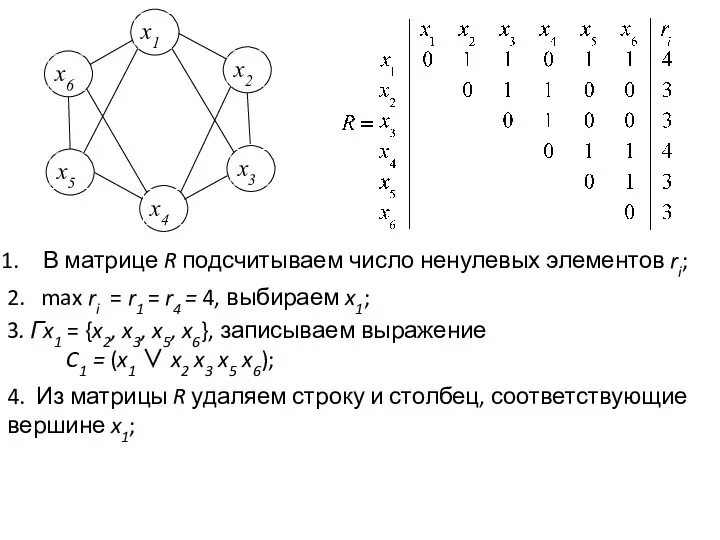
- 4. В матрице R подсчитываем число ненулевых элементов ri; 3. Гx1 = {x2, x3, x5, x6}, записываем
- 5. 5. R ≠ ∅, max ri = r4 = 4; Гx4 = {x2, x3, x5, x6},
- 6. 12. Составляем конъюнкцию Ci и выполняем минимизацию П = ∧Ci = C1 C2 C4 C5 =
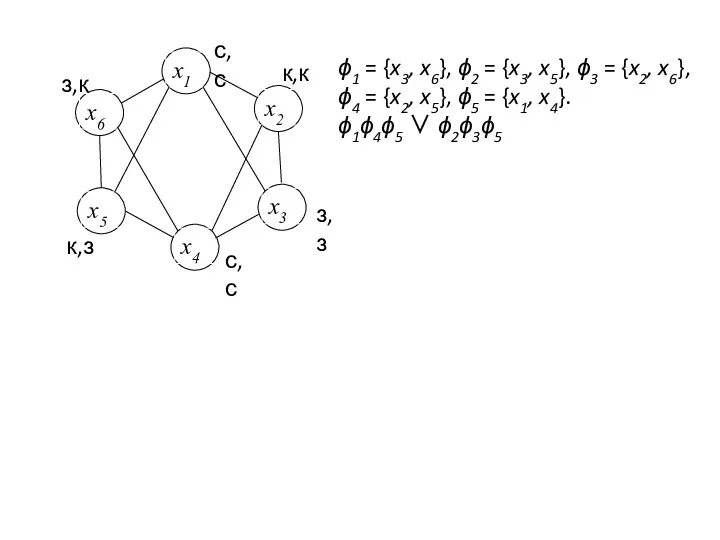
- 7. ϕ1 = {x3, x6}, ϕ2 = {x3, x5}, ϕ3 = {x2, x6}, ϕ4 = {x2, x5},
- 8. Недостатком точных алгоритмов является низкое быстродействие. Поэтому на практике используют приближенные алгоритмы, примером которых может служить
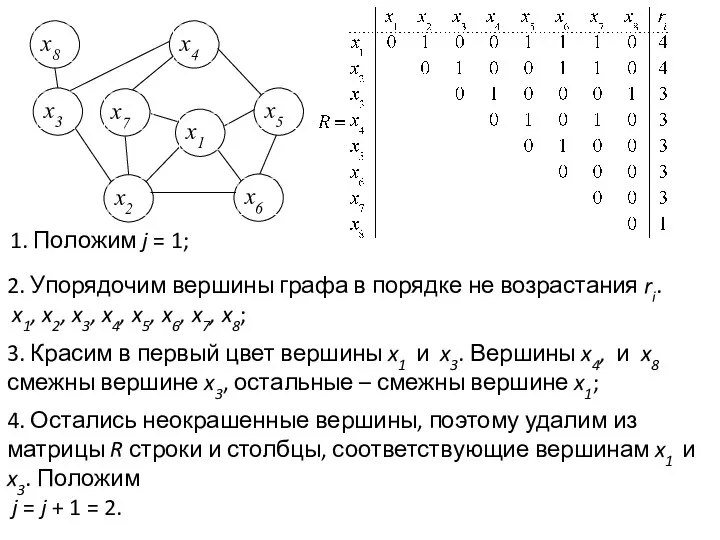
- 9. 1. Положим j = 1; 2. Упорядочим вершины графа в порядке не возрастания ri. x1, x2,
- 10. 5. Упорядочим вершины графа в порядке не возрастания ri: x2, x4, x5, x6, x7, x8; 6.
- 11. Достоинство алгоритма – быстродействие. Недостаток – не оптимальность. Для раскраски вершин графа приближенным алгоритмом потребовалось четыре
- 12. Кратчайшие пути Пусть дан граф G(X, Γ), ребрам которого приписаны веса, заданные матрицей C=||cij||m×m. Задача о
- 13. 1. Положить l(s)=0+ и считать эту пометку постоянной. Положить l(xi)=∞ для всех xi ≠ s и
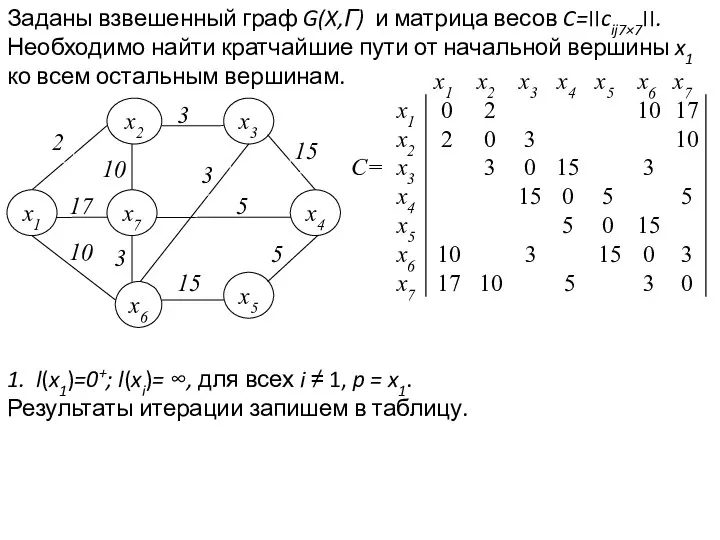
- 14. Заданы взвешенный граф G(X,Г) и матрица весов C=׀׀cij׀׀7×7. Необходимо найти кратчайшие пути от начальной вершины x1
- 15. 2. Гp ={x2, x6, x7} – все пометки временные, уточним их: l(x2)=min[∞ ,0++2]=2; l(x6)=min[∞, 0++10]=10; l(x7)=min[∞,
- 16. 6. l(xi*) = min[l(xi)] = l(x3) = 5. 7. l(x3) = 5+, p=x3. 8. Не все
- 17. 12. l(xi*) = min[l(xi)] = l(x7) = 11. 13. l(x7) = 11+, p=x7. 14. Не все
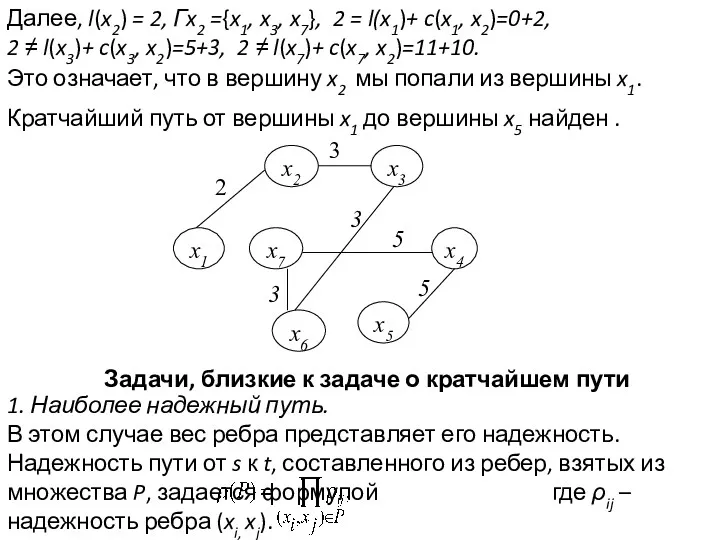
- 18. Кратчайшие расстояния от вершины x1 до всех вершин найдены. Как найти кратчайший путь до конкретной вершины,
- 19. Далее, l(x2) = 2, Гx2 ={x1, x3, x7}, 2 = l(x1)+ c(x1, x2)=0+2, 2 ≠ l(x3)+
- 20. 2. Самый длинный (критический) путь. Задача сетевого планирования, заключающаяся в нахождении самого длинного по временной протяженности
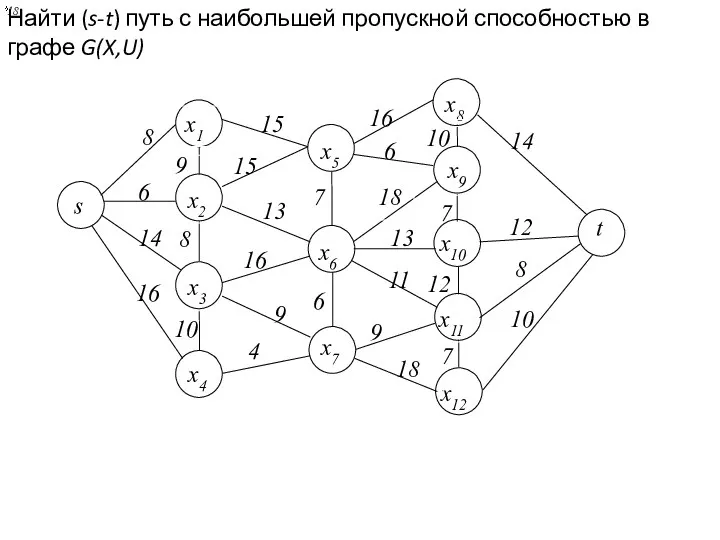
- 21. Теорема Форда – Фалкерсона. Пропускная способность пути с наибольшей пропускной способностью от s к t равна
- 22. Найти (s-t) путь с наибольшей пропускной способностью в графе G(X,U) 18 18
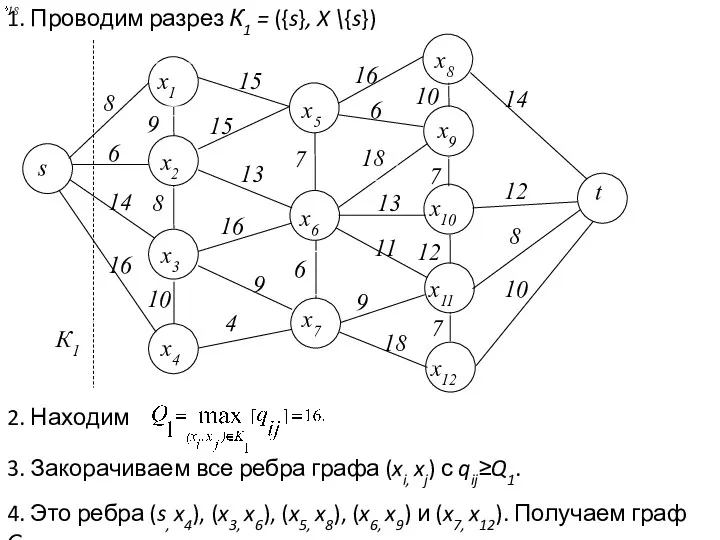
- 23. 1. Проводим разрез К1 = ({s}, X \{s}) 18 2. Находим 3. Закорачиваем все ребра графа
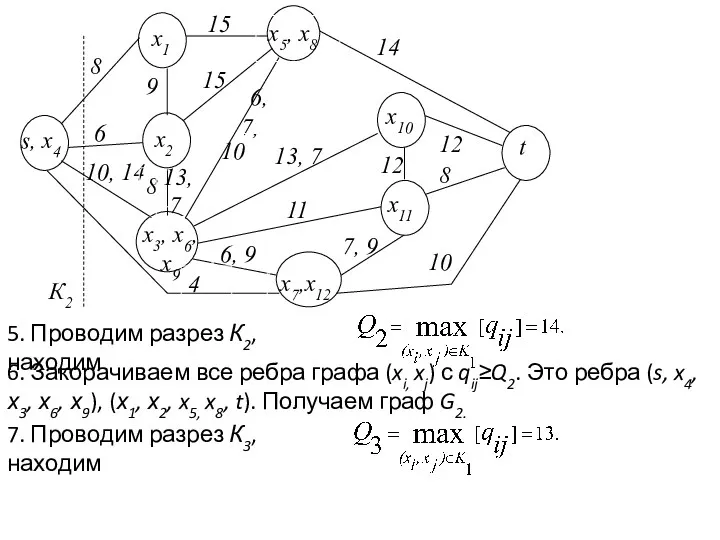
- 24. 5. Проводим разрез К2, находим 6. Закорачиваем все ребра графа (xi, xj) с qij≥Q2. Это ребра
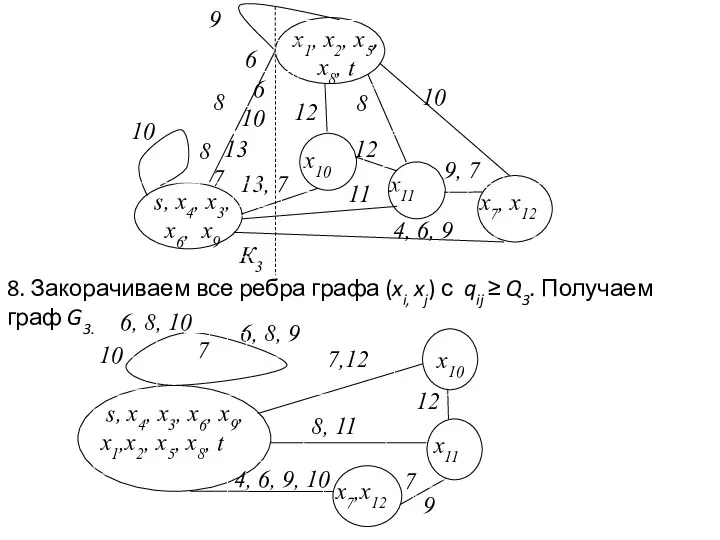
- 25. 8. Закорачиваем все ребра графа (xi, xj) с qij ≥ Q3. Получаем граф G3.
- 27. Скачать презентацию










![6. l(xi*) = min[l(xi)] = l(x3) = 5. 7. l(x3)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/598287/slide-15.jpg)
![12. l(xi*) = min[l(xi)] = l(x7) = 11. 13. l(x7)](/_ipx/f_webp&q_80&fit_contain&s_1440x1080/imagesDir/jpg/598287/slide-16.jpg)



 Понятие, задачи корреляционно-регрессионного анализа и моделирования
Понятие, задачи корреляционно-регрессионного анализа и моделирования Сложение и вычитание положительных и отрицательных чисел
Сложение и вычитание положительных и отрицательных чисел Тригонометрические формулы. 10 класс
Тригонометрические формулы. 10 класс Модуль числа
Модуль числа Плоскость. Задание плоскости на чертеже. Точка и прямая в плоскости
Плоскость. Задание плоскости на чертеже. Точка и прямая в плоскости Сложение натуральных чисел и его свойства
Сложение натуральных чисел и его свойства Угол между скрещивающимися прямыми
Угол между скрещивающимися прямыми Урок алгебры в 7 классе Разложение многочленов на множители
Урок алгебры в 7 классе Разложение многочленов на множители Алгебраические выражения
Алгебраические выражения В стране занимательной математики
В стране занимательной математики Закрепление по теме : Нумерация чисел больше 1000.в 4 классе
Закрепление по теме : Нумерация чисел больше 1000.в 4 классе Презентация игры Собери неделю для старшей группы
Презентация игры Собери неделю для старшей группы Арифметикалық және геометриялық прогрессияларды есептер шығаруда қолдану
Арифметикалық және геометриялық прогрессияларды есептер шығаруда қолдану Сравнение по модулю m
Сравнение по модулю m Проверка сложения во 2 классе
Проверка сложения во 2 классе Применение ЭОР и ИКТ на уроках математики в рамках реализации ФГОС (презентация материалов из опыта работы)
Применение ЭОР и ИКТ на уроках математики в рамках реализации ФГОС (презентация материалов из опыта работы) Вычитание вида 14- ,15-
Вычитание вида 14- ,15- Это загадочное число Пи
Это загадочное число Пи Виды треугольников
Виды треугольников Презентация Времена года
Презентация Времена года Свойства действий с рациональными числами
Свойства действий с рациональными числами Методическая разработка - технологическая карта урока математики в 3 классе по теме Проверка умножения. ФГОС
Методическая разработка - технологическая карта урока математики в 3 классе по теме Проверка умножения. ФГОС Окружность, вписанная в правильный многоугольник
Окружность, вписанная в правильный многоугольник Статистические гипотезы
Статистические гипотезы Логарифмические уравнения
Логарифмические уравнения Сравнение десятичных дробей
Сравнение десятичных дробей Геометрические задачи С2, по материалам ЕГЭ
Геометрические задачи С2, по материалам ЕГЭ Решение задач в два действия
Решение задач в два действия