Содержание
- 2. 02 Разбиение Используется для разделения системы на меньшие подсистемы Обычно производится иерархически Система бьется до тех
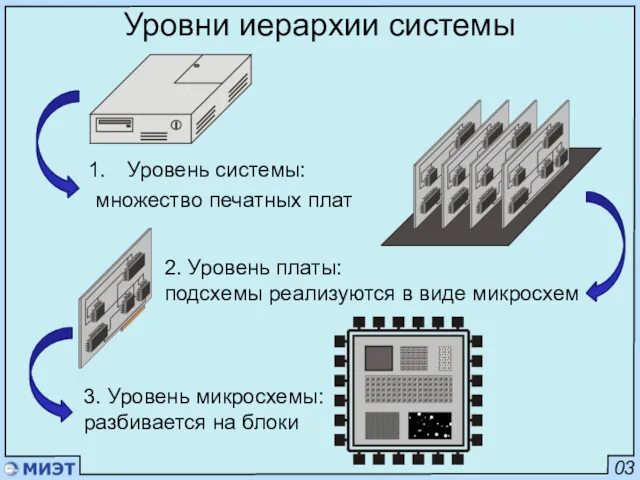
- 3. 03 Уровни иерархии системы Уровень системы: множество печатных плат 2. Уровень платы: подсхемы реализуются в виде
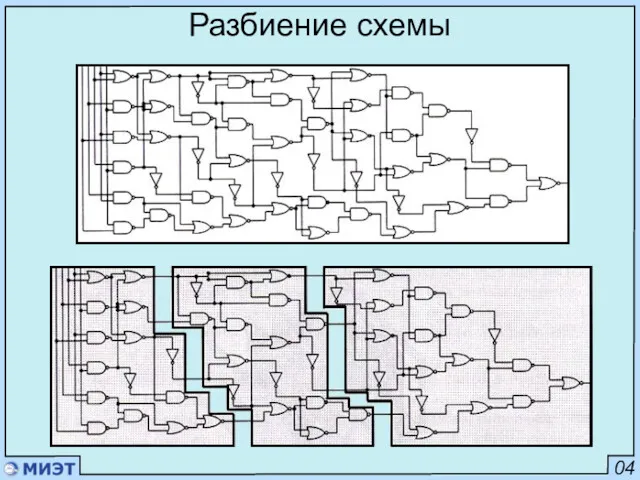
- 4. 04 Разбиение схемы
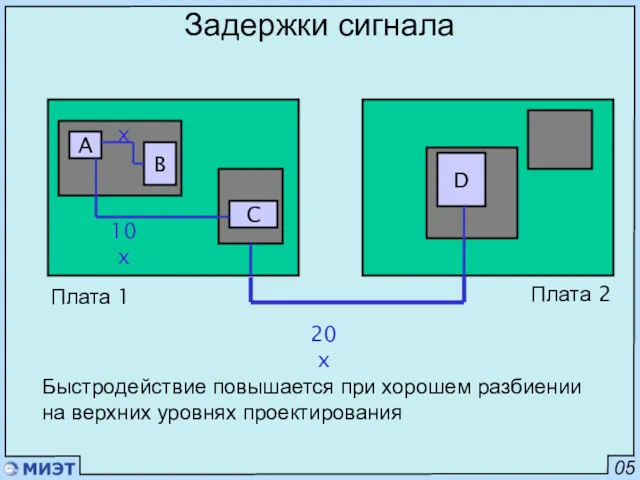
- 5. 05 Задержки сигнала Быстродействие повышается при хорошем разбиении на верхних уровнях проектирования A B C Плата
- 6. 06 Почему важна декомпозиция Стратегия «разделяй и властвуй» Эффективна для решения очень сложных задач Области применения:
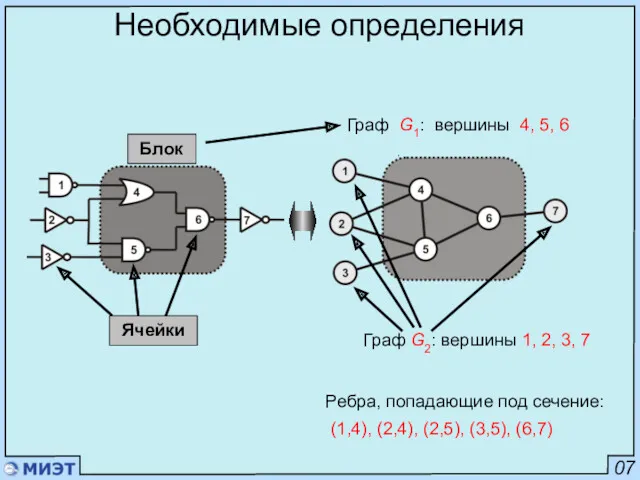
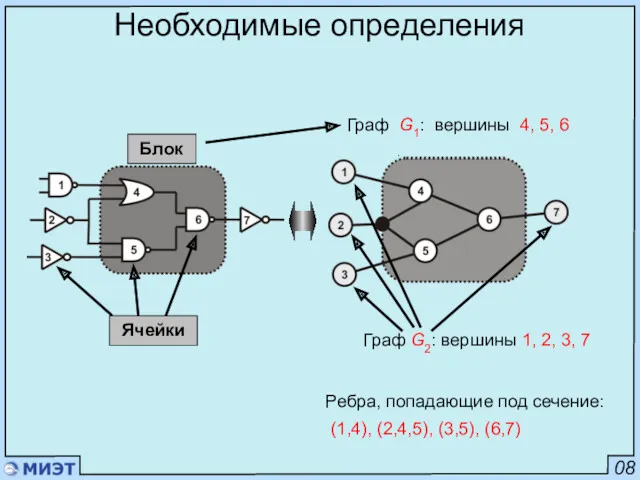
- 7. 07 Необходимые определения Блок Граф G2: вершины 1, 2, 3, 7 Граф G1: вершины 4, 5,
- 8. 08 Необходимые определения Блок Граф G2: вершины 1, 2, 3, 7 Граф G1: вершины 4, 5,
- 9. 09 Необходимые определения Декомпозиция: разбиение больших схем на несколько меньших сверху-вниз Кластеризация: группирование небольших элементов в
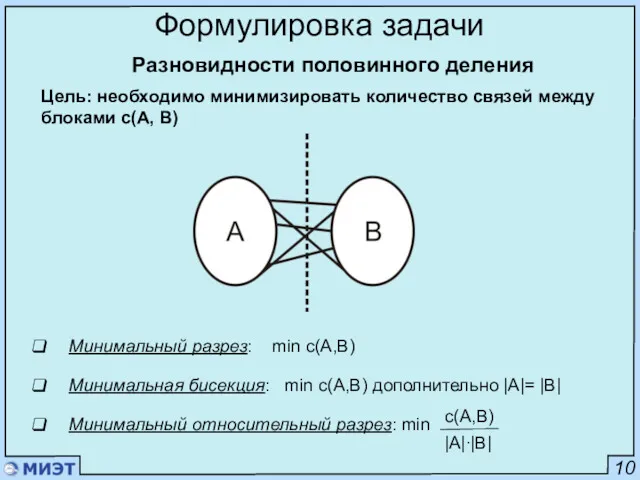
- 10. 10 Формулировка задачи Минимальный разрез: min c(А,B) Минимальная бисекция: min c(A,B) дополнительно |A|= |B| Минимальный относительный
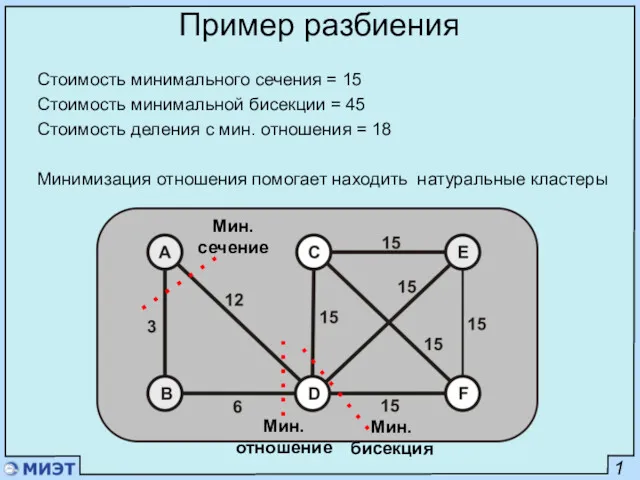
- 11. 11 Пример разбиения Стоимость минимального сечения = 15 Стоимость минимальной бисекции = 45 Стоимость деления с
- 12. 12 Критерии и ограничения Критерии: минимальная связанность блоков максимальная связанность блоков равномерная связанность блоков функциональный признак
- 13. 13 Классификация алгоритмов Улучшают начальное разбиение Наиболее распространены из-за эффективности Алгоритмы декомпозиции Конструктивные Итерационные Классы алгоритмов
- 14. 14 Классификация алгоритмов Производят различные решения при каждом запуске Алгоритмы декомпозиции Детерминистические Вероятностные Классы алгоритмов декомпозиции
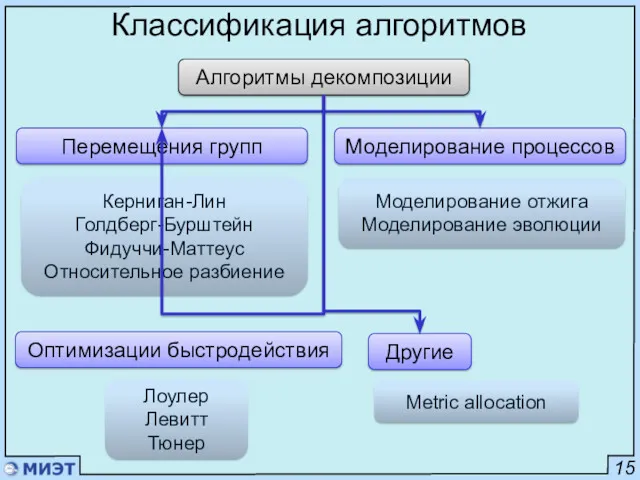
- 15. 15 Классификация алгоритмов Перемещения групп Керниган-Лин Голдберг-Бурштейн Фидуччи-Маттеус Относительное разбиение Моделирование процессов Оптимизации быстродействия Другие Алгоритмы
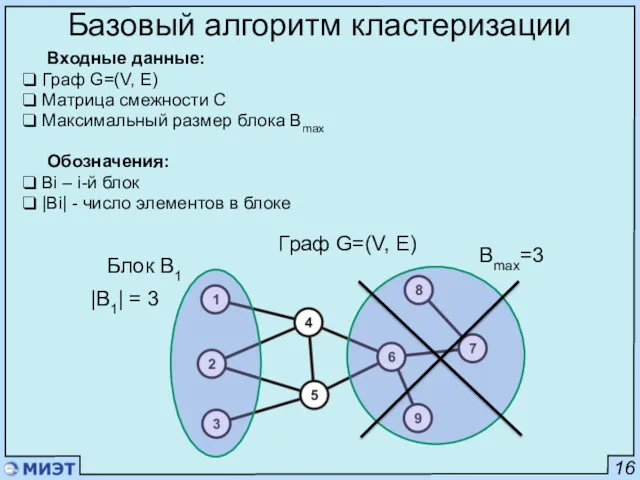
- 16. 16 Базовый алгоритм кластеризации Входные данные: Граф G=(V, E) Матрица смежности С Максимальный размер блока Bmax
- 17. 17 Базовый алгоритм кластеризации Алгоритм: i=1 Пока в Е есть элементы Если |Bi|=0 Найти элемент с
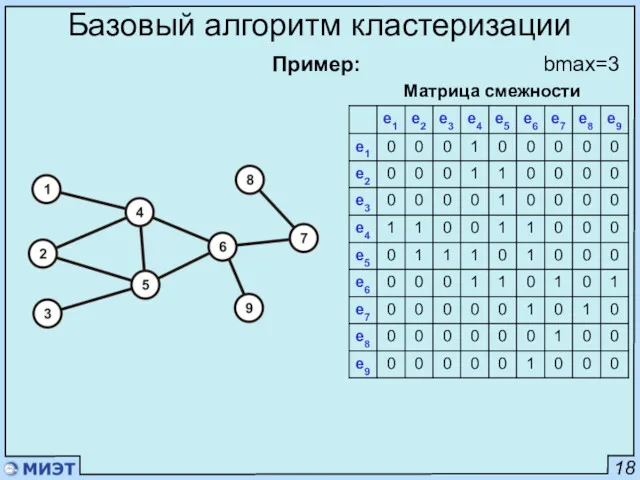
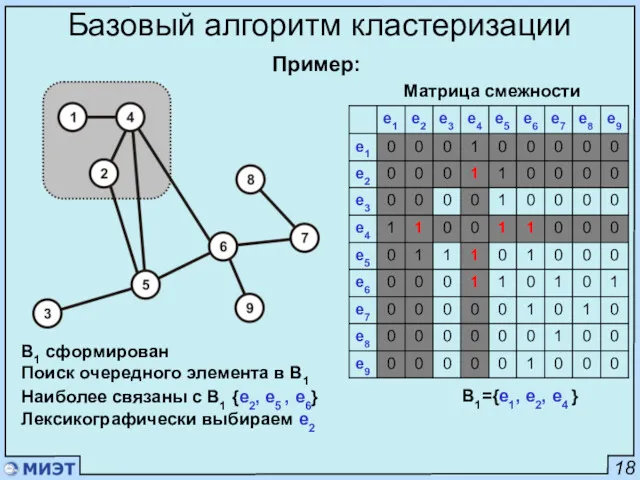
- 18. 18 Базовый алгоритм кластеризации Пример: Матрица смежности bmax=3
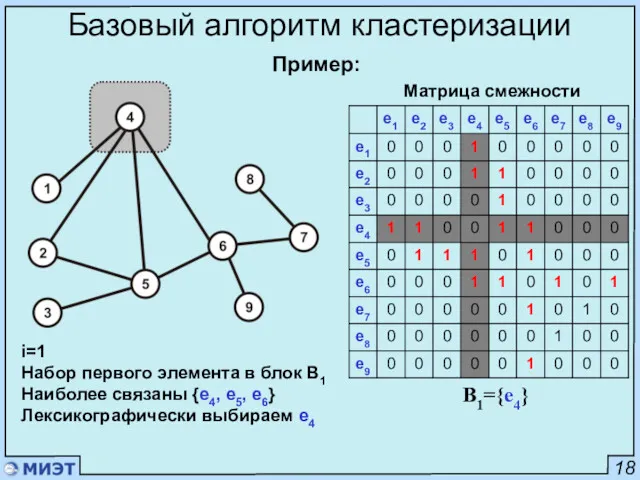
- 19. 18 Базовый алгоритм кластеризации Пример: Матрица смежности i=1 Набор первого элемента в блок B1 Наиболее связаны
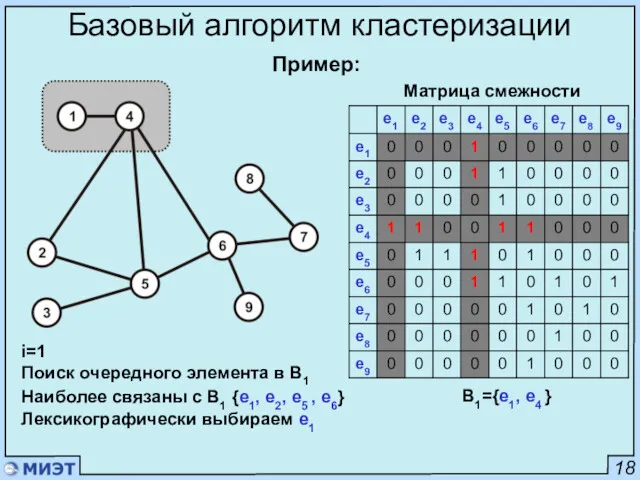
- 20. 18 Базовый алгоритм кластеризации Пример: Матрица смежности i=1 Поиск очередного элемента в B1 Наиболее связаны с
- 21. 18 Базовый алгоритм кластеризации Пример: Матрица смежности B1 сформирован Поиск очередного элемента в B1 Наиболее связаны
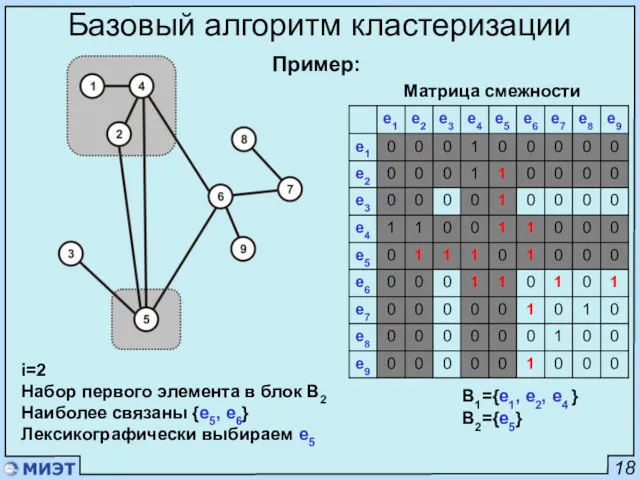
- 22. 18 Базовый алгоритм кластеризации Матрица смежности i=2 Набор первого элемента в блок B2 Наиболее связаны {e5,
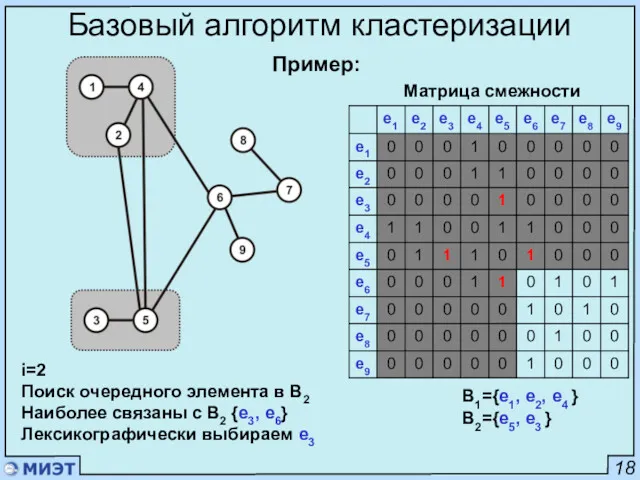
- 23. 18 Базовый алгоритм кластеризации Матрица смежности i=2 Поиск очередного элемента в B2 Наиболее связаны с B2
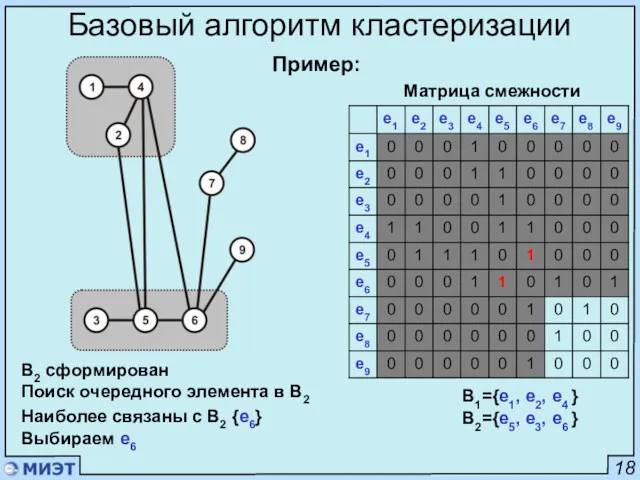
- 24. 18 Базовый алгоритм кластеризации Матрица смежности B2 сформирован Поиск очередного элемента в B2 Наиболее связаны с
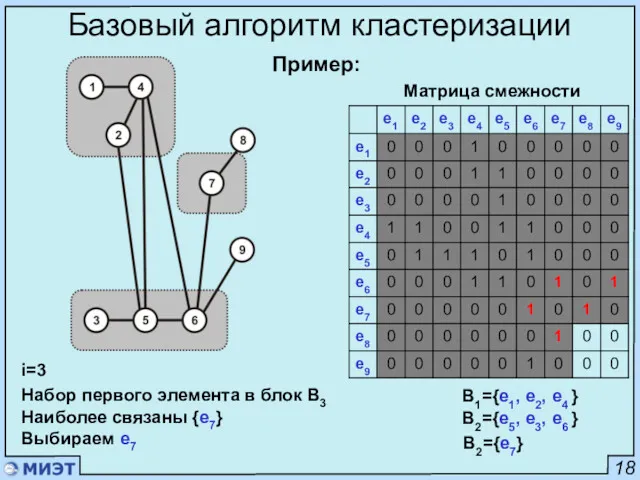
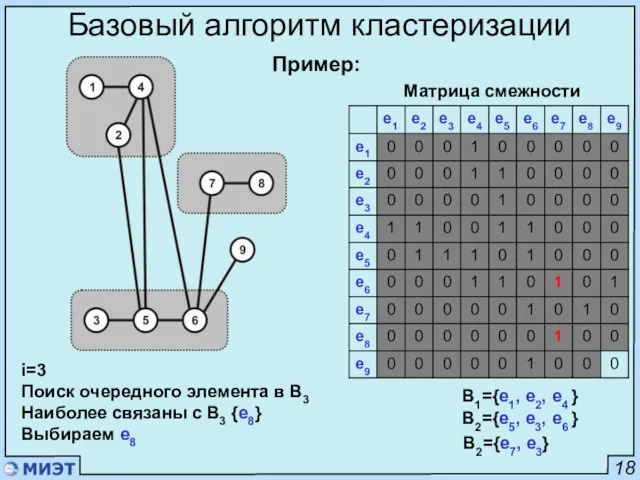
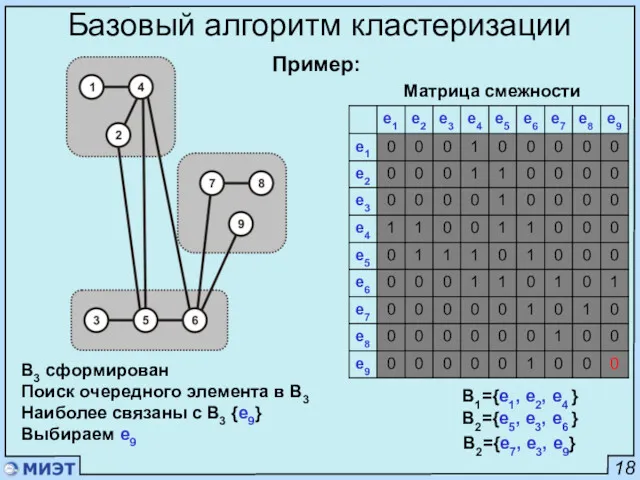
- 25. 18 Базовый алгоритм кластеризации Матрица смежности i=3 Набор первого элемента в блок B3 Наиболее связаны {e7}
- 26. 18 Базовый алгоритм кластеризации Матрица смежности B1={e1, e2, e4 } B2={e5, e3, e6 } B2={e7, e3}
- 27. 18 Базовый алгоритм кластеризации Матрица смежности B1={e1, e2, e4 } B2={e5, e3, e6 } B2={e7, e3,
- 28. 19 Базовый алгоритм кластеризации Способы повышения эффективности: После переноса вершины в кластер обновлять матрицу смежности (не
- 29. 20 Алгоритм Кодреса Идеи алгоритма Блоки формируются последовательно Первый элемент блока выбирается по набольшей связности с
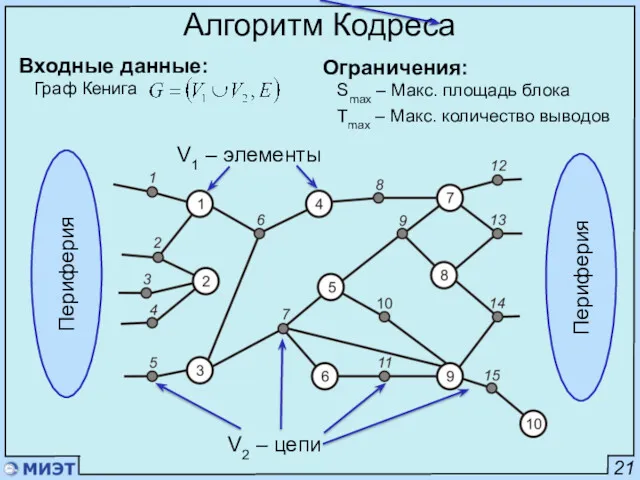
- 30. 21 Алгоритм Кодреса Входные данные: Граф Кенига . V1 – элементы Ограничения: Smax – Макс. площадь
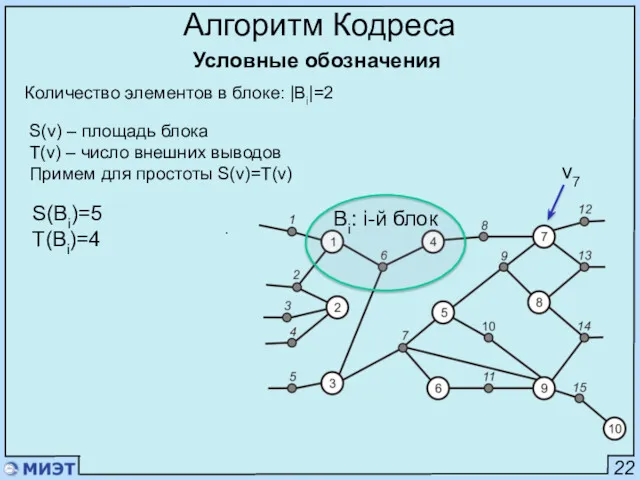
- 31. 22 Алгоритм Кодреса Условные обозначения . Bi: i-й блок Количество элементов в блоке: |Bi|=2 v7 S(v)
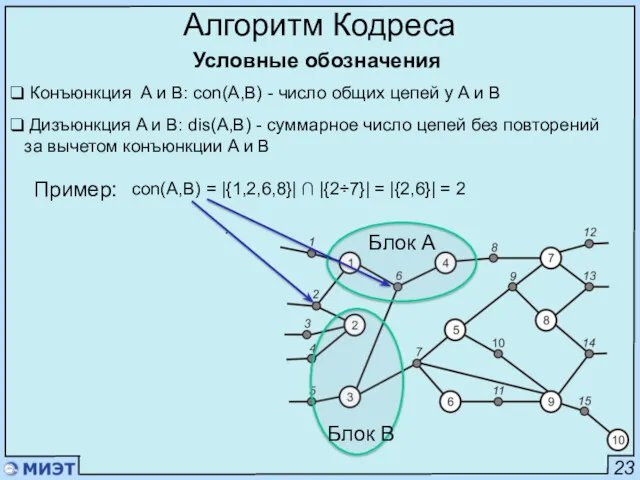
- 32. 23 Алгоритм Кодреса Условные обозначения . Блок А Конъюнкция A и B: con(A,B) - число общих
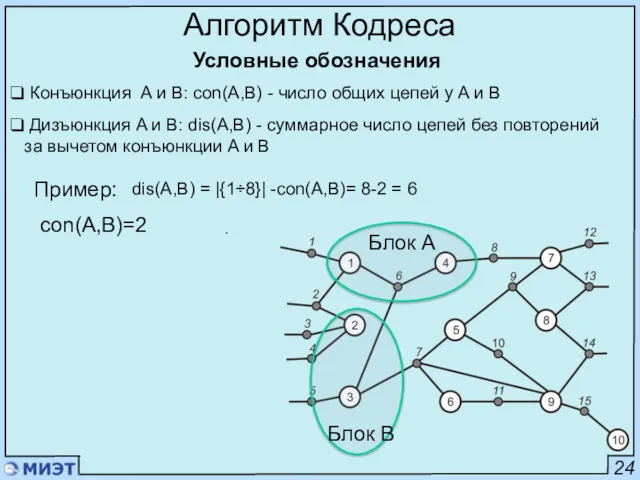
- 33. 24 Алгоритм Кодреса Условные обозначения . Блок А Конъюнкция A и B: con(A,B) - число общих
- 34. 25 Алгоритм Кодреса 1. i=1; A=A0 2. Выбрать a из A так, что Если есть равные,
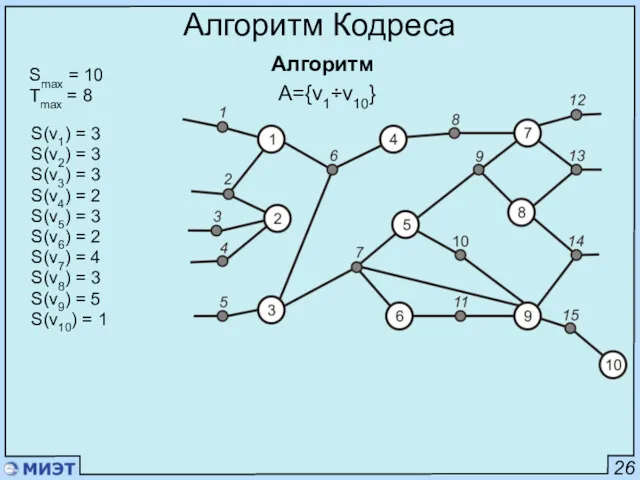
- 35. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 S(v1) = 3 S(v2) = 3
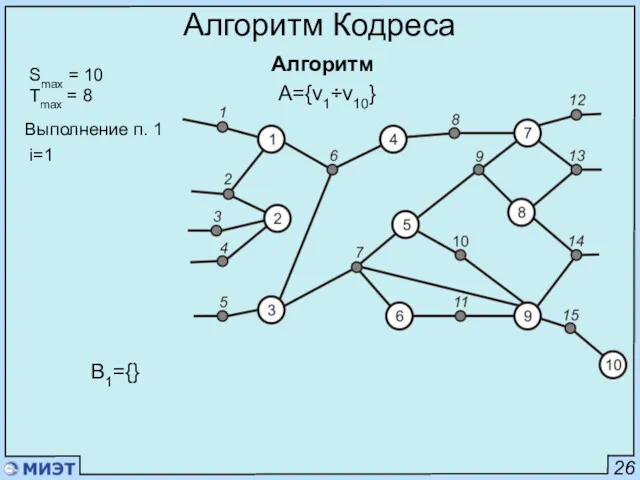
- 36. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 i=1 A={v1÷v10} B1={} Выполнение п. 1
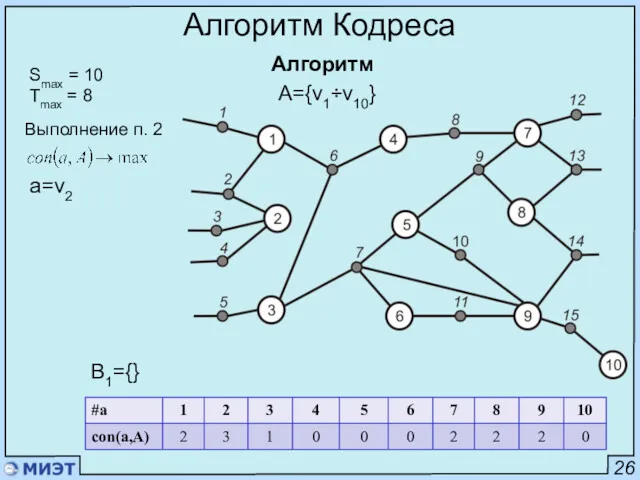
- 37. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} B1={} Выполнение п. 2 a=v2
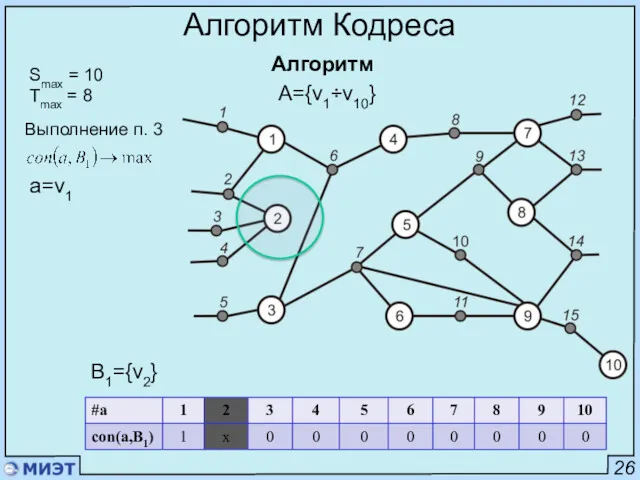
- 38. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} B1={v2} Выполнение п. 3 a=v1
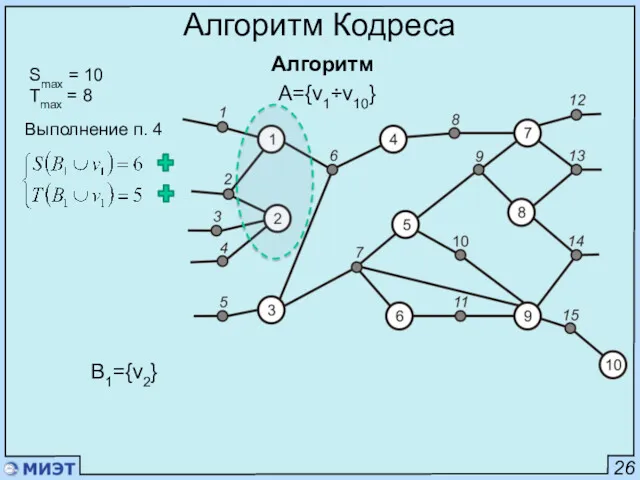
- 39. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} B1={v2} Выполнение п. 4
- 40. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} B1={v1, v2} Выполнение п. 3
- 41. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} B1={v1, v2} Выполнение п. 3
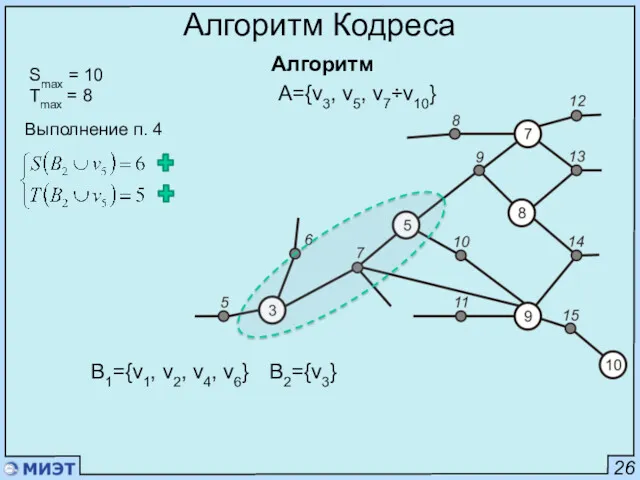
- 42. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} Выполнение п. 4 B1={v1, v2}
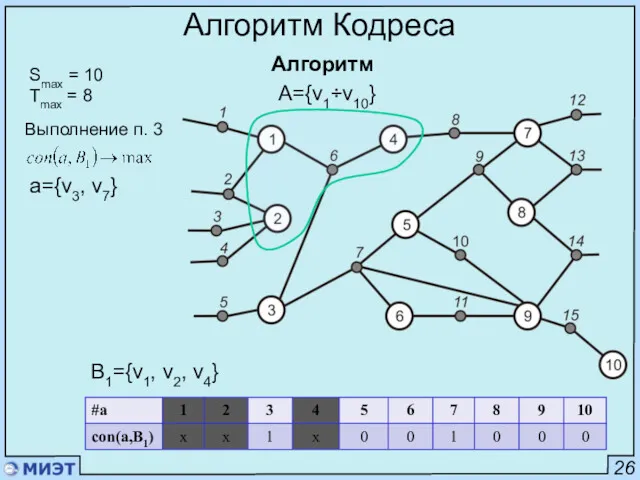
- 43. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} B1={v1, v2, v4} Выполнение п.
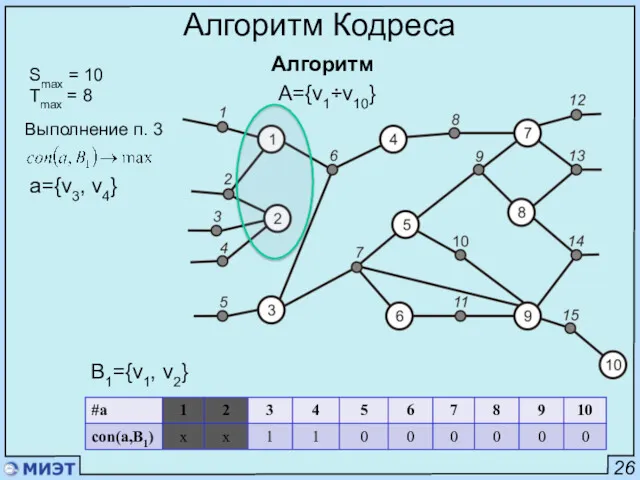
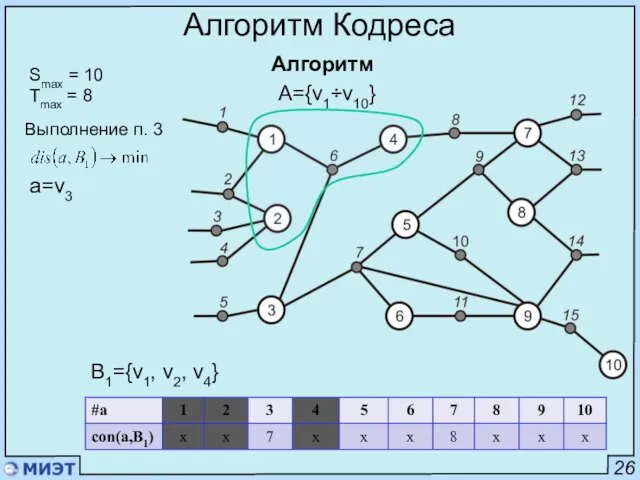
- 44. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} Выполнение п. 3 a=v3 B1={v1,
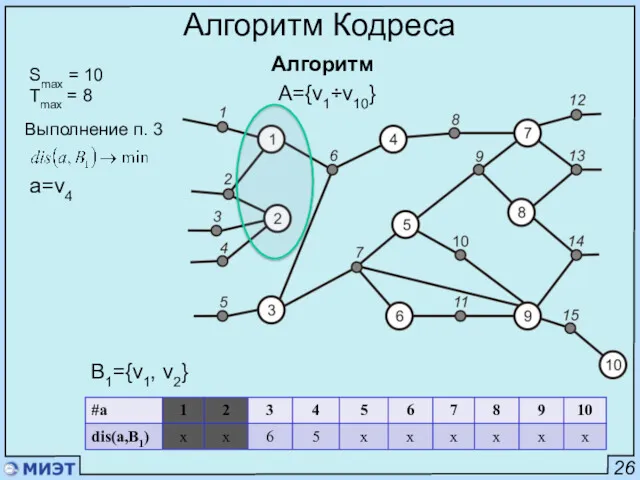
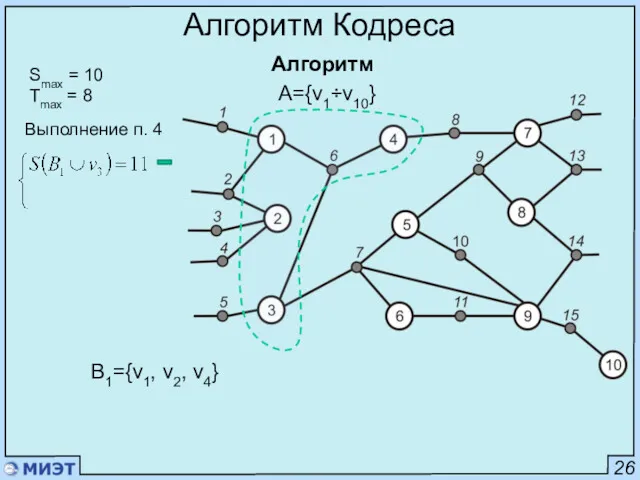
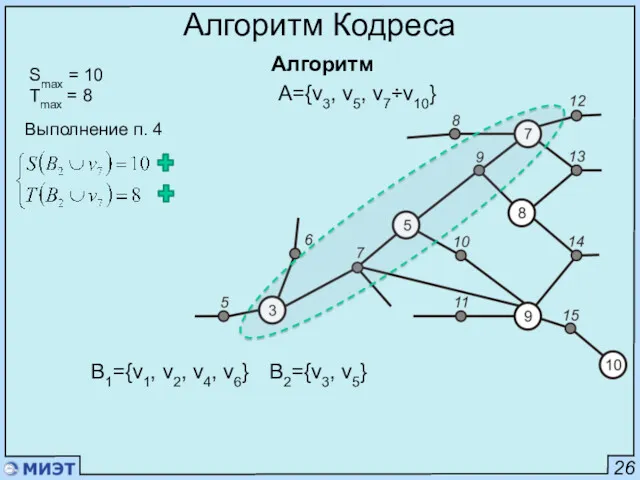
- 45. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} Выполнение п. 4 B1={v1, v2,
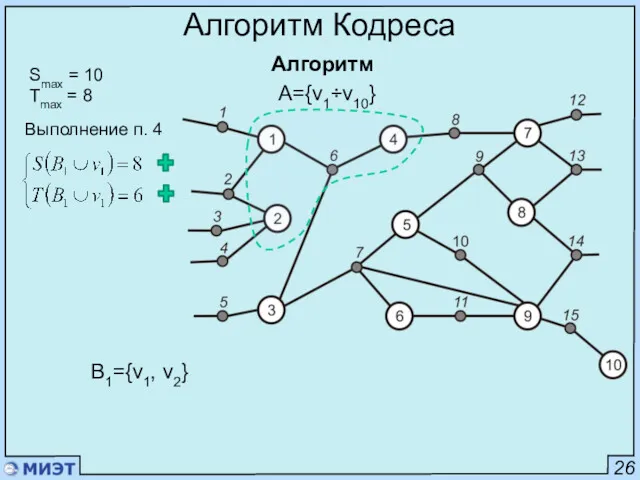
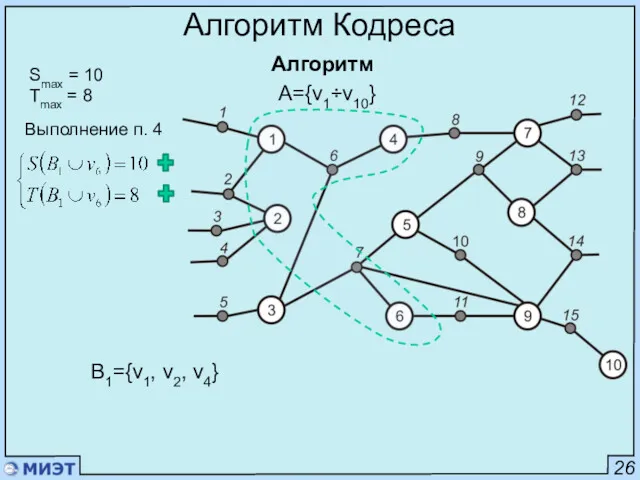
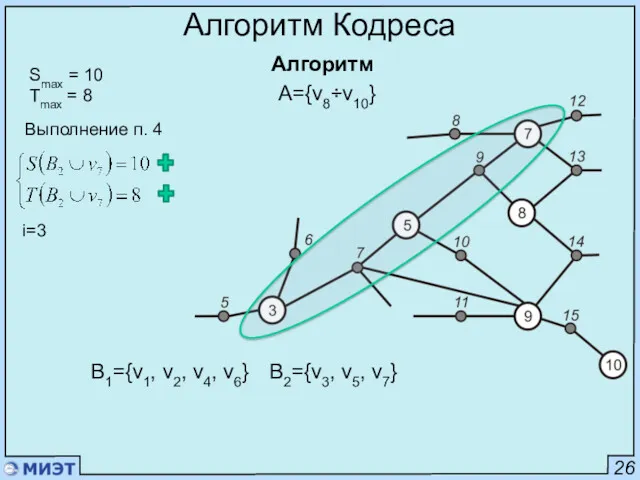
- 46. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 A={v1÷v10} Выполнение п. 4 B1={v1, v2,
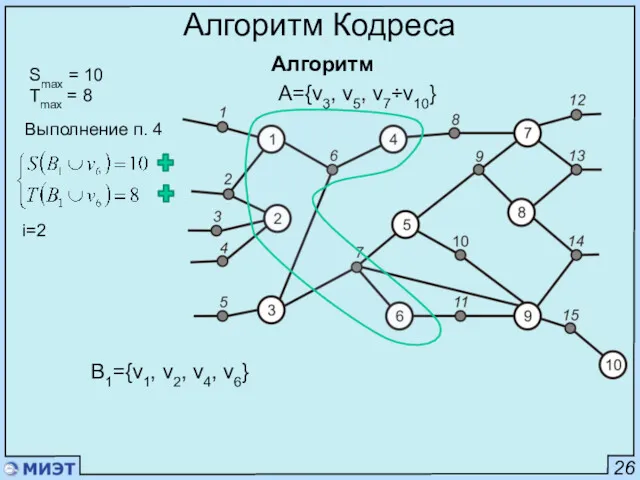
- 47. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 4 B1={v1, v2, v4,
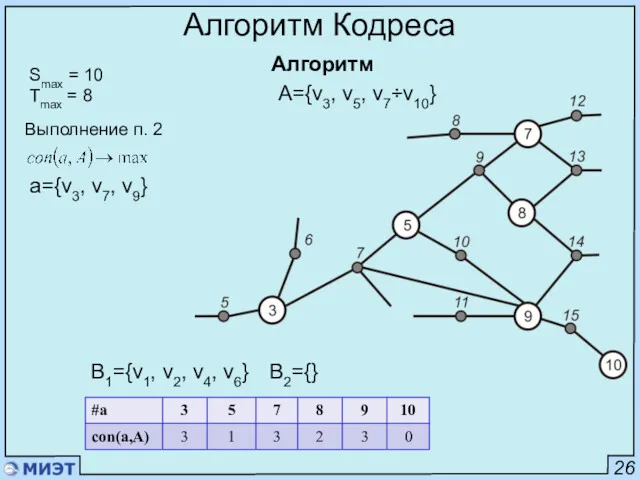
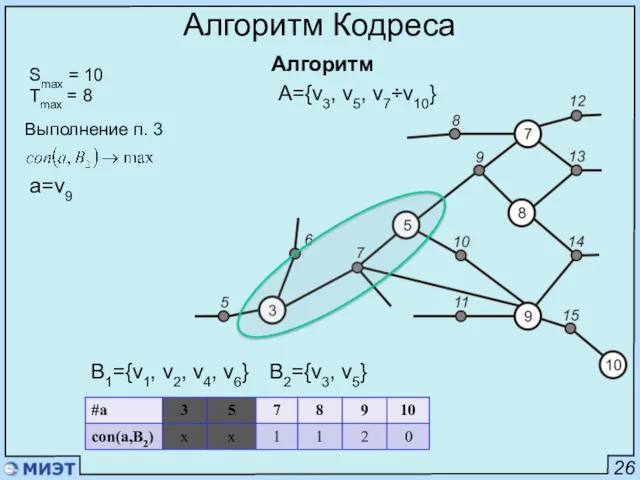
- 48. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 2 a={v3, v7, v9}
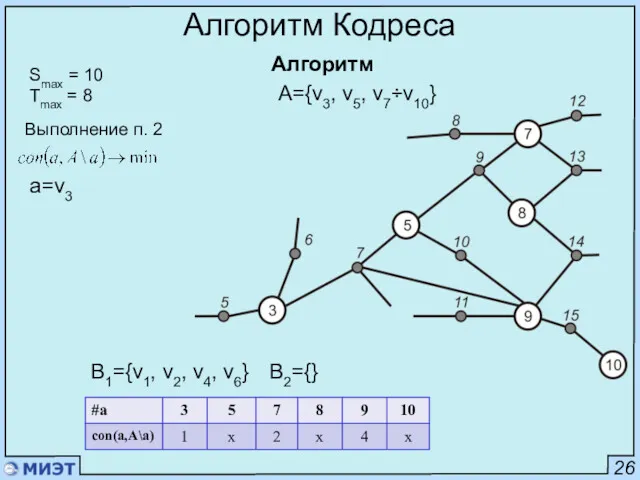
- 49. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 2 a=v3 B2={} B1={v1,
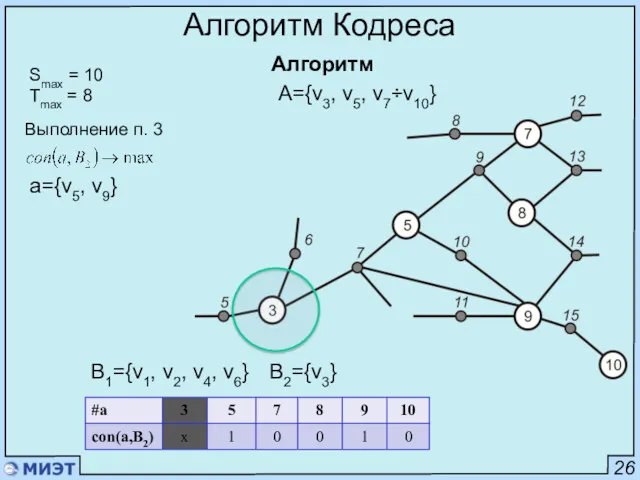
- 50. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 3 a={v5, v9} B1={v1,
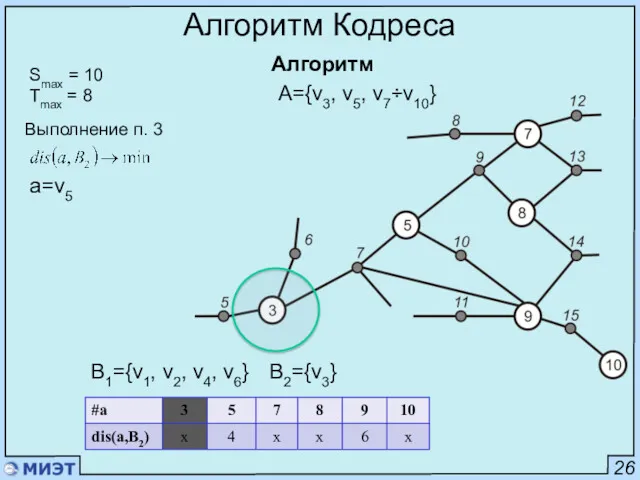
- 51. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 3 a=v5 B1={v1, v2,
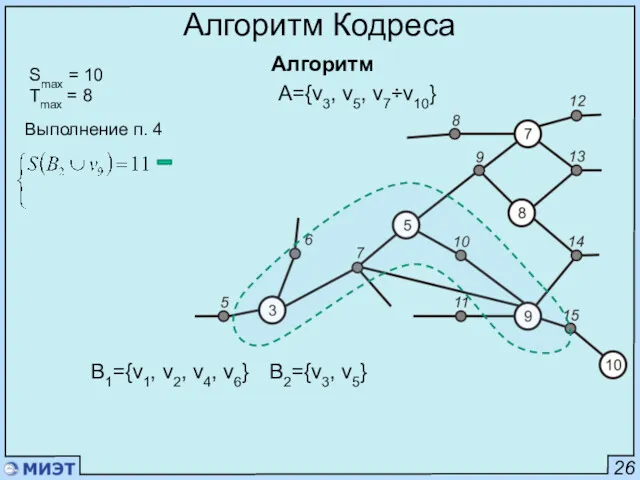
- 52. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 4 B1={v1, v2, v4,
- 53. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 B1={v1, v2, v4, v6} B2={v3, v5}
- 54. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 B1={v1, v2, v4, v6} B2={v3, v5}
- 55. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 B1={v1, v2, v4, v6} B2={v3, v5}
- 56. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 B1={v1, v2, v4, v6} B2={v3, v5,
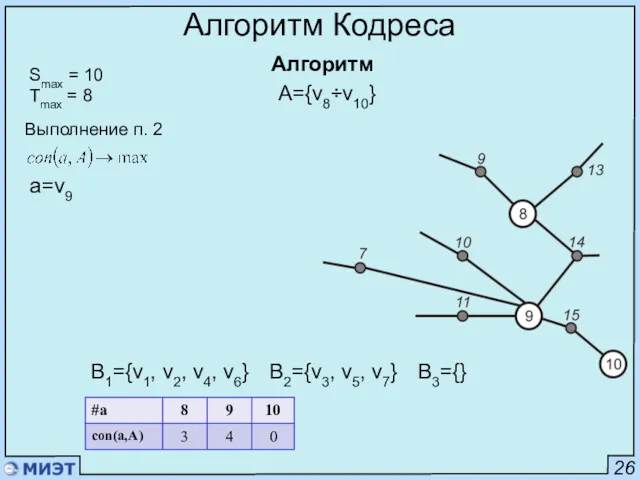
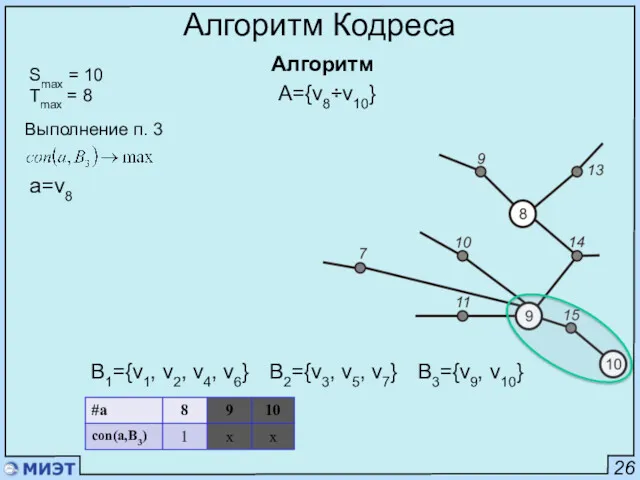
- 57. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 2 a=v9 A={v8÷v10} B1={v1,
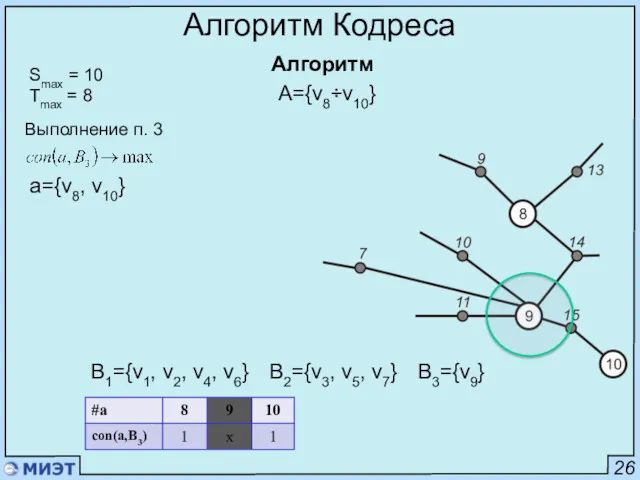
- 58. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 3 a={v8, v10} A={v8÷v10}
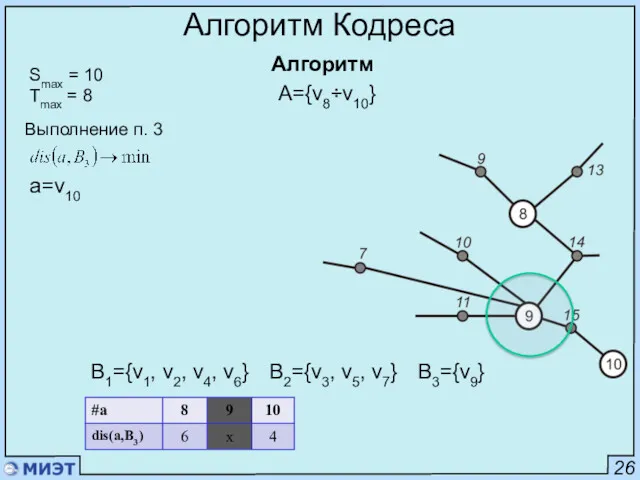
- 59. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 3 a=v10 A={v8÷v10} B1={v1,
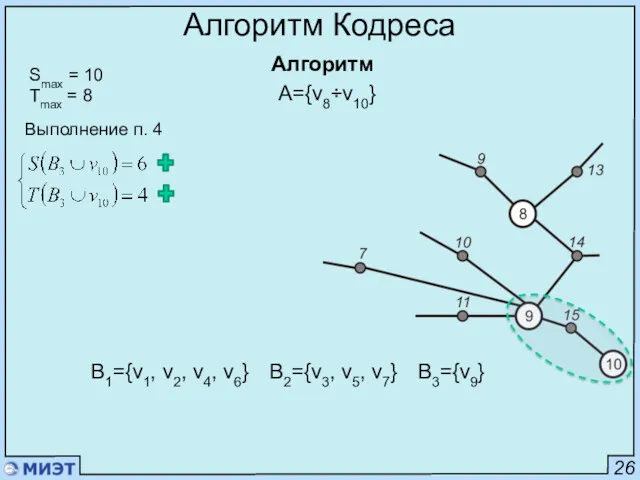
- 60. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 4 A={v8÷v10} B1={v1, v2,
- 61. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 3 a=v8 A={v8÷v10} B1={v1,
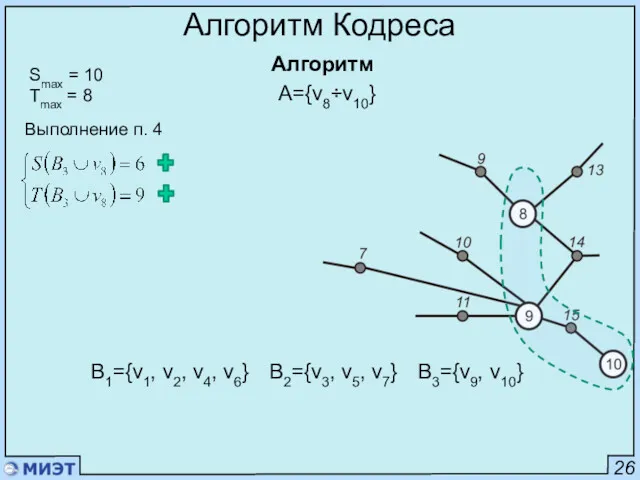
- 62. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 4 A={v8÷v10} B1={v1, v2,
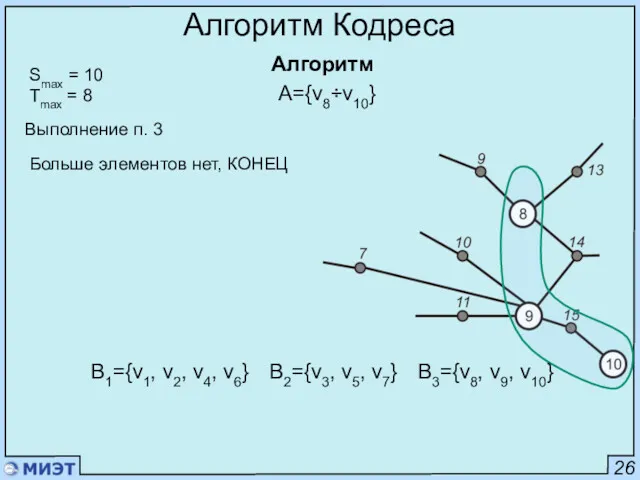
- 63. 26 Алгоритм Кодреса Алгоритм Smax = 10 Tmax = 8 Выполнение п. 3 A={v8÷v10} B1={v1, v2,
- 64. 27 Алгоритмы перемещения групп Принадлежат к итерационным алгоритмам Эти алгоритмы начинают работы с некоторого начального разбиения,
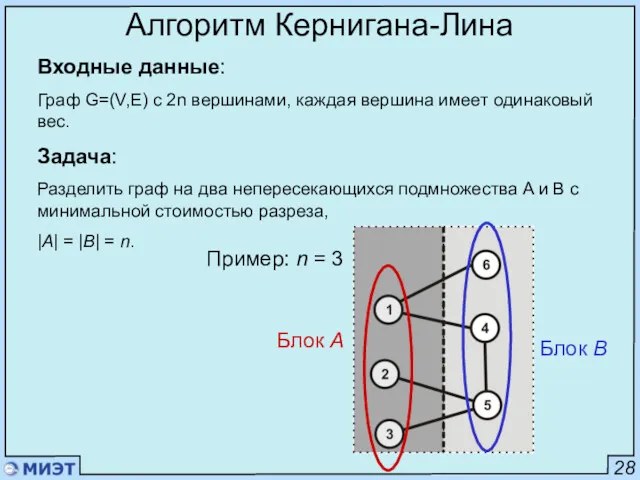
- 65. 28 Алгоритм Кернигана-Лина Входные данные: Граф G=(V,E) с 2n вершинами, каждая вершина имеет одинаковый вес. Задача:
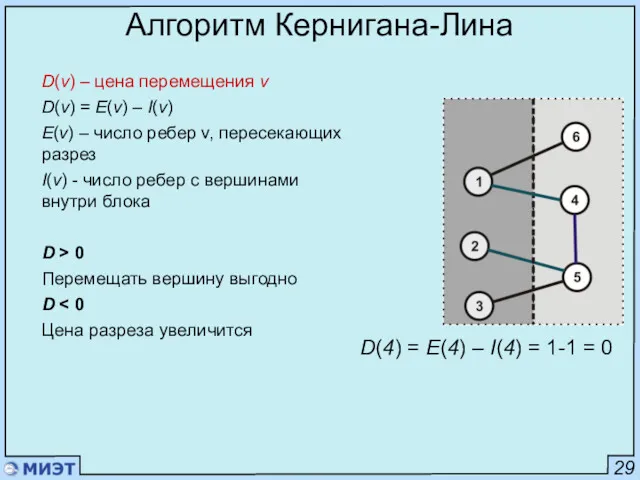
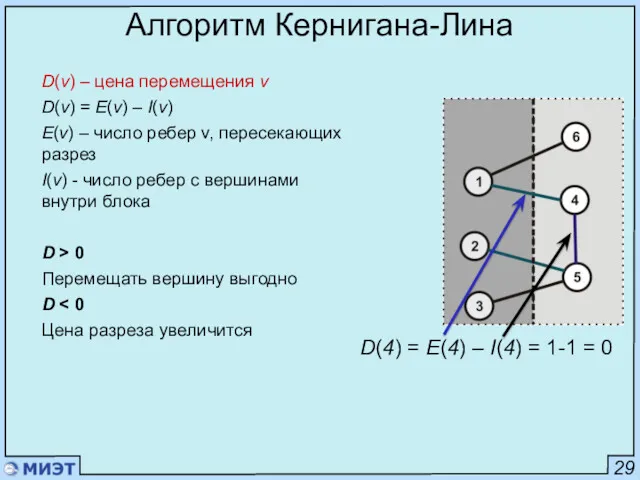
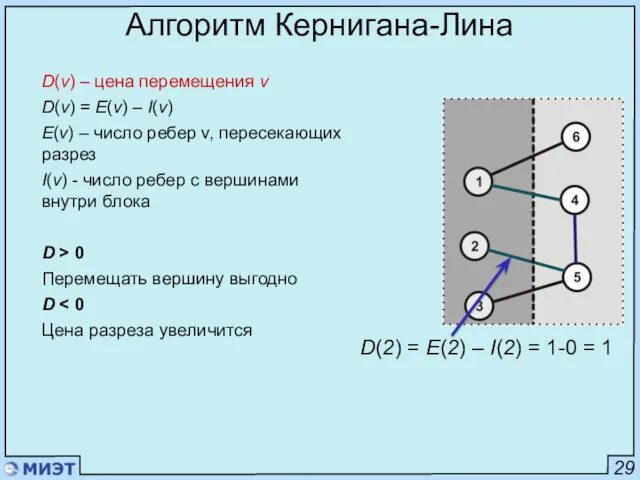
- 66. 29 Алгоритм Кернигана-Лина D(v) – цена перемещения v D(v) = E(v) – I(v) E(v) – число
- 67. 29 Алгоритм Кернигана-Лина D(v) – цена перемещения v D(v) = E(v) – I(v) E(v) – число
- 68. 29 Алгоритм Кернигана-Лина D(v) – цена перемещения v D(v) = E(v) – I(v) E(v) – число
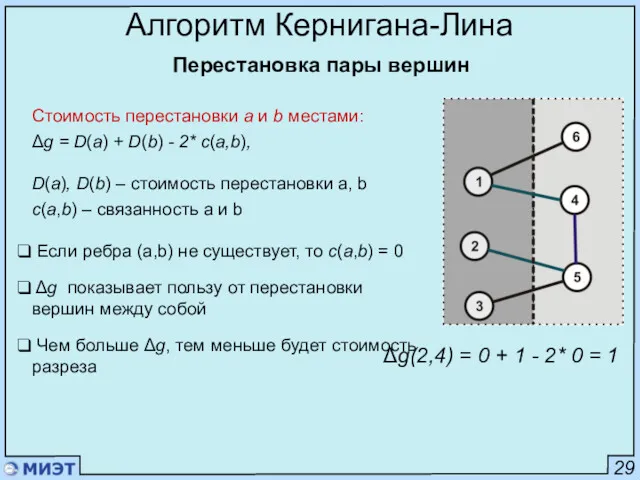
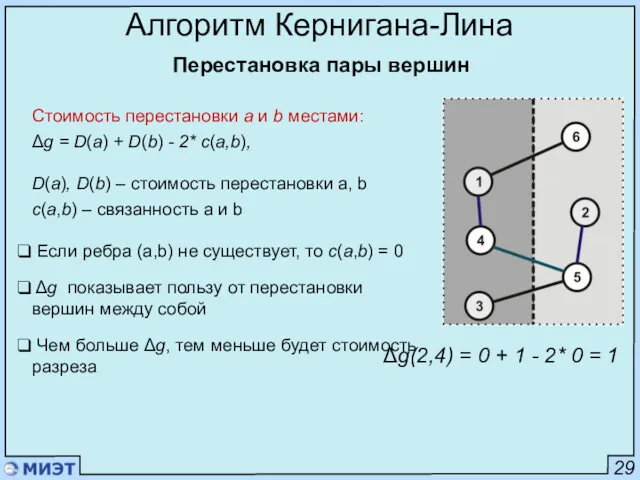
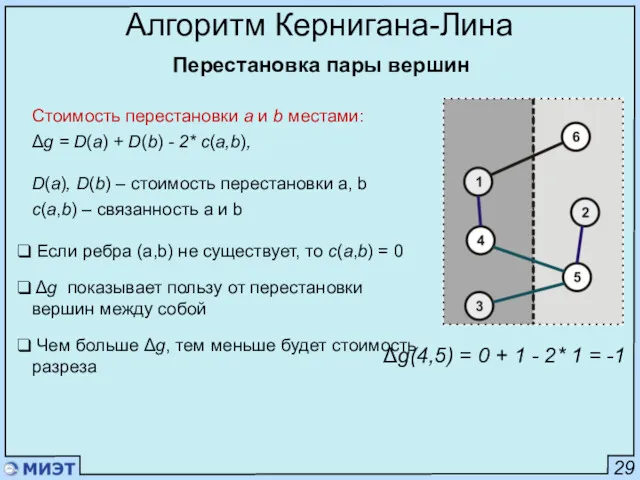
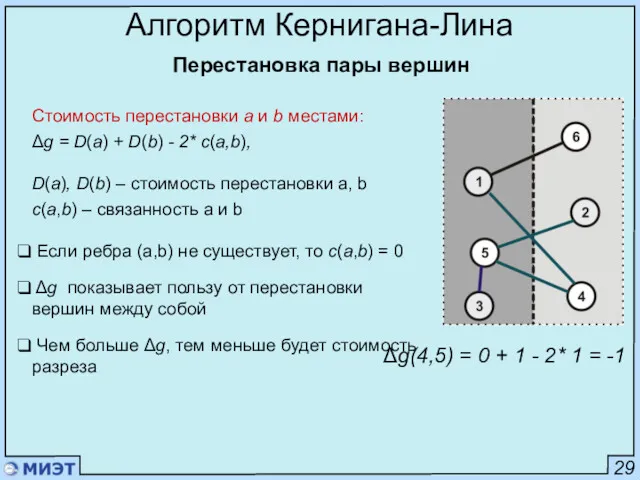
- 69. 29 Алгоритм Кернигана-Лина Стоимость перестановки a и b местами: Δg = D(a) + D(b) - 2*
- 70. 29 Алгоритм Кернигана-Лина Стоимость перестановки a и b местами: Δg = D(a) + D(b) - 2*
- 71. 29 Алгоритм Кернигана-Лина Стоимость перестановки a и b местами: Δg = D(a) + D(b) - 2*
- 72. 29 Алгоритм Кернигана-Лина Стоимость перестановки a и b местами: Δg = D(a) + D(b) - 2*
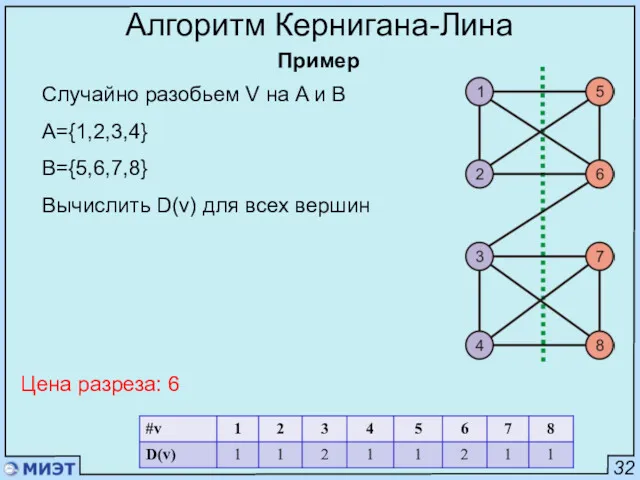
- 73. 30 Алгоритм Кернигана-Лина За один проход алгоритма необходимо максимизировать Gm Gm обо В конце прохода из
- 74. 31 Алгоритм Кернигана-Лина Алгоритм 1. Разбить V на A и B, |A|=|B|, A∩B=V 2. i=1 Вычислить
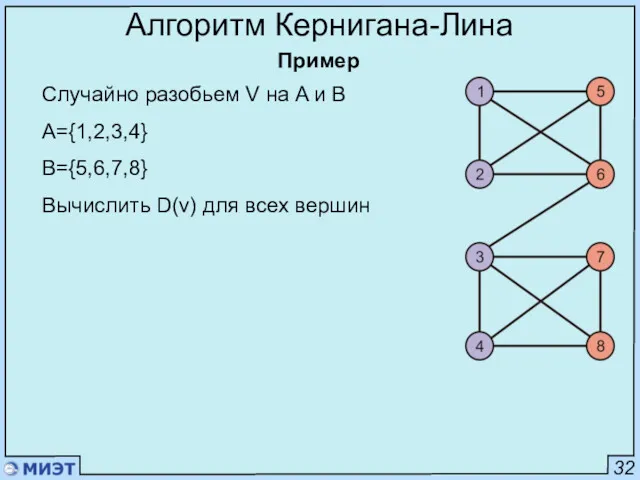
- 75. 32 Алгоритм Кернигана-Лина Пример Случайно разобьем V на A и B A={1,2,3,4} B={5,6,7,8} Вычислить D(v) для
- 76. 32 Алгоритм Кернигана-Лина Пример Случайно разобьем V на A и B A={1,2,3,4} B={5,6,7,8} Вычислить D(v) для
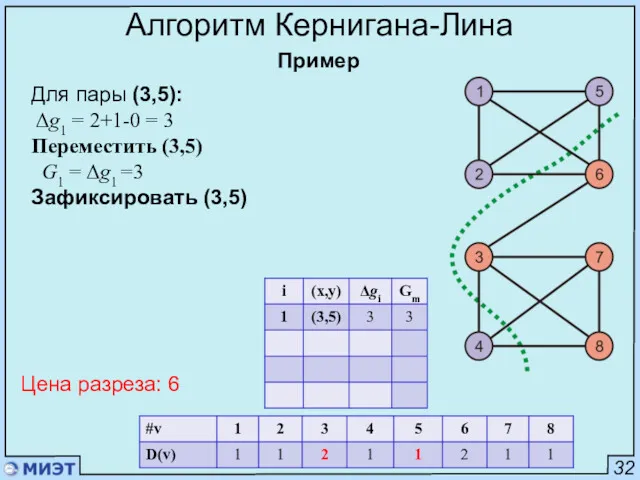
- 77. 32 Алгоритм Кернигана-Лина Пример Для пары (3,5): Δg1 = 2+1-0 = 3 Переместить (3,5) G1 =
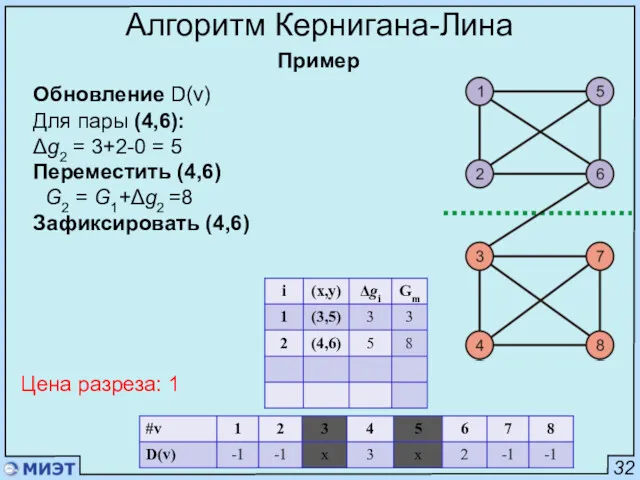
- 78. 32 Алгоритм Кернигана-Лина Пример Обновление D(v) Для пары (4,6): Δg2 = 3+2-0 = 5 Переместить (4,6)
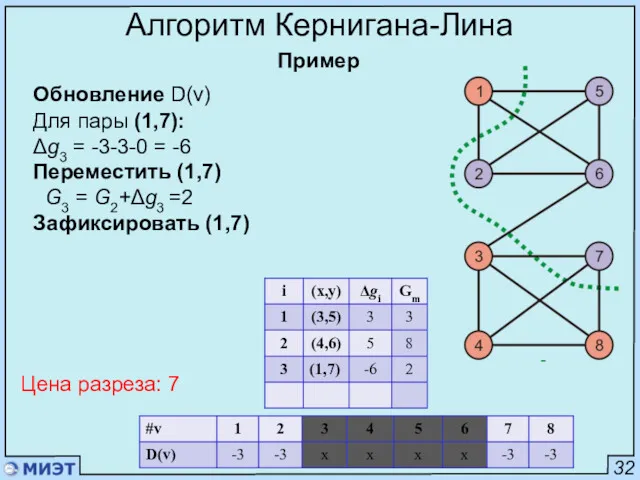
- 79. 32 Алгоритм Кернигана-Лина Пример Обновление D(v) Для пары (1,7): Δg3 = -3-3-0 = -6 Переместить (1,7)
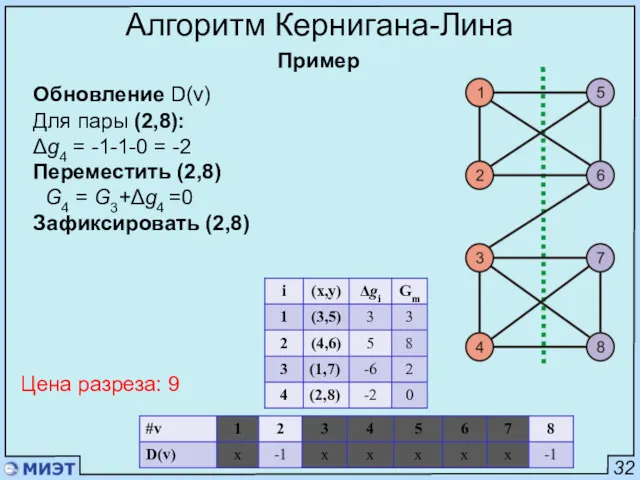
- 80. 32 Алгоритм Кернигана-Лина Пример Обновление D(v) Для пары (2,8): Δg4 = -1-1-0 = -2 Переместить (2,8)
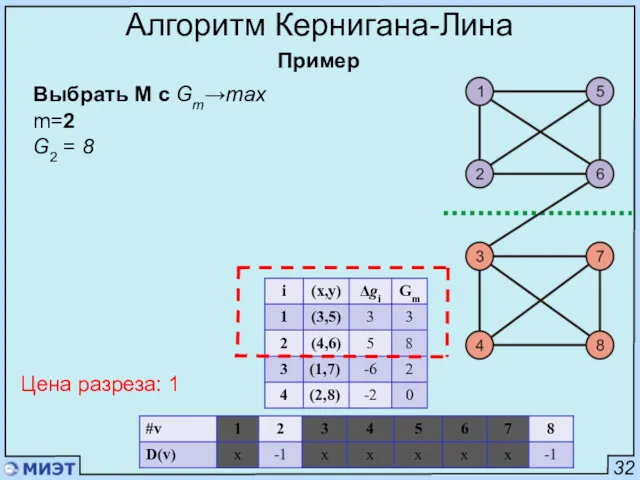
- 81. 32 Алгоритм Кернигана-Лина Пример Выбрать M c Gm→max m=2 G2 = 8 Цена разреза: 1
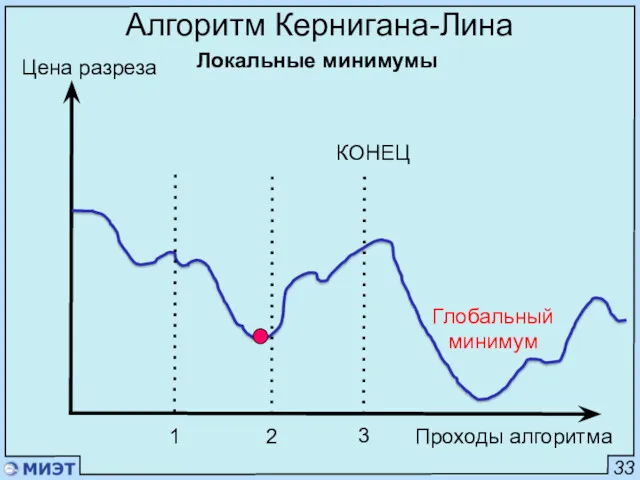
- 82. 33 Алгоритм Кернигана-Лина Проходы алгоритма Цена разреза Локальные минимумы КОНЕЦ 1 3 2 Глобальный минимум
- 83. 34 Анализ алгоритма Временная сложность: На каждый проход O(n2) при выборе лучшей пары Всего n/2 итераций
- 84. 35 Расширения алгоритма Перемещаются только одиночные вершины вместо пары Переделывается подсчет стоимости разреза для поддержки гиперребер
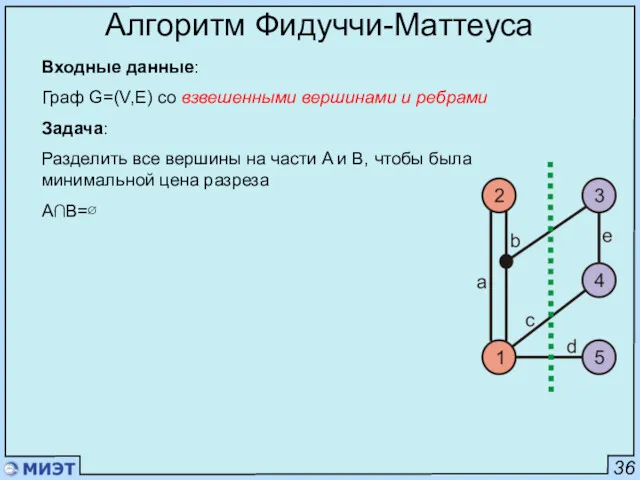
- 85. 36 Алгоритм Фидуччи-Маттеуса Входные данные: Граф G=(V,E) со взвешенными вершинами и ребрами Задача: Разделить все вершины
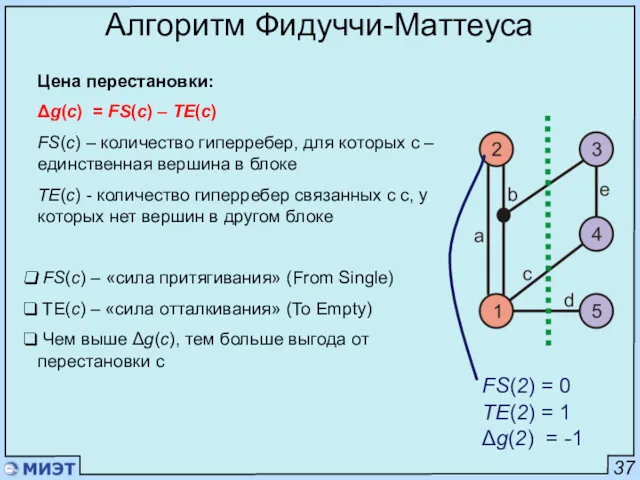
- 86. 37 Алгоритм Фидуччи-Маттеуса Цена перестановки: Δg(c) = FS(c) – TE(c) FS(c) – количество гиперребер, для которых
- 87. 38 Алгоритм Фидуччи-Маттеуса За один проход алгоритма необходимо максимизировать Gm Gm обо В конце прохода из
- 88. 39 Алгоритм Фидуччи-Маттеуса Критерий сбалансированности: Помогает сбалансировать размер блоков A и B Усовершенствует балансное соотношение Учитывает
- 89. 40 Алгоритм Фидуччи-Маттеуса Алгоритм 1. Рассчитать критерий сбалансированности 2. i=1 Вычислить Δgi для всех ячеек 3.
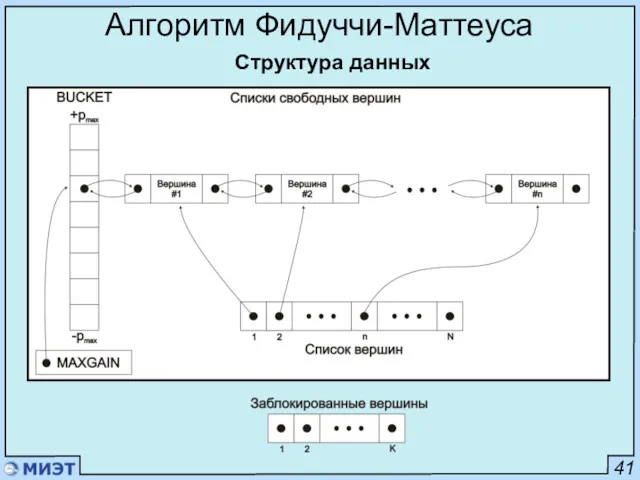
- 90. 41 Алгоритм Фидуччи-Маттеуса Структура данных
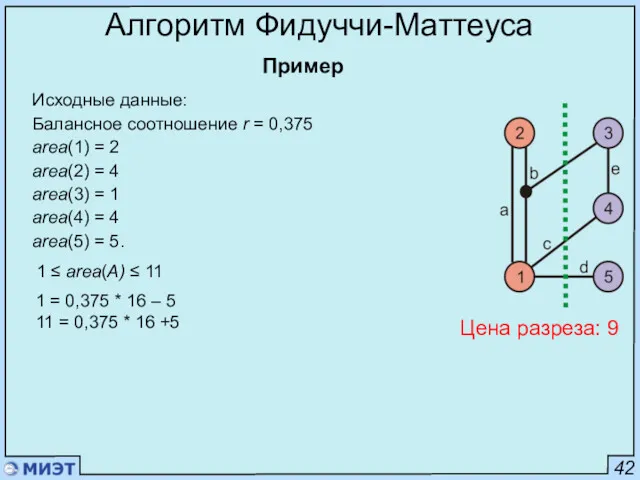
- 91. 42 Алгоритм Фидуччи-Маттеуса Пример Исходные данные: Балансное соотношение r = 0,375 area(1) = 2 area(2) =
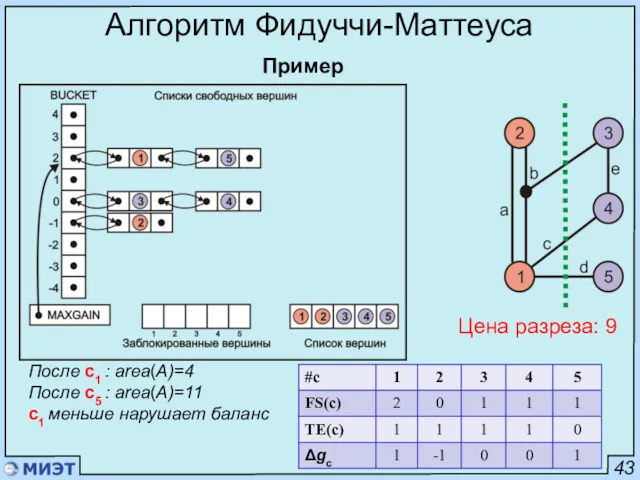
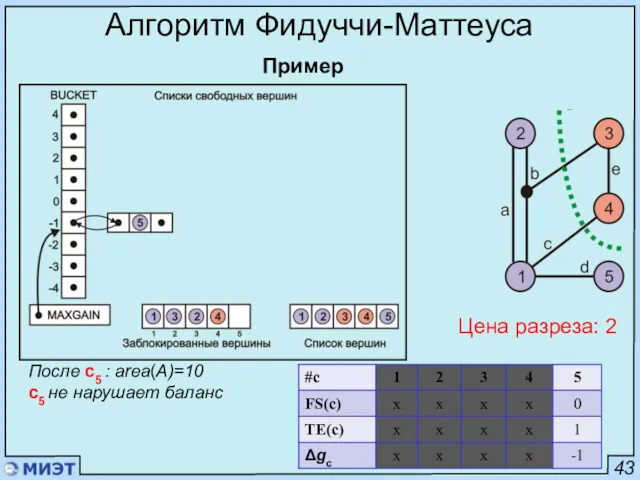
- 92. 43 Алгоритм Фидуччи-Маттеуса Пример Цена разреза: 9 После с1 : area(A)=4 После с5 : area(A)=11 с1
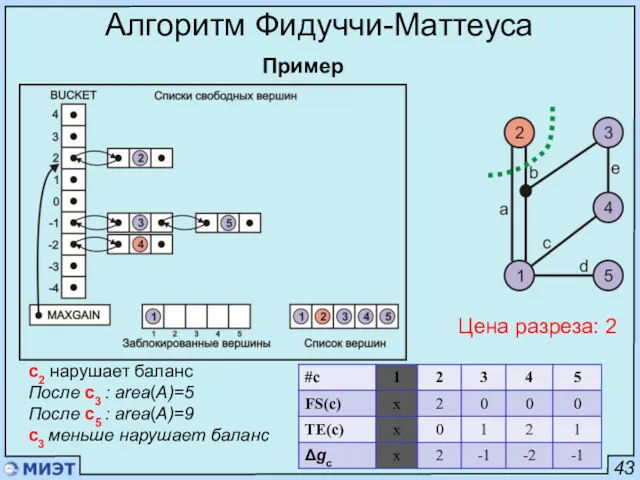
- 93. 43 Алгоритм Фидуччи-Маттеуса Пример Цена разреза: 2 с2 нарушает баланс После с3 : area(A)=5 После с5
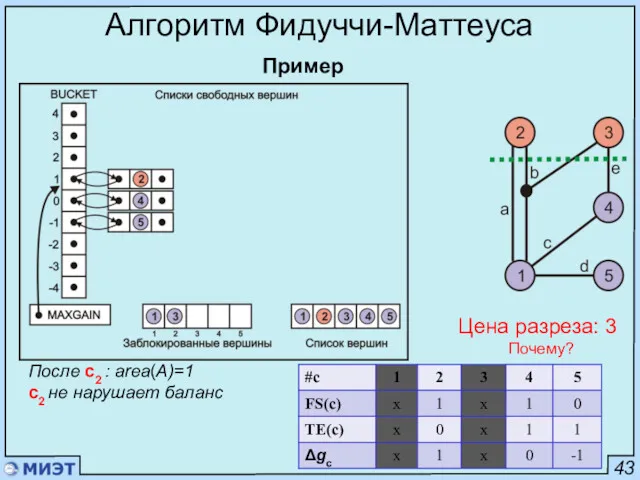
- 94. 43 Алгоритм Фидуччи-Маттеуса Пример Цена разреза: 3 Почему? После с2 : area(A)=1 с2 не нарушает баланс
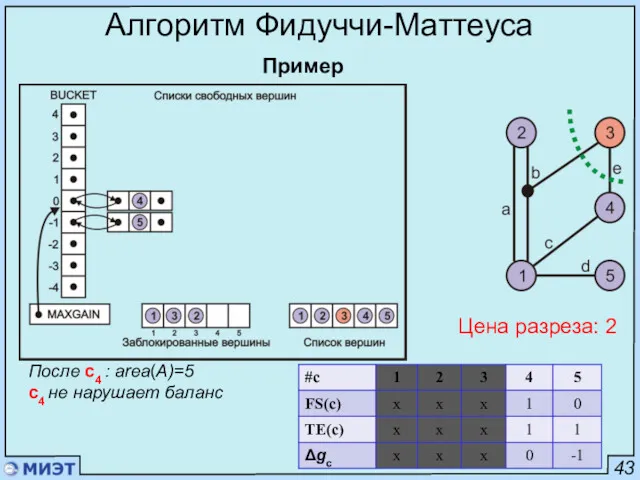
- 95. 43 Алгоритм Фидуччи-Маттеуса Пример Цена разреза: 2 После с4 : area(A)=5 с4 не нарушает баланс
- 96. 43 Алгоритм Фидуччи-Маттеуса Пример Цена разреза: 2 После с5 : area(A)=10 с5 не нарушает баланс
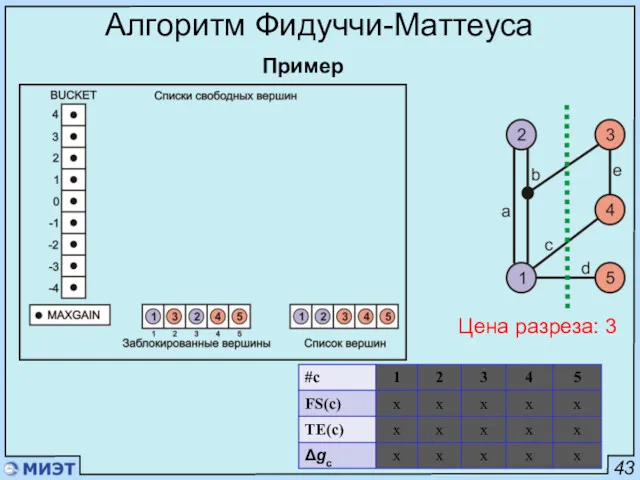
- 97. 43 Алгоритм Фидуччи-Маттеуса Пример Цена разреза: 3
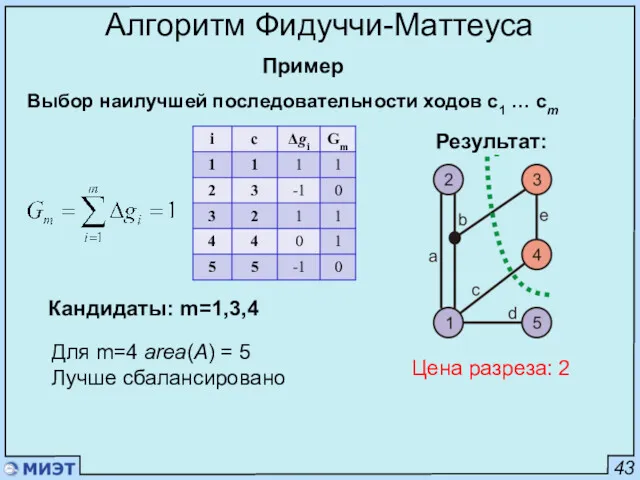
- 98. 43 Алгоритм Фидуччи-Маттеуса Пример Цена разреза: 2 Выбор наилучшей последовательности ходов c1 … cm Кандидаты: m=1,3,4
- 100. Скачать презентацию


















 Математика. 1 класс. Урок 75. Длина. Дециметр - Презентация
Математика. 1 класс. Урок 75. Длина. Дециметр - Презентация Меньше или больше. Демонстрационный материал. 5 класс
Меньше или больше. Демонстрационный материал. 5 класс Вписанные и центральные углы
Вписанные и центральные углы Линейная функция и ее график. 7 класс
Линейная функция и ее график. 7 класс Мода и медиана
Мода и медиана Поверхности второго порядка
Поверхности второго порядка Презентация по математике к уроку во 2 классе Замена двузначного числа суммой разрядных слагаемых Школа России
Презентация по математике к уроку во 2 классе Замена двузначного числа суммой разрядных слагаемых Школа России Задачи по планиметрии. ЕГЭ
Задачи по планиметрии. ЕГЭ Построение сечений многогранников методом следа
Построение сечений многогранников методом следа Составные задачи. Тренажёр (2 класс)
Составные задачи. Тренажёр (2 класс) Конспект открытого занятия в старшей группе: Интегрированное занятие по математике и развитию речи. Диск
Конспект открытого занятия в старшей группе: Интегрированное занятие по математике и развитию речи. Диск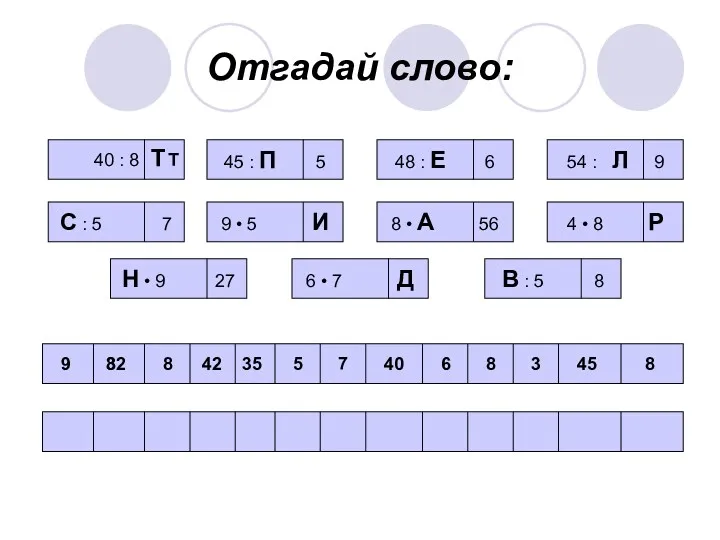 Презентация к уроку математики Повторение 3 класс
Презентация к уроку математики Повторение 3 класс Тренажёр Кот в сапогах (Математика, 1 класс)
Тренажёр Кот в сапогах (Математика, 1 класс) Решение задач с помощью уравнений
Решение задач с помощью уравнений Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения с разделяющимися переменными Формулы сокращенного умножения
Формулы сокращенного умножения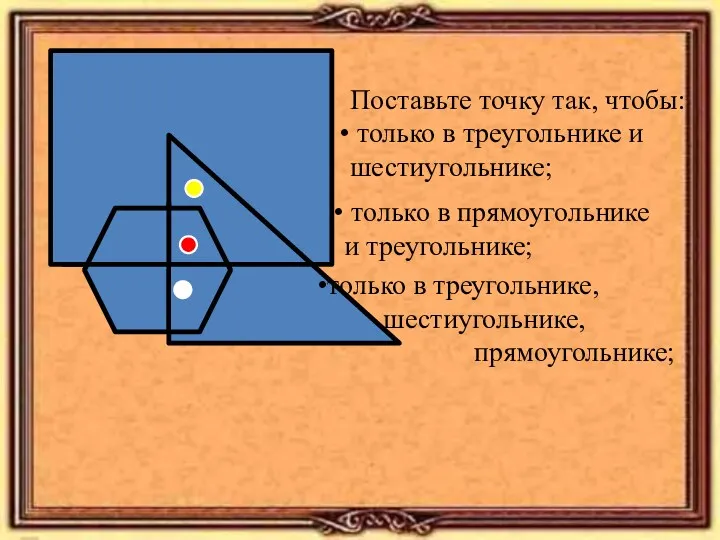 Работа с геометрическими фигурами.
Работа с геометрическими фигурами. Параллелепипед. Тетраэдр. Виды многогранников
Параллелепипед. Тетраэдр. Виды многогранников Средства измерений и их классификация. Лекция 7
Средства измерений и их классификация. Лекция 7 Загадки пирамид
Загадки пирамид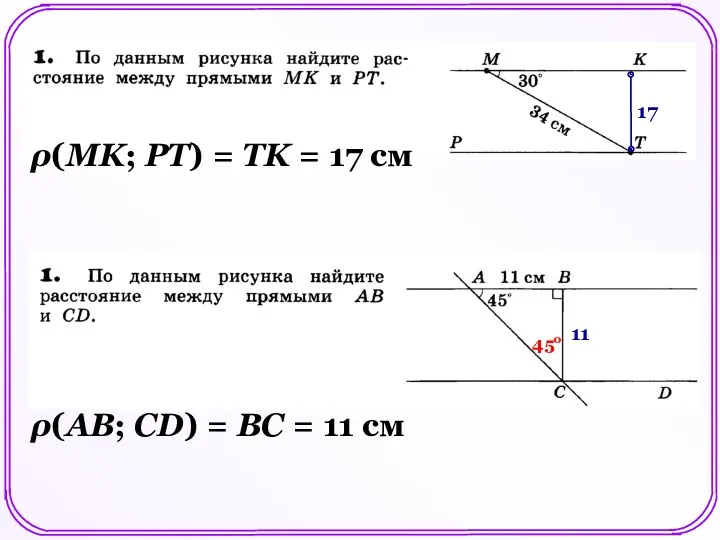 Построение треугольника по трём элементам
Построение треугольника по трём элементам Метрология. Научные изыскания в области метрологии
Метрология. Научные изыскания в области метрологии Полигон и гистограмма. Эмпирическая функция распределения
Полигон и гистограмма. Эмпирическая функция распределения Презентация Состав 6 1 класс УМК Гармония
Презентация Состав 6 1 класс УМК Гармония Статистическое изучение динамики социально-экономических явлений
Статистическое изучение динамики социально-экономических явлений Задачи на движение по реке. Математические модели (9 класс)
Задачи на движение по реке. Математические модели (9 класс) Сложение и вычитание вида 10 + 7, 17 – 7, 17 – 10
Сложение и вычитание вида 10 + 7, 17 – 7, 17 – 10 Единицы массы: тонна и центнер
Единицы массы: тонна и центнер