Содержание
- 2. КОНУС
- 3. Понятие многогранника Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранником. Примеры многогранников
- 4. Виды многогранников Выпуклые Невыпуклые
- 5. Примеры многогранников Большой курносый икосододекаэдр
- 6. Примеры многогранников Большой ромбогексаэдр
- 7. Примеры многогранников Квазиромбокубоктаэдр
- 8. Выпуклый многогранник Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.
- 9. Призма Призмой называется многогранник, который состоит из двух плоских многоугольников, лежащих в разных плоскостях и совмещаемых
- 10. Виды призм Прямая призма Наклонная призма
- 11. Пирамида Многогранник, составленный из n-угольника и n-треугольников называется пирамидой
- 12. Элементы пирамиды 1-высота пирамиды 2-боковая грань пирамиды 3-основание пирамиды
- 13. Гексаэдр Куб составлен из шести квадратов. Каждая его вершина является вершиной трех квадратов. Сумма плоских углов
- 14. Тетраэдр Тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Сумма плоских
- 15. Октаэдр Октаэдр составлен из восьми равносторонних треугольников. Каждая его вершина является вершиной четырех треугольников. Сумма углов
- 16. Додекаэдр Додекаэдр составлен из двенадцати равносторонних пятиугольников. Каждая его вершина является вершиной трех пятиугольников. Сумма плоских
- 17. Икосаэдр Икосаэдр составлен из двадцати равносторонних треугольников. Каждая его вершина является вершиной пяти треугольников. Сумма плоских
- 18. D А С В Поверхность, составленная из четырех треугольников … называется тетраэдром Грани Вершины Ребра Тетраэдр
- 20. D А С В Противоположные ребра основание основание
- 21. А В С D А1 D1 С1 B1 Диагональ параллелепипеда - отрезок, соединяющий противоположные вершины.
- 22. Тетраэдр C A D B Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани
- 23. Параллелепипед Многоугольник, сторонами которого являются отрезки, по которым секущая плоскость пересекает грани параллелепипеда, называется сечением параллелепипеда.
- 24. Сечение тетраэдра Т.к. тетраэдр имеет четыре грани, то его сечениями могут быть только треугольники и четырёхугольники.
- 25. Правила построения сечений ТЕТРАЭДРА а)Проводим прямые через точки, лежащие в одной плоскости; б) Ищем прямые пересечения
- 26. А B D C N M K Как построить сечение тетраэдра DABC плоскостью, проходящей через точки
- 27. А B D C N M K Как построить сечение тетраэдра DABC плоскостью, проходящей через точки
- 28. Построение сечения тетраэдра через точки M, N, K А B D C N M K Построение:
- 29. Построение сечения тетраэдра через точки M, N, K А B D C N M K F
- 30. Построение сечения тетраэдра через точки M, N, K А B D C N M K L
- 31. Построение сечения тетраэдра через точки M, N, K А B D C N M K L
- 32. Секущей плоскостью тетраэдра называют любую плоскость, по обе стороны от которой имеются точки данного тетраэдра.
- 33. Сечение тетраэдра - выпуклый многоугольник, вершинами которого являются точки пересечения секущей плоскости с ребрами тетраэдра, а
- 34. Построить сечение тетраэдра DABC плоскостью, проходящей через данные точки M,K.E. А D B C Е М
- 35. А D B C Е М К ∙ ∙ ∙
- 36. Построить сечение тетраэдра DABC плоскостью, проходящей через точку M, параллельно грани ВСD. А D B C
- 37. Построить сечение тетраэдра DABC плоскостью, проходящей через точку Е параллельно грани АВС. А D B C
- 38. Задание Построить сечение тетраэдра ABCD, проходящее через точку R параллельно грани BCD. Построить сечение тетраэдра ABCD,
- 42. ∙
- 45. А С В D N P Q R На ребрах AB, AD, CD тетраэдра ABCD отмечены
- 46. Построить сечение тетраэдра ABCD, проходящее через три данные точки R, S, T.
- 47. ∙ ∙ R T S ∙ . Q L Построение. RS TS 3. TS∩DC=L 4. LR∩AD=Q
- 48. ∙ ∙ R T S ∙ 5. L F
- 49. ∙ ∙ R T S ∙ 5. . F .L
- 50. L . Q . R
- 51. . L . Q
- 52. . L . Q
- 53. L
- 54. Найди ошибку.
- 55. Найди ошибку.
- 56. Найди ошибку. 10
- 57. Найди ошибку. 10
- 58. Индивидуальное задание Построить сечение тетраэдра по данным точкам
- 59. Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами рёбер. А B С D
- 60. Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся его вершинами. А B С D
- 61. Постройте сечение куба плоскостью, проходящей через три данные точки. А B С D D1 С1 B1
- 62. A B С B1 D1 D K M C1 A1 ВАЖНО! Если секущая плоскость пересекает противоположные
- 63. Постройте сечение куба плоскостью, проходящей через три данные точки. А B С D D1 С1 B1
- 64. Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер. А B С
- 65. Постройте сечение куба плоскостью, проходящей через три данные точки, являющиеся серединами его рёбер. А B С
- 66. Постройте сечение куба, проходящее через точки, выделенные на рисунке. А B С D D1 С1 B1
- 67. Постойте сечение параллелепипеда плоскостью, проходящей через указанные точки. Если секущая плоскость пересекает противоположные грани параллелепипеда по
- 69. Практическая работа. Постройте сечение многогранника плоскостью, проходящей через указанные точки. M A А1 1) 1) 2)
- 70. Проверьте правильность построения сечения. M A А1 1) 2) В С К В A С A
- 71. A B C D K L M N F G Проводим через точки F и O
- 72. A B C D K L M N F G Шаг 2: ищем след секущей плоскости
- 73. A B C D K L M N F G O E Шаг 3: делаем разрезы
- 74. C B A D K L M N F G Шаг 4: выделяем сечение многогранника Все
- 75. Задание № 1 Задание № 2 Построй сечения призмы по трем данным точкам. А теперь проверь
- 77. A D C B C1 B1 A1 D1 M N K A D C B C1
- 78. А В C D
- 79. Решение задач
- 80. Да, путь познания не гладок. Но знайте вы со школьных лет: Загадок больше, чем разгадок. И
- 81. В тетраэдре ABCD на ребре АВ отмечена точка М. Постройте сечение тетраэдра плоскостью, параллельной AC и
- 82. A B C D B1 C1 D1 M N K Выбираем точки М и N, принадлежащие
- 83. A B C D B1 C1 D1 M N K A1 E Теперь обращаем внимание, что
- 84. A B C D B1 C1 D1 M N K A1 E Точки Е и К
- 85. A B C D B1 C1 D1 M N K A1 E F Далее видим, что
- 86. A B C D B1 C1 D1 M N K A1 E F G Полученная точка
- 87. A B C D C1 D1 M N K A1 E F G H Остается соединить
- 88. M N K Построить сечение четырехугольной пирамиды, заданное точками M,N и K. Проследите за ходом построения
- 89. Построить сечение пятиугольной призмы, заданное точками M,N и K. Проследите за ходом построения сечения и запишите
- 90. M N K Рассмотрим теперь более сложные примеры ПРИМЕР 4.
- 91. Постройте сечение пирамиды плоскостью, проходящей через три точки M,N,P. XY – след секущей плоскости на плоскости
- 92. XY – след секущей плоскости на плоскости основания D C B Z Y X M N
- 93. Домашнее задание 1 вариант 2 вариант
- 95. Скачать презентацию
 Приемы умножения и деления на 10
Приемы умножения и деления на 10 Методы прогнозирования
Методы прогнозирования Треугольники. Обучающая программа по геометрии
Треугольники. Обучающая программа по геометрии Анализ эмпирических данных. (Тема 9)
Анализ эмпирических данных. (Тема 9) Свойство медианы равнобедренного треугольника
Свойство медианы равнобедренного треугольника Основы теории графов. Операции над графами
Основы теории графов. Операции над графами Конус. Решение задач
Конус. Решение задач Таблицы истинности
Таблицы истинности Итоговое повторение. Задачи на сравнение. 4 класс
Итоговое повторение. Задачи на сравнение. 4 класс Приём письменного деления на однозначное число
Приём письменного деления на однозначное число Взаимное расположение прямой и плоскости в пространстве
Взаимное расположение прямой и плоскости в пространстве Электронное дидактическое пособие Вставь недостающую фигуру
Электронное дидактическое пособие Вставь недостающую фигуру Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве
Элементы аналитической геометрии на прямой, плоскости и в трехмерном пространстве Отображения и функции
Отображения и функции Свойства последовательности. Функция
Свойства последовательности. Функция Четырехугольники. Свойства четырехугольников. Решение задач
Четырехугольники. Свойства четырехугольников. Решение задач Вивчаємо арифметичні дії множення і ділення; табличне множення і ділення
Вивчаємо арифметичні дії множення і ділення; табличне множення і ділення Геометрические тела
Геометрические тела Мәдениетінде математика ғылымының дамуы
Мәдениетінде математика ғылымының дамуы тест по математике для 2 класса, конец года
тест по математике для 2 класса, конец года Маленькая принцесса
Маленькая принцесса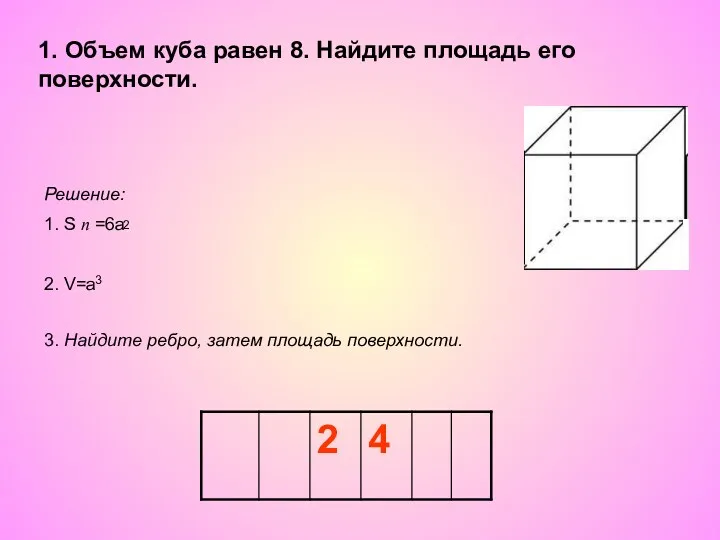 Все объемы. Задачи
Все объемы. Задачи Десятичные дроби
Десятичные дроби Тренажёр по математике (2 класс)
Тренажёр по математике (2 класс) Сложение и вычитание дробей с разными знаменателями
Сложение и вычитание дробей с разными знаменателями Сколько в пуде, соли. Познавательное чтение
Сколько в пуде, соли. Познавательное чтение Тест на уравнения (5 класс)
Тест на уравнения (5 класс) Второй и третий признаки равенства треугольников. 7 класс
Второй и третий признаки равенства треугольников. 7 класс