Содержание
- 2. Цель обучения: 11.2.6 - знать взаимное расположение прямой и плоскости в пространстве. Цель урока: - рассмотреть
- 3. Повторим! Каноническое уравнение прямой Пусть прямая L проходит через данную точку М0(x0; y0; z0) параллельно вектору:
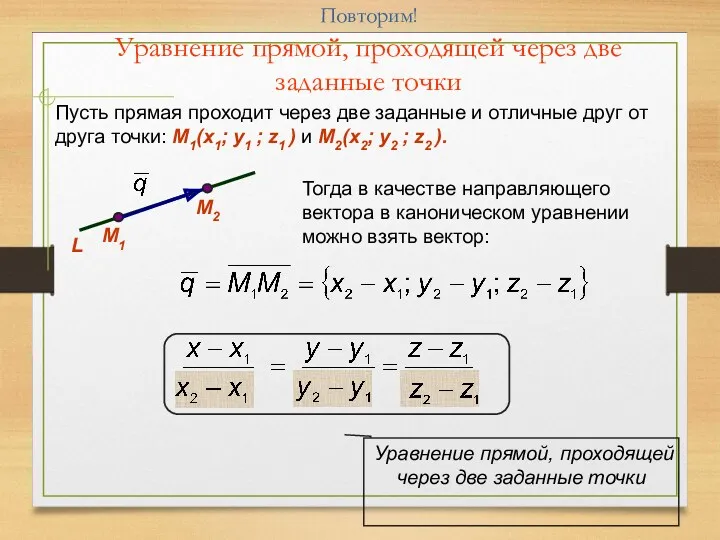
- 4. Повторим! Уравнение прямой, проходящей через две заданные точки Пусть прямая проходит через две заданные и отличные
- 5. Повторим! Параметрическое уравнение прямой При решении многих практических задач используют параметрическое уравнение прямой, которое получается из
- 6. Повторим! Общее уравнение плоскости Если в пространстве фиксирована произвольная декартова система координат Oxyz, то всякое уравнение
- 7. Повторим! Общее уравнение плоскости Произвольная точка М(x; y; z) лежит на плоскости, если ее координаты удовлетворяют
- 8. Взаимное расположение прямой и плоскости в пространстве Пусть в пространстве заданы плоскость λ и прямая ℓ
- 9. а) Если прямая параллельна плоскости или прямая принадлежит плоскости, то (1) или в координатной форме Am
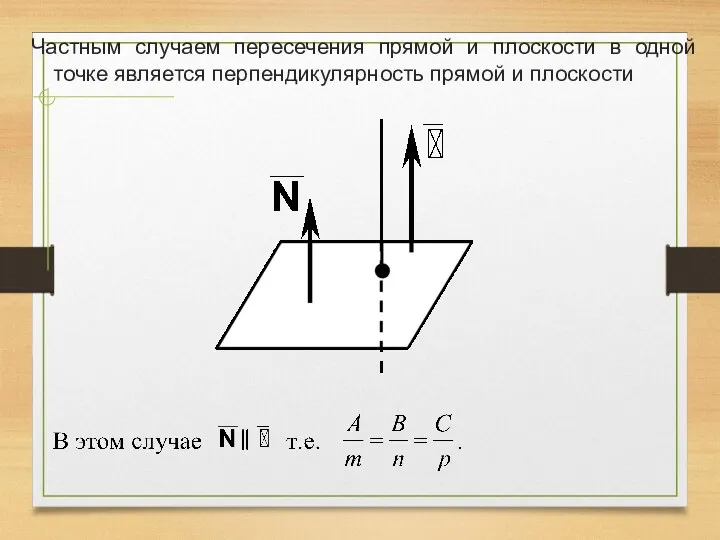
- 10. Частным случаем пересечения прямой и плоскости в одной точке является перпендикулярность прямой и плоскости
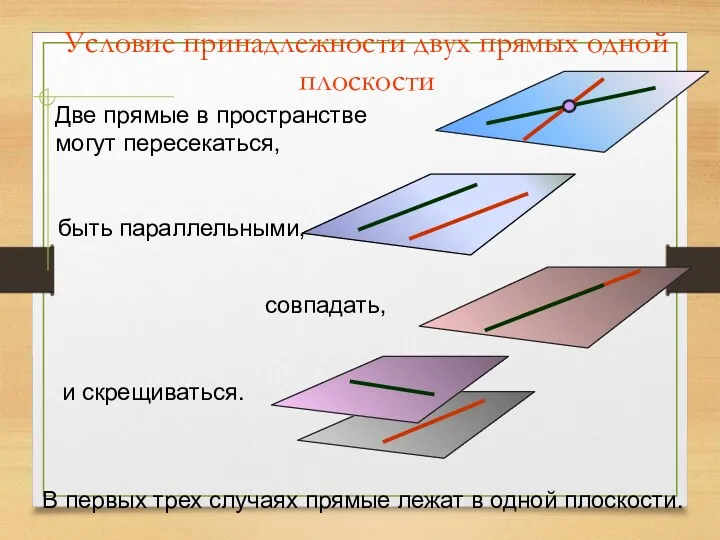
- 11. Условие принадлежности двух прямых одной плоскости Две прямые в пространстве могут пересекаться, быть параллельными, и скрещиваться.
- 12. Условие принадлежности двух прямых одной плоскости Пусть две прямые заданы каноническими уравнениями: Для принадлежности двух прямых
- 13. Точка пересечения прямой и плоскости При вычислении координат точки пересечения прямой и плоскости следует совместно решить
- 14. Точка пересечения прямой и плоскости Подставить t0 в параметрическое уравнение прямой: Подставить в уравнение плоскости вместо
- 15. Пример Найти точку пересечения прямой и плоскости. Напишем параметрическое уравнение прямой: Подставим в уравнение плоскости: Подставим
- 16. Упражнение 1 Определите взаимное расположение прямой, задаваемой уравнениями и плоскости, задаваемой уравнением x – 3y +
- 17. Упражнение 2 Найдите координаты точки пересечения плоскости 2x – y + z – 3 = 0
- 19. Скачать презентацию













 Объем параллелепипеда. Математика. 6 класс
Объем параллелепипеда. Математика. 6 класс Геометричні перетворення на площині. Геометрія. 9 клас
Геометричні перетворення на площині. Геометрія. 9 клас Геометрические тела
Геометрические тела Математический поезд.
Математический поезд. Урок математики 1 класс по теме Сложение и вычитание в пределах 20 без перехода через десяток УМК Перспектива
Урок математики 1 класс по теме Сложение и вычитание в пределах 20 без перехода через десяток УМК Перспектива Разложение на множители. Формулы сокращённого умножения. Алгебра 7 класс
Разложение на множители. Формулы сокращённого умножения. Алгебра 7 класс Математический диктант
Математический диктант Вычисление тройных интегралов
Вычисление тройных интегралов Определение числового ряда. Сходимость. (Лекция 9)
Определение числового ряда. Сходимость. (Лекция 9) Интересные математические факты
Интересные математические факты Своя Игра для учащихся 9 класса
Своя Игра для учащихся 9 класса Турнир знатоков математики. 7-8 класс
Турнир знатоков математики. 7-8 класс Пересечение поверхностей вращения
Пересечение поверхностей вращения Путешествие в страну математики
Путешествие в страну математики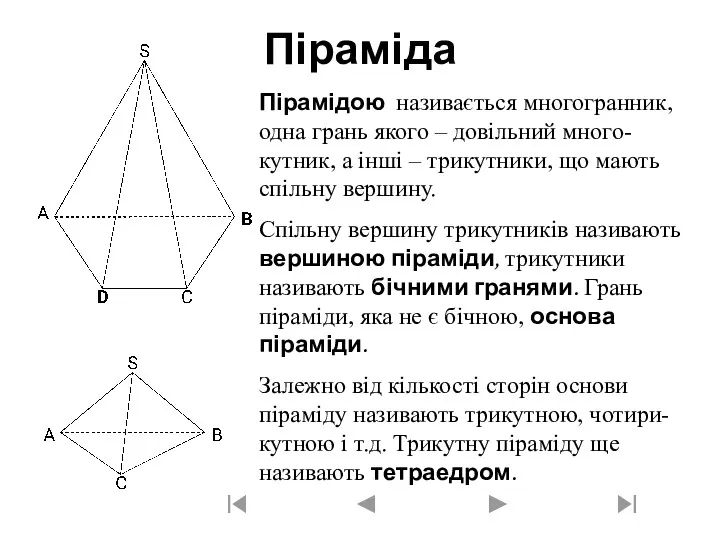 Многогранник піраміда
Многогранник піраміда Задачи на нахождение неизвестного по двум разностям 4 класс(практичекий материал)
Задачи на нахождение неизвестного по двум разностям 4 класс(практичекий материал) Статистика и теория вероятностей. Испытание. Успех и неудача. Серия испытаний до первого успеха. 9 класс
Статистика и теория вероятностей. Испытание. Успех и неудача. Серия испытаний до первого успеха. 9 класс Третий признак равенства треугольников по трем сторонам
Третий признак равенства треугольников по трем сторонам Презентация к уроку математики Состав чисел в пределах 10. Закрепление и повторение
Презентация к уроку математики Состав чисел в пределах 10. Закрепление и повторение Анализ временных рядов. (Тема 5)
Анализ временных рядов. (Тема 5)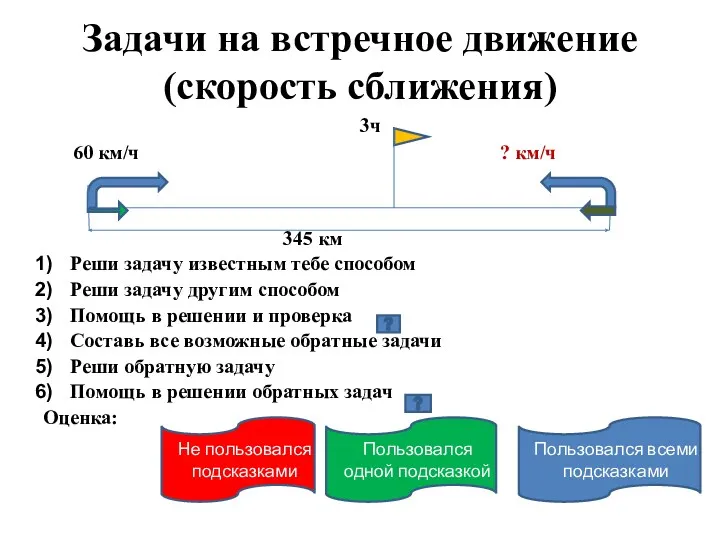 Интерактивный плакат Задачи на встречное движение (скорость сближения) - математика 4 класс
Интерактивный плакат Задачи на встречное движение (скорость сближения) - математика 4 класс Тест. Задания В13, ЕГЭ по математике
Тест. Задания В13, ЕГЭ по математике Презентация к открытому уроку по математике на тему Умножение девяти и на 9,соответствующие случаи деления
Презентация к открытому уроку по математике на тему Умножение девяти и на 9,соответствующие случаи деления Методы оптимальных решений № 1. Задачи линейного программирования и графический метод решения
Методы оптимальных решений № 1. Задачи линейного программирования и графический метод решения Приёмы сложения однозначных чисел с переходом через десяток
Приёмы сложения однозначных чисел с переходом через десяток Устный счет. Сложение с переходом через десяток. Часть 1
Устный счет. Сложение с переходом через десяток. Часть 1 6.9
6.9 Пирамида
Пирамида