Содержание
- 2. Identify polynomial functions. Recognize characteristics of graphs of polynomial functions. Determine end behavior. Use factoring to
- 3. Definition of a Polynomial Function Let n be a nonnegative integer and let be real numbers,
- 4. Graphs of Polynomial Functions – Smooth and Continuous Polynomial functions of degree 2 or higher have
- 5. End Behavior of Polynomial Functions The end behavior of the graph of a function to the
- 6. The Leading Coefficient Test As x increases or decreases without bound, the graph of the polynomial
- 7. The Leading Coefficient Test for (continued)
- 8. Example: Using the Leading Coefficient Test Use the Leading Coefficient Test to determine the end behavior
- 9. Zeros of Polynomial Functions If f is a polynomial function, then the values of x for
- 10. Example: Finding Zeros of a Polynomial Function Find all zeros of We find the zeros of
- 11. Example: Finding Zeros of a Polynomial Function (continued) Find all zeros of The zeros of f
- 12. Multiplicity and x-Intercepts If r is a zero of even multiplicity, then the graph touches the
- 13. Example: Finding Zeros and Their Multiplicities Find the zeros of and give the multiplicities of each
- 14. Example: Finding Zeros and Their Multiplicities (continued) We find the zeros of f by setting f(x)
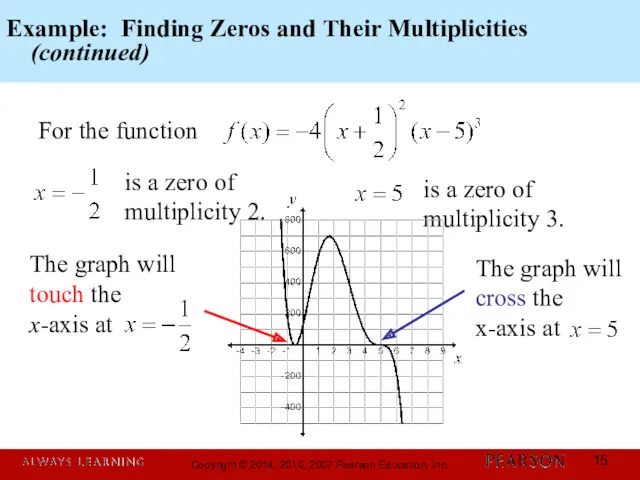
- 15. Example: Finding Zeros and Their Multiplicities (continued) For the function is a zero of multiplicity 2.
- 16. The Intermediate Value Theorem Let f be a polynomial function with real coefficients. If f(a) and
- 17. Example: Using the Intermediate Value Theorem Show that the polynomial function has a real zero between
- 18. Example: Using the Intermediate Value Theorem (continued) For f(–3) = –42 and f(–2) = 5. The
- 19. Turning Points of Polynomial Functions In general, if f is a polynomial function of degree n,
- 20. A Strategy for Graphing Polynomial Functions
- 21. Example: Graphing a Polynomial Function Use the five-step strategy to graph Step 1 Determine end behavior
- 22. Example: Graphing a Polynomial Function (continued) Use the five-step strategy to graph Step 2 Find x-intercepts
- 23. Example: Graphing a Polynomial Function (continued) Use the five-step strategy to graph Step 2 (continued) Find
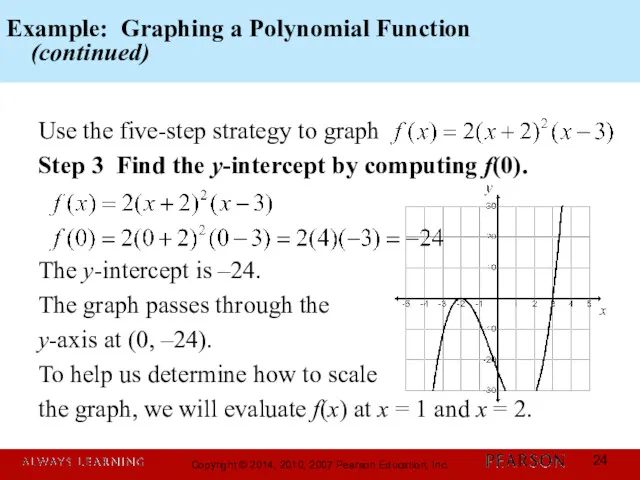
- 24. Example: Graphing a Polynomial Function (continued) Use the five-step strategy to graph Step 3 Find the
- 25. Example: Graphing a Polynomial Function (continued) Use the five-step strategy to graph Step 3 (continued) Find
- 26. Example: Graphing a Polynomial Function (continued) Use the five-step strategy to graph Step 4 Use possible
- 27. Example: Graphing a Polynomial Function (continued) Use the five-step strategy to graph Step 4 (continued) Use
- 29. Скачать презентацию
























 Представление рациональных чисел в виде десятичной дроби (продолжение)
Представление рациональных чисел в виде десятичной дроби (продолжение) Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20
Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20 Умножение натуральных чисел и его свойства. 5 класс
Умножение натуральных чисел и его свойства. 5 класс Арифметическая игра Числовые Домики
Арифметическая игра Числовые Домики Умножение и деление обыкновенных дробей
Умножение и деление обыкновенных дробей Смешанные числа. Обыкновенные дроби. Математика. 5 класс
Смешанные числа. Обыкновенные дроби. Математика. 5 класс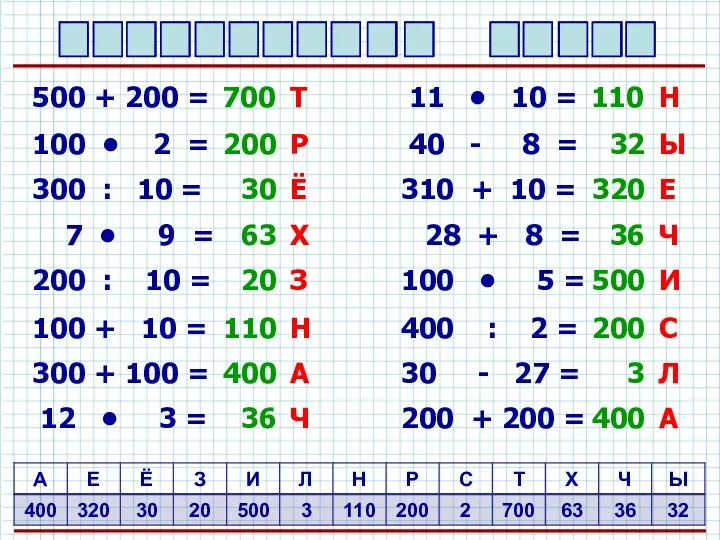 Сложение и вычитание трёхзначных чисел Презентация к уроку математики 3 класс
Сложение и вычитание трёхзначных чисел Презентация к уроку математики 3 класс Деление (математика, 3 класс, УМК Гармония)
Деление (математика, 3 класс, УМК Гармония) Презентация Времена года
Презентация Времена года ЦМР к уроку математики в 1 классе Дециметр - новая единица длины
ЦМР к уроку математики в 1 классе Дециметр - новая единица длины Признаки делимости на 10, на 5 и на 2
Признаки делимости на 10, на 5 и на 2 Множества и матрицы
Множества и матрицы Презентация Веселая математика с Винни-Пухом
Презентация Веселая математика с Винни-Пухом Площадь треугольника
Площадь треугольника Двузначные числа
Двузначные числа Решение задач с помощью кругов Эйлера
Решение задач с помощью кругов Эйлера Десятичные дроби и действия над ними
Десятичные дроби и действия над ними Окружность. Касательная к окружности
Окружность. Касательная к окружности Распределительное свойство умножения
Распределительное свойство умножения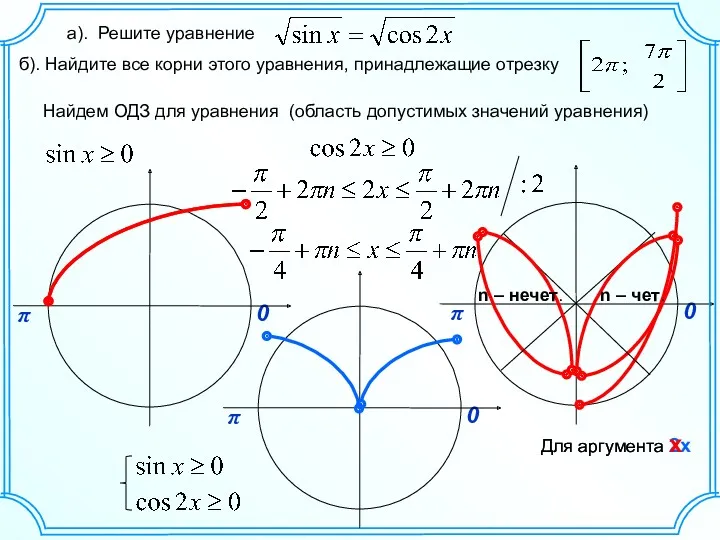 Решение тригонометрического уравнения (С 1, 26)
Решение тригонометрического уравнения (С 1, 26) Методические разработки учителя математики
Методические разработки учителя математики Скорость. Время. Расстояние
Скорость. Время. Расстояние Презентация к уроку математики в 4 классе.
Презентация к уроку математики в 4 классе. презентация к уроку математики Решение задач на движение
презентация к уроку математики Решение задач на движение Дисперсия дискретной случайной величины
Дисперсия дискретной случайной величины Экономические задачи в заданиях ЕГЭ по математике
Экономические задачи в заданиях ЕГЭ по математике Приёмы устных вычислений вида 450+30; 620-200
Приёмы устных вычислений вида 450+30; 620-200 Сложение и вычитание десятичных дробей. Урок 111
Сложение и вычитание десятичных дробей. Урок 111