Слайд 2

Решение. Полагая y = const, находим
Слайд 3

Полагая x = const, находим
Слайд 4

Пример. Найти значения частных производных функции
в точке M(1, –1, 0).
Слайд 5

Решение. Полагая y = const, z = const, находим
Слайд 6
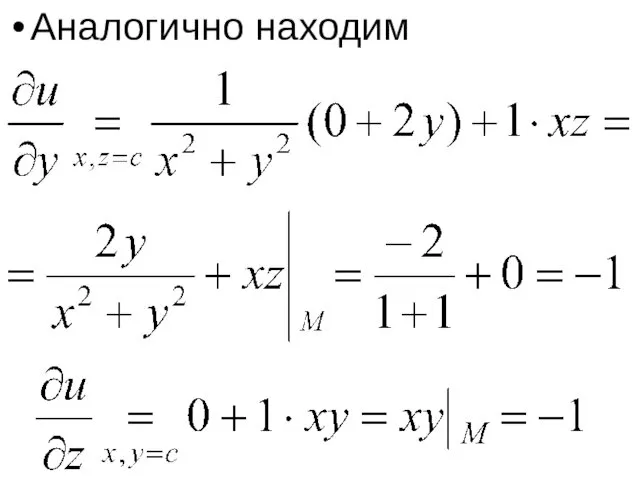
Слайд 7

Геометрическим смыслом частной производной (например, ) является тангенс угла наклона касательной,
проведенной в точке M0(x0, y0, z0) к сечению поверхности плоскостью у = у0.
Слайд 8

Предположим, что функция z = f(x, y) имеет непрерывные частные производные
Слайд 9

Эти производные в свою очередь являются функциями независимых переменных x и
y. Будем называть
и частными производными 1-го порядка.
Слайд 10

Частными производными 2-го порядка называются частные производные от частных производных 1-го
порядка.
Для функции z = f(x, y) двух переменных можно найти четыре частные производные 2-го порядка, которые обозна-чаются следующим обр-м:
Слайд 11

Слайд 12

В общем случае смешанные частные производные могут не совпадать, однако для
них справедлива теорема:
Теорема. Если смешанные частные производные и непрерывны в некоторой точке M(x, y), то они равны, т. е.
Слайд 13

Частными производными n–го порядка называются частные производные от частных производных (n – 1)–го
порядка.
Их обозначают
и т. д.
Слайд 14

Частные производные любого порядка, взятые по различным переменным, называются смешанными.
Слайд 15

Пример. Найти частные производные 2-го порядка функции
Слайд 16

Решение. Последовательно находим
Слайд 17
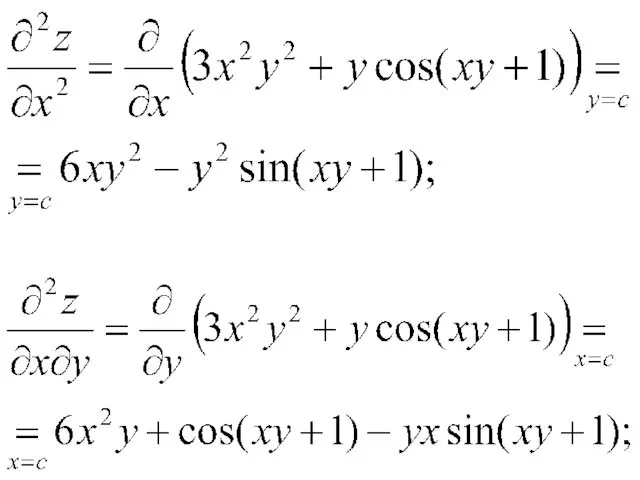
Слайд 18
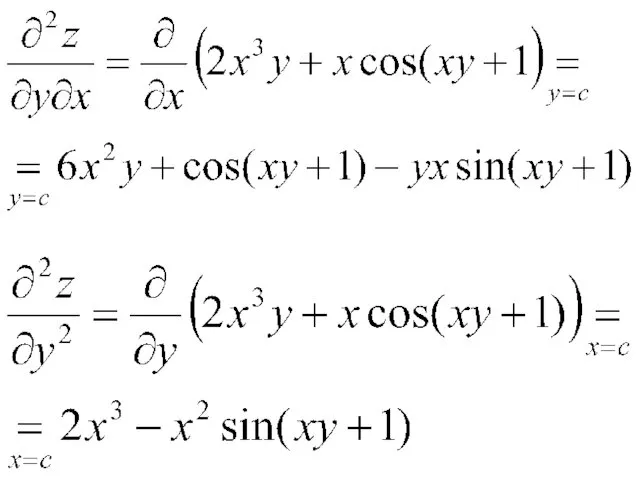
Слайд 19

§ 5. Дифференциал функции нескольких переменных
Слайд 20

Рассмотрим функцию z = f(x, y). Дадим аргументу x приращение Δx, а аргументу y
приращение Δy. Тогда z получит приращение
которое называется полным приращением функции z.
Слайд 21

Предположим, что f(x, y) в точке M(x, y) имеет непрерывные частные производные.
Слайд 22

Определение. Дифференциалом 1-го порядка функции z = f(x, y) называется главная часть полного приращения
Δz этой функции, линейная относительно Δx и Δy, обозначается символом dz или df и вычисляется по формуле
Слайд 23

Так как дифференциалы независимых переменных совпадают с их приращениями, т.е. dx = Δx,
dy = Δy, то эту формулу можно записать в виде:
Слайд 24

Геометрическим смыслом полного дифференциала функции двух переменных f(x, y) в точке
(х0, у0) является приращение аппликаты (координаты z) касательной плоскости к поверхности при переходе от точки (х0, у0) к точке (х0+Δх, у0+Δу).
Слайд 25

Геометрический смысл полного дифференциала функции двух переменных является пространственным аналогом геометрического
смысла дифференциала функции одной переменной.
Слайд 26

Дифференциалом 2-го порядка функции z = f(x, y) называется дифференциал от ее дифференциала 1-го
порядка и обозначается
Слайд 27

Если все частные производные 2-го порядка функции z = f(x, y) непрерывны, то имеет
место формула:
Слайд 28

Аналогично определяется дифференциал n–го порядка:
Слайд 29

Пример. Найти дифференциалы 1-го и 2-го порядков функции
Слайд 30

Решение. Найдем частные производные 1-го и 2-го порядков:
Слайд 31
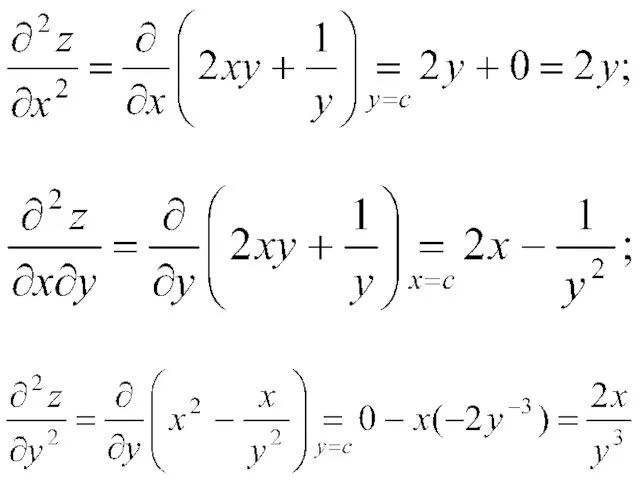
Слайд 32

Следовательно, дифференциалы 1-го и 2-го порядков запишутся в виде:
Слайд 33

Приближенные вычисления с помощью полного дифференциала
Слайд 34

Пусть функция f(x, y) дифференцируема в точке (х, у). Найдем полное
приращение этой функции:
Слайд 35

Если подставить в эту формулу выражение
то получим приближенную формулу:
Слайд 36

Пример. Вычислить приближенно значение
исходя из значения функции
при x =
1, y = 2, z = 1
Слайд 37

Решение. Из заданного выражения определим
Δx = 1,04 – 1
= 0,04,
Δy = 1,99 – 2 = -0,01,
Δz = 1,02 – 1 = 0,02.
Найдем значение функции u(x, y, z) =
Слайд 38
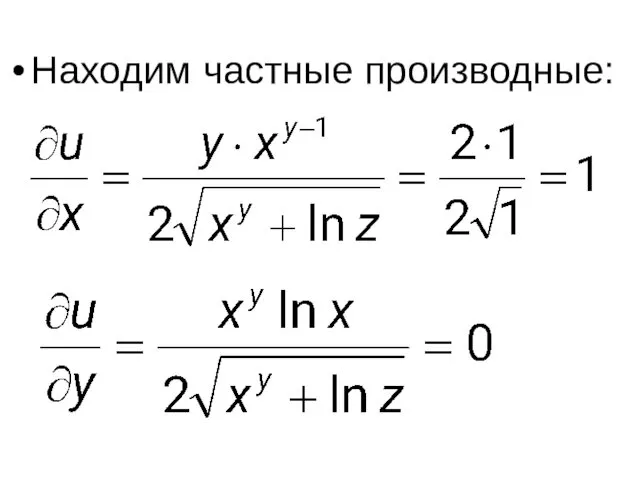
Находим частные производные:
Слайд 39

Полный дифференциал функции u равен:
Слайд 40
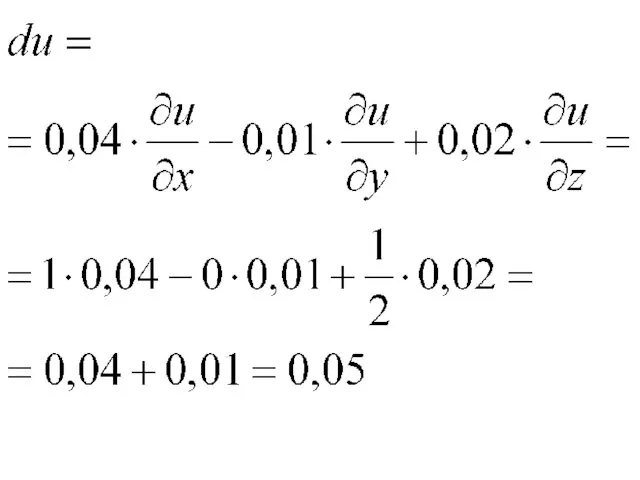
Слайд 41

Точное значение этого выражения: 1,049275225687319176.
Слайд 42

§ 6. Касательная плоскость и нормаль к поверхности
Слайд 43

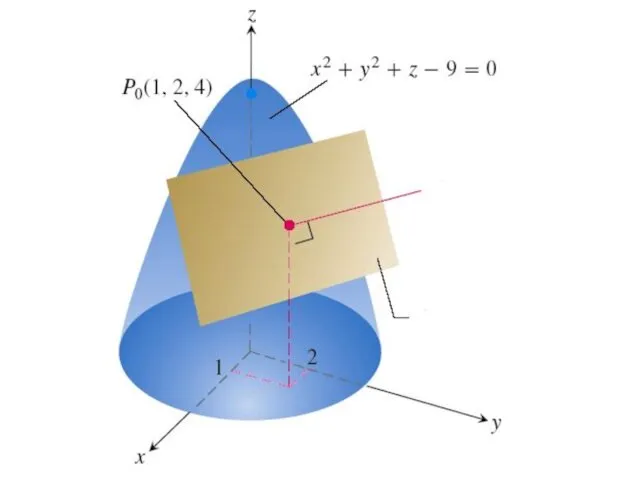
Касательной плоскостью к поверхности в ее точке M0 называется плоскость, которая
содержит все касательные к кривым, проведенным на поверхности через эту точку.
Слайд 44

Нормалью к поверхности в точке M0 называется прямая, проходящая через эту
точку и перпендикулярная касательной плоскости, проведенной в данной точке.
Слайд 45
Слайд 46

Если поверхность задана уравнением F(x, y, z) = 0 то уравнение касательной плоскости в точке
M0(x0, y0, z0) имеет вид:
Слайд 47

Уравнения нормали, проведенной к поверхности в точке M0(x0, y0, z0), запишутся следующим образом:
Слайд 48

Если поверхность задана уравнением z = f(x, y), то уравнение касательной плоскости в точке
M0(x0, y0, z0) имеет вид:
Слайд 49

а уравнения нормали запишутся так:
Слайд 50

Пример. Составить уравнения касательной плоскости и нормали к поверхности
в точке
M0(x0, y0, z0), если
Слайд 51

Решение. Подставляя x0 и y0 в уравнение поверхности, находим значение z0:
откуда
находим z0 = 1. Следовательно, M0(2, –1, 1) – точка касания.
Слайд 52

По условию задачи поверхность задана неявно. Обозначим
и найдем частные производные
в точке M0(2, –1, 1):
Слайд 53
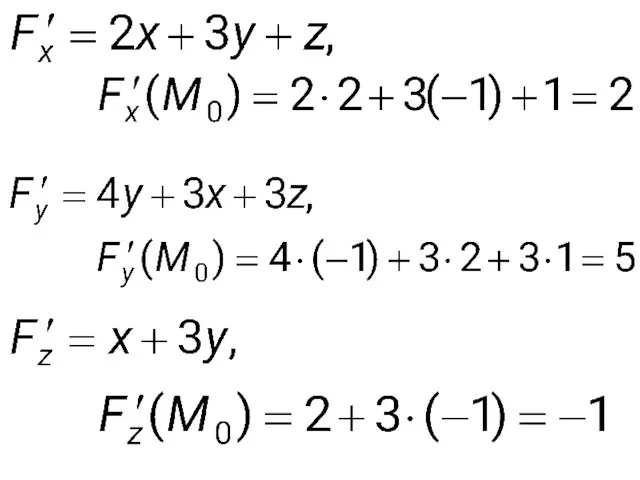
Слайд 54

Подставляем найденные значения частных производных в уравнение касательной плоскости
Слайд 55

и получаем искомое уравнение касательной плоскости:
Слайд 56
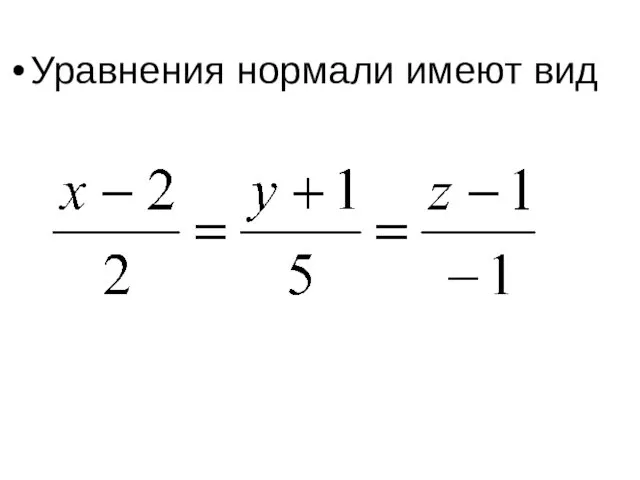
Уравнения нормали имеют вид
Слайд 57

§ 7. Экстремум функции двух переменных
Слайд 58

Определение. Функция z = f(x, y) имеет максимум в точке M0(x0, y0), если существует такая
окрестность этой точки, что для любых точек M(x, y) из этой окрестности выполняется неравенство
Слайд 59
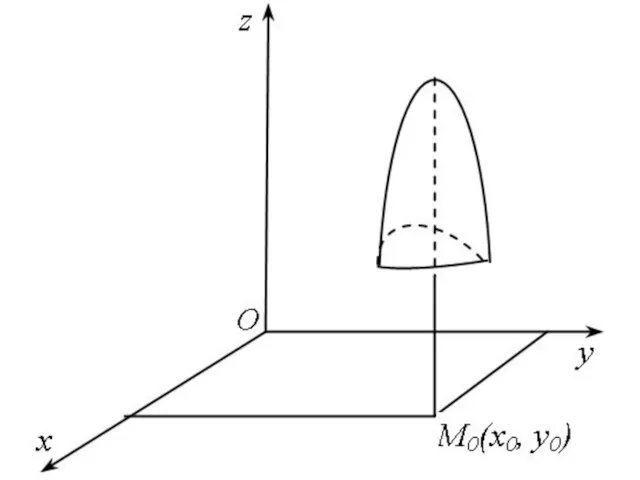
Слайд 60

Определение. Функция z = f(x, y) имеет минимум в точке M0(x0, y0), если существует такая
окрестность этой точки, что для любых точек M(x, y) из этой окрестности выполняется неравенство
Слайд 61
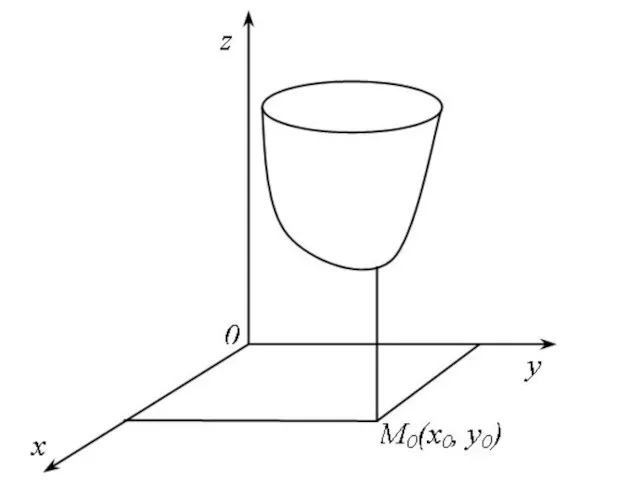
Слайд 62

Точки максимума и минимума называют точками экстремума, а значения функции в
этих точках называются экстремальными.
Слайд 63
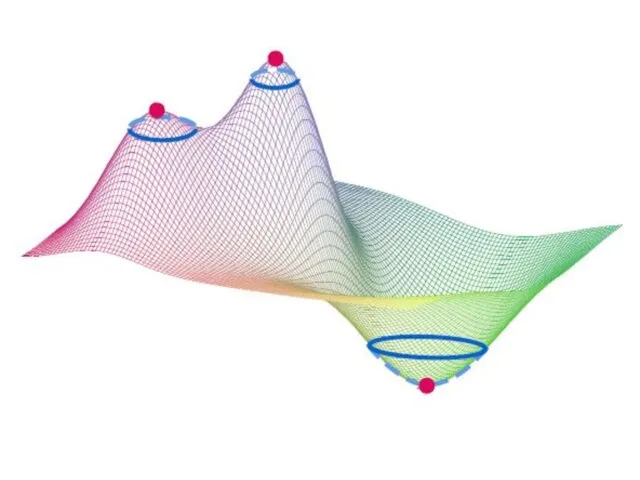
Слайд 64

Теорема 1 (необходимые условия экстремума). Если дифференцируемая функция z = f(x, y) имеет экстремум
в точке M0(x0, y0), то ее частные производные в этой точке равны нулю, т. е.
Слайд 65

Функция z = f(x, y) может иметь экстремум и в точках, где функция непрерывна,
но частные производные не существуют.
Точки, в которых и ,
называются стационарными точками функции z = f(x, y).
Слайд 66

Теорема 2 (достаточные условия экстремума). Пусть M0(x0, y0) является стационарной точкой функции
z = f(x, y) и в ее окрестности существуют непрерывные частные производные 2-го порядка.
Слайд 67

Обозначим
и составим определитель
Тогда:
Слайд 68

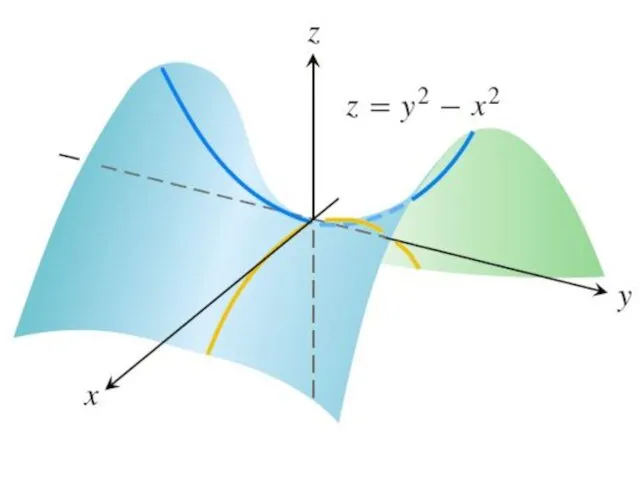
1) если Δ < 0, то в точке M0 нет экстремума;
2) если Δ > 0,
то в точке M0 есть экстремум, причем максимум при A < 0
и минимум при A > 0;
3) если Δ = 0, то требуется дополнительное исследование.
Слайд 69
Слайд 70
Слайд 71
Слайд 72

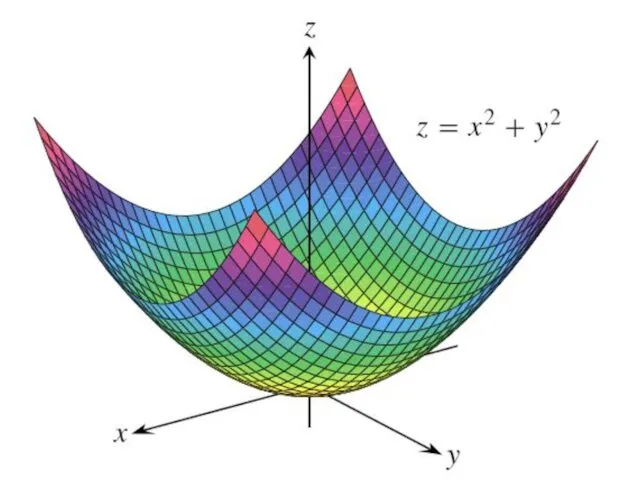
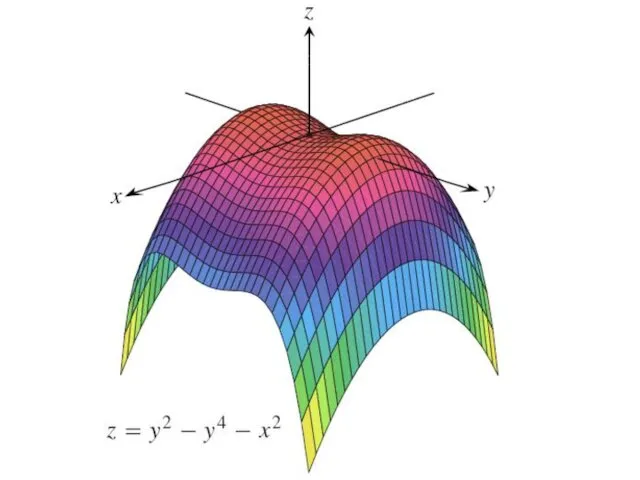
Пример. Исследовать на экстремум функцию
Слайд 73

Решение. Находим частные производные 1-го порядка
Слайд 74

Стационарные точки найдем из системы уравнений
Слайд 75

Получили две стационарные точки: M1(0, 0), и M2(1, 1).
Слайд 76

Находим частные производные 2-го порядка:
Исследуем каждую стационарную точку.
Слайд 77

В точке M1(0, 0) имеем:
A = 0, B = –3, C = 0.
Тогда
Так как
Δ < 0, то в этой точке нет экстремума.
Слайд 78

В точке M2(1, 1) имеем:
A = 6, B = –3, C = 6.
В этом случае
Так как Δ > 0 и A > 0, то в этой точке функция имеет минимум




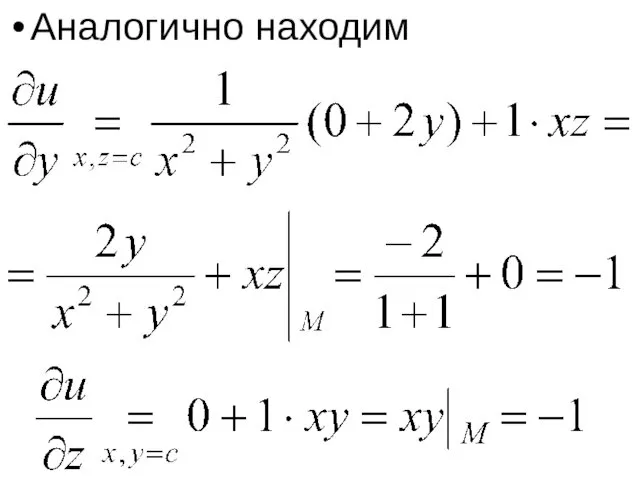










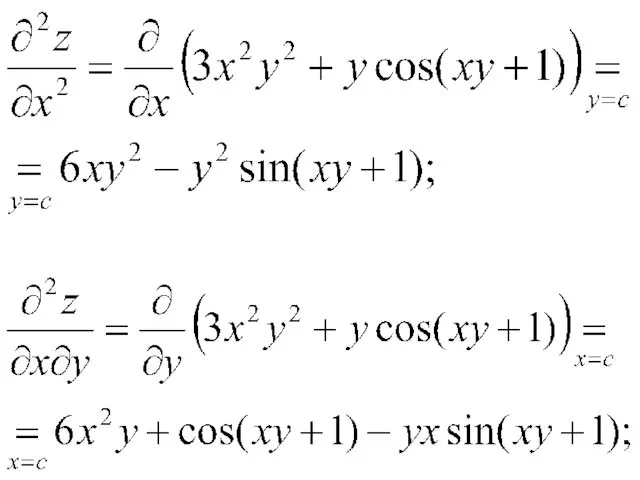
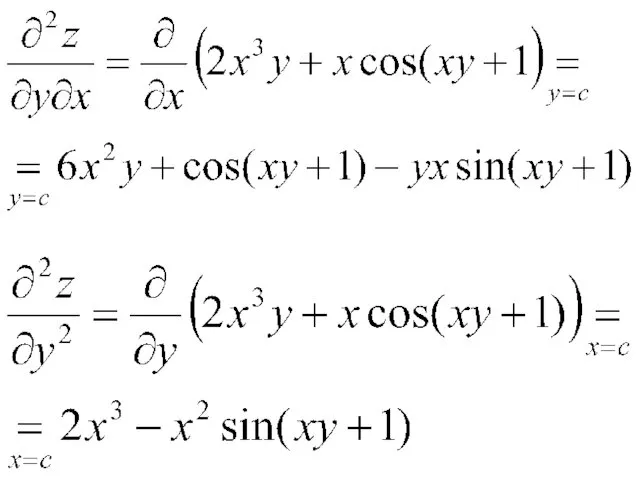












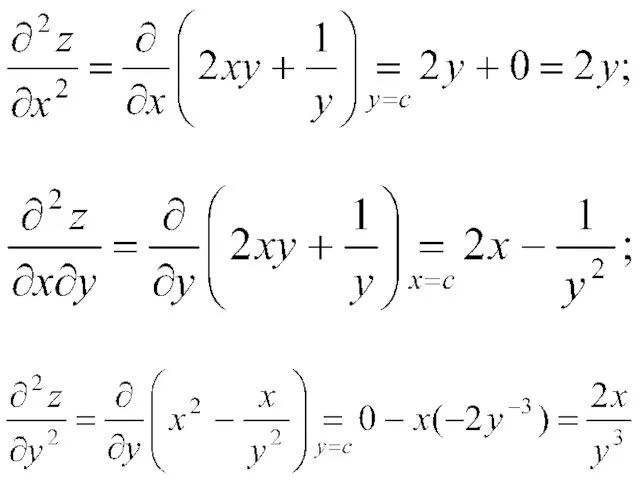






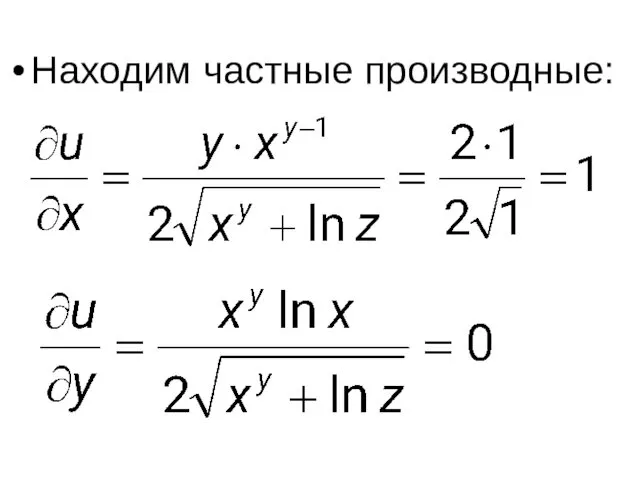

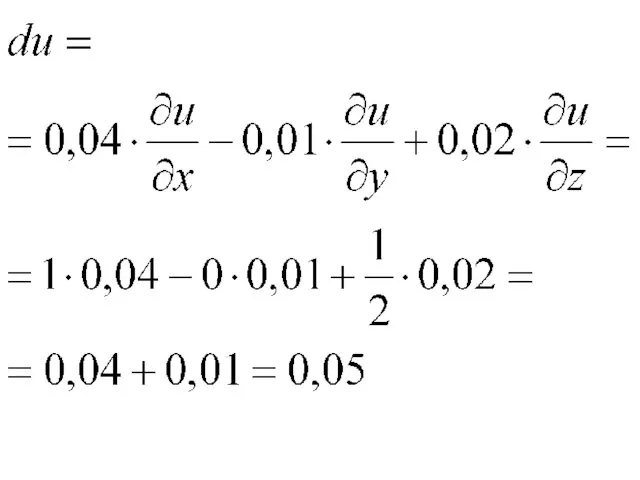












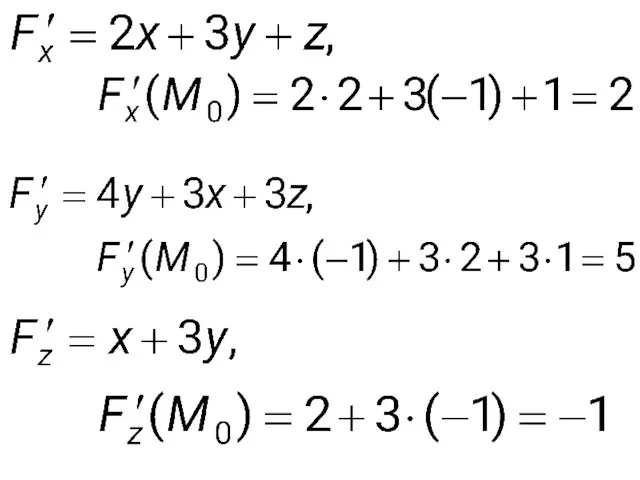


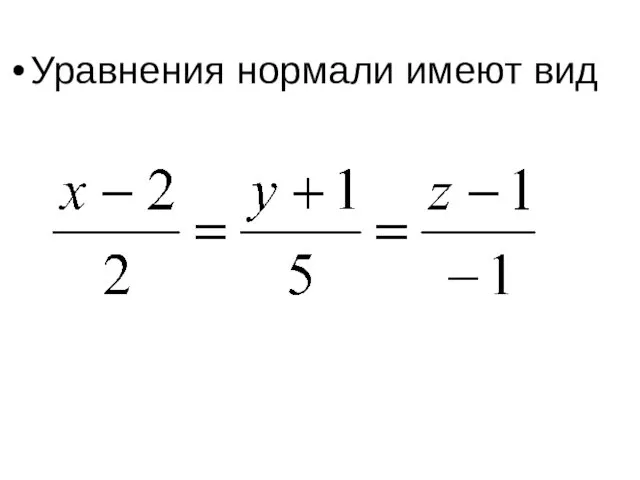






















 Геометрия. 7 класс. Измерение отрезков и углов
Геометрия. 7 класс. Измерение отрезков и углов Признаки равенства прямоугольных треугольников
Признаки равенства прямоугольных треугольников Решение задач. (6 класс)
Решение задач. (6 класс) Кеңістік фигураларын жазықтықта бейнелеу. Параллель проекциялау. Ортогональ проекциялау
Кеңістік фигураларын жазықтықта бейнелеу. Параллель проекциялау. Ортогональ проекциялау Многочлен. Вычисление значений многочлена
Многочлен. Вычисление значений многочлена Урок математики в 4 классе по теме Письменные способы умножения многозначных чисел
Урок математики в 4 классе по теме Письменные способы умножения многозначных чисел Методические рекомендации по формированию навыка работы с таблицей (математика 6 класс)
Методические рекомендации по формированию навыка работы с таблицей (математика 6 класс) Узоры и орнаменты на посуде
Узоры и орнаменты на посуде Устный счет
Устный счет Математические модели. Текстовые задачи по математике
Математические модели. Текстовые задачи по математике Закономерности случайной вариации. Закон нормального распределения. Закон Гауса-Лапласа. (Лекция 3)
Закономерности случайной вариации. Закон нормального распределения. Закон Гауса-Лапласа. (Лекция 3) Устный счёт. Решение выражений
Устный счёт. Решение выражений Самостоятельная математическая деятельность детей дошкольного возраста
Самостоятельная математическая деятельность детей дошкольного возраста Показательная функция
Показательная функция Урок повторения курса геометрии 7-9
Урок повторения курса геометрии 7-9 Задачи (устно)
Задачи (устно) Теория вероятностей. Способность предвидеть возможные варианты будущего
Теория вероятностей. Способность предвидеть возможные варианты будущего Раскрытие скобок
Раскрытие скобок Деление и умножение десятичной дроби (6 класс)
Деление и умножение десятичной дроби (6 класс) Задачи на движение. Скорость
Задачи на движение. Скорость Показательная функция
Показательная функция Интегрированный урок математики с историей
Интегрированный урок математики с историей Внешнее сопряжение двух окружностей
Внешнее сопряжение двух окружностей Ординаты для разбивки переводной кривой стрелочного перевода
Ординаты для разбивки переводной кривой стрелочного перевода 2 Презентация Колличественный счет
2 Презентация Колличественный счет Параллельные прямые. 7 класс
Параллельные прямые. 7 класс Сравнение десятичных дробей
Сравнение десятичных дробей Развитие познавательных способностей.
Развитие познавательных способностей.