Содержание
- 2. Теорема №1 Каждая точка биссектрисы неразвернутого угла равноудалена от его сторон1. Обратно: каждая точка, лежащая внутри
- 3. Доказательство ΔАМК = ΔАМL (т. к. АМ -общая гипотенуза, МК = МL) ⇒ ∠ВАМ = ∠МАС
- 4. Следствие Биссектрисы треугольника пересекаются в одной точке О - точка пересечения биссектрис АА1, ВВ1 ΔАВС. А
- 5. Серединным перпендикуляром к отрезку называется прямая, проходящая через середину данного отрезка и перпендикулярная к нему. А
- 6. Теорема №2 Каждая точка серединного перпендикуляра к отрезку равноудалена от концов этого отрезка. Обратно: каждая точка,
- 7. Доказательство 1) Прямая m- серединный перпендикуляр к отрезку АВ. М А В О m N A
- 8. Следствие Серединные перпендикуляры к сторонам треугольника пересекаются в одной точке. Доказательство: m ⊥ ВА, n ⊥
- 9. Теорема №3 Высоты треугольника (или их продолжения) пересекаются в одной точке. Доказательство Проведем через каждую вершину
- 10. Задача №1 В треугольнике АВС, изображённом на рисунке, АС = ВС = АВ, ВМ = МС.
- 12. Скачать презентацию









 Параллельный перенос
Параллельный перенос Особые приемы при решении логарифмических неравенств
Особые приемы при решении логарифмических неравенств Построение диаграмм и графиков функций
Построение диаграмм и графиков функций 1 сыйныфта телдән исәпләүгә 1-10 эчендә нумерациятемасына презентация.
1 сыйныфта телдән исәпләүгә 1-10 эчендә нумерациятемасына презентация. Обработка результатов измерений
Обработка результатов измерений Цилиндр. Определение, элементы, свойства и многое другое
Цилиндр. Определение, элементы, свойства и многое другое Застосування інтеграла у житті людини
Застосування інтеграла у житті людини презентация к уроку математики в 1 классе по теме Закрепление по теме: Числа от 1 до 20
презентация к уроку математики в 1 классе по теме Закрепление по теме: Числа от 1 до 20 Математика в системі інших наук
Математика в системі інших наук Умножение десятичных дробей на натуральные числа
Умножение десятичных дробей на натуральные числа Процент төшенчәсе белән танышу. Процентлар табу
Процент төшенчәсе белән танышу. Процентлар табу Возникновение и развитие геометрии
Возникновение и развитие геометрии Плотность вероятности
Плотность вероятности Таблица умножения. Тренажер
Таблица умножения. Тренажер Упрощение выражений
Упрощение выражений Геометрія. Самостійна робота
Геометрія. Самостійна робота Градусная мера дуги окружности. 8 класс
Градусная мера дуги окружности. 8 класс Дидактическая игра Чего не стало? Диск
Дидактическая игра Чего не стало? Диск Неопределенный интеграл и его свойства
Неопределенный интеграл и его свойства Числа Фибоначчи
Числа Фибоначчи Название компонентов и результата действия деления
Название компонентов и результата действия деления Правильные многогранники
Правильные многогранники Координатная плоскость
Координатная плоскость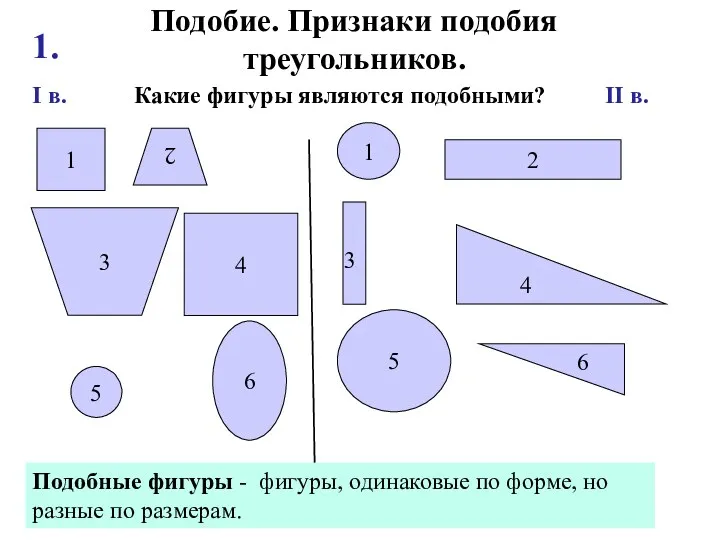 Подобие. Признаки подобия треугольников
Подобие. Признаки подобия треугольников Нахождение неизвестного слагаемого в усложненном уравнении
Нахождение неизвестного слагаемого в усложненном уравнении Обыкновенные дроби. Применение игровой технологии
Обыкновенные дроби. Применение игровой технологии Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов
Векторы в пространстве. Определение вектора в пространстве и связанные с ним понятия, равенство векторов Қызықты математика
Қызықты математика