Численное решение нелинейных уравнений презентация

Постановка задачи
Одной из важных практических задач при исследовании различных свойств математической модели в виде функциональной зависимости y = f(x) является нахождение значений x, при которых эта функция обращается в ноль, т.е. решение уравнения
f(x) = 0. (1)
В общем случае это уравнение носит нелинейный характер.

Этапы численного решения
1) Исследование характера функции f(x), определение количества корней и приблизительного значения интересующего нас корня:
Определяют, какие корни требуется найти, например, только действительные или только положительные корни, наименьший корень и т.д. Популярным методом является графический, который позволяет определить приближенное значение корня или найти отрезок, содержащий один корень функции f(x), т.е. отделить корень.

Если непрерывная функция f(x) на концах отрезка [a, b] принимает значения разных знаков, т.е. если f(a)⋅f(b) < 0, то внутри этого отрезка существует, по крайней мере, один корень уравнения f(x) = 0. Корень будет единственным, если производная f'(x) сохраняет знак внутри интервала (а, b).

2) Вычисление корня с требуемой точностью с помощью какого-либо численного алгоритма.
Уточнение решения, исходя из выбранного начального приближении к истинному корню x*. Для этого используются итерационные методы, позволяющие с помощью рекуррентного соотношения
построить последовательность приближенных решений (xn), сходящуюся к x*. Т. о. стоит задача обеспечения сходимости последовательности к истинному значению корня x*.

Сходимость достигается посредством выбора различными способами функций ϕ, которая зависит от f(x) и в общем случае от номера члена последовательности (n).
Если при нахождении значения xk ≈ x*, используется одно предыдущее значение
(xk-1), то такой метод называется одношаговым.
Если используется m предыдущих значений, то метод называется m-шаговым и, как правило, с увеличением m вычислительные алгоритмы усложняются.

Расчет по рекуррентной последовательности продолжается до тех пор, пока |xn–xn-1| < ε (требуемая точность). Тогда последнее xn выбирается в качестве приближенного значения корня (x* ≈ xn).
На практике имеется большой выбор законов ϕ, что обеспечивает многообразие численных итерационных методов решения нелинейных уравнений.

Метод дихотомии (деления пополам)
А) Отрезок [a, b], на котором находится корень (т.е. выполняется условие f(a)⋅f(b) < 0), последовательно делится на две равные части и определяются знаки функции в точках деления.

Б) При каждом делении проверяется: если в точках деления хi, хi+1 выполнено условие f(хi)⋅f(хi+1) < 0, то на интервале (хi, хi+1) имеется корень уравнения f(x) = 0. Этот интервал затем делится пополам и т.д.
В) Последовательность середин интервалов сходится к искомому решению; процесс останавливается, когда длина интервала станет меньше некоторого заранее заданного значения (точности).

Метод простых итераций
Применяется к уравнению, разрешенному относительно x:
x = ϕ(x).
Переход к этой записи можно сделать многими способами, например, положив ϕ(x)=x+ψ(x) f(x), где ψ(x) ≠ 0 – произвольная непрерывная знакопостоянная функция.
Метод состоит в построении последовательности в виде:
n = 0,1,2,….

Если ϕ(xn) – непрерывная функция, а xn – сходящаяся последовательность, то значение предела этой последовательности и будет искомым решением x*.
Итерационный процесс уточнения корня заканчивается, когда
|xn – xn–1| < ε.
Метод простой итерации является примером одношагового метода и для начала вычислений достаточно знать одно начальное приближение.

Сходимость метода. Отличие (n+1)-го члена последовательности от точного решения можно связать с аналогичной разностью для n-го члена последовательности:
где – некоторая точка между xn и x*. Очевидно, что отрезки должны убывать, а значит всюду должно выполняться соотношение:
| ϕ'(x) | ≤ q < 1.
При этом скорость сходимости увеличивается при уменьшении величины q. Максимальный интервал (α,β), на котором выполняется это условие, называется областью сходимости.

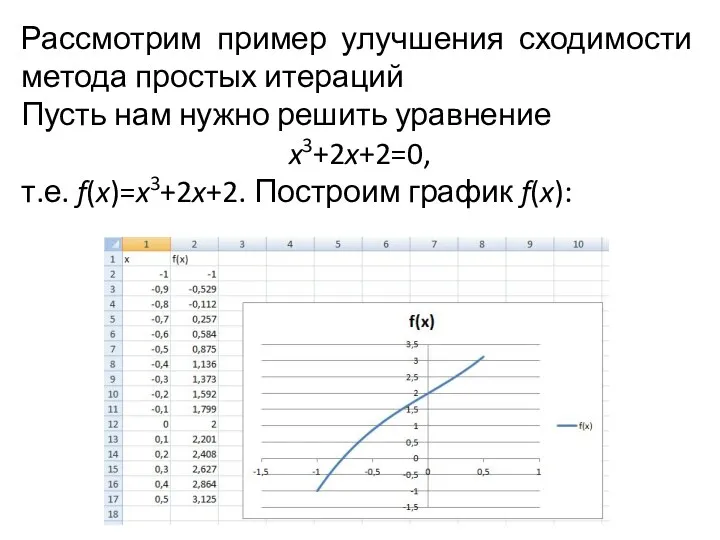
Рассмотрим пример улучшения сходимости метода простых итераций
Пусть нам нужно решить уравнение
x3+2x+2=0,
т.е. f(x)=x3+2x+2. Построим график f(x):

Видно, что решение находится где-то на интервале -1
Чтобы искать решение методом простых итераций, записываем уравнение в виде
x=φ(x), где φ(x)=x+ψ(x)f(x)
Простейший вариант: ψ(x)=1. Но тогда φ’(x)=1+f’(x)=3(1+x2)>1 при -1
Возьмем ψ(x)=a=const. Тогда φ’(x)=1+a(2+3x2). Из условия сходимости |φ’(x)|<1 следует:
-1<1+a(2+3x2)<1 или -2/(2+3x2)
т.е. -1

Метод Ньютона (касательных)
Если функция f(x) непрерывна и дифференцируема, то выбирая ,
получим эквивалентное уравнение
x = x – f(x)/f '(x) =ϕ(x), f '(x) ≠ 0.
Тогда получим следующий итерационный процесс:

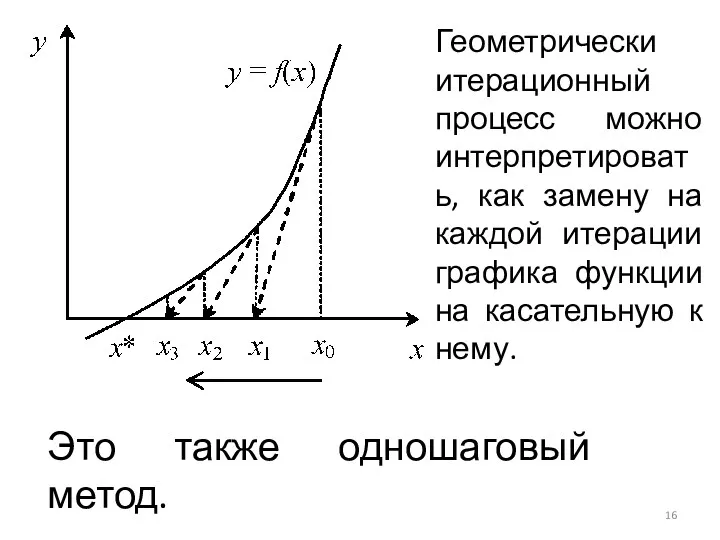
Геометрически итерационный процесс можно интерпретировать, как замену на каждой итерации графика функции на касательную к нему.
Это также одношаговый метод.

Сходимость метода определяется условием
| ϕ'(x) | = |f f ''/ f '2| < 1.
В общем случае, если нулевое приближение выбрано достаточно близко к корню, ньютоновские итерации сходятся.
Проблематичным может быть выбор начального приближения x0 в виду узости области сходимости. При выборе начального приближения х0 имеет смысл использовать заведомо сходящийся метод, например, метод деления отрезка пополам.

Задание
1. Построить график функции и определить приблизительное положение корней.
2. Составить программу на языке Java для решения уравнения (уточнения корня):
(а) методом деления отрезка пополам. Для нахождения корня следует должным образом выбрать отрезок, на котором ищется решение;
(б) методом простых итераций. Для обеспечения сходимости следует должным образом подобрать вспомогательную функцию и начальное приближение;

(в) методом Ньютона. Для обеспечения сходимости следует должным образом подобрать начальное приближение.
3. Решение получить с точностью 0.0001. Определить количество делений пополам/итераций, которое вам понадобилось для этого.