Содержание
- 2. │x – xпр │ Величину ε также называют допустимой ошибкой, которую можно задать по своему усмотрению.
- 3. Отделение корней Отделение корней можно проводить графически и аналитически. Для того чтобы графически отделить корни уравнения,
- 4. Аналитическое отделение корней основано на следующих теоремах. Теорема 1. Если непрерывная функция f(x) принимает на концах
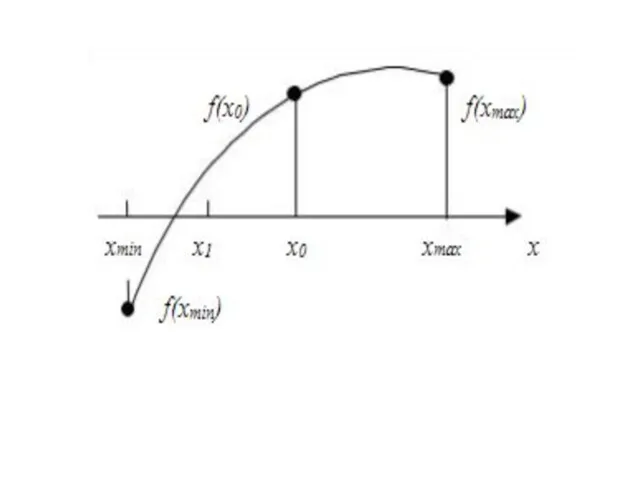
- 5. Метод половинного деления (метод дихотомии) Выбор начального приближения состоит в том, чтобы задать границы xmin и
- 7. Условие остановки итерационного процесса может быть сформулировано несколькими способами: n = nmax, где nmax - заранее
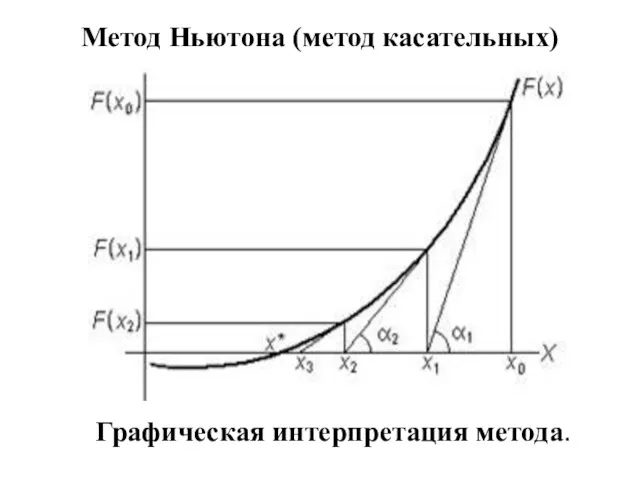
- 8. Метод Ньютона (метод касательных) Графическая интерпретация метода.
- 9. В общем случае вычислительный процесс метода Ньютона выражается формулой:
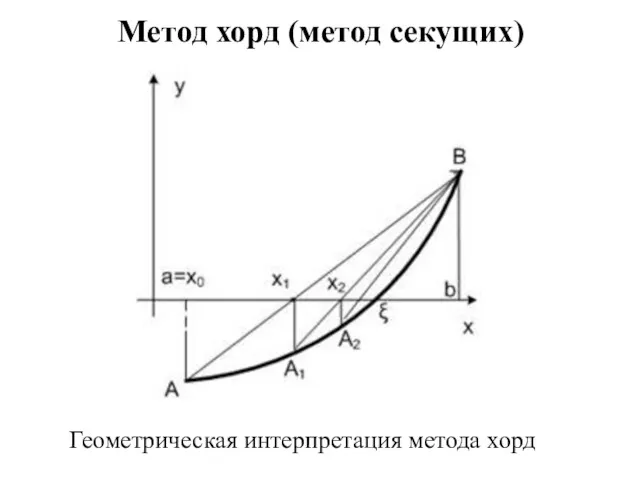
- 10. Метод хорд (метод секущих) Геометрическая интерпретация метода хорд
- 11. Положим y = 0 и найдем значение х = х1 (очередное приближение): Повторим процесс вычислений для
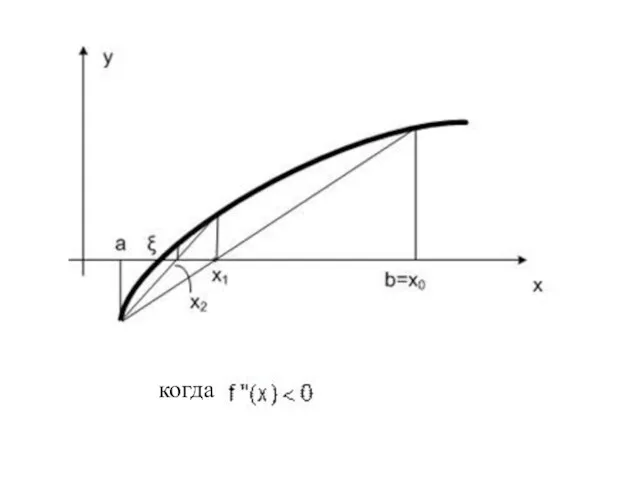
- 12. В случае расчетная формула метода хорд будет иметь вид Эта формула справедлива, когда за неподвижную точку
- 13. когда
- 14. Уравнение прямой для этого случая имеет вид Очередное приближение х1 при y = 0 Тогда формула
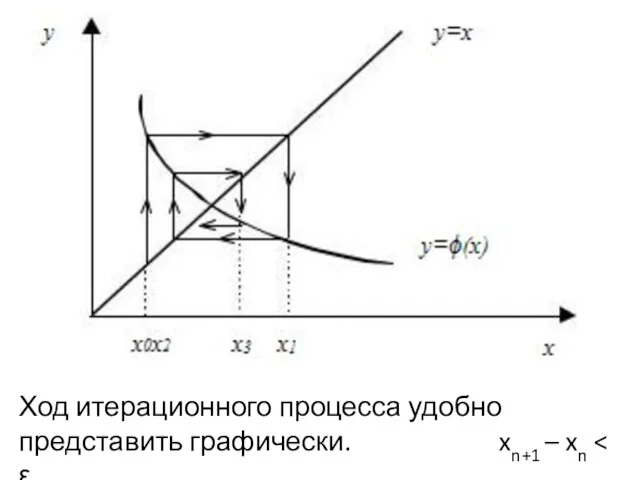
- 15. Метод простых итераций Для реализации этого метода исходное уравнение f(x)=0 предварительно преобразуется к виду x=ϕ(x). Обычно
- 16. Ход итерационного процесса удобно представить графически. xn+1 – xn
- 17. Задача численного интегрирования В ряде задач возникает необходимость вычисления определенного интеграла от некоторой функции: где f(x)
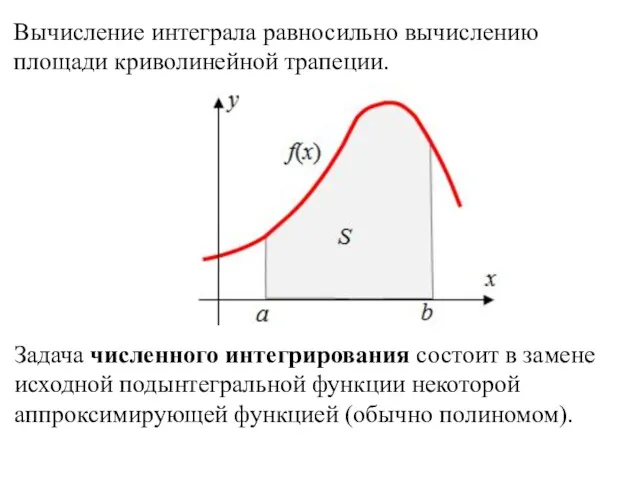
- 18. Вычисление интеграла равносильно вычислению площади криволинейной трапеции. Задача численного интегрирования состоит в замене исходной подынтегральной функции
- 19. Численное интегрирование применяется, когда: сама подынтегральная функция не задана аналитически, а например, представлена в виде таблицы
- 20. хj– узлы интегрирования Выражение называют квадратурной формулой. Разделим отрезок [a, b] на N равных частей, то
- 21. Погрешность квадратурной формулы определяется выражением: и зависит от выбора коэффициентов Сj и от расположения узлов хj
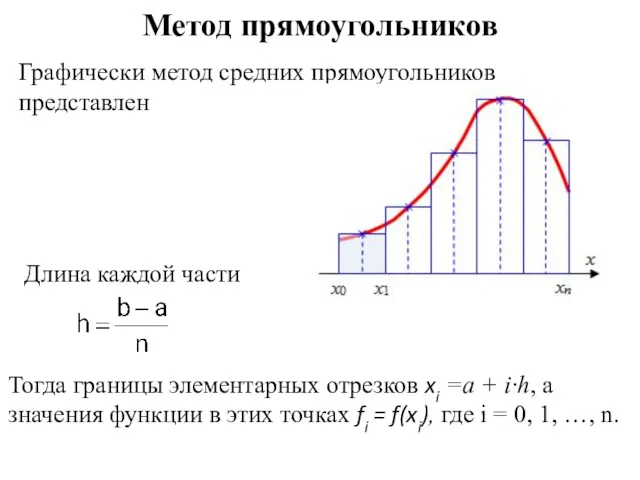
- 22. Метод прямоугольников Графически метод средних прямоугольников представлен Длина каждой части Тогда границы элементарных отрезков xi =a
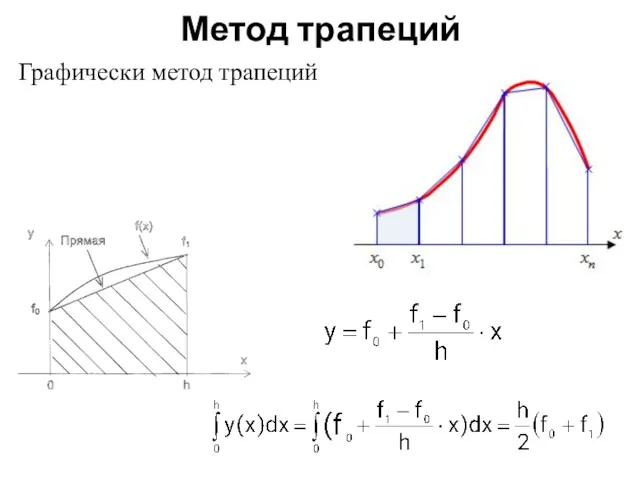
- 24. Метод трапеций Графически метод трапеций
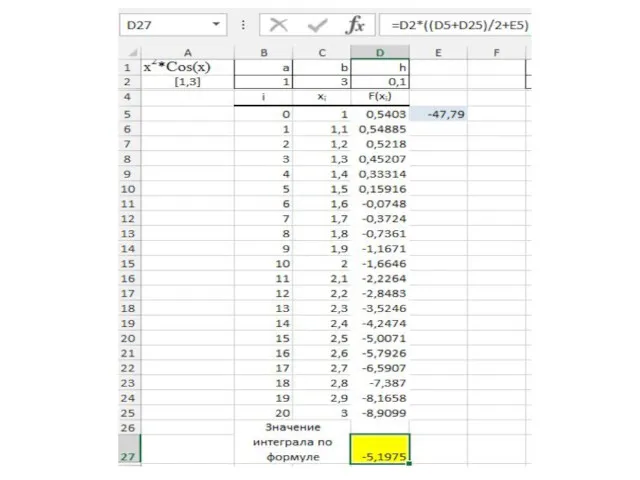
- 25. формула трапеций имеет вид Тогда границы элементарных отрезков xi =a + i*h, а значения функции в
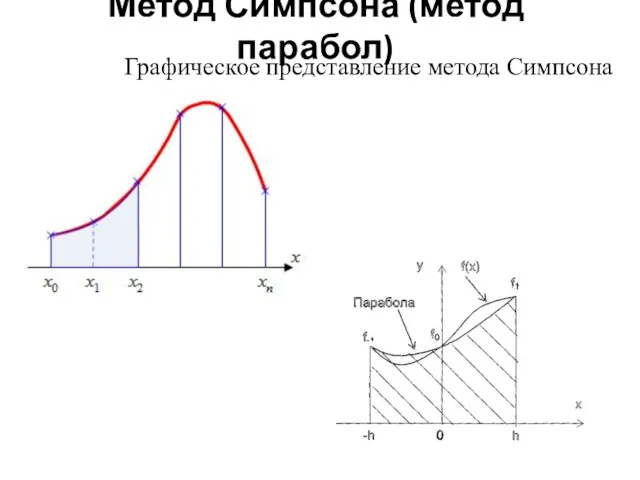
- 26. Метод Симпсона (метод парабол) Графическое представление метода Симпсона
- 27. Указанная парабола задается уравнением Тогда границы элементарных отрезков а значения функции в этих точках , где
- 28. Суммируя левую и правую части этого соотношения от до , получаем усложненную квадратурную формулу Симпсона
- 31. Скачать презентацию

















 Координаты вектора
Координаты вектора Нахождение однозначного частного путем подбора
Нахождение однозначного частного путем подбора Матриці та дії над ними
Матриці та дії над ними Дисперсиялық талдау. Крускал-Уоллис критерийі
Дисперсиялық талдау. Крускал-Уоллис критерийі фоны презентаций Диск Диск Диск Диск Диск
фоны презентаций Диск Диск Диск Диск Диск Числа от 1 до 1000. Приём письменного вычитания трёхзначных чисел
Числа от 1 до 1000. Приём письменного вычитания трёхзначных чисел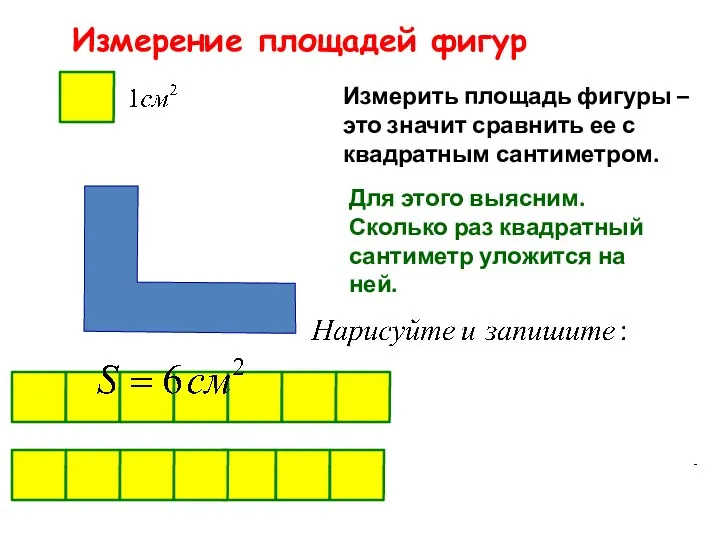 Измерение площадей фигур
Измерение площадей фигур Урок математики в 3 классе по теме: Деление двузначного числа на однозначное
Урок математики в 3 классе по теме: Деление двузначного числа на однозначное Математический тренажер по решению задач на нахождение периметра.
Математический тренажер по решению задач на нахождение периметра. Линейная регрессия
Линейная регрессия Определители
Определители Трапеция. Свойства
Трапеция. Свойства Үлес
Үлес Сыбайлас және вертикаль бұрыштар
Сыбайлас және вертикаль бұрыштар Таблица сложения с переходом через 10
Таблица сложения с переходом через 10 Страна геометрических фигур
Страна геометрических фигур Тела и поверхности вращения. Цилиндр
Тела и поверхности вращения. Цилиндр Найди значение выражений
Найди значение выражений Задание 10: Задачи с прикладным содержанием
Задание 10: Задачи с прикладным содержанием Объем цилиндрического тела. Двойной интеграл. (Лекция 2.1)
Объем цилиндрического тела. Двойной интеграл. (Лекция 2.1) Среднее арифметическое. Деление десятичной дроби на натуральное число. 5 класс
Среднее арифметическое. Деление десятичной дроби на натуральное число. 5 класс Графическое представление статистических данных
Графическое представление статистических данных Координатная плоскость
Координатная плоскость Наибольший общий делитель
Наибольший общий делитель Исчисление высказываний. Элементы теории алгоритмов
Исчисление высказываний. Элементы теории алгоритмов Отношения между множествами
Отношения между множествами Решение текстовых задач. Задачи на движение
Решение текстовых задач. Задачи на движение Функции. Основные характеристики функции. Чётность функции
Функции. Основные характеристики функции. Чётность функции