Содержание
- 2. ТИПЫ РЯДОВ Числовые ряды Функциональные ряды Знакоположительные числовые ряды Знакопеременные числовые ряды Функциональные ряды 2. Степенные
- 3. Числовые ряды Пусть члены числовой последовательности О п р е д е л е н и
- 4. О п р е д е л е н и е. Сумма первых членов ряда называется
- 5. Необходимый признак сходимости Сходимость ряда исследуется по следующей схеме: Проверяется необходимый признак сходимости. Если необходимый признак
- 6. Необходимый признак следует понимать так: Если то ряд может сходиться, но может и расходиться. Если ряд
- 7. Достаточные признаки сходимости знакоположительных рядов Числовой ряд является знакоположительным, если все его члены положительны Признак сравнения
- 8. Признак сравнения 2 (предельный) Если существует конечный, отличный от нуля предел отношения то оба ряда (1)
- 9. 2. Обобщенный гармонический ряд Если Если то ряд сходится то ряд расходится 3. Гармонический ряд ряд
- 10. Например, сходящимися рядами будут являться следующие ряды Например, расходящимися рядами будут являться следующие ряды
- 11. Признак сравнения применяется для решения вопроса о сходимости, к примеру, рядов При использовании этого признака нужно
- 12. Таблица эквивалентных бесконечно малых величин
- 13. -- ряд расходится, так как а гармонический ряд расходится. -- ряд сходится, так как а ряд
- 14. -- ряд расходится, так как члены его для достаточно больших эквивалентны членам гармонического ряда а ряд
- 15. ряд сходится как обобщенный гармонический ряд с показателем Здесь использовано то, что при ряд сходится как
- 16. ряд расходится В данном случае использовано то обстоятельство, что при ряд сходится как обобщенный гармонический ряд
- 17. ряд расходится как обобщенный гармонический с показателем Здесь использовано при ряд сходится как геометрический со знаменателем
- 18. Признак Даламбера Если в числовом знакоположительном ряде существует предел отношения последующего члена ряда к предыдущему при
- 19. Признак Даламбера применяется для решения вопроса о сходимости таких рядов, общие члены которых содержат степенные, показательные
- 20. При применении признака Даламбера может встретиться необходимость использования второго замечательного предела. Применяя признак Даламбера, необходимо: 1)
- 21. -- ряд расходится Здесь учтено, что
- 22. -- ряд сходится. Здесь учтено, что при
- 23. -- ряд расходится
- 24. -- ряд сходится
- 25. -- ряд сходится Здесь учтено, что при
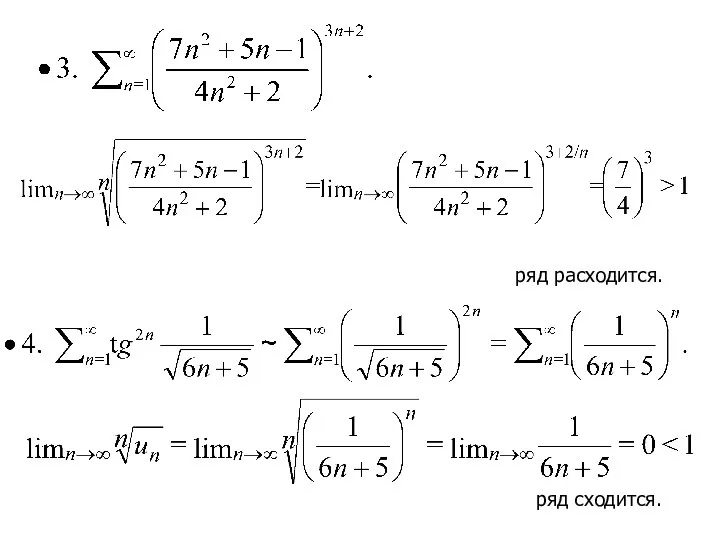
- 26. Радикальный признак Коши Если в числовом знакоположительном ряде существует предел корня ой степени из общего члена
- 27. -- ряд сходится -- ряд сходится
- 28. ряд расходится. ряд сходится.
- 29. -- ряд сходится.
- 30. ряд расходится.
- 31. Интегральный признак Коши Если при непрерывная, положительная и монотонно убывающая непрерывная, положительная и монотонно убывающая функция
- 32. Интегральный признак Коши применяется для решения вопроса о сходимости рядов типа интеграл и вместе с ним
- 33. -- ряд сходится, так как сходится несобственный интеграл
- 34. -- ряд сходится, так как сходится несобственный интеграл
- 35. -- ряд сходится, так как сходится несобственный интеграл
- 36. Знакочередующиеся ряды. Признак Лейбница. Условная и абсолютная сходимости Знакочередующимся называется числовой ряд, в котором знаки членов
- 37. Абсолютная и условная сходимости О п р е д е л е н и е. Знакочередующийся
- 38. 2. Составляем ряд из абсолютных величин членов данного знакочередующегося ряда и исследуем сходимость полученного знакоположительного ряда
- 39. -- ряд расходится, так как не выполняется признак Лейбница. -- ряд расходится, так как не выполняется
- 40. -- ряд сходится по признаку Лейбница. 2. Проверим сходимость соответствующего знакоположительного ряда -- ряд расходится. Вывод:
- 41. -- ряд сходится по признаку Лейбница. 2. Составляем ряд из абсолютных величин членов данного ряда и
- 42. ряд сходится по признаку Лейбница 2. Сходимость соответствующего знакоположительного ряда проверяем с помощью интегрального признака --
- 44. Скачать презентацию





















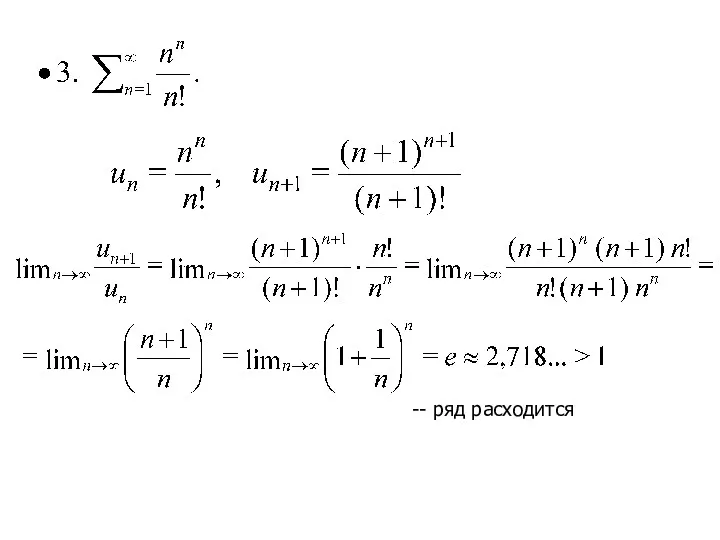




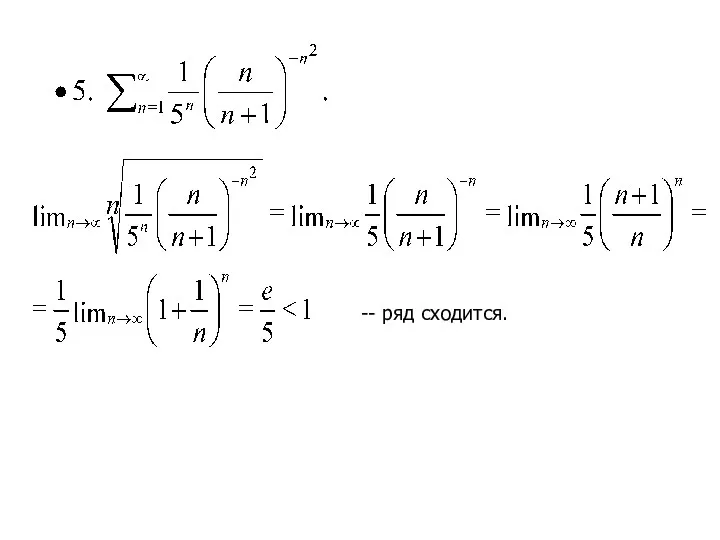













 Великая теорема Ферма
Великая теорема Ферма Элементы теории нечетких множеств
Элементы теории нечетких множеств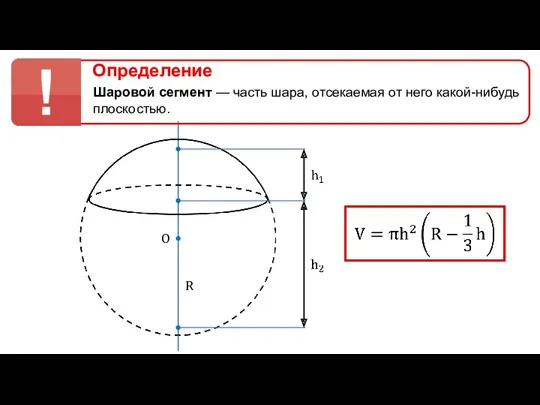 Объем частей шара
Объем частей шара Сложение отрицательных чисел» (фрагмент) для учащихся 6 класса
Сложение отрицательных чисел» (фрагмент) для учащихся 6 класса презентация по ФЕМП Первые шаги в математику
презентация по ФЕМП Первые шаги в математику Сочетательное и распределительное свойства умножения
Сочетательное и распределительное свойства умножения Тригонометрические неравенства
Тригонометрические неравенства Математика 3 класс Виды треугольников.Треугольники в архитектуре.
Математика 3 класс Виды треугольников.Треугольники в архитектуре. Аксиомы стереометрии. (10 класс)
Аксиомы стереометрии. (10 класс) Ряды Фурье. Семинар 30
Ряды Фурье. Семинар 30 Координати та вектори в просторі
Координати та вектори в просторі Презентация к уроку математики в 1 классе Присчитывание и отсчитывание по1
Презентация к уроку математики в 1 классе Присчитывание и отсчитывание по1 Урок математики по теме: Умножение и деление на 3.
Урок математики по теме: Умножение и деление на 3. Квадратный корень из степени. Упражнение 9
Квадратный корень из степени. Упражнение 9 Тіктөртбұрышты параллелепипедтің көлемі
Тіктөртбұрышты параллелепипедтің көлемі Презентация по теме: Числа от 1 до 10
Презентация по теме: Числа от 1 до 10 Одночлен и его стандартный вид
Одночлен и его стандартный вид Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20
Конспект и презентация к уроку-путешествию в лес, математика 1 класс Закрепление навыков сложения и вычитания в пределах 20 Конус. Виды конусов
Конус. Виды конусов Красота в математике или применение векторов к доказательству стереометрических теорем
Красота в математике или применение векторов к доказательству стереометрических теорем Теорема Пифагора – её история и значение
Теорема Пифагора – её история и значение Решение задач на концентрацию, смеси и сплавы
Решение задач на концентрацию, смеси и сплавы Введение в математический анализ и дифференциальное исчисление
Введение в математический анализ и дифференциальное исчисление Электронный справочник по тригонометрическим формулам
Электронный справочник по тригонометрическим формулам Доли. Обыкновенные дроби (математика, 5 класс)
Доли. Обыкновенные дроби (математика, 5 класс) День открытых дверей в 1 классе
День открытых дверей в 1 классе Решение неравенств второй степени с одной переменной
Решение неравенств второй степени с одной переменной Сложение и вычитание десятичных дробей. Решение задач
Сложение и вычитание десятичных дробей. Решение задач