Содержание
- 2. 1. Понятие производной Рассмотрим задачу о производительности труда, как пример необходимости введения понятия производной функции. Пусть
- 3. Пусть функция y=f(x) определена на промежутке Х. Возьмем любую точку х∈Х. Дадим значению х приращение Δх≠0,
- 4. Установим геометрический смысл производной. Для этого рассмотрим график функции y=f(x), определенной и непрерывной на некотором интервале
- 5. 2. Дифференцируемость функции Пусть функция y=f(x) определена на интервале (a,b), х – некоторое фиксированное значение аргумента
- 6. 3. Основные правила дифференцирования Производная функции y=f(x) может быть найдена по следующей схеме: Дадим аргументу х
- 7. Правила дифференцирования: Производная постоянной функции равна нулю, т.е. с′=0. Производная аргумента равна 1, т.е. х′=1. Производная
- 8. Пример. Найти производную функции и вычислить ее значение в точке х=1. Решение. Функцию y можно представить
- 9. 4. Производная сложной и обратной функций Пусть переменная y есть функция от переменной u (y=f(u)), а
- 10. Пример. Найти производную функции Решение. Представим , где Имеем
- 11. 7. Дифференциал функции Пусть функция y=f(x) определена на промежутке Х и дифференцируема в некоторой окрестности точки
- 12. Под дифференциалом dx независимой х понимают любое, не зависящее от х число, поэтому, по определению, дифференциалом
- 13. 8. Производные и дифференциалы высших порядков Пусть функция y=f(x) определена на отрезке (a,b). Ее производная f′(x)
- 14. Пример. Найти производные до n-го порядка включительно от функции Решение. Первая производная - вторая производная -
- 15. 9. Дифференцирование неявной функции и функции, заданной параметрически Рассмотрим дифференцирование неявной функции, заданной уравнением F(x,y)=0. Для
- 16. Иногда оказывается удобным задавать кривую не уравнением вида F(x,y)=0, а вводя третью переменную t. Совокупность двух
- 18. Скачать презентацию















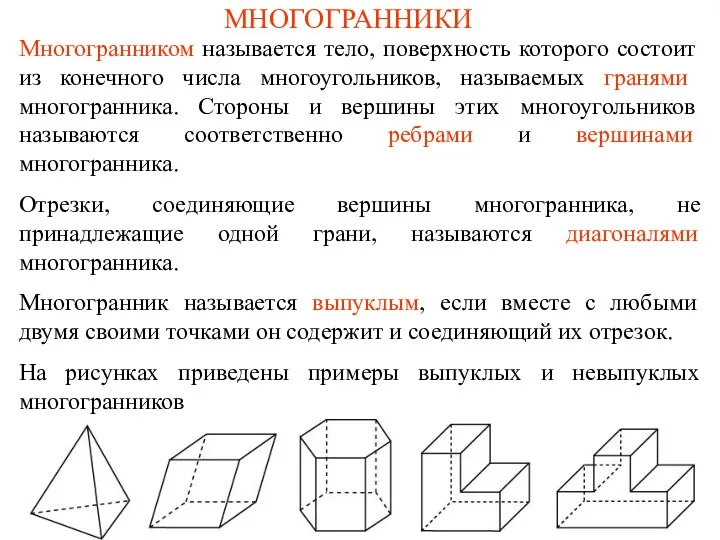 Фигуры в пространстве
Фигуры в пространстве Итоговый тест по математике
Итоговый тест по математике Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции
Обзор распространенных тестов зависимость и независимость выборок (не-) и параметрические и тесты корреляции Системы уравнений. Способы решения
Системы уравнений. Способы решения Сложение чисел с разными знаками. 6 класс
Сложение чисел с разными знаками. 6 класс Приёмы устных вычислений вида 470 + 80, 560 - 90
Приёмы устных вычислений вида 470 + 80, 560 - 90 Математика в Древнем Египте
Математика в Древнем Египте Устный счет (4 класс)
Устный счет (4 класс) Математическое странствие
Математическое странствие Типы оперирования
Типы оперирования Сложность вычислений
Сложность вычислений Time quiz
Time quiz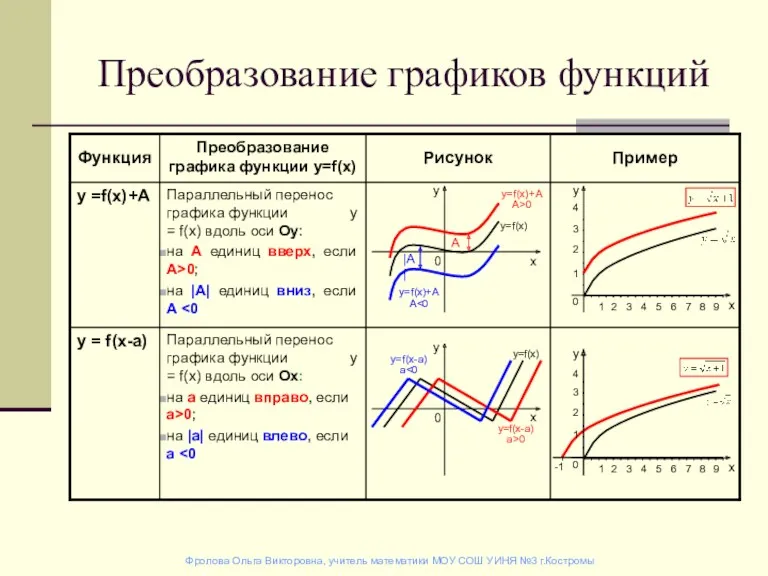 Преобразование графиков функций
Преобразование графиков функций Математика. Решение задач
Математика. Решение задач Описательные статистики
Описательные статистики Сложение и вычитание в пределах 20 (апрель 2014 год).
Сложение и вычитание в пределах 20 (апрель 2014 год). Преобразование графиков функций
Преобразование графиков функций Число и цифра 2.
Число и цифра 2. Интеллектуальный марафон
Интеллектуальный марафон Простые числа. Разложение числа на множители
Простые числа. Разложение числа на множители Решение уравнений и задач с помощью уравнений. 6 класс
Решение уравнений и задач с помощью уравнений. 6 класс Математическая сказка Диск
Математическая сказка Диск Что такое геометрия?
Что такое геометрия? Прямая и обратная пропорциональная зависимости. 6 класс
Прямая и обратная пропорциональная зависимости. 6 класс Применение теории графов к решению задач
Применение теории графов к решению задач Комбинаторные задачи. Комбинаторика
Комбинаторные задачи. Комбинаторика Сказочная страна функций. Электронный урок
Сказочная страна функций. Электронный урок Введение в Mathlab
Введение в Mathlab