Содержание
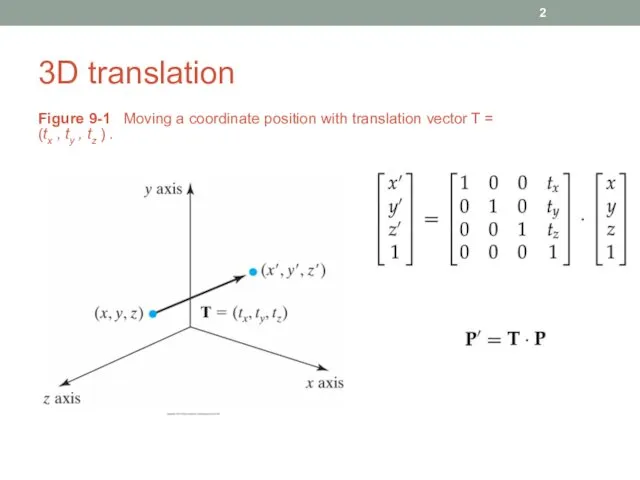
- 2. 3D translation Figure 9-1 Moving a coordinate position with translation vector T = (tx , ty
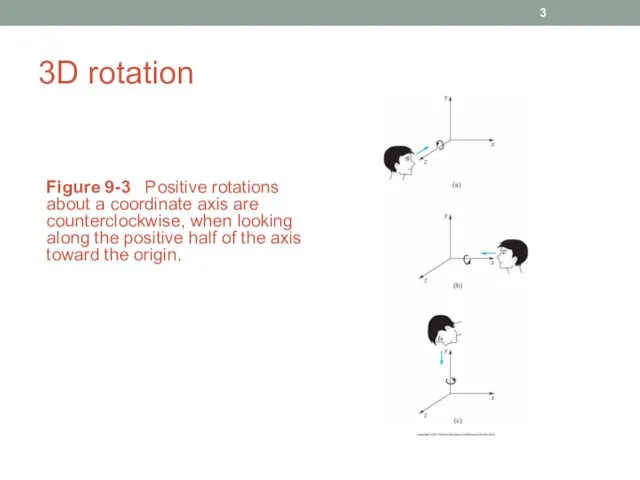
- 3. 3D rotation Figure 9-3 Positive rotations about a coordinate axis are counterclockwise, when looking along the
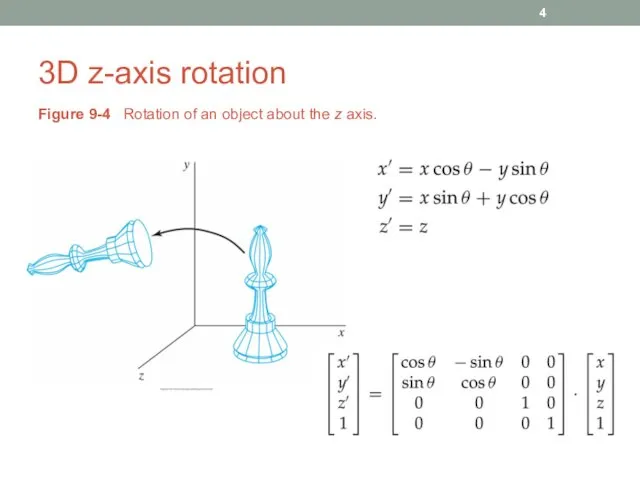
- 4. 3D z-axis rotation Figure 9-4 Rotation of an object about the z axis.
- 5. Rotations To obtain rotations about other two axes x ? y ? z ? x E.g.
- 6. General 3D rotations Figure 9-8 Sequence of transformations for rotating an object about an axis that
- 7. Arbitrary rotations Figure 9-9 Five transformation steps for obtaining a composite matrix for rotation about an
- 8. Arbitrary rotations Figure 9-10 An axis of rotation (dashed line) defined with points P1 and P2.
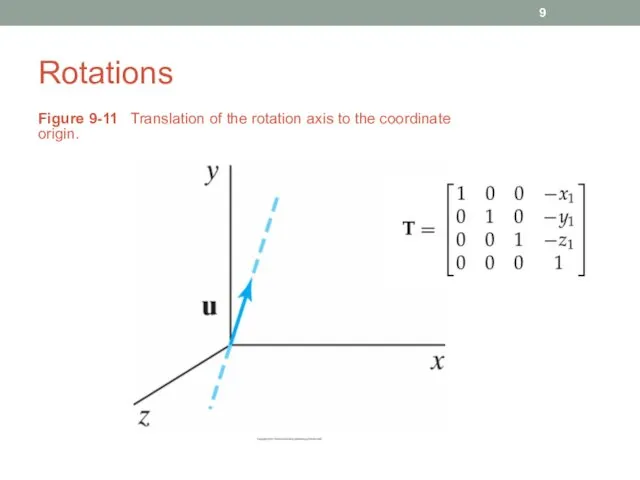
- 9. Rotations Figure 9-11 Translation of the rotation axis to the coordinate origin.
- 10. Rotations Figure 9-12 Unit vector u is rotated about the x axis to bring it into
- 11. Rotations Two steps for putting the rotation axis onto the z-axis Rotate about the x-axis Rotate
- 12. Rotations Projection of u in the yz plane Cosine of the rotation angle where Similarly, sine
- 13. Rotations Equating the right sides where |u’|=d Then,
- 14. Rotations Next, swing the unit vector in the xz plane counter-clockwise around the y-axis onto the
- 15. Rotations and so that Therefore
- 16. Rotations Together with
- 17. In general Figure 9-15 Local coordinate system for a rotation axis defined by unit vector u.
- 18. Quaternions Scalar part and vector part Think of it as a higher-order complex number Rotation about
- 19. Quaternions The rotation of the point P is carried out with quaternion operation where This produces
- 20. Quaternions Using With u=(ux, uy, uz), we finally have About an arbitrarily placed rotation axis: Quaternions
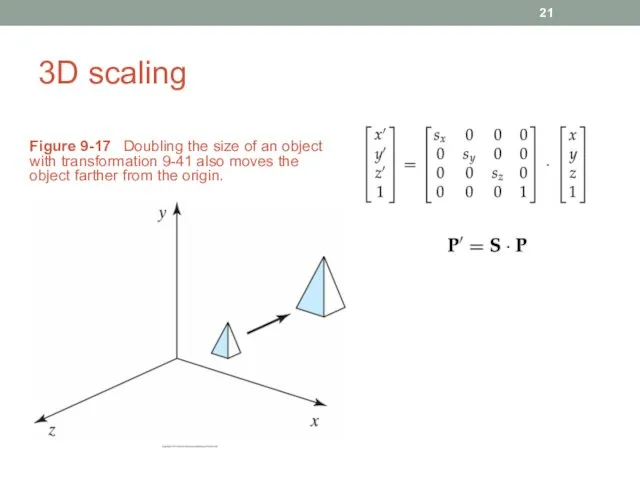
- 21. 3D scaling Figure 9-17 Doubling the size of an object with transformation 9-41 also moves the
- 22. 3D scaling Figure 9-18 A sequence of transformations for scaling an object relative to a selected
- 23. Composite 3D transformation example
- 25. Скачать презентацию

















 Презентация к уроку математики 2 класс по УМКШкола России
Презентация к уроку математики 2 класс по УМКШкола России Определение производной. Задачи, приводящие к понятию производной
Определение производной. Задачи, приводящие к понятию производной Урок по теме Число и цифра ноль.
Урок по теме Число и цифра ноль. Приёмы письменного умножения в пределах 1000
Приёмы письменного умножения в пределах 1000 Сумма нескольких слагаемых
Сумма нескольких слагаемых Свойства правильных многогранников и их применение
Свойства правильных многогранников и их применение Решение задач на составление уравнений
Решение задач на составление уравнений Теорема Пифагора
Теорема Пифагора знакомство с 0.
знакомство с 0. Решение задач на проценты. Урок математики в 5 классе
Решение задач на проценты. Урок математики в 5 классе Презентация к уроку математики 4 класс УМК Школа России М.И. Морро, М.А. Бантова
Презентация к уроку математики 4 класс УМК Школа России М.И. Морро, М.А. Бантова Теорема Пифагора – её история и значение
Теорема Пифагора – её история и значение Длина окружности. Площадь круга
Длина окружности. Площадь круга Призма
Призма Умножение смешанных чисел
Умножение смешанных чисел Сравнение углов наложением
Сравнение углов наложением построение модели по заданному силуэту (часть 2 и 3)
построение модели по заданному силуэту (часть 2 и 3) Золотое сечение и числа Фибоначчи
Золотое сечение и числа Фибоначчи Что такое координаты. 6 класс
Что такое координаты. 6 класс Прогнозирование последовательностей и принципы построения информационно-аналитических систем
Прогнозирование последовательностей и принципы построения информационно-аналитических систем Круг, окружность. Урок математики для учащихся 4 класса
Круг, окружность. Урок математики для учащихся 4 класса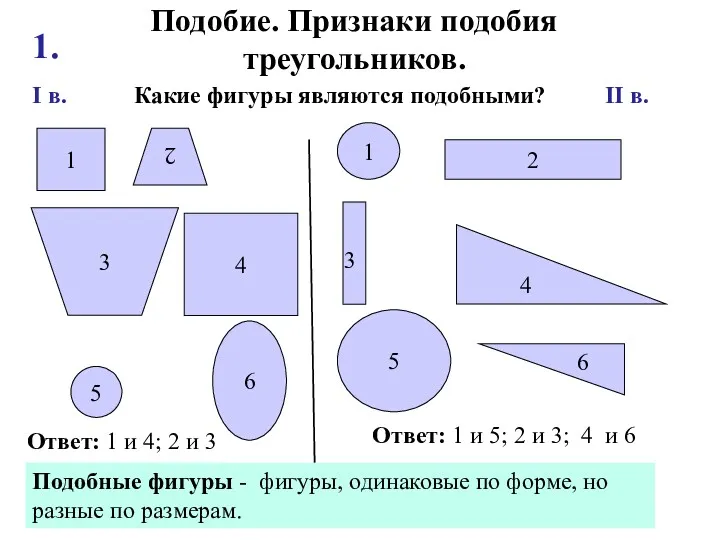 Подобие. Признаки подобия треугольников
Подобие. Признаки подобия треугольников Порівняння чисел в межах 9. (1 клас)
Порівняння чисел в межах 9. (1 клас) Измерение отрезков и углов
Измерение отрезков и углов Теоремы треугольника
Теоремы треугольника Ряды динамики
Ряды динамики Двоичная система счисления
Двоичная система счисления Разработка открытого урока математики
Разработка открытого урока математики