Содержание
- 2. 1 The Determinant of a Matrix 2 Properties of Determinants 3 Application of Determinants: Cramer’s Rule
- 3. 3. 1 The Determinant of a Matrix
- 4. Determinant - a square array of numbers or variables enclosed between parallel vertical bars. **To find
- 5. Given a square matrix A its determinant is a real number associated with the matrix. The
- 6. 3. ※ The determinant is NOT a matrix operation ※ The determinant is a kind of
- 7. 3. The determinant of a 2 × 2 matrix: Note: 1. For every SQUARE matrix, there
- 8. 3. Historically speaking, the use of determinants arose from the recognition of special patterns that occur
- 9. det = = (1)(4) – (2)(3) = -2 Determinants 2x2 examples Note: The determinant of a
- 10. Determinants M11 = 2 7 3 0 M11 : remove row 1, col 1 To define
- 11. M12 = -1 2 3 0 M12 : remove row 1, col 2 Determinants To define
- 12. M13 = -1 2 2 7 M13 : remove row 1, col 3 Determinants To define
- 13. -2 M21 = 1 7 -2 0 M21 : remove row 2, col 1 Determinants To
- 14. -2 M22 = 1 2 -2 0 M22 : remove row 2, col 2 Determinants To
- 15. -2 M23 = 1 2 1 7 M23 : remove row 2, col 3 Determinants To
- 16. -2 M31 = 1 2 -2 3 M31 : remove row 3, col 1 Determinants To
- 17. -2 M32 = 1 -1 -2 3 M32 : remove row 3, col 2 Determinants To
- 18. -2 M33 = 1 -1 1 2 M33 : remove row 3, col 3 Determinants To
- 19. For a matrix Its determinant is given by |A| = a11|M11| - a12|M12| + a13|M13| The
- 20. For a matrix Its determinant is given by |A| = a11|M11| - a12|M12| + a13|M13| From
- 21. For a matrix Its determinant is given by |A| = a11|M11| - a12|M12| + a13|M13| From
- 22. = 1x(-21) -1x(-6) +(-2)x(-11) = 7 |A| = 1x|M11| - 1x|M12| + (-2)x|M13| 3x3 Example
- 23. = 0x(-2) -1x(1) +(3)x(13) = 38 |B| = 0x|M11| - 1x|M12| + 3x|M13| 3x3 Example
- 24. For the matrix We used the top row to calculate the determinant: |A| = a11|M11| -
- 25. For the matrix Using the top row: |A| = a11|M11| - a12|M12| + a13|M13| Using the
- 26. |A| = a11|M11| - a12|M12| + a13|M13| Notice the changing signs depending on what row we
- 27. Equally, we could have used any column as long as we follow the signs pattern E.g.
- 28. This choice sometimes makes it a bit easier to calculate determinants. e.g. = 1x(-1) -1x(0) +
- 29. This choice sometimes makes it a bit easier to calculate determinants. e.g.
- 30. For a 4x4 matrix we add up minors like the 3x3 case, and again use the
- 31. A general formula for determinants
- 32. 3.
- 33. 3. Minor of the entry aij: the determinant of the matrix obtained by deleting the i-th
- 34. 3. Ex: Notes: Sign pattern for cofactors. Odd positions (where i+j is odd) have negative signs,
- 35. 3. Theorem: Expansion by cofactors (cofactor expansion along the i-th row, i=1, 2,…, n) (cofactor expansion
- 36. 3. Ex: The determinant of a square matrix of order 3
- 37. 3. Ex: The determinant of a square matrix of order 3 Sol:
- 38. 3. Ex: The determinant of a square matrix of order 4
- 39. 3. Sol: ※ By comparing the exercises, it is apparent that the computational effort for the
- 40. 3. Upper triangular matrix: Lower triangular matrix: Diagonal matrix: All entries below the main diagonal are
- 41. 3. Theorem: (Determinant of a Triangular Matrix) If A is an n × n triangular matrix
- 42. 3. Ex: Find the determinants of the following triangular matrices (a) (b) |A| = (2)(–2)(1)(3) =
- 43. 3. Conditions that yield a zero determinant (a) An entire row (or an entire column) consists
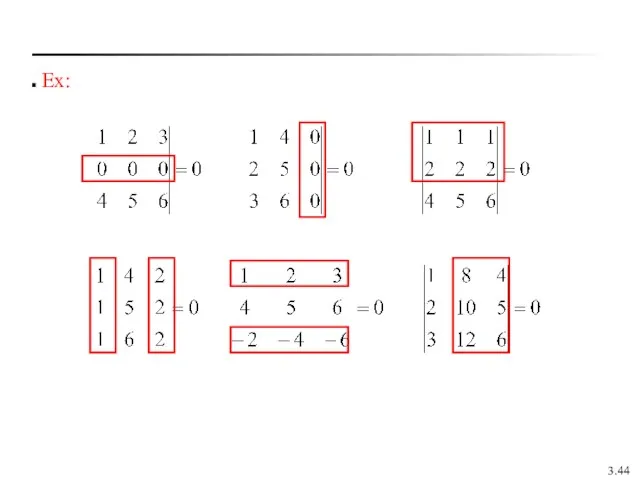
- 44. 3. Ex:
- 45. 3. Notes: Theorem: Determinant of a matrix product (2) (3) det(AB) = det(A) det(B) (Verified by
- 46. 3. Ex 1: The determinant of a matrix product Sol: Find |A|, |B|, and |AB|
- 47. 3. |AB| = |A| |B| Check:
- 48. 3. Ex 2: Sol: Theorem: Determinant of a scalar multiple of a matrix If A is
- 49. 3. Theorem: (Determinant of an invertible matrix) A square matrix A is invertible (nonsingular) if and
- 50. 3. Ex 3: Classifying square matrices as singular or nonsingular A has no inverse (it is
- 51. Inverse Matrices 3.
- 52. Theorem of Inverse Matrices 3.
- 53. 3.
- 54. 3.
- 55. 3.
- 56. Example 3 3.
- 57. 3.
- 58. 3. Ex 4: (a) (b) Sol: Theorem: Determinant of an inverse matrix Theorem: Determinant of a
- 59. 3. The similarity between the noninvertible matrix and the real number 0
- 60. 3. If A is an n × n matrix, then the following statements are equivalent (1)
- 61. 3. Ex 5: Which of the following system has a unique solution? (a) (b)
- 62. 3. Sol: (a) This system does not have a unique solution (b) This system has a
- 63. 3. Theorem: Cramer’s Rule A(i) represents the i-th column vector in A 3 Applications of Determinants
- 64. 3.
- 65. 3. Ex: Use Cramer’s rule to solve the system of linear equation Sol:
- 67. Скачать презентацию































































 Круги Эйлера
Круги Эйлера Каталог авторских дидактических материалов по интерактивному оборудованию
Каталог авторских дидактических материалов по интерактивному оборудованию Обобщающий урок по теме: Треугольники
Обобщающий урок по теме: Треугольники Деление с остатком
Деление с остатком Декадник наук 2 класс
Декадник наук 2 класс Задачі на визначення, на скільки коротший. Обчислення значень виразів
Задачі на визначення, на скільки коротший. Обчислення значень виразів Свойства биссектрис треугольника. Тематическая подготовка к ОГЭ
Свойства биссектрис треугольника. Тематическая подготовка к ОГЭ Вычитание вида 12 -
Вычитание вида 12 - Презентация к уроку по математике
Презентация к уроку по математике Число и цифра 8.
Число и цифра 8. Координатная плоскость
Координатная плоскость Теорема Фалеса
Теорема Фалеса Урок математики во 2 классе МСКОУ СКОШ VIII вида Решение задач
Урок математики во 2 классе МСКОУ СКОШ VIII вида Решение задач введение вероятностно-статестической линиии в школьный курс математики 5 - 6 классов
введение вероятностно-статестической линиии в школьный курс математики 5 - 6 классов Виды углов в треугольнике
Виды углов в треугольнике Площадь прямоугольника. Площадь параллелограмма и ромба
Площадь прямоугольника. Площадь параллелограмма и ромба Пропорциональные отрезки в прямоугольном треугольнике (урок-квест)
Пропорциональные отрезки в прямоугольном треугольнике (урок-квест) Декартові координати у просторі
Декартові координати у просторі Что узнали и чему научились. Математика, 4 класс
Что узнали и чему научились. Математика, 4 класс Функция корень из х. Ее свойства и график
Функция корень из х. Ее свойства и график Ключевые слова и понятия по теме: Алгебра логики
Ключевые слова и понятия по теме: Алгебра логики Степень с натуральным показателем и её свойства (7 класс)
Степень с натуральным показателем и её свойства (7 класс) Статистичні показники
Статистичні показники Метод координат
Метод координат Алгоритм и его формальное исполнение. Типы алгоритмических структур
Алгоритм и его формальное исполнение. Типы алгоритмических структур Площадь трапеции. Задачи
Площадь трапеции. Задачи Презентации к урокам математики
Презентации к урокам математики Окружности. Внутреннее сопряжение. Вспомогательная дуга. Сопрягающая дуга
Окружности. Внутреннее сопряжение. Вспомогательная дуга. Сопрягающая дуга