Действительные числа. Степенная функция. Материалы по математике для обучающихся 10-11 класса презентация
Содержание
- 2. Действительным числом называется бесконечная десятичная дробь вид а , где - целое число, а каждая из
- 3. Бесконечно убывающая геометрическая прогрессия. Определение: Числовая последовательность, первый член которой отличен от нуля, а каждый последующий
- 4. Пример. Выяснить, является ли геометрическая прогрессия бесконечно убывающей: Решение: Так как знаменатель геометрической прогрессии меньше 1,
- 5. Арифметический корень натуральной степени. Определение: Арифметическим корнем натуральной степени п ≥ 2 из неотрицательного Числа а
- 6. Примеры:
- 7. Тождественные преобразования выражений с арифметическим корнем натуральной степени: примеры заданий из Открытого Банка Задач Единого Государственного
- 8. Степень с рациональным показателем. Если п – натуральное число, m – целое число, то при а
- 9. Свойства степени с рациональным показателем. Рассмотрим свойства степени с рациональным показателем, они аналогичны свойствам степени с
- 10. Свойства степени с рациональным показателем. m и n- рациональные числа: Можно разделить степени с одинаковым основанием,
- 11. Свойства степени с рациональным показателем. m и n- рациональные числа: Для того чтобы степень возвести в
- 12. Свойства степени с рациональным показателем. m и n- рациональные числа: При умножении степеней с одинаковым показателем,
- 13. Свойства степени с рациональным показателем. m и n- рациональные числа: Чтобы разделить степени с одинаковыми показателями,
- 14. Примеры решения заданий из Открытого Банка Задач Единого Государственного Экзамена по математике
- 15. Задания для самостоятельной работы. Выполните упражнение № 57- 60 на странице 31 учебника. 2. Вычислите значения
- 16. Домашняя работа №-57 1) 2) 3) 4) 5) 6)
- 17. Домашняя работа №-58 1) 2) 3) 4) 5)
- 18. Домашняя работа №-59 1) 2) 3) 4)
- 19. Домашняя работа №-60: 1) 2) 3) 4)
- 20. Домашняя работа №-68: 1) 2) 3) 4)
- 21. Домашняя работа №-69: 1) 2) 3) 4)
- 22. Домашняя работа №-70: 1) 2) 3) 4)
- 23. Иррациональное уравнение. Определение: уравнение, содержащее неизвестную величину под знаком корня (радикала), называется иррациональным.
- 25. Скачать презентацию






















 Умножение и деление смешанных дробей
Умножение и деление смешанных дробей Эконометрика. Обобщенный метод наименьших квадратов
Эконометрика. Обобщенный метод наименьших квадратов Треугольник. Четырехугольник. Окружность. Путешествие в геометрию
Треугольник. Четырехугольник. Окружность. Путешествие в геометрию Применение производной и первообразной показательной и логарифмической функции
Применение производной и первообразной показательной и логарифмической функции Неравенства
Неравенства Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке
Нахождение наибольшего и наименьшего значений непрерывной функции на промежутке Величины 1 класс
Величины 1 класс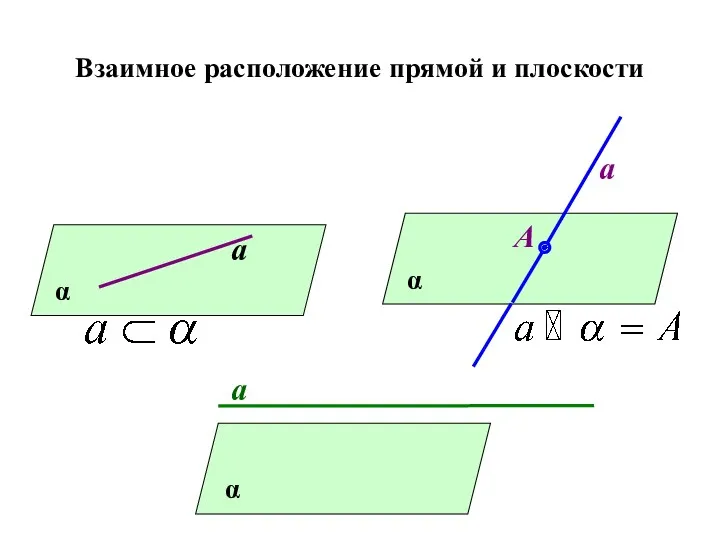 Взаимное расположение прямой и плоскости
Взаимное расположение прямой и плоскости 20231001_mnogougolniki
20231001_mnogougolniki Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени
Сложение и вычитание чисел, полученных при измерении одной, двумя единицами времени Презентация Путешествие в страну дробей
Презентация Путешествие в страну дробей Первый признак равенства треугольников. 7 класс
Первый признак равенства треугольников. 7 класс Как правильно писать цифры
Как правильно писать цифры Элементы теории вероятностей
Элементы теории вероятностей Наибольшее и наименьшее значения функции
Наибольшее и наименьшее значения функции Тренировочная работа № 3
Тренировочная работа № 3 Площади. Равновеликие фигуры
Площади. Равновеликие фигуры Представление натуральных чисел на координатном луче
Представление натуральных чисел на координатном луче Скорость, время, расстояние. Математика, 4класс.
Скорость, время, расстояние. Математика, 4класс. ГИА - 2016. Открытый банк заданий по математике. Задача №9. Вычисление углов
ГИА - 2016. Открытый банк заданий по математике. Задача №9. Вычисление углов Цилиндр. Площадь поверхности цилиндра
Цилиндр. Площадь поверхности цилиндра Геометрические фигуры
Геометрические фигуры Математика. 1 класс. Урок 4. Признаки предметов
Математика. 1 класс. Урок 4. Признаки предметов Задача по финансовой математике
Задача по финансовой математике Правильный додекаэдр
Правильный додекаэдр Геометрические фигуры (презентация для подготовки)
Геометрические фигуры (презентация для подготовки) Вклад математиков в победу Великой Отечественной Войне
Вклад математиков в победу Великой Отечественной Войне Конспект урока математики (+ презентация). 4 класс
Конспект урока математики (+ презентация). 4 класс