Слайд 2

Определение производной.
Пусть функция у = f(х) определена на промежутке X.
Возьмем точку х Х Дадим значению х приращение Δх ≠ 0, тогда функция получит приращение
Δ y = f(х+ Δх)-f(х).
Определение. Производной функции
у = f(х) называется предел отношения приращения функции к приращению независимой переменной при стремлении последнего к нулю (если этот предел существует):
Слайд 3

y′= =
Производная обозначается …
Нахождение производной называется дифференцированием этой функции
Слайд 4

Зависимость между непрерывностью функции и дифференцируемостью.
Теорема. Если функция у =
f(х) дифференцируема в точке х0, то она в этой точке непрерывна.
Слайд 5

Производные:
Постоянной величины
Аргумента;
Суммы;
Произведения;
Частного;
Сложной функции
Таблица производных.
Производные высших порядков.
Слайд 6

Основные теоремы дифференциального исчисления
Теорема Ферма. Если дифференцируемая на промежутке X
функция y=f(x) достигает наибольшего или наименьшего значения во внутренней точке х0 этого промежутка, то производная функции в этой точке равна нулю, т.е.
f' (х0) = 0.
Слайд 7

Теорема Лагранжа. Пусть функция у = f(х) удовлетворяет следующим условиям
непрерывна на
отрезке [а, b];
дифференцируема на интервале
(а, b);
Тогда внутри отрезка существует по крайней мере одна такая точка
ξ (а, b), в которой производная равна частному от деления приращения функции на приращение аргумента на этом отрезке,
Слайд 8
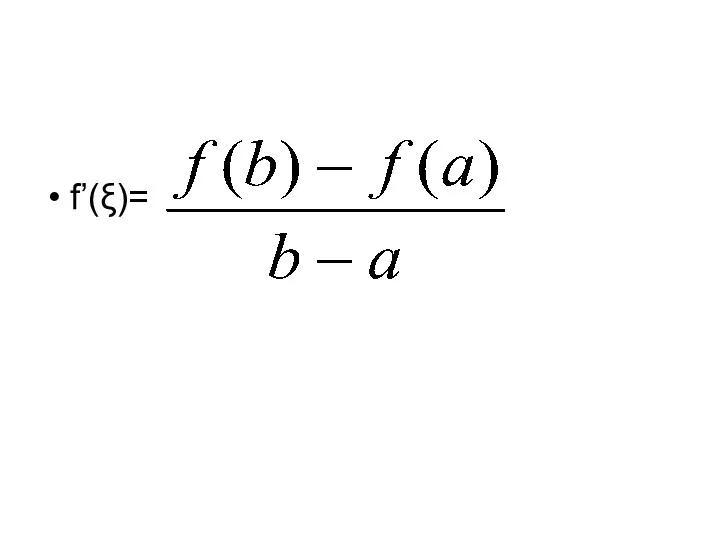
f’(ξ)=
Слайд 9

Правило Лопиталя
Теорема. Предел отношения двух бесконечно малых или бесконечно больших функций
равен пределу отношения их производных {конечному или бесконечному), если последний существует в указанном смысле.
Слайд 10
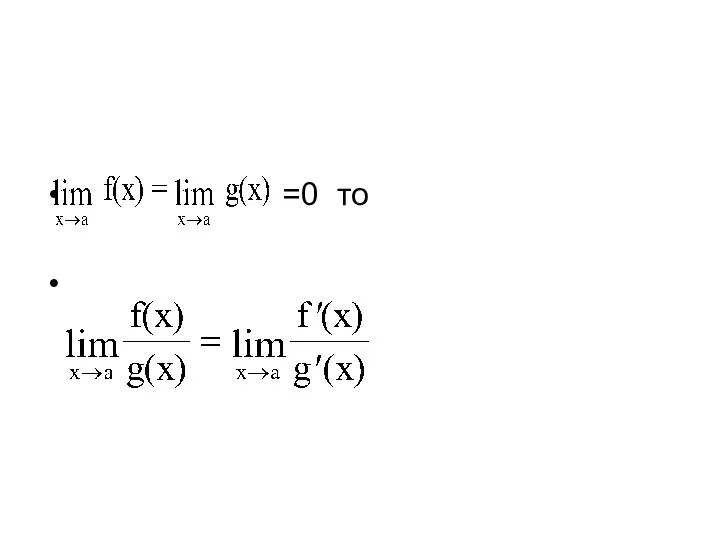
=0 то
Слайд 11

Возрастание и убывание функций
Теорема (достаточное условие возрастания функции). Если производная
дифференцируемой функции положительна внутри некоторого промежутка X, то функция возрастает на этом промежутке.
Слайд 12

Теорема (достаточное условие убывания функции). Если производная дифференцируемой функции отрицательна внутри
некоторого промежутка X, то она убывает на этом промежутке.
Слайд 13

Экстремум функции
Определение 1. Точка х0 называется точкой максимума функции f(x),
если в некоторой окрестности точки х0 выполняется неравенство f(x) <=f(x0)
Определение 2. Точка х1 называется точкой минимума функции f(x), если в некоторой окрестности точки х1 выполняется неравенство f(x) >=f(x1)
Слайд 14

Необходимое условие экстремума.
Для того, чтобы функция у =f(x) имела экстремум
в точке х0, необходимо, чтобы ее производная в этой точке равнялась нулю (f'(x0) = 0) или не существовала.
Слайд 15

Первое достаточное условие экстремума.
Теорема. Если при переходе через точку х0 производная
дифференцируемой функции y=f(x) меняет свой знак с плюса на минус, то точка х0 есть точка максимума функции у = f(х), а если с минуса на плюс, то точка минимума.
Слайд 16

Схема исследования функции y=f(х) на экстремум.
1°. Найти производную у '=f'(х).
2°. Найти
критические точки функции, в которых производная f'(х)=0 или не существует.
3°. Исследовать знак производной слева и справа от каждой критической точки и сделать вывод о наличии экстремумов функции.
4°. Найти экстремумы (экстремальные значения) функции.
Слайд 17

Второе достаточное условие экстремума.
Теорема. Если первая производная f‘(х) дважды дифференцируемой функции
равна нулю в некоторой точке х0, а вторая производная в этой точке
f" (х0) положительна, то х0 есть точка минимума функции f (х);
если f"(х0) отрицательна, то х0 - точка максимума.
Слайд 18

Выпуклость функции. Точки перегиба
Функция y=f(x) называется выпуклой вниз на промежутке Х,
если для любых двух значений х1,х2 X из этого промежутка выполняется неравенство
Слайд 19

Функция y=f(x) называется выпуклой вверх на промежутке Х, если для любых
двух значений х1,х2 X из этого промежутка выполняется неравенство
Слайд 20

Теорема. Функция выпукла вниз(вверх) на промежутке X тогда и только тогда,
если ее первая производная на этом промежутке монотонно возрастает (убывает).
Теорема. Если вторая производная дважды дифференцируемой функции положительна (отрицательна) внутри некоторого промежутка X, то функция выпукла вниз (вверх) на этом промежутке.
Слайд 21

Определение. Точкой перегиба графика непрерывной функции называется точка, разделяющая интервалы, в
которых функция выпукла вниз и вверх.
Теорема. Необходимое условие перегиба. Вторая производная f′′(x) дважды дифференцируемой функции в точке перегиба x0 равна нулю.
Теорема. Достаточное условие перегиба. Если вторая производная f′′(x) при переходе через некоторую точку X0 меняет свой знак, то X0 точка перегиба.
Слайд 22

Схема исследования функции на выпуклость и точки перегиба.
Найти вторую производную функции.
Найти
точки в которых f′′(x)=0 или не существует.
Исследовать знак f′′(x) слева и справа от найденных точек.
Найти значения функции в точках прегиба.
Слайд 23

Асимптоты графика функции
Асимптотой графика функции y=f(x) называется такая прямая, расстояние от
точки (X, f(x)) до этой прямой стремится к нулю при неограниченном удалении точки графика от начала координат.
Слайд 24

При исследовании функций и построении их графиков рекомендуется использовать следующую схему:
1°.
Найти область определения функции.
2°. Исследовать функцию на четность - нечетность.
3°. Найти вертикальные асимптоты.
4°. Исследовать поведение функции в бесконечности, найти горизонтальные или наклонные асимптоты.
Слайд 25

5°. Найти экстремумы и интервалы монотонности функции.
6°. Найти интервалы выпуклости функции
и точки перегиба.
7°. Найти точки пересечения с осями координат и, возможно, некоторые дополнительные точки, уточняющие график.






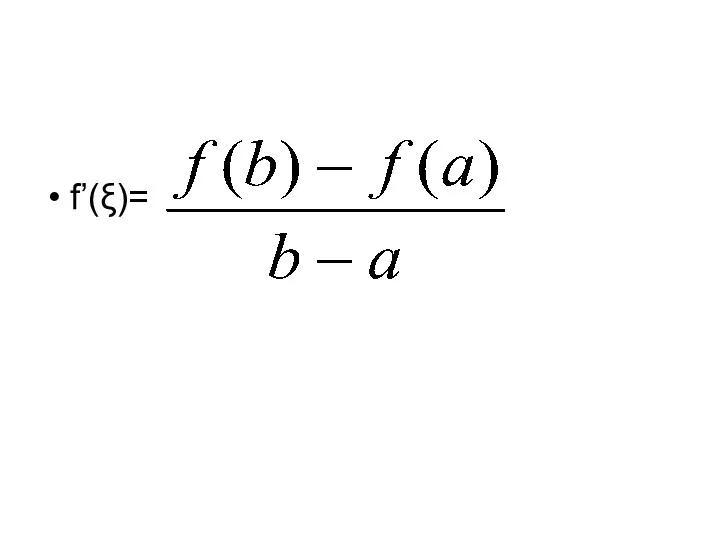

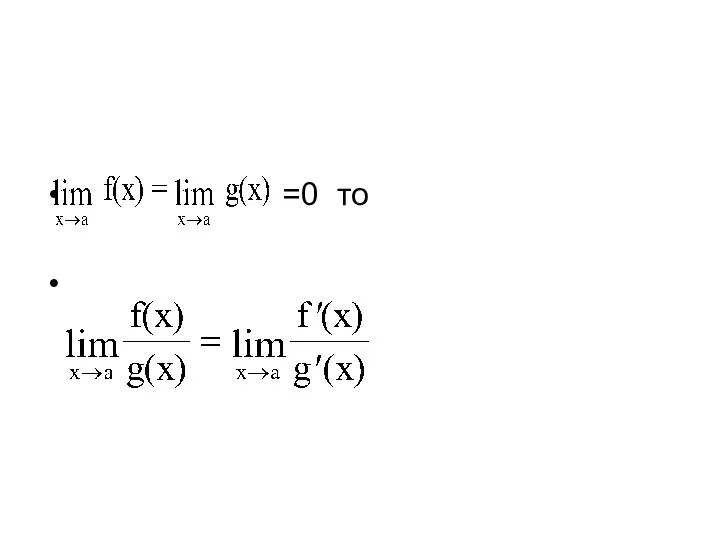















 Преобразование выражений, содержащих квадратные корни
Преобразование выражений, содержащих квадратные корни Действия с дробями
Действия с дробями Теорема Виета. Алгебра 8 класс
Теорема Виета. Алгебра 8 класс Умножение целых чисел
Умножение целых чисел Задачи на деление
Задачи на деление Умножение десятичных дробей
Умножение десятичных дробей Вычисление интегралов
Вычисление интегралов Сложение и вычитание смешанных дробей. Урок математики в 5 классе
Сложение и вычитание смешанных дробей. Урок математики в 5 классе Полезные функции Matlab’a
Полезные функции Matlab’a Решение дробно-рациональных уравнений с параметром
Решение дробно-рациональных уравнений с параметром Знакомство с приёмами умножения и деления на 10. 2 класс
Знакомство с приёмами умножения и деления на 10. 2 класс Медианы, биссектрисы и высоты треугольника
Медианы, биссектрисы и высоты треугольника Система счисления — совокупность приемов и правил записи числовой информации с помощью некоторого алфавита
Система счисления — совокупность приемов и правил записи числовой информации с помощью некоторого алфавита Вычисление степени с целым отрицательным показателем
Вычисление степени с целым отрицательным показателем Варряд
Варряд Знакомство с числами 2-го десятка. Состав чисел
Знакомство с числами 2-го десятка. Состав чисел Нахождение числа по заданному значению его дроби
Нахождение числа по заданному значению его дроби Решение задач по теме Призма. Площадь поверхности призмы 10 класс
Решение задач по теме Призма. Площадь поверхности призмы 10 класс Презентация к уроку математики Числа от 10 до 20
Презентация к уроку математики Числа от 10 до 20 урок математики по теме Выражения 1 класс
урок математики по теме Выражения 1 класс Умножение десятичных дробей
Умножение десятичных дробей Тригонометрические формулы
Тригонометрические формулы Thinking skills
Thinking skills Основные формулы метода координат в пространстве. Урок №1. 11 класс
Основные формулы метода координат в пространстве. Урок №1. 11 класс Урок математики Знакомство с действием вычитания
Урок математики Знакомство с действием вычитания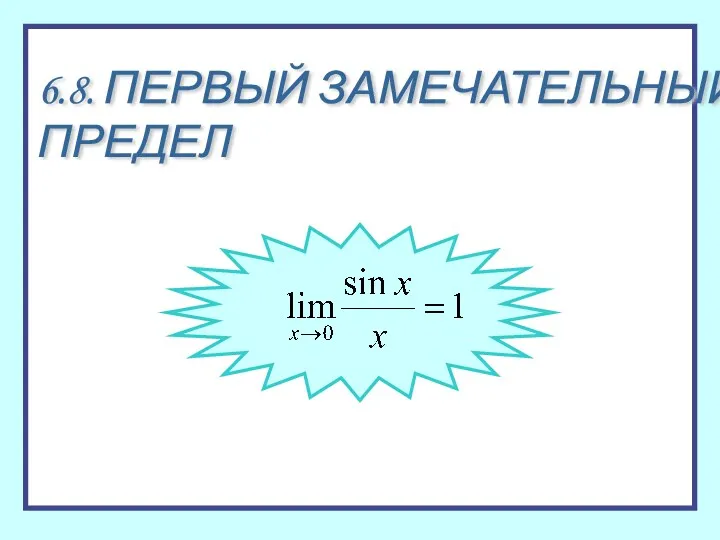 Первый замечательный предел
Первый замечательный предел Золотое сечение
Золотое сечение Угол между скрещивающимися прямыми
Угол между скрещивающимися прямыми