Дифференциальные уравнения и ряды. Знакочередующиеся и знакопеременные ряды. Ряды с комплексными членами презентация
Содержание
- 2. § 3. Знакочередующиеся и знакопеременные ряды. Ряды с комплексными членами Знакочередующимся рядом называется ряд вида: (*)
- 3. Следствие. Абсолютная погрешность при приближенном вычислении суммы сходящегося знакочередующегося ряда по абсолютной величине не превышает абсолютной
- 4. Пример 1. Вычислить приближенно сумму ряда заменив ее суммой четырех членов; оценить абсолютную погрешность. Решение. Находим
- 5. Пример 2. Вычислить с точность ε = 0,001 сумму ряда Решение. Вычисляем значения членов ряда до
- 6. Ряд а1 + а2 + а3 +…+ аn +…, члены которого имеют произвольный знак (аn >
- 7. Теорема 2 (достаточный признак сходимости знакопеременного ряда). Если ряд, составленный из абсолютных величин членов знакопеременного ряда
- 8. Пример 3. Исследовать сходимость знакопеременного ряда Решение. Проверим ряд на абсолютную сходимость. Для этого составим ряд
- 9. Пример 4. Исследовать на абсолютную и условную сходимость ряд Решение. Составляем ряд из модулей (Эквивалентность рядов
- 10. 1. Члены ряда убывают по абсолютной величине очевидно, что an > an+1 и первое условие признака
- 11. Задание для самоконтроля Доказать, что сходится условно, но не обладает абсолютной сходимостью.
- 12. Основные свойства абсолютно сходящихся рядов: 1. Если ряд сходится абсолютно и имеет сумму S, то ряд,
- 13. Пример 5. Ряд сходится условно (по признаку Лейбница). Переставляя члены условно сходящегося ряда, можно добиться того,
- 14. Теорема 3 (Римана). В результате перестановки членов условно сходящегося ряда можно получить сходящийся ряд с заранее
- 15. Рассмотрим ряд с комплексными членами Комплексный ряд сходится тогда и только тогда, когда сходятся ряды из
- 16. Пример 6. Исследовать сходимость ряда Решение. Преобразуем общий член ряда Ряд из действительных частей сходится (эквивалентен
- 17. Пример 7. Исследовать сходимость ряда Решение. Преобразуем общий член ряда Ряд из действительных частей знакочередующийся ряд,
- 18. Значит, данный комплексный ряд расходится. Замечание. Тот же результат можно получить быстрее, если начать исследование с
- 19. §4. Функциональные ряды. Равномерная сходимость функционального ряда Ряд, членами которого являются функции, называется функциональным рядом: Придавая
- 20. Если полученный числовой ряд сходится, то точка х0 называется точкой сходимости ряда; если ряд расходится, то
- 21. Пример 1. Найти область сходимости ряда Решение. Преобразуем данный ряд и найдем область сходимости для каждого
- 22. 2. Для определения области сходимости используем признак Даламбера. Ряд сходится, если При ряд расходится. В точках
- 23. Если x =1/2, то получим гармонический ряд, который расходится. Если x =−1/2, то получим условно сходящийся
- 24. Пусть дан функциональный ряд который сходится на некотором множестве Х, тогда его сумма для каждого х∈Х.
- 25. В другой точке х = х2 (х2 ∈ Х), по той же погрешности ε приближение S(х2)
- 26. Сходящийся на множестве Х функциональный ряд называется равномерно сходящимся на множестве Х, если ∀ε > 0
- 27. Критерий Коши (для равномерной сходимости функционального ряда) Пусть сходится к S(x) на множестве Х. Тогда функциональный
- 28. Теорема (признак Вейерштрасса) Если для х∈Х , существует числовой ряд такой, что 1) ∀n: an>0; 2)
- 29. Пример 2. Доказать равномерную сходимость ряда Решение. Воспользуемся признаком Вейерштрасса и подберем мажоранту. Т.к. то ∀n∈N
- 31. Скачать презентацию




























 группа
группа Координатная плоскость
Координатная плоскость Теория вероятностей. Успех и неудача. Число успехов в испытаниях Бернулли
Теория вероятностей. Успех и неудача. Число успехов в испытаниях Бернулли Решение задач на части. 5 класс
Решение задач на части. 5 класс Вычитание вида 17-[], 18-[]
Вычитание вида 17-[], 18-[] Понятие средней величины. Виды средних величин
Понятие средней величины. Виды средних величин Закрепление счёта в пределах 10.
Закрепление счёта в пределах 10. Вычитание чисел
Вычитание чисел Сложение и вычитание одночленов
Сложение и вычитание одночленов Действия с многозначными числами (устные вычисления).
Действия с многозначными числами (устные вычисления). Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка
Представление данных (таблицы, диаграммы, графики), генеральная совокупность, выборка Признаки параллельных прямых. 7 класс
Признаки параллельных прямых. 7 класс Мерительный инструмент
Мерительный инструмент Порядок действий в выражениях со скобками
Порядок действий в выражениях со скобками Нахождение процентов от числа и числа по его проценту
Нахождение процентов от числа и числа по его проценту Смешанные дроби
Смешанные дроби Из истории дроби. Современное обозначение дробей
Из истории дроби. Современное обозначение дробей Графический способ решения системы уравнений с двумя переменными
Графический способ решения системы уравнений с двумя переменными Игра Математик - бизнесмен. 10-11 классы
Игра Математик - бизнесмен. 10-11 классы Кут та його величина. Види кутів (5 клас)
Кут та його величина. Види кутів (5 клас) Формирование основных компетенций на уроках математики
Формирование основных компетенций на уроках математики Chapter 1. Polynomial and Rational Functions. 3.3. Dividing Polynomials; Remainder and Factor Theorems
Chapter 1. Polynomial and Rational Functions. 3.3. Dividing Polynomials; Remainder and Factor Theorems Подобные треугольники (8 класс)
Подобные треугольники (8 класс) Весёлые числа (часть 2)
Весёлые числа (часть 2) С Бибигоном на Луну
С Бибигоном на Луну Математика – білім негізі
Математика – білім негізі Урок математики Числа от 1 до 10. Закрепление
Урок математики Числа от 1 до 10. Закрепление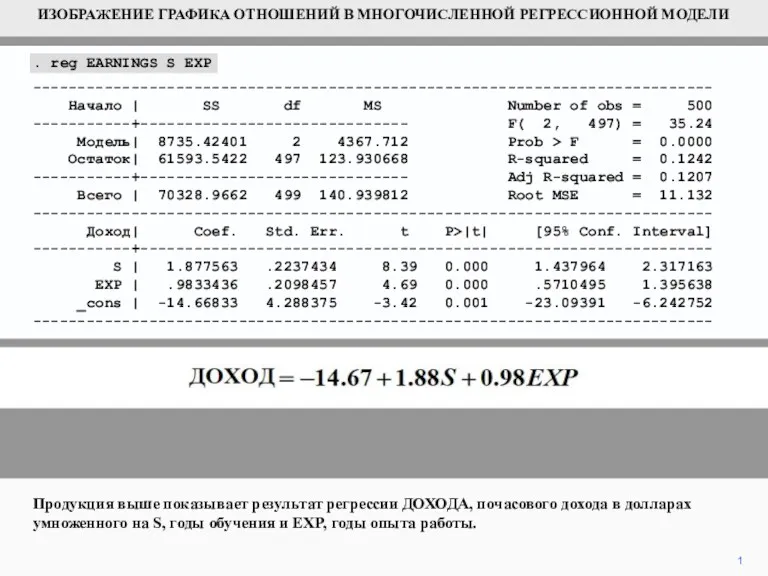 Изображение графика отношений в многочисленной регрессионной модели
Изображение графика отношений в многочисленной регрессионной модели