Содержание
- 2. Плаксина Юлия Геннадьевна Доцент кафедры электронных вычислительных машин 8(3466)-267-90-50 plaksinayg@yandex.ru ЮУрГУ, 811/3б корпус
- 3. Дискретная математика – область математики, занимающаяся изучение дискретных структур (т.е. структур конечного характера), которые возникают как
- 4. Дискретные структуры конечные графы; конечные автоматы; машины Тьюринга и Поста; некоторые модели преобразователей информации. Это структуры
- 5. Дискретная математика также изучает некоторые алгебраические системы: - группы; - кольца; - поля; - частично упорядоченные
- 6. Разделы дискретной математики: Математическая логика. Математическая кибернетика. Теория функциональных систем. Общая алгебра. Комбинаторика. Теория графов. Машинная
- 7. Разделы дискретной математики: 12. Теория конечных автоматов. 13. Теория множеств. 14. Теория формальных грамматик. 15. Теория
- 8. В дискретной математике нет понятия - бесконечного множества, - предельного перехода, - непрерывности, - дифференцируемости.
- 9. Любое понятие дискретной математики можно определить с помощью понятия множества.
- 10. Основателем теории множеств является Георг Кантор немецкий математик (3.3.1845, Петербург, - 6.1.1918, Галле)
- 11. Определение Г. Кантором понятия «множество» Под «множеством» мы понимаем соединение в некое целое M определённых хорошо
- 12. Определения понятия «множество» Под множеством понимается некоторая, вполне определенная совокупность объектов или элементов. Множество – совокупность
- 13. Таким образом: Множество – любая совокупность объектов, которая обладает следую-щими свойствами: Элементы множества представляют собой попарно
- 14. Объекты, составляющие множество, называются элементами множества и обозначаются маленькими латинскими буквами (например, x, a, b, bi,
- 15. Множества обычно обозначаются заглавными латинскими буквами (например, A, B, C, D)
- 16. Для некоторых множеств приняты специальные обозначения: N – множество натуральных чисел; {1,2,3,…,100,101,…} Z – множество целых
- 17. Q – множество рациональных чисел. Целые и дробные числа (обыкновенные дроби, конечные десятичные дроби и бесконечные
- 18. Число «ПИ» ( п=3.ю14…), основание натурального логарифма e (e = 2,718…) или не являются рациональными числами.
- 20. Любое рациональное число можно представить в виде дроби, у которой числитель принадлежит целым числам, а знаменатель
- 22. R – множество действительных чисел;
- 23. Для некоторых множеств приняты специальные обозначения: C – множество комплексных чисел. Комплексное число – это выражение
- 24. Мнимая единица – символ, квадрат которого равен -1, т.е
- 25. Число а – действительная часть, b – мнимая часть комплексного числа ! Действительные числа – частный
- 26. Пример {1,2.3,4} – множество, содержащее натуральные числа 1,2,3 и 4.
- 27. а А (а принадлежит А) а А (а не принадлежит А)
- 28. Пример 3 {1,2,3,4} 5 {1,2,3,4}
- 29. - «тогда и только тогда, когда»; - «существует х такой, что»; - «для всякого х»; -
- 30. Понятие конечного множества Множество называется конечным, если оно состоит из конечного числа элементов.
- 31. Пример Элементы конечного множества А можно обозначить через a1, a2, …, a5: А = {a1, a2,
- 32. Пример Бесконечными являются множества всех натуральных (N), целых (Z), действительных (R) чисел.
- 33. Понятие «счетного множества» Счетное множество – это множество А, все элементы которого могут быть занумерованы в
- 34. Например. Дано множество , тогда . Различия между отношениями принадлежности и включения: если , то ,
- 35. Понятие «мощность множества» Мощностью множества А называется количество входящих в его состав различных элементов и обозначается
- 36. Пример A = {a, b, c, d} |A|=4 B = {a, b, {a, b}, a} |B|=3
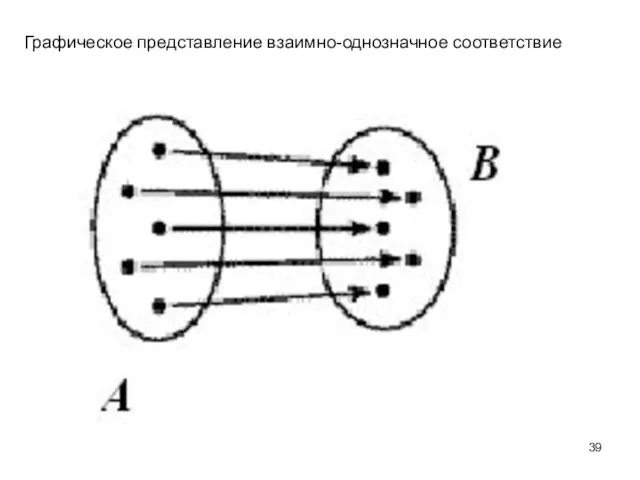
- 37. Понятие равномощного множества Множества А и В называются равномощными, если между их элементами существует взаимно-однозначное соответствие.
- 38. Взаимно-однозначное соответствие предполагает, что каждому элементу множества B поставлен в соответствие ровно один элемент множества A.
- 39. Графическое представление взаимно-однозначное соответствие
- 40. Пример Множества {0, 1, 2} и {лошадь, корова, телевизор} - равномощны, Множества {0, 1, 2} и
- 41. Пример Множество N и множество четных чисел также равномощны: N: 1 2 3 4 5 6
- 42. Два множества равны, тогда и только тогда, когда они состоят из одних и тех же элементов.
- 43. Примеры Множества А = {2,4,6} и В = {2,6,4} равны. Так как состоят из одних и
- 44. Способы задания множеств
- 45. Способы задания множеств 1.Табличная форма или перечисление элементов. А = { a1, a2, …, an }
- 46. Пример множество студентов данной группы определяется их списком в журнале; множество всех стран на земном шаре
- 47. Способы задания множеств 2. Описание признака или свойства элементов множества. Множество = {х | х обладает
- 48. Понятие свойства Под свойством предмета Х будем понимать такое повествовательное предложение, в котором нечто утверждается относительно
- 49. Пример 1. Свойство «быть квадратом целого числа» задает (бесконечное) множество всех квадратов целых чисел: A =
- 50. Способы задания множеств 3. С помощью порождающей процедуры. Каждый последующий элемент множества определяется на основании предшествующих
- 51. Примеры 1. Каждый последующий элемент есть сумма двух предыдущих, задается следующим образом: D = {xk |
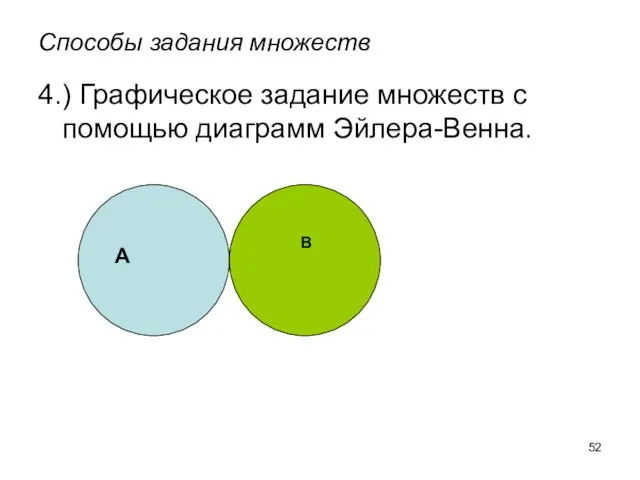
- 52. Способы задания множеств 4.) Графическое задание множеств с помощью диаграмм Эйлера-Венна. А В
- 53. Таким образом, 1. Способ задания множества должен быть адекватным, т.е. полностью определять множество. Это возможно, если
- 54. Понятие «пустое множество» Пустое множество - множество, не содержащее ни одного элемента. Оно обозначается Ø и
- 55. Множества {Ø} и {{Ø}} неравномощные. В множестве {Ø} нет ни одного элемента, а в множестве {{Ø}}
- 56. Понятие универсального множества Универсальное множество U: есть множество, обладающее таким свойством, что все рассматриваемые множества являются
- 57. В теории чисел универсальное множество обычно совпадает со множеством всех целых или натуральных чисел. В математическом
- 58. Теоретико-множественные отношения
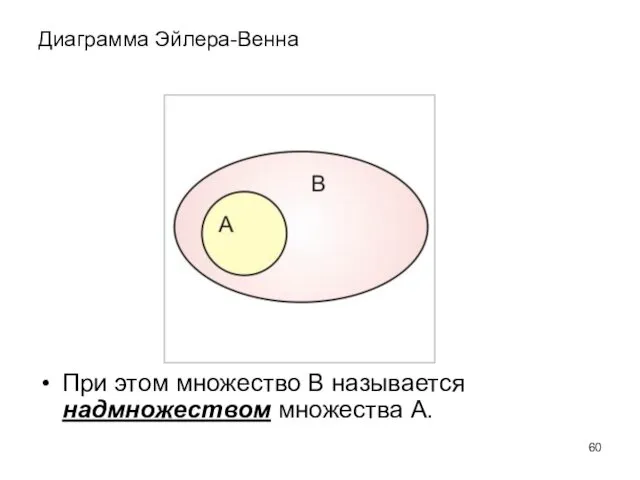
- 59. Отношение нестрогого включения Множество А называют подмножеством множества В, если каждый элемент множества А является также
- 60. Диаграмма Эйлера-Венна При этом множество В называется надмножеством множества А.
- 61. Пример Множество всех четных чисел является подмножеством множества всех целых чисел, множество {0, 1, 2} –
- 62. Если А не является подмножеством В это записывается как А В Пример: {1,2,3} {1,2,3,4}, {1,2,5,} {1,2,3,4},
- 63. Каждое множество есть подмножество универсального множества U. Пустое множество есть подмножество любого данного множества А, так
- 64. Любое множество является подмножеством самого себя, т.е. для любого множества А справедливо включение
- 65. Два множества называются равными, если каждый элемент любого из них необходимо является элементом другого. А =
- 67. Отношение строгого включения Подмножество А строго включается во множество В , если оно нестрого включается во
- 68. В этом случае А называется собственным подмножеством или собственной частью множества В.
- 69. Любое множество, отличное от несобственного, называется собственным подмножеством данного множества.
- 70. Пример Множество А = {а, b, c} является собственным подмножеством множества В = {а, b, c,
- 71. Верна цепочка включений числовых множеств: множество натуральных чисел N является подмножеством множества целых чисел Z, которое
- 72. Выводы: 1. Пустое множество является подмножеством любого множества. 2. Любое множество является подмножеством самого себя. 3.
- 73. Выводы: 4. У пустого множества нет собственных подмножеств. 5. Оба несобственных подмножества равны между собой. 6.
- 74. Если А ={3,5}, то собственными подмножествами множества А будут являться множества {3} и {5}
- 75. Отношение включения и отношение принадлежности
- 76. Если так, тогда операции включения и отношение принадлежности суть одно и то же? Нет. Принадлежность -
- 77. Очень важно не смешивать отношения принадлежностии включения: если {а}М, то аМ, и наоборот; но из {a}М
- 79. Понятие булеана множества Количество всех подмножеств (множество всех подмножеств) некоторого множества А называется его булеаном, или
- 80. Пример А = {1, 3, 5}, Р(А) = {Ø, {1}, {3}, {5}, {1,3}, {1,5}, {3,5}, {1,3,5}}.
- 81. Пример Пусть A = { 1,2,3,4,...,n }, |A | = n. Найдем мощность множества Р(A).
- 82. Для определения Р(A) воспользуемся биномиальными коэффициентами (число сочетаний из n по k)
- 83. Перечислим по порядку, начиная с пустого множества, все подмножества множества A: пустому подмножеству множества A поставим
- 84. Булеан содержит следующие двухэлементные подмножества: { 1,2 },{ 1,3 },{ 1,4 },… ,{ 1,n },{ 2,3
- 85. Булеан содержит: - трехэлементных подмножеств, четырехэлементных подмножеств
- 86. (n - 1)-элементных подмножеств и одно n элементное подмножество (само множество A), которому сопоставляется биномиальный коэффициент
- 87. Сумма всех биномиальных коэффициентов покажет количество элементов булеана Р(A) 2n =(1 + 1)n = P (A)=2n
- 88. Количество собственных подмножеств некоторого множества А равно 2 |A| -1.
- 89. Теорема. Каково бы ни было множество A, множество его подмножеств P(A) неравномощно самому множеству A.
- 90. Свойства теоретико-множественных отношений
- 91. Свойства теоретико-множественных отношений
- 93. Скачать презентацию

















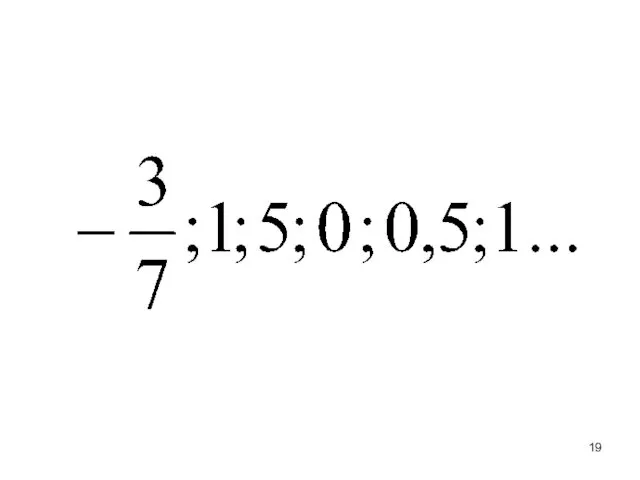

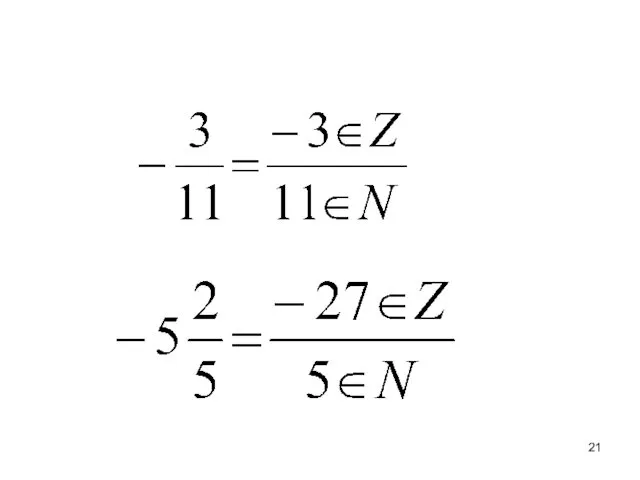



































































 Элементы комбинаторики и теории вероятностей
Элементы комбинаторики и теории вероятностей Табличное умножение и деление. 2 класс
Табличное умножение и деление. 2 класс Приёмы письменных вычислений
Приёмы письменных вычислений Что узнали, чему научились. Урок математики 2 класс
Что узнали, чему научились. Урок математики 2 класс Математический калейдоскоп
Математический калейдоскоп Аксиомы стереометрии
Аксиомы стереометрии Решение текстовых задач на все арифметические действия
Решение текстовых задач на все арифметические действия Длина отрезка
Длина отрезка Умножение и деление. Конкретный смысл умножения. 2 класс
Умножение и деление. Конкретный смысл умножения. 2 класс Презентация к уроку математики по теме Признаки предметов 1 класс, программа 2100, урок №5
Презентация к уроку математики по теме Признаки предметов 1 класс, программа 2100, урок №5 Разложение многочлена на множители. урок-путешествие
Разложение многочлена на множители. урок-путешествие Графический метод решения системы уравнений с двумя переменными
Графический метод решения системы уравнений с двумя переменными Функция y=sinx. Свойства. Преобразование графиков
Функция y=sinx. Свойства. Преобразование графиков Задачи на движение по реке
Задачи на движение по реке Цилиндр. Конус. Шар
Цилиндр. Конус. Шар Медианы, биссектрисы и высоты треугольника. Свойства равнобедренного треугольника
Медианы, биссектрисы и высоты треугольника. Свойства равнобедренного треугольника Дециметр
Дециметр Столбчатые диаграммы и графики
Столбчатые диаграммы и графики Повторение знаний о нумерации. Числа от 11 до 20
Повторение знаний о нумерации. Числа от 11 до 20 Урок повторения и обобщения знаний по теме: Площадь
Урок повторения и обобщения знаний по теме: Площадь Презентация для учащихся 2 класса Устный счёт с Дедом Морозом и Снегурочкой
Презентация для учащихся 2 класса Устный счёт с Дедом Морозом и Снегурочкой Относительная частота случайного события. 9 класс
Относительная частота случайного события. 9 класс ОГЭ. Математика. Задания 1-5. Демо-версия
ОГЭ. Математика. Задания 1-5. Демо-версия Конспект НОД по ФЭМП По следам Колобка
Конспект НОД по ФЭМП По следам Колобка тренажер по математике числа первого десятка
тренажер по математике числа первого десятка Умножение и деление чисел (2 класс)
Умножение и деление чисел (2 класс) Решение заданий В10 по материалам открытого банка задач ЕГЭ
Решение заданий В10 по материалам открытого банка задач ЕГЭ Подобные треугольники. Повторение к ОГЭ
Подобные треугольники. Повторение к ОГЭ