Содержание
- 2. Справочные данные Кафедра АИВС (Автоматизированных информационных и вычислительных систем) Преподаватель Мякушко Эдуард Валерьевич Заведующий кафедрой Крушный
- 3. Введение Дискре́тная матема́тика — часть математики, изучающая дискретные математические структуры, такие, как графы и утверждения в
- 4. Введение Дискретная математика – математический аппарат, заложенный в основу работы всех основных цифровых устройств. Студент изучающий
- 5. Информационно - измерительная система Человек Органы чувств Мозг Исполнительные органы
- 6. Информационно - измерительная система Техническая Измерительные устройства(датчики) Цифровая вычислительная машина Исполнительные устройства
- 7. Восприятие внешнего мира информационно – измерительными системами Объекты который присутствуют вокруг нас (внешний мир), будем воспринимать
- 8. Мое личное определение, что есть множество. Множество – это совокупность различных объектов, объединенное в единое целое.
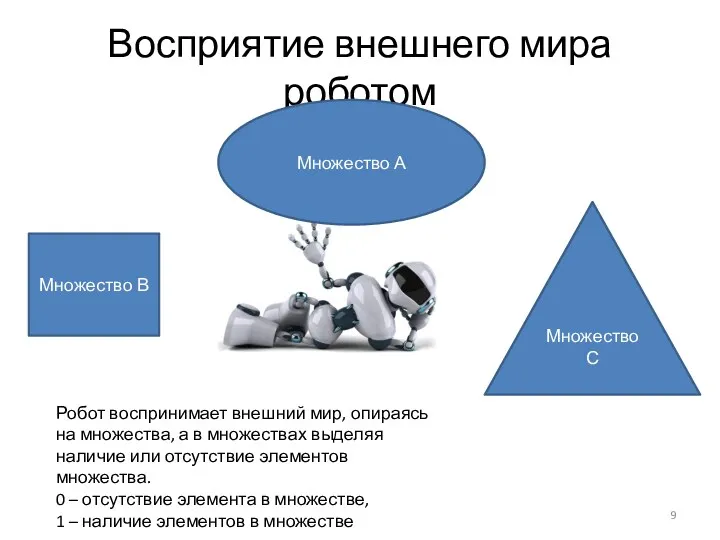
- 9. Восприятие внешнего мира роботом Множество А Множество В Множество С Робот воспринимает внешний мир, опираясь на
- 10. 00011110010101010100010101001010101010101001010101010101010101010101 00011110010101010100010101001010101010101001010101010101010101010 00011110010101010100010101001010101010101001010101010101010101010 00011110010101010100010101001010101010101001010101010101010101010 00011110010101010100010101001010101010101001010101010101010101010 00011110010101010100010101001010101010101001010101010101010101010 00011110010101010100010101001010101010101001010101010101010101010
- 11. Формальное представление множеств А = {a, b, c, d} a ∈ A, b ∈ A, c
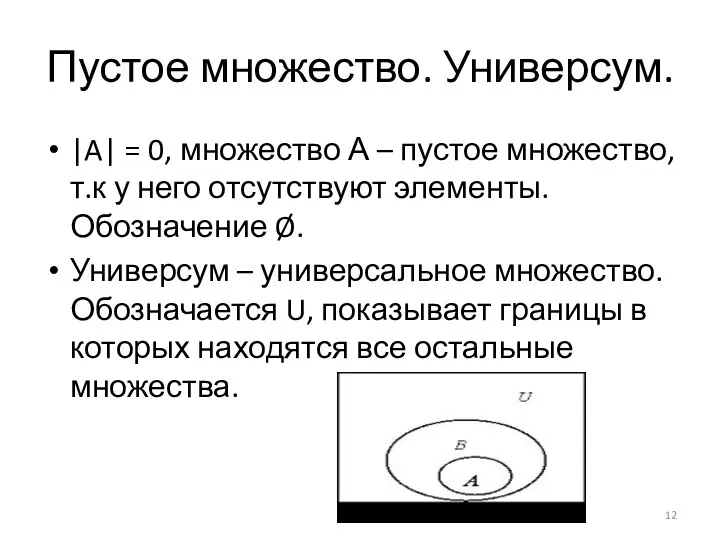
- 12. Пустое множество. Универсум. |A| = 0, множество А – пустое множество, т.к у него отсутствуют элементы.
- 13. Множество. Вектор. A= {a,b,c,d},элементы множества можно перемещать. Важно наличие элемента, а не его положение. A =
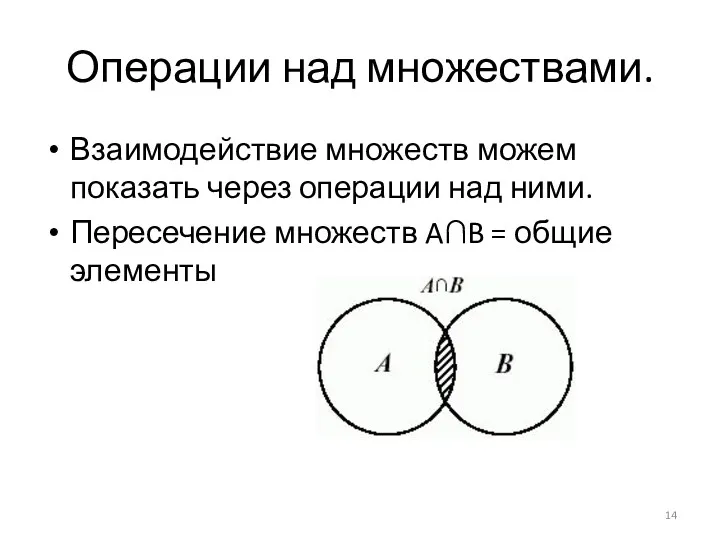
- 14. Операции над множествами. Взаимодействие множеств можем показать через операции над ними. Пересечение множеств A∩B = общие
- 15. Пример пересечения множеств. |U| = 10, |A| = 8, |B| = 5, |A ∩ B| =
- 16. Объединение множеств. |U| = 10, |A| = 8, |B| = 5 |A ᴜ B| = 10
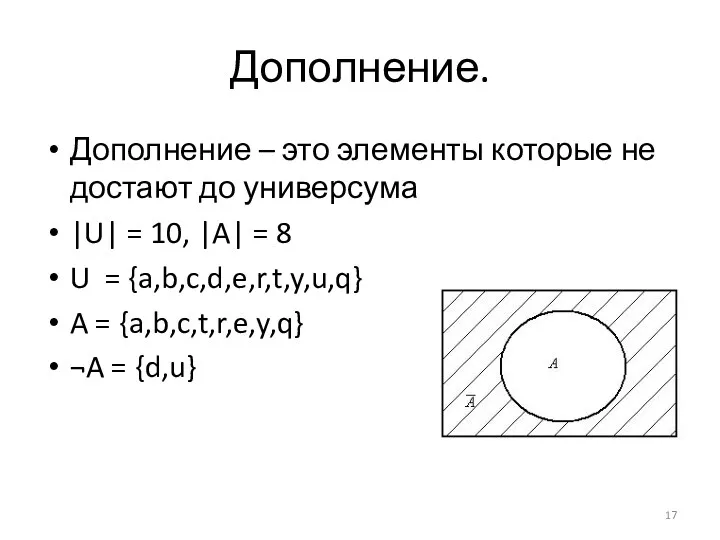
- 17. Дополнение. Дополнение – это элементы которые не достают до универсума |U| = 10, |A| = 8
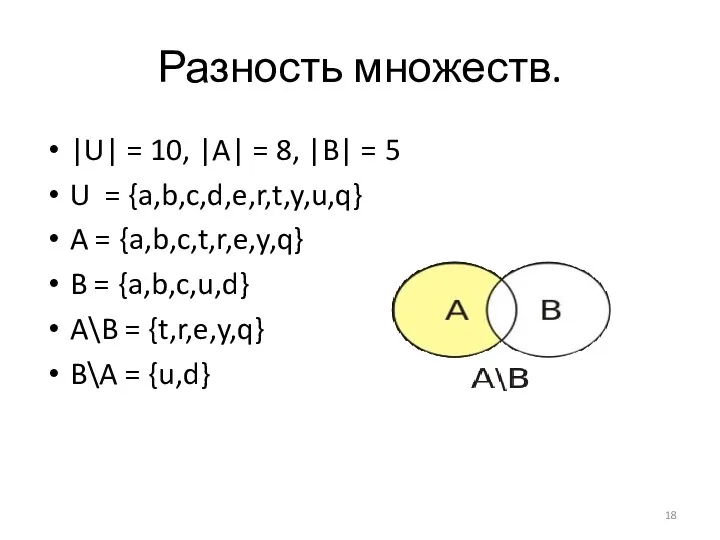
- 18. Разность множеств. |U| = 10, |A| = 8, |B| = 5 U = {a,b,c,d,e,r,t,y,u,q} A =
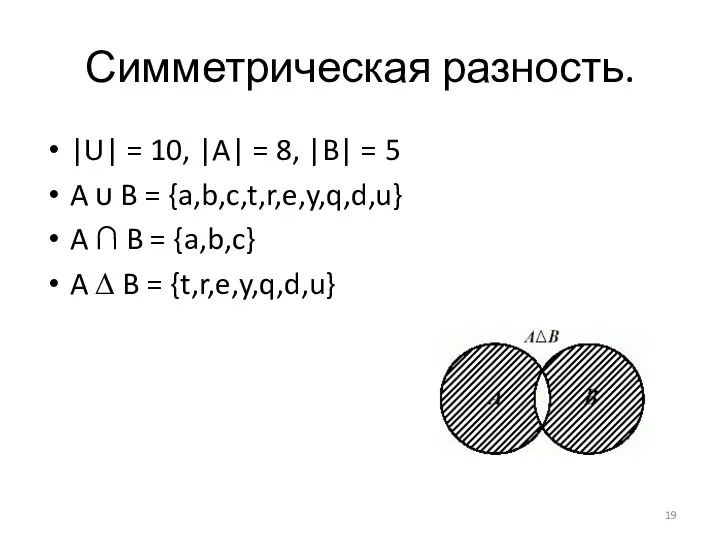
- 19. Симметрическая разность. |U| = 10, |A| = 8, |B| = 5 A ᴜ B = {a,b,c,t,r,e,y,q,d,u}
- 20. Самостоятельная работа.
- 21. Множество подмножеств.(Булеан) A = {x,y,z} β(A) – множество подмножеств β(A) = {Ø,{x},{y},{z},{xy},{xz},{yz},{x,y,z}} | β(A) | =
- 22. Взаимно – однозначные соответствия Булеана и множества двоичных векторов β(A) = Ø↔(0,0,0) {x} ↔(1,0,0) {y} ↔(0,1,0)
- 23. Пример A = {a,b,c,d} β(A) = Ø↔(0,0,0,0,) {a,b,c,d} ↔(1,1,1,1) {a,b} ↔(1,1,0,0) {a,c} ↔(1,0,1,0) {a,d} ↔(1,0,0,1) {b,c}
- 24. Взаимодействие объектов показывается через операции над подмножествами β(A) = Ø↔(0,0,0) {x} ↔(1,0,0) {y} ↔(0,1,0) {z} ↔(0,0,1)
- 25. Пример №2 A = {a,b,c,d} β(A) = Ø↔(0,0,0,0) {a,b,c,d} ↔(1,1,1,1) {a,b}∩{c,d} = Ø↔(1,1,0,0)*(0,0,1,1)=(0,0,0,0) {a,c}U{b,d} = {a,b,c,d}
- 26. Опреации над множествами(подмножествами) обладают определенными свойствами
- 27. Взаимно – однозначные соответствия для построения цифровых технических систем (β(A), U, ∩, -) ↕ ↕ ↕
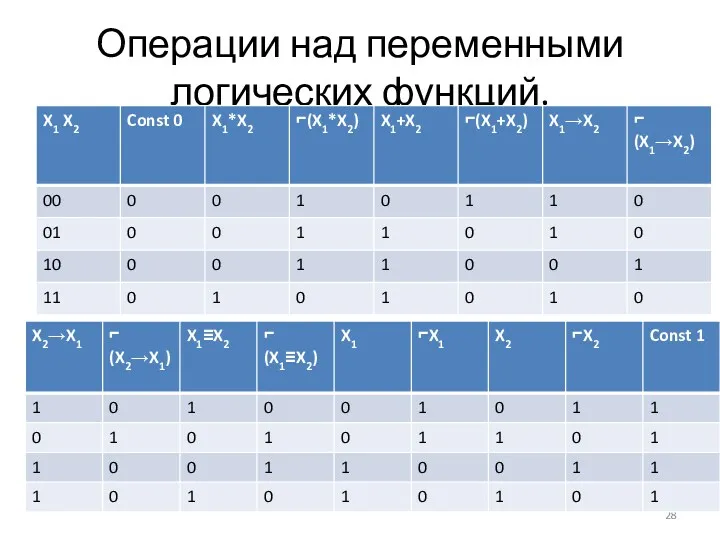
- 28. Операции над переменными логических функций.
- 29. Отношения 1 2 a b c d e f j h z x y o p
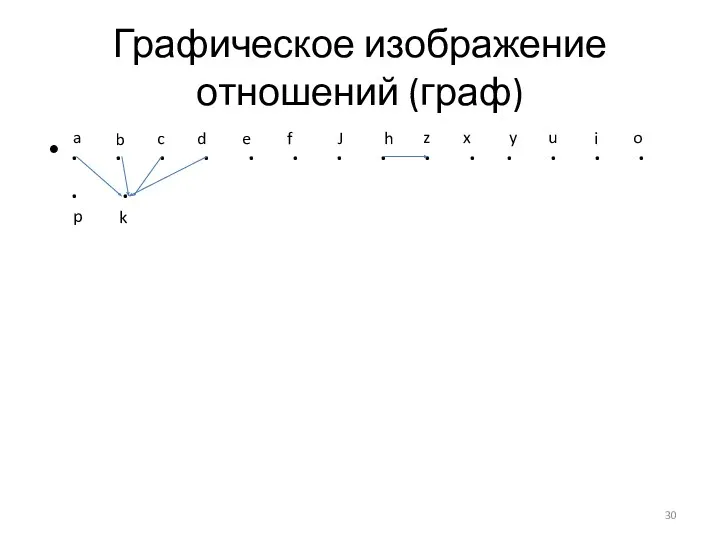
- 30. Графическое изображение отношений (граф) . . . . . . . . . . . .
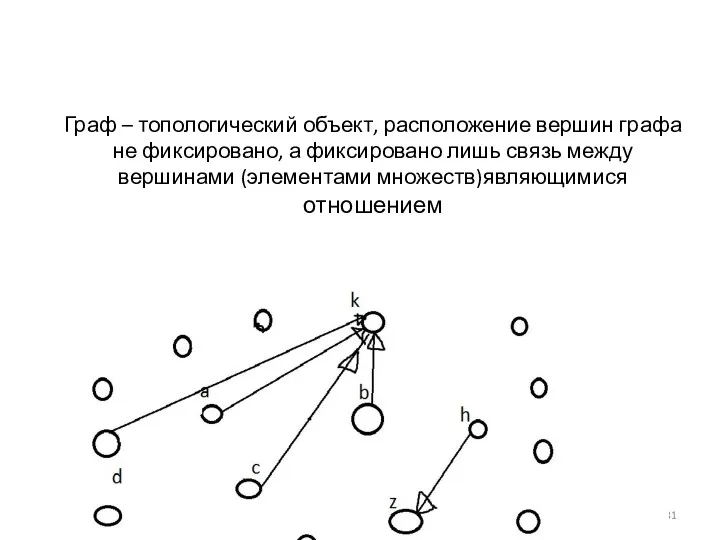
- 31. Граф – топологический объект, расположение вершин графа не фиксировано, а фиксировано лишь связь между вершинами (элементами
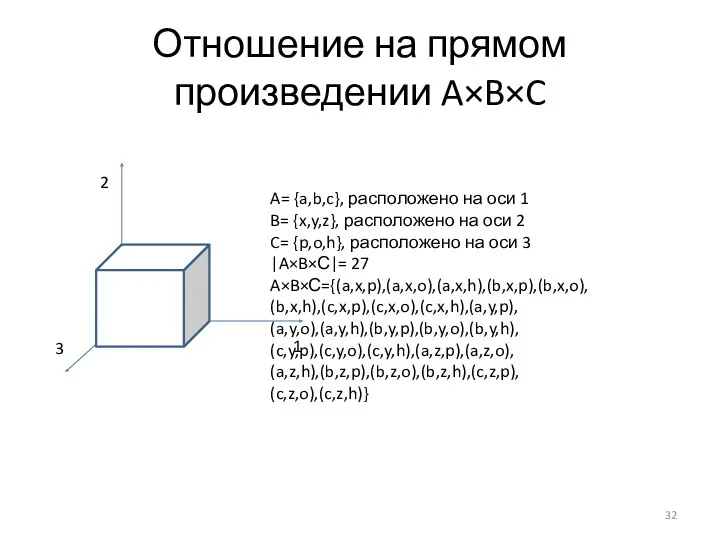
- 32. Отношение на прямом произведении A×B×C 1 2 3 A= {a,b,c}, расположено на оси 1 B= {x,y,z},
- 33. Примеры отношения на прямом произведении A×B×C R⊆A×B×C |R|=8, R ={(a,x,p),(a,x,o),(a,x,h),(b,x,p),(b,x,o), (b,x,h),(c,x,p),(c,x,o)}
- 34. Операции над отношениями R1⊆A×B, |A| = 5, |B| = 5, A ={a,b,c,d,e}, B = {f,i,j,h,k} R2
- 35. Обратное отношение. R-1 – обозначение обратного отношения. R = {(a,b),(c,d),(e,f),(i,j)} R-1 = {(b,a),(d,c),(f,e),(j,i)} Т.о отношение осуществляется
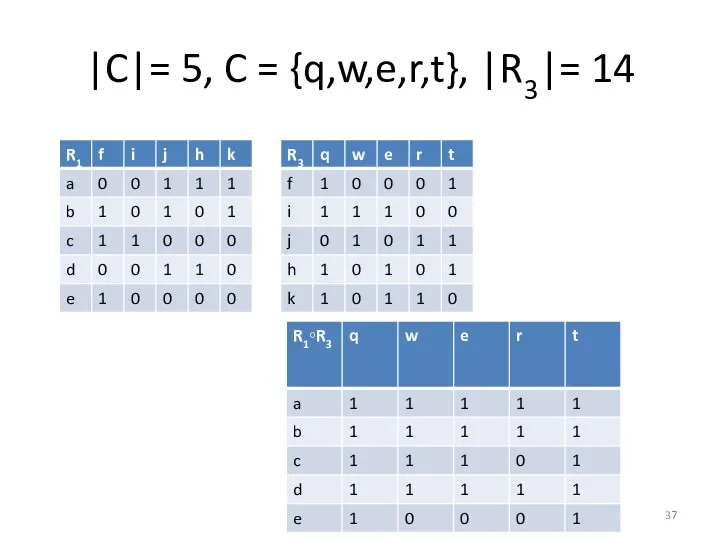
- 36. Композиция отношений. R1⊆A×B R3⊆B×C R1⊆A×B R1 ◦ R3 - обозначение операции. R1 ◦ R3⊆A×С, таким образом
- 37. |C|= 5, C = {q,w,e,r,t}, |R3|= 14
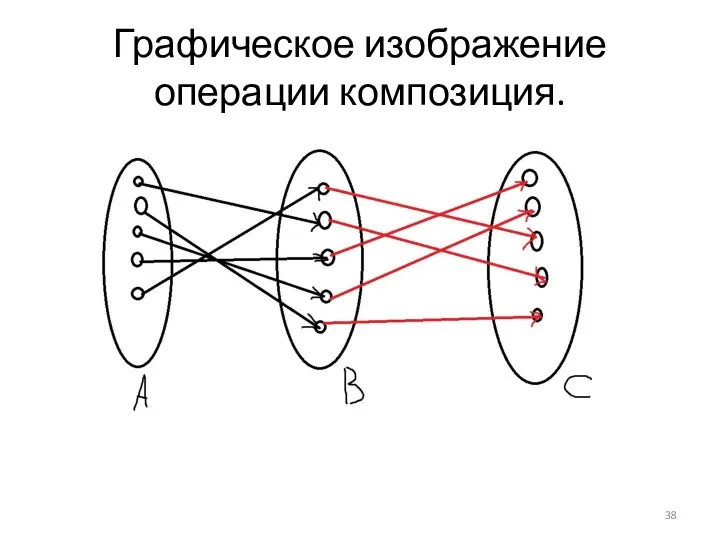
- 38. Графическое изображение операции композиция.
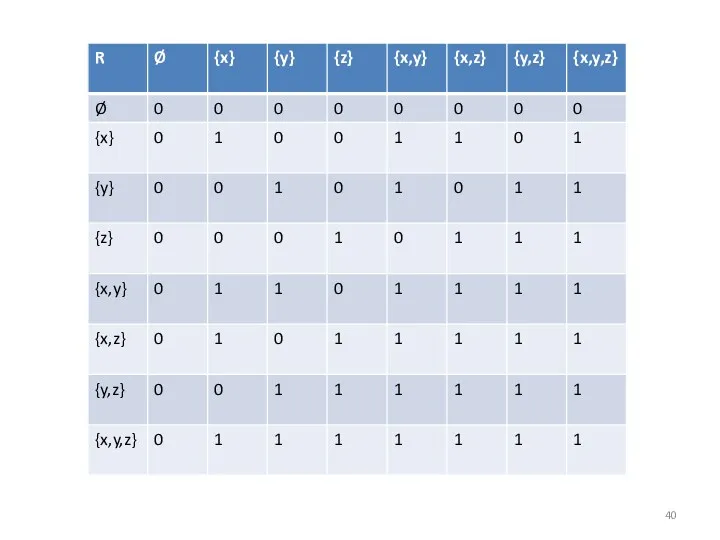
- 39. Отношения на прямом произведении Булеана. R⊆β(A) × β(A), где А = {x,y,z}, R - пересечение
- 41. Контрольная работа №2 R1⊆A×B R2⊆A×B R3⊆B×C |A|=|B|=|C|=10;| R1 | = 70, | R2| = 80 |
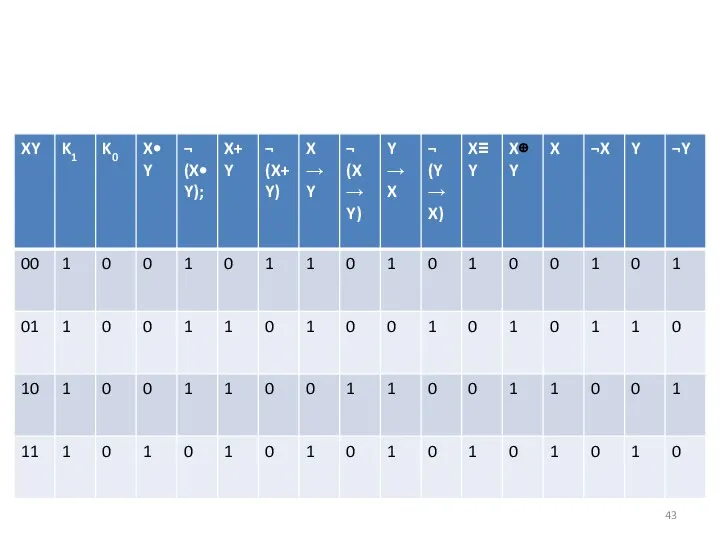
- 42. Переменные логических функций. Операции над переменными логических функций.
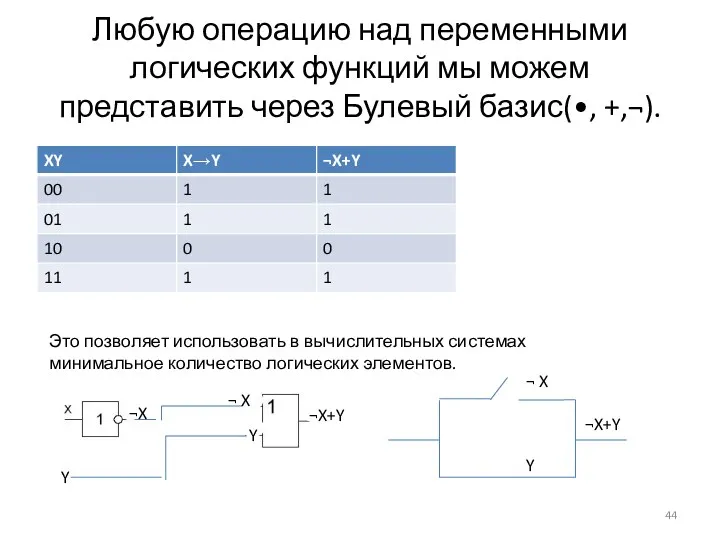
- 44. Любую операцию над переменными логических функций мы можем представить через Булевый базис(•, +,¬). Это позволяет использовать
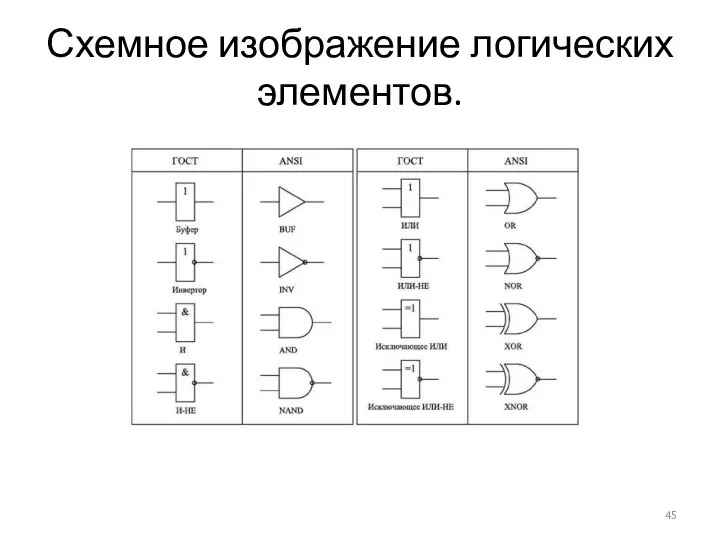
- 45. Схемное изображение логических элементов.
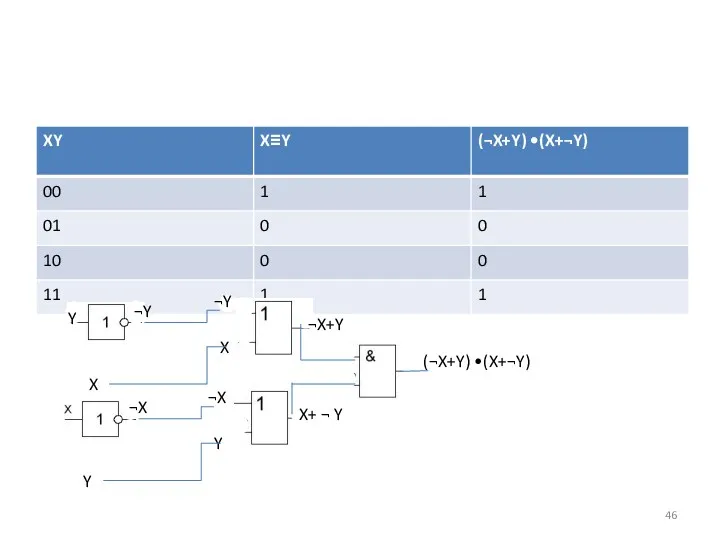
- 46. ¬X ¬X Y Y ¬Y ¬Y X X Y ¬X+Y X+ ¬ Y (¬X+Y) •(X+¬Y)
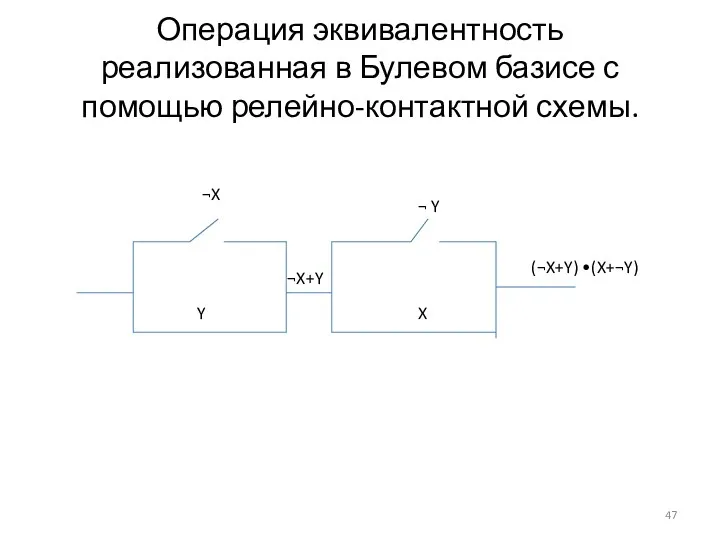
- 47. Операция эквивалентность реализованная в Булевом базисе с помощью релейно-контактной схемы. ¬X Y ¬X+Y ¬ Y X
- 48. Таблица истинности(переключательная таблица) С помощью таблиц истинности получаем результат логической функции для любого числа переменных. Пример:
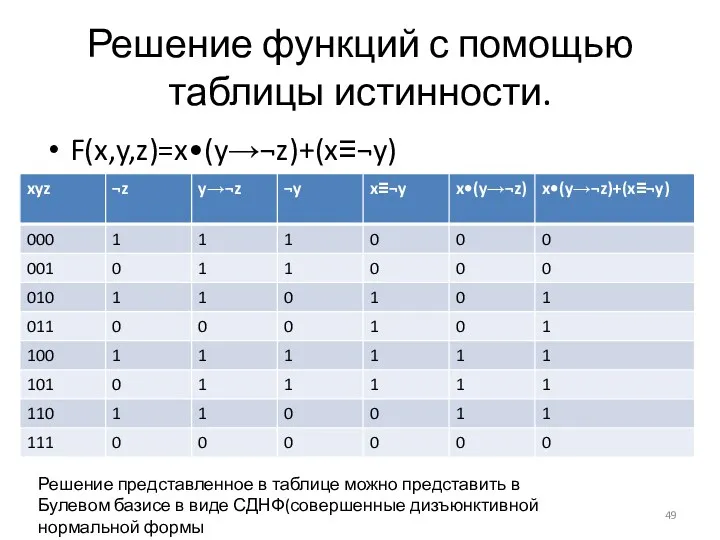
- 49. Решение функций с помощью таблицы истинности. F(x,y,z)=x•(y→¬z)+(x≡¬y) Решение представленное в таблице можно представить в Булевом базисе
- 50. Решение функций с помощью таблицы истинности. F(x,y,z)=x•(y→¬z)+(x≡¬y) СДНФ включает в себя те наборы переменных на которых
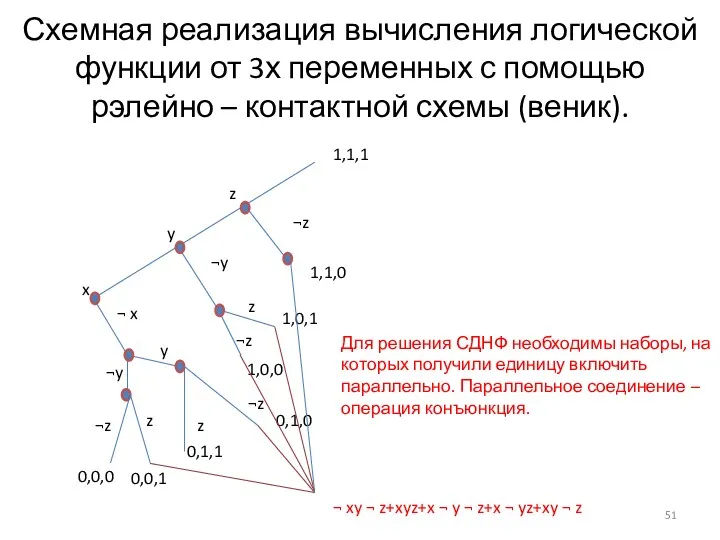
- 51. Схемная реализация вычисления логической функции от 3х переменных с помощью рэлейно – контактной схемы (веник). ¬
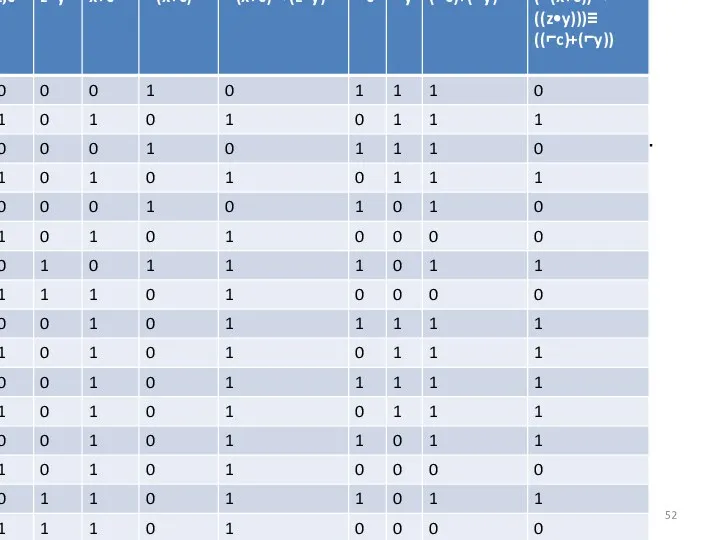
- 52. Минимизация СДНФ с использованием карты Карно. Имеем логическую функцию F(x,y,z,c)=(⌐(x+c))→((z•y)))≡((⌐c)+(⌐y))
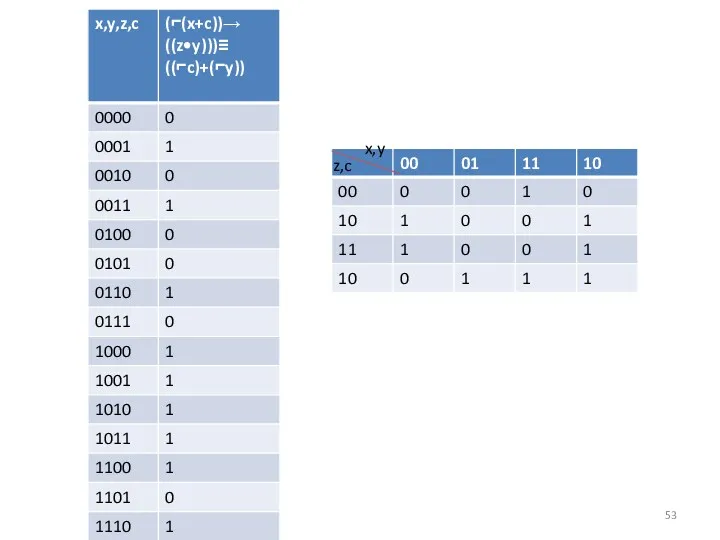
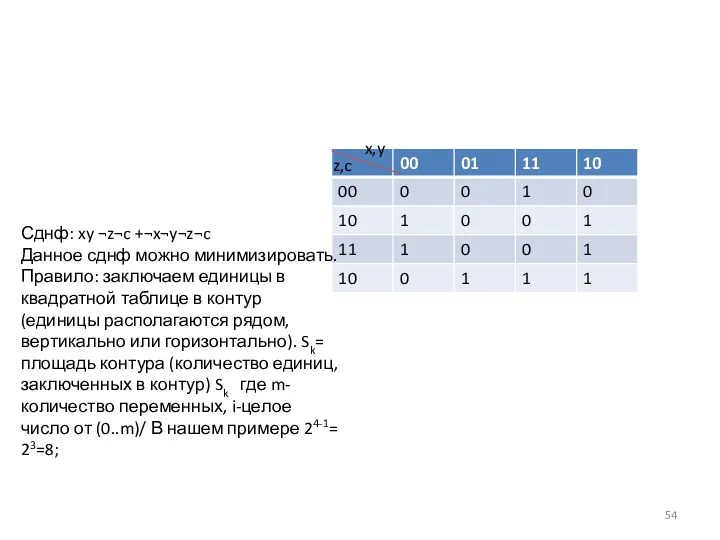
- 53. x,y z,c
- 54. x,y z,c Сднф: xy ¬z¬c +¬x¬y¬z¬c Данное сднф можно минимизировать. Правило: заключаем единицы в квадратной таблице
- 55. x,y z,c В зеленый контур входят:¬xy¬z¬c + ¬x¬y¬z¬c количество сохраняемых переменных в контуре n=log2Sk=1 ¬xy¬z¬c +
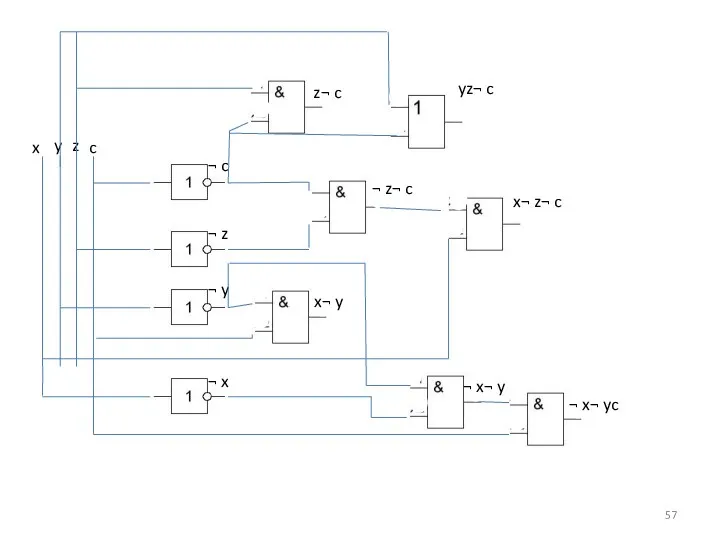
- 56. СДНФ: xy¬z¬c ᴜ x¬y¬z¬c ᴜ ¬x¬y¬zc ᴜ x¬y¬zc ᴜ ¬x¬yzc ᴜ x¬yzc ᴜ ¬xyz¬c ᴜ xyz¬c
- 57. x y z c ¬ c ¬ z ¬ y ¬ z¬ c x¬ z¬ c
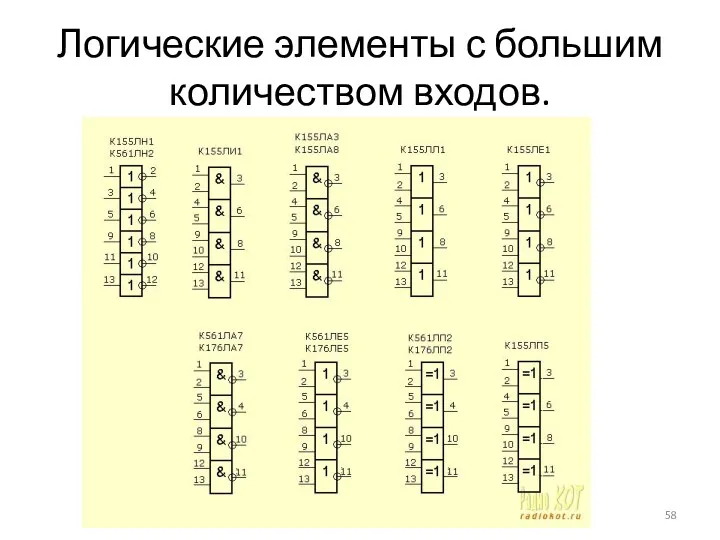
- 58. Логические элементы с большим количеством входов.
- 59. Графы. Граф состоит из множества вершин и множества ребер (ребра соединяют вершины или одну вершину). Если
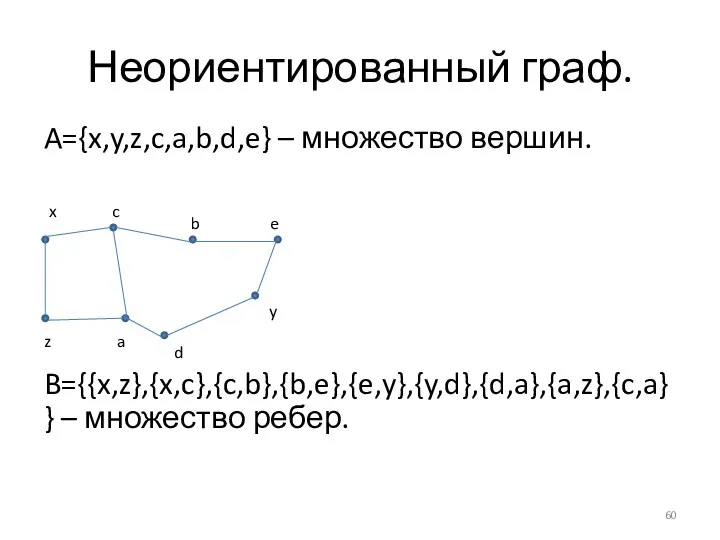
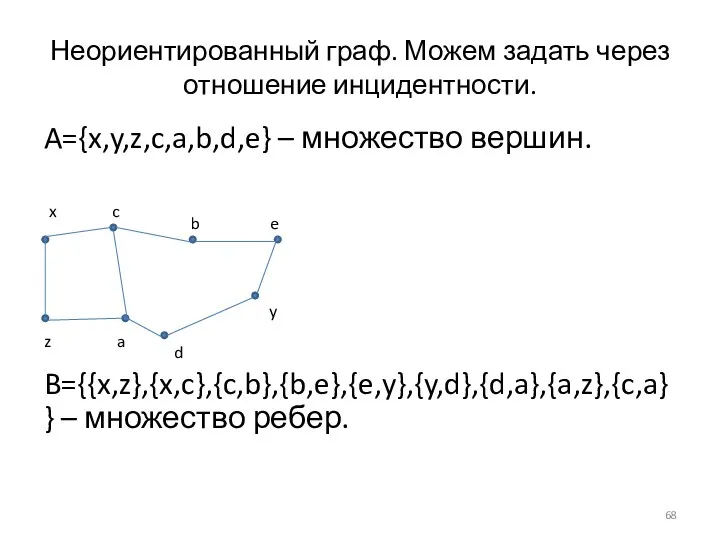
- 60. Неориентированный граф. A={x,y,z,c,a,b,d,e} – множество вершин. B={{x,z},{x,c},{c,b},{b,e},{e,y},{y,d},{d,a},{a,z},{c,a}} – множество ребер.
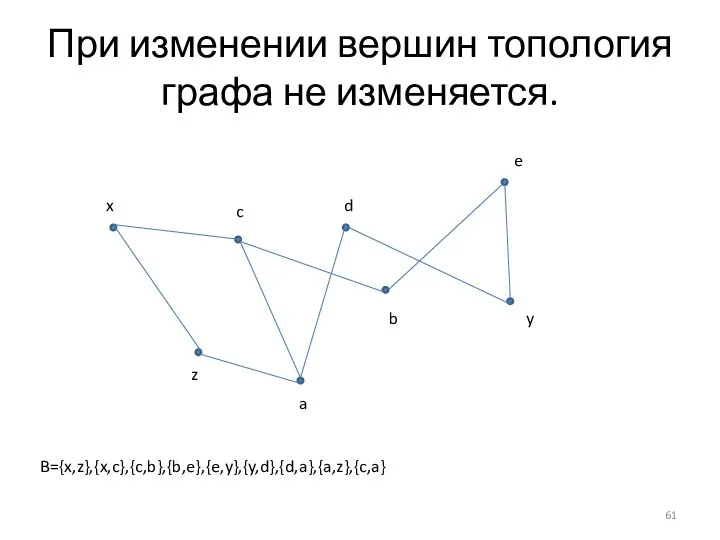
- 61. При изменении вершин топология графа не изменяется. x c z d a b e y B={x,z},{x,c},{c,b},{b,e},{e,y},{y,d},{d,a},{a,z},{c,a}
- 62. Задание графа с помощью отношения смежности. Отношение смежности отношение между вершинами графа. Если вершины графа соединены
- 63. Зададим неориентированный граф через отношение смежности. B={{x,z},{x,c},{c,b},{b,e},{e,y},{y,d},{d,a},{a,z},{c,a}} – множество ребер. Если в главной диагонали будут одни
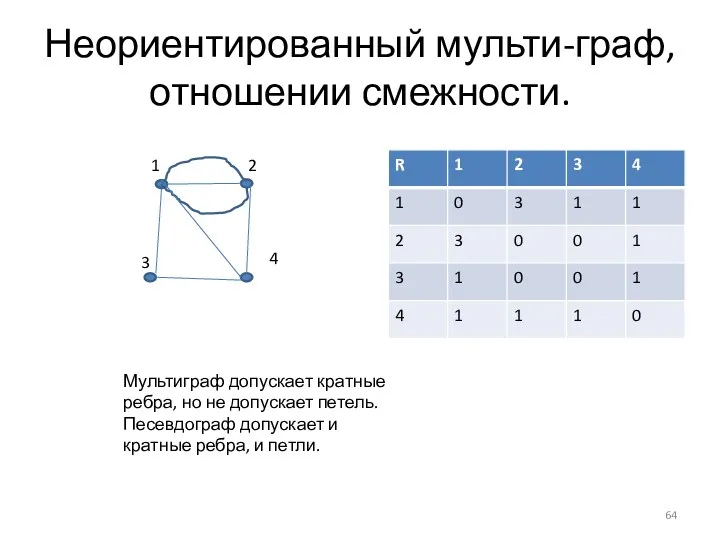
- 64. Неориентированный мульти-граф, отношении смежности. 1 2 3 4 Мультиграф допускает кратные ребра, но не допускает петель.
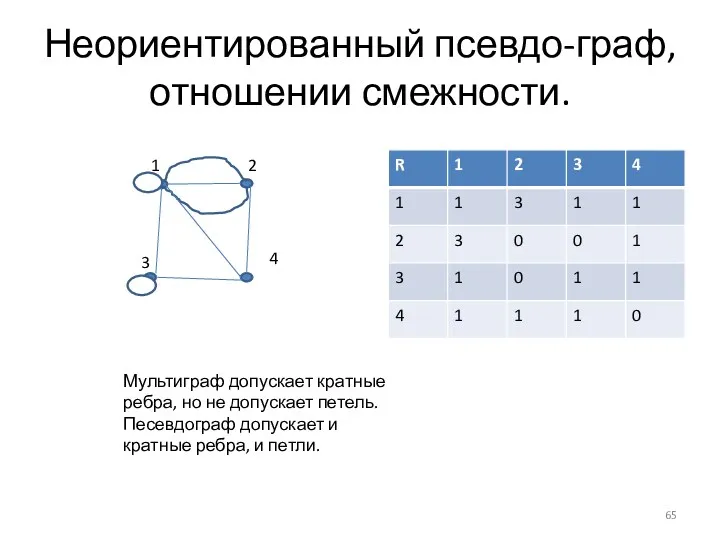
- 65. Неориентированный псевдо-граф, отношении смежности. 1 2 3 4 Мультиграф допускает кратные ребра, но не допускает петель.
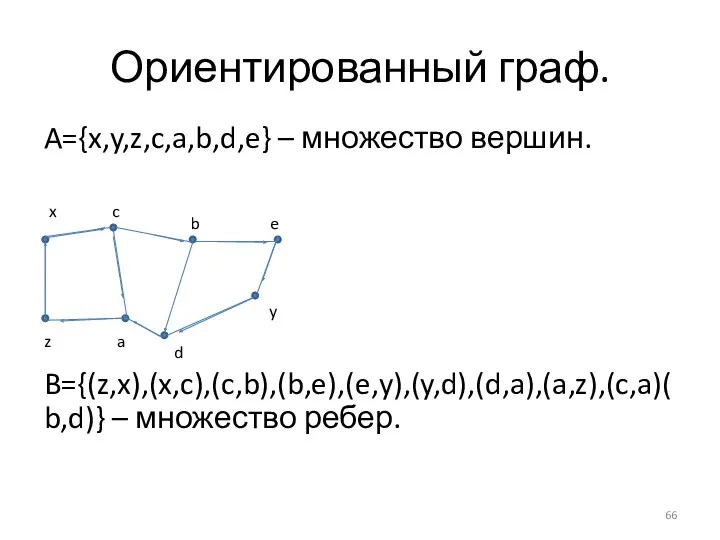
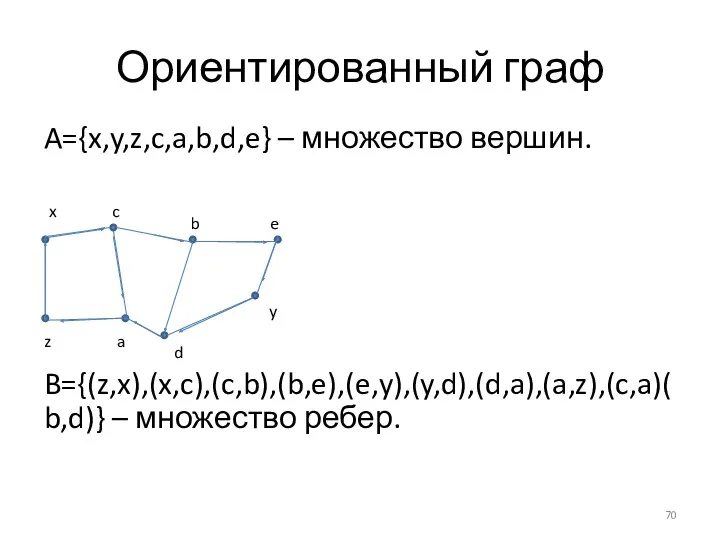
- 66. Ориентированный граф. A={x,y,z,c,a,b,d,e} – множество вершин. B={(z,x),(x,c),(c,b),(b,e),(e,y),(y,d),(d,a),(a,z),(c,a)(b,d)} – множество ребер.
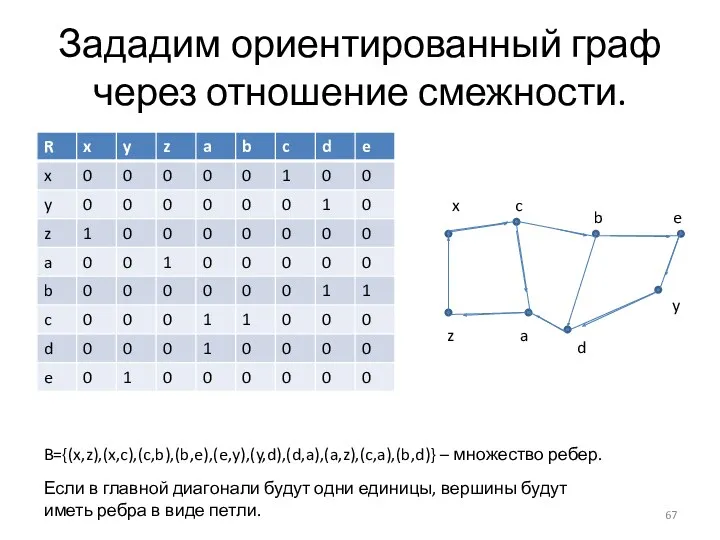
- 67. Зададим ориентированный граф через отношение смежности. B={(x,z),(x,c),(c,b),(b,e),(e,y),(y,d),(d,a),(a,z),(c,a),(b,d)} – множество ребер. Если в главной диагонали будут одни
- 68. Неориентированный граф. Можем задать через отношение инцидентности. A={x,y,z,c,a,b,d,e} – множество вершин. B={{x,z},{x,c},{c,b},{b,e},{e,y},{y,d},{d,a},{a,z},{c,a}} – множество ребер.
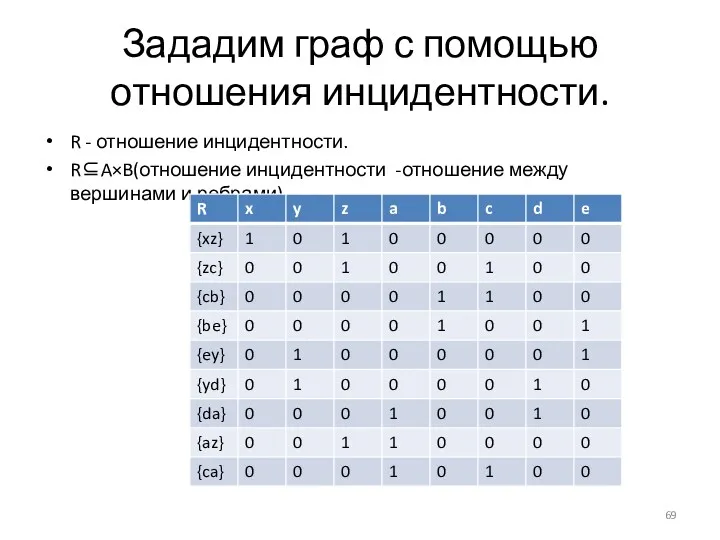
- 69. Зададим граф с помощью отношения инцидентности. R - отношение инцидентности. R⊆A×B(отношение инцидентности -отношение между вершинами и
- 70. Ориентированный граф A={x,y,z,c,a,b,d,e} – множество вершин. B={(z,x),(x,c),(c,b),(b,e),(e,y),(y,d),(d,a),(a,z),(c,a)(b,d)} – множество ребер.
- 71. Зададим орграф через отношение инцидентности.
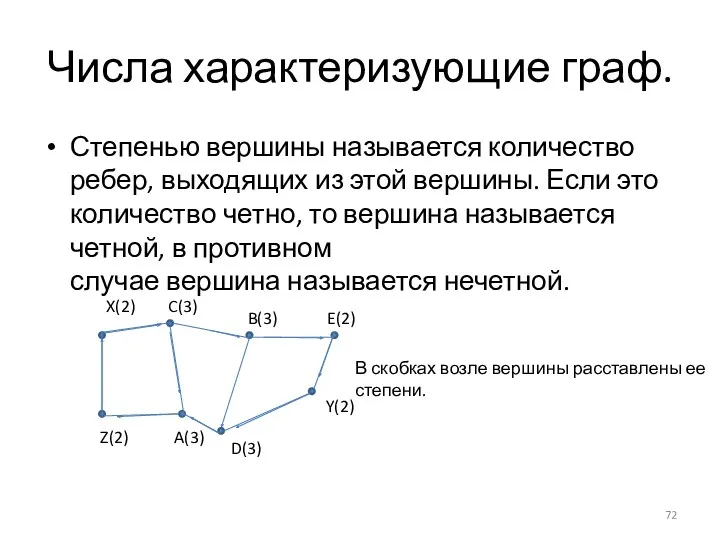
- 72. Числа характеризующие граф. Степенью вершины называется количество ребер, выходящих из этой вершины. Если это количество четно,
- 73. Теорема о степенях вершин в теории графов. Сумма степеней всех вершин графа равна удвоенному количеству всех
- 74. Цикломатическое число. Цикломатическим числом графа - называется число u=N-n+p, где N- число ребер графа, n –
- 75. Найдем путь орг. графа (x,c,b,e,y,d,a,z,x) (x,c,a,z,x) (x,c,b,d,a,z,x)
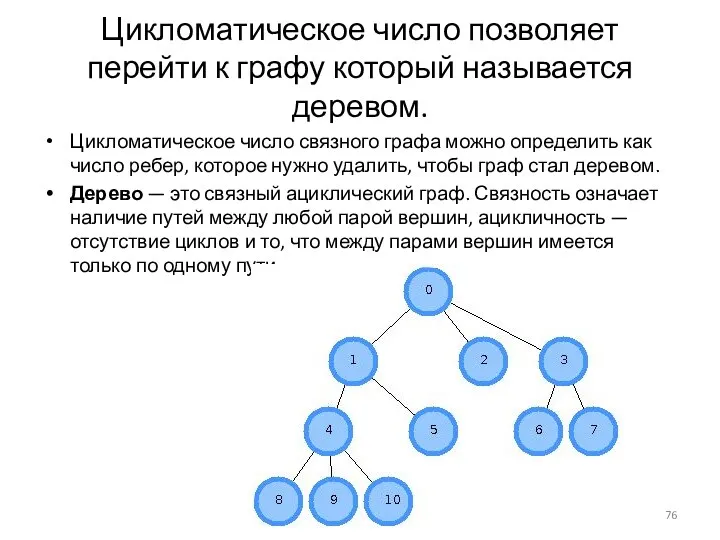
- 76. Цикломатическое число позволяет перейти к графу который называется деревом. Цикломатическое число связного графа можно определить как
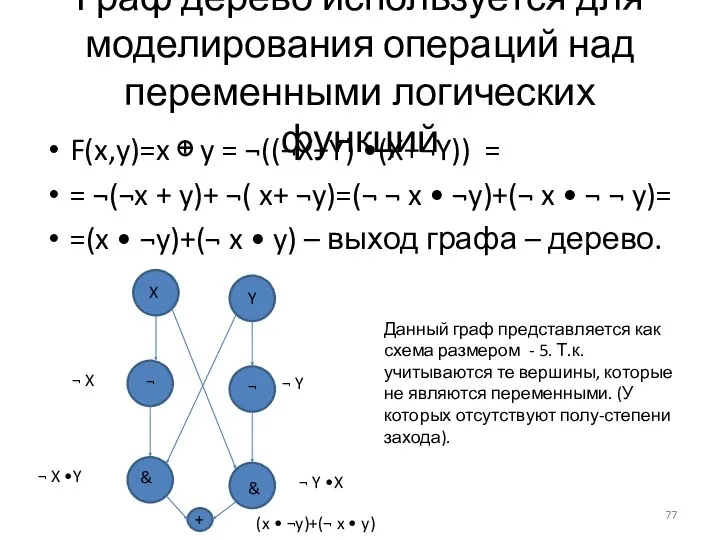
- 77. Граф дерево используется для моделирования операций над переменными логических функций F(x,y)=x ⊕ y = ¬((¬X+Y) •(X+¬Y))
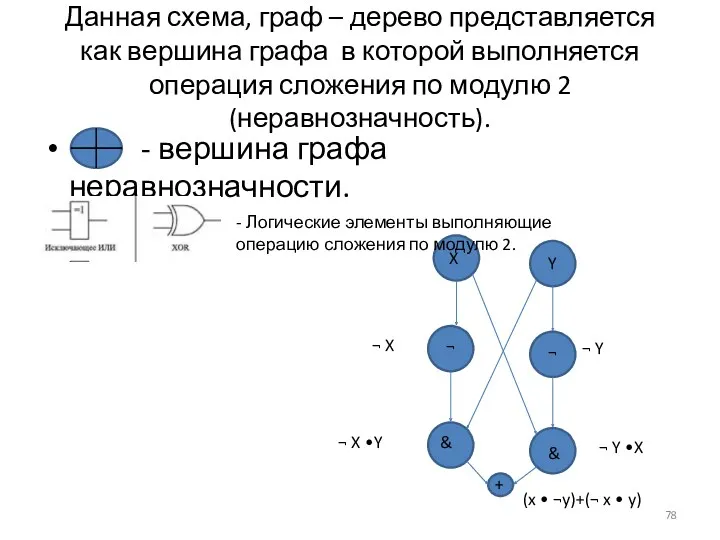
- 78. Данная схема, граф – дерево представляется как вершина графа в которой выполняется операция сложения по модулю
- 79. Рассмотрим функцию сложения по модулю 2. f:An→B A – область определения функции B - область значений
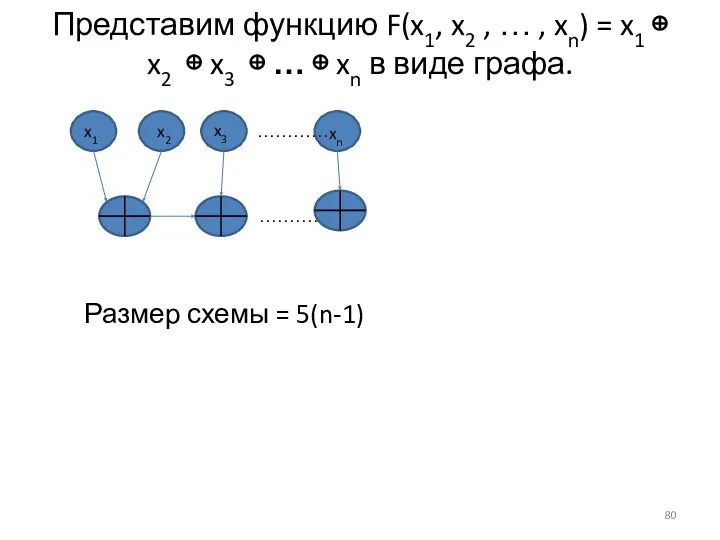
- 80. Представим функцию F(x1, x2 , … , xn) = x1 ⊕ x2 ⊕ x3 ⊕ …
- 82. Скачать презентацию






































 Математика. 1 класс. Урок 75. Длина. Дециметр - Презентация
Математика. 1 класс. Урок 75. Длина. Дециметр - Презентация Меньше или больше. Демонстрационный материал. 5 класс
Меньше или больше. Демонстрационный материал. 5 класс Вписанные и центральные углы
Вписанные и центральные углы Линейная функция и ее график. 7 класс
Линейная функция и ее график. 7 класс Мода и медиана
Мода и медиана Поверхности второго порядка
Поверхности второго порядка Презентация по математике к уроку во 2 классе Замена двузначного числа суммой разрядных слагаемых Школа России
Презентация по математике к уроку во 2 классе Замена двузначного числа суммой разрядных слагаемых Школа России Задачи по планиметрии. ЕГЭ
Задачи по планиметрии. ЕГЭ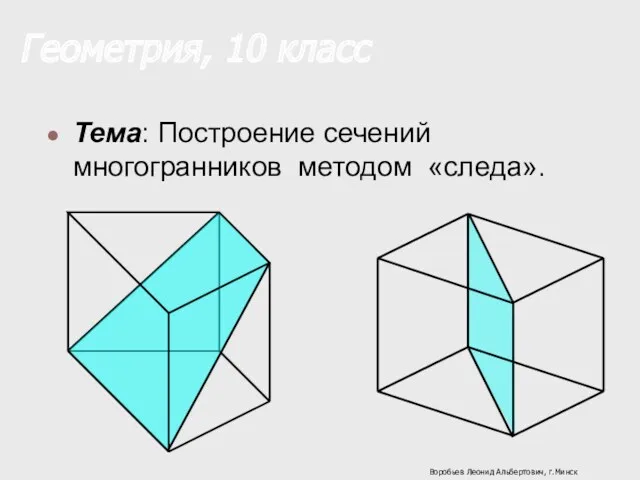 Построение сечений многогранников методом следа
Построение сечений многогранников методом следа Составные задачи. Тренажёр (2 класс)
Составные задачи. Тренажёр (2 класс) Конспект открытого занятия в старшей группе: Интегрированное занятие по математике и развитию речи. Диск
Конспект открытого занятия в старшей группе: Интегрированное занятие по математике и развитию речи. Диск Презентация к уроку математики Повторение 3 класс
Презентация к уроку математики Повторение 3 класс Тренажёр Кот в сапогах (Математика, 1 класс)
Тренажёр Кот в сапогах (Математика, 1 класс) Решение задач с помощью уравнений
Решение задач с помощью уравнений Дифференциальные уравнения с разделяющимися переменными
Дифференциальные уравнения с разделяющимися переменными Формулы сокращенного умножения
Формулы сокращенного умножения Работа с геометрическими фигурами.
Работа с геометрическими фигурами. Параллелепипед. Тетраэдр. Виды многогранников
Параллелепипед. Тетраэдр. Виды многогранников Средства измерений и их классификация. Лекция 7
Средства измерений и их классификация. Лекция 7 Загадки пирамид
Загадки пирамид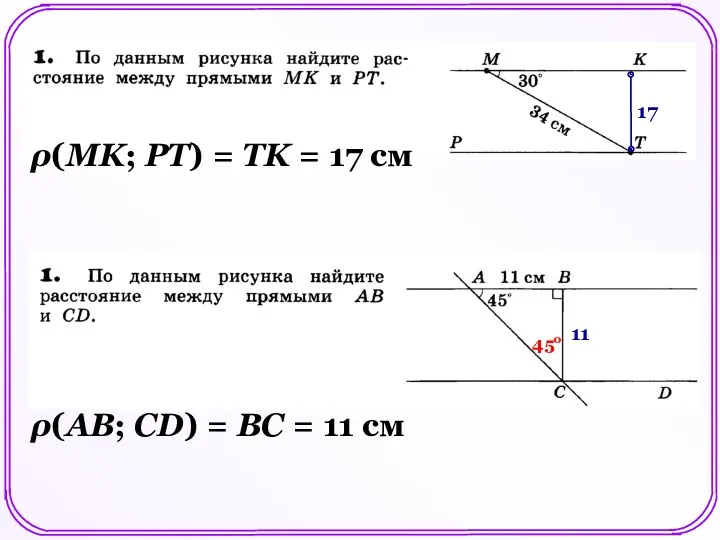 Построение треугольника по трём элементам
Построение треугольника по трём элементам Метрология. Научные изыскания в области метрологии
Метрология. Научные изыскания в области метрологии Полигон и гистограмма. Эмпирическая функция распределения
Полигон и гистограмма. Эмпирическая функция распределения Презентация Состав 6 1 класс УМК Гармония
Презентация Состав 6 1 класс УМК Гармония Статистическое изучение динамики социально-экономических явлений
Статистическое изучение динамики социально-экономических явлений Задачи на движение по реке. Математические модели (9 класс)
Задачи на движение по реке. Математические модели (9 класс) Сложение и вычитание вида 10 + 7, 17 – 7, 17 – 10
Сложение и вычитание вида 10 + 7, 17 – 7, 17 – 10 Единицы массы: тонна и центнер
Единицы массы: тонна и центнер