Содержание
- 2. Гетероскедастичность Одной из предпосылок применения метода наименьших квадратов являлось требование гомоскедастичности, предполагающей независимость случайной составляющей модели
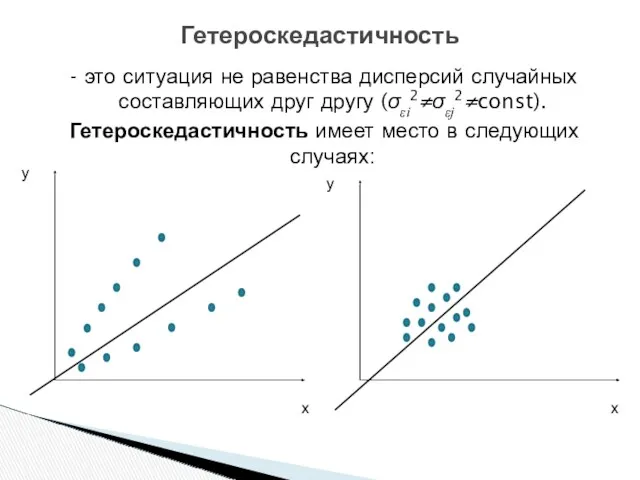
- 3. Гетероскедастичность - это ситуация не равенства дисперсий случайных составляющих друг другу (σεi2≠σεj2≠const). Гетероскедастичность имеет место в
- 4. Последствия гетероскедастичности Неэффективность оценок параметров регрессии; Неточность стандартных ошибок параметров регрессии (следовательно, неверная интерпретация значимости параметров
- 5. Обнаружение гетероскедастичности Осуществляется по тесту Голдфелда–Квандта, который применяется в случае, когда среднее квадратическое отклонение случайной составляющей
- 6. Процедура Голдфелда–Квандта Расчет отношения сумм квадратов отклонений или , при этом в числителе должна быть наибольшая
- 7. Устранение гетероскедастичности Возможно при помощи деления всего уравнения регрессии на величину σεi и замены переменных на
- 8. Эконометрика АВТОКОРРЕЛЯЦИЯ СЛУЧАЙНЫХ СОСТАВЛЯЮЩИХ
- 9. Автокорреляция - это корреляционная зависимость между текущими уровнями каждой переменной и уровнями этой же переменной, сдвинутыми
- 10. Автокорреляция Автокорреляция может быть как положительной, так и отрицательной. Положительная автокорреляция означает постоянное однонаправленное действие неучтенных
- 11. Последствия автокорреляции Неэффективность коэффициентов регрессии (при наличии несмещенности и состоятельности); Занижение стандартных ошибок коэффициентов регрессии.
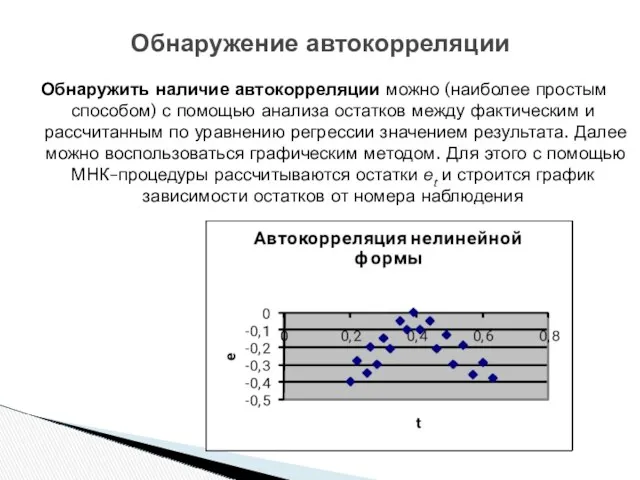
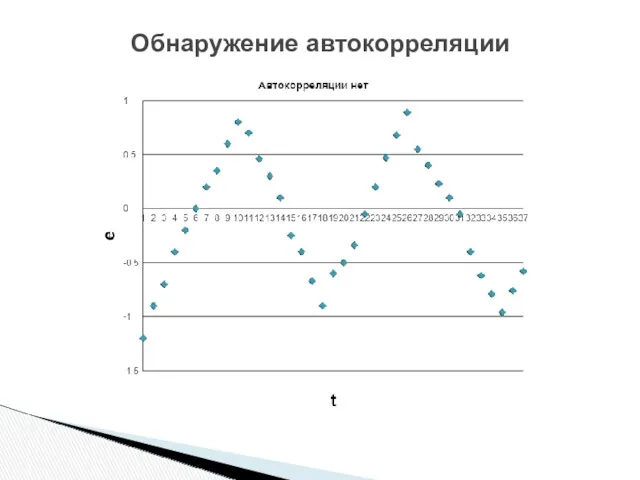
- 12. Обнаружение автокорреляции Обнаружить наличие автокорреляции можно (наиболее простым способом) с помощью анализа остатков между фактическим и
- 13. Обнаружение автокорреляции
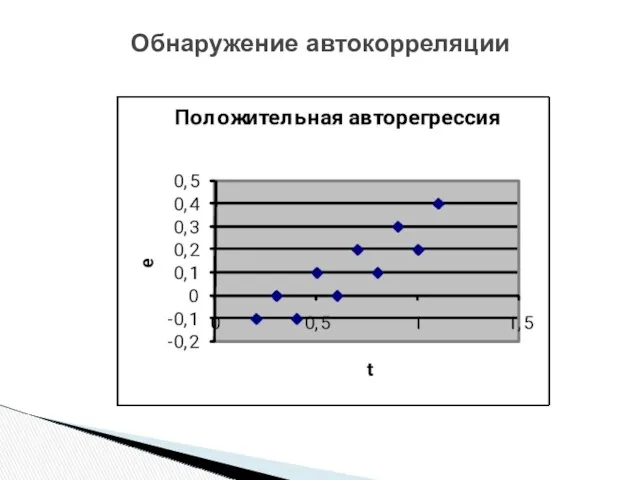
- 14. Обнаружение автокорреляции
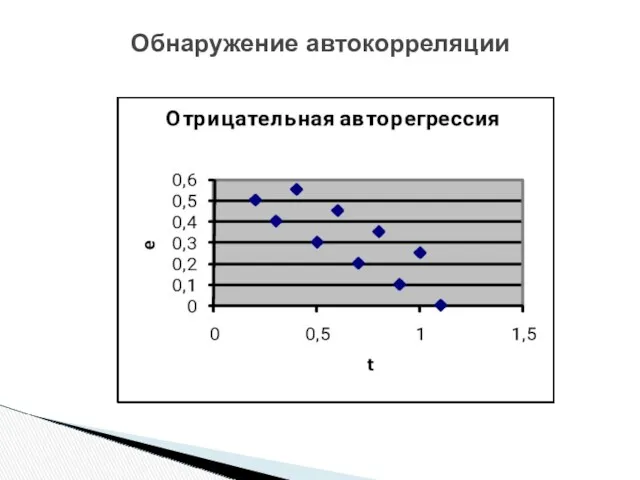
- 15. Обнаружение автокорреляции
- 16. Устранение автокорреляции Необходимо: Выделить фактор, ответственный за автокорреляцию и включить его в уравнение регрессии (но это
- 17. Устранение автокорреляции Произвести преобразование координат уравнения регрессии. В случае парной линейной регрессии уравнение в новых переменных
- 18. Эконометрика АВТОКОРРЕЛЯЦИЯ УРОВНЕЙ ВРЕМЕННОГО РЯДА
- 19. Автокорреляция уровней временного ряда Модели, построенные по временным данным, называются моделями временных рядов – это ряды
- 20. Автокорреляция уровней временного ряда Уровень ряда можно представить в виде функции X=f(T,K,S,ε). В зависимости от вида
- 21. Коэффициент автокорреляции Первого порядка равен: Второго порядка коэффициент рассчитывается по N и N–2 наблюдениям: Далее рассчитываются
- 22. Эконометрика ПОСТРОЕНИЕ ТРЕНДА ВРЕМЕННОГО РЯДА
- 23. Тренд временного ряда Для выявления основной тенденции (тренда) в уровнях ряда, т. е. выравнивания ряда динамики,
- 24. Метод аналитического выравнивания Данный метод заключается в построении уравнения регрессии, характеризующего зависимость уровней ряда от временной
- 25. Метод аналитического выравнивания Конечными разностями первого порядка являются Второго порядка j-го порядка:
- 26. Метод аналитического выравнивания Если тенденция выражается линейным уравнением, то конечные разности первого порядка постоянны, а разности
- 27. Метод аналитического выравнивания При выборе вида функции следует исходить из объема имеющейся информации. Чем больше параметров
- 28. Эконометрика МОДЕЛИРОВАНИЕ СЕЗОННЫХ И ЦИКЛИЧЕСКИХ КОЛЕБАНИЙ
- 29. Моделирование сезонных и циклических колебаний При моделировании сезонных или циклических колебаний существует несколько классических подходов: Расчет
- 30. Самый простой подход Рассмотрим первый наиболее простой из этих подходов для моделирования сезонных колебаний. Выбор типа
- 31. Индекс сезонности и абсолютное отклонение Перед расчетом сезонных компонент ряд динамики выравнивают (например, с помощью метода
- 32. Эконометрика СИСТЕМЫ ЭКОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
- 33. Системы эконометрических уравнений Сложные социально–экономические явления обычно описываются с помощью целой системы взаимосвязанных эконометрических уравнений. В
- 34. Системы взаимозависимых уравнений Являются наиболее сложными. Для них традиционный МНК не применим, так как нарушаются его
- 36. Скачать презентацию




























 Касательная к окружности
Касательная к окружности Общий приём сложения однозначных чисел с переходом через десяток
Общий приём сложения однозначных чисел с переходом через десяток Начальные геометрические сведения. (7 класс)
Начальные геометрические сведения. (7 класс) Математический бой. Урок–игра в 6 классе
Математический бой. Урок–игра в 6 классе Теорема синусов и косинусов
Теорема синусов и косинусов Презентация к уроку математика Табличное вычитание вида 15-7
Презентация к уроку математика Табличное вычитание вида 15-7 Разложение многочленов на множители с помощью комбинирования различных приёмов. Класс: 7
Разложение многочленов на множители с помощью комбинирования различных приёмов. Класс: 7 Увлекательная математика
Увлекательная математика Делимость чисел
Делимость чисел Деление на двузначное число
Деление на двузначное число Решение тригонометрических уравнений и способы отбора корней на заданном промежутке
Решение тригонометрических уравнений и способы отбора корней на заданном промежутке Алгебраический метод решения логических задач
Алгебраический метод решения логических задач Степень числа. 7 класс
Степень числа. 7 класс Задачи ОГЭ и ЕГЭ по геометрии
Задачи ОГЭ и ЕГЭ по геометрии Численными методы решения инженерных задач
Численными методы решения инженерных задач Множества. Понятие множества
Множества. Понятие множества презентация по математике на тему Ось симметрии
презентация по математике на тему Ось симметрии Среднее арифметическое нескольких чисел
Среднее арифметическое нескольких чисел Қозғалыс жылдамдығы. Жылдамдықтың өлшем бірліктері
Қозғалыс жылдамдығы. Жылдамдықтың өлшем бірліктері Властивості тригонометричних функцій. Алгебра. 10 клас
Властивості тригонометричних функцій. Алгебра. 10 клас Многоугольники. Примеры многоугольников
Многоугольники. Примеры многоугольников Тестовый контроль знаний, как основа диагностики качества обучения
Тестовый контроль знаний, как основа диагностики качества обучения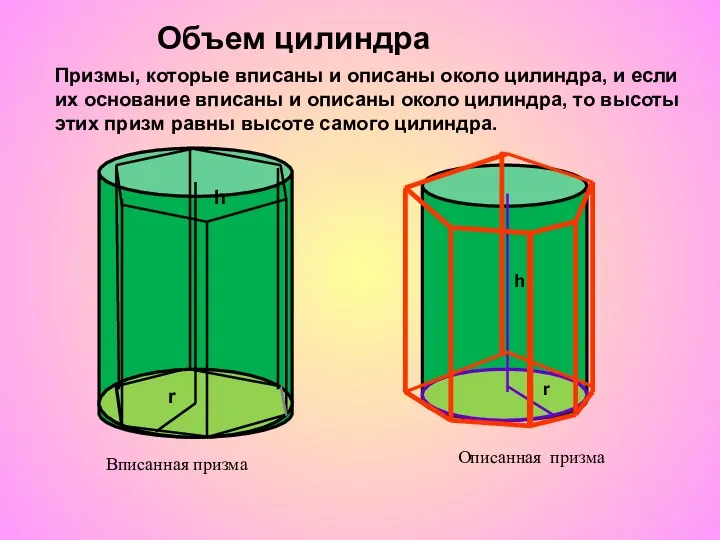 Объем цилиндра
Объем цилиндра Величины. Классная работа
Величины. Классная работа Случаи вычитания 17 - 18 -
Случаи вычитания 17 - 18 - Числовые и буквенные выражения
Числовые и буквенные выражения Проценты. Как найти число по его проценту
Проценты. Как найти число по его проценту Презентация к уроку математики для 3 класса Деление суммы на число
Презентация к уроку математики для 3 класса Деление суммы на число