Содержание
- 2. Отношение делимости и его свойства
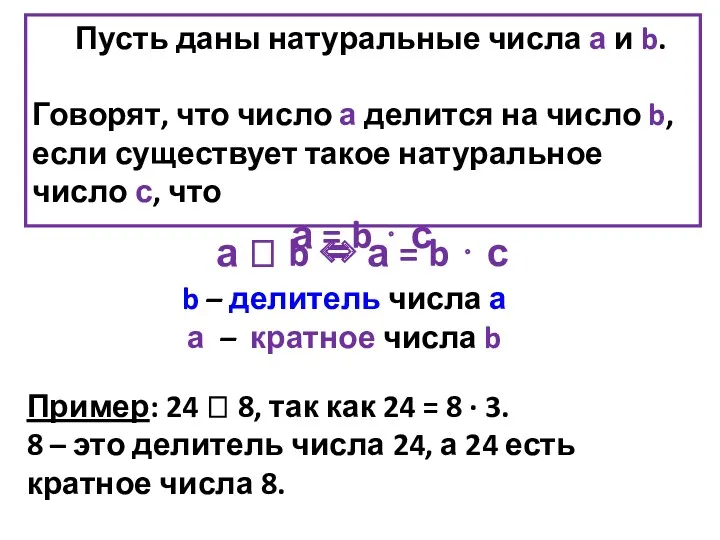
- 3. Пусть даны натуральные числа а и b. Говорят, что число а делится на число b, если
- 4. Замечание: понятие «делитель данного числа» следует отличать от понятия «делитель», обозначающего то число, на которое делят.
- 5. Свойства отношения делимости 1. Отношение делимости рефлексивно, т. е. любое натуральное число делится само на себя:
- 6. 5. Отношение делимости транзитивно, т.е. а b и b с ⇒ а с
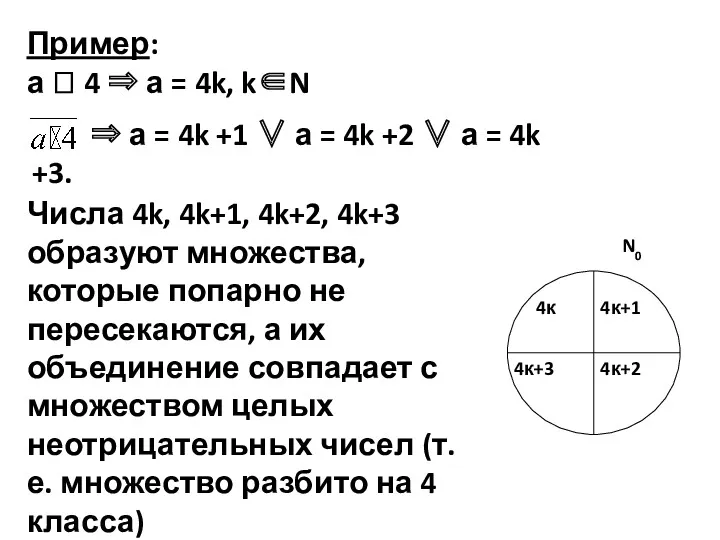
- 7. Пример: а 4 ⇒ а = 4k, k∈N ⇒ а = 4k +1 ∨ а
- 8. Делимость суммы, разности, произведения Теорема 1 (признак делимости суммы) Если числа а и b делятся на
- 9. Теорема 3 (признак делимости разности) Если числа а и b делятся на с и а >
- 10. Теорема 5 (признак делимости произведения) Если число а делится на b, то произведение вида ах, где
- 11. Теорема 7. Если произведение ас делится на произведение bс, причем с – натуральное число, то и
- 12. Упражнения 1. Не выполняя сложения, установите, делится ли значение выражения на 3: а) 180 + 144;
- 13. Признаки делимости
- 14. Признак делимости на число b – это правило, позволяющее по записи числа а узнавать, делится ли
- 15. Признак делимости на 2 Для того чтобы число х делилось на 2, необходимо и достаточно, чтобы
- 16. Признак делимости на 5 Для того чтобы число х делилось на 5, необходимо и достаточно, чтобы
- 17. Признак делимости на 4 Для того чтобы число х делилось на 4, необходимо и достаточно, чтобы
- 18. Признак делимости на 25 Для того чтобы число х делилось на 25, необходимо и достаточно, чтобы
- 19. Признак делимости на 8 Для того чтобы число х делилось на 8, необходимо и достаточно, чтобы
- 20. Признак делимости на 9 Для того чтобы число х делилось на 9, необходимо и достаточно, чтобы
- 21. х = аn·(99..9+1) + аn-1·(99…9+1) + … + а1·(9+1) + а0 х = аn·99..9 + аn-1·99…9
- 22. Признак делимости на 7 Число х делится на 7 тогда и только тогда, когда на 7
- 23. Признак делимости на 11 Число х делится на 11 тогда и только тогда, когда на 11
- 24. Признак делимости на 13 Число х делится на 13 тогда и только тогда, когда на 13
- 25. Общий признак делимости на 7 и 13 Число х делится на 7(13) тогда и только тогда,
- 27. Скачать презентацию






















 Случаи сложения вида +8, +9
Случаи сложения вида +8, +9 Формула корней квадратного уравнения
Формула корней квадратного уравнения Длина окружности и площадь круга
Длина окружности и площадь круга Множества. Элементы множества
Множества. Элементы множества Письмове множення багатоцифрових чисел на одноцифрове число
Письмове множення багатоцифрових чисел на одноцифрове число Решение задач с помощью систем уравнений (6)
Решение задач с помощью систем уравнений (6) Влияние формы предмета на представление о его характере
Влияние формы предмета на представление о его характере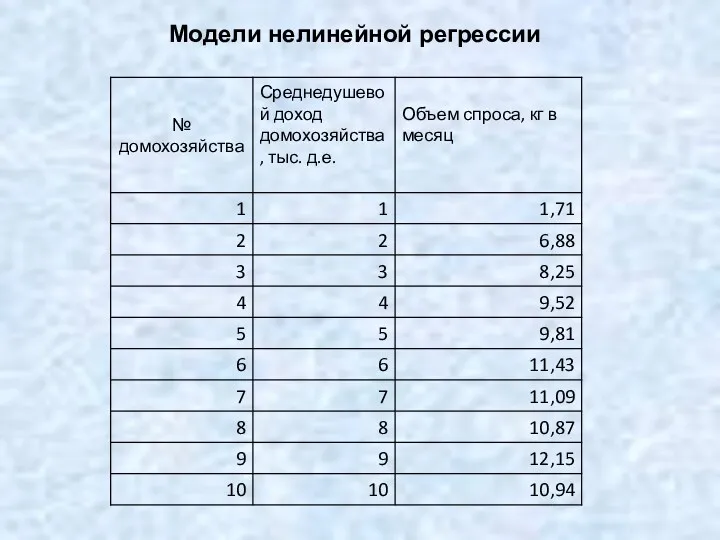 Модель парной нелинейной регрессии
Модель парной нелинейной регрессии Замечательные точки треугольника. Теорема о серединном перпендикуляре. 8 класс
Замечательные точки треугольника. Теорема о серединном перпендикуляре. 8 класс Численные методы решения уравнения
Численные методы решения уравнения Общие вопросы изучения нумерации
Общие вопросы изучения нумерации Понятие арифметического квадратного корня
Понятие арифметического квадратного корня Начертательная геометрия. Поверхности. (Лекция 4)
Начертательная геометрия. Поверхности. (Лекция 4) Расстояние между параллельными прямыми
Расстояние между параллельными прямыми Повторение. Обыкновенные дроби
Повторение. Обыкновенные дроби Умножение положительных и отрицательных чисел
Умножение положительных и отрицательных чисел Функция и ее график
Функция и ее график Площа трикутника
Площа трикутника Численные методы линейной алгебры. Примеры выполнения заданий в Mathcad
Численные методы линейной алгебры. Примеры выполнения заданий в Mathcad Умножение и деление положительных и отрицательных чисел
Умножение и деление положительных и отрицательных чисел Теорема Безу. Схема Горнера. 10 класс
Теорема Безу. Схема Горнера. 10 класс Системы линейных неравенств с одной переменной. 9 класс
Системы линейных неравенств с одной переменной. 9 класс Статистические методы анализа связей
Статистические методы анализа связей Презентация к уроку Величины
Презентация к уроку Величины Признаки делимости на 10, на 5 и на 2
Признаки делимости на 10, на 5 и на 2 Умножение и деление степеней
Умножение и деление степеней Математика. 1 класс. Урок 44. Числа 1-7 - Презентация
Математика. 1 класс. Урок 44. Числа 1-7 - Презентация Основные теоремы и формулы теории вероятности
Основные теоремы и формулы теории вероятности